Time Fractals in Golden Ratio Proportions and TCL demo example calculator, numerical analysis
Time Fractals in Golden Ratio Proportions and TCL demo example calculator, numerical analysis
This page is under development. Comments are welcome, but please load any comments in the comments section at the bottom of the page. Please include your wiki MONIKER and date in your comment with the same courtesy that I will give you. Aside from your courtesy, your wiki MONIKER and date as a signature and minimal good faith of any internet post are the rules of this TCL-WIKI. Its very hard to reply reasonably without some background of the correspondent on his WIKI bio page. Thanks,gold 30Apr2021
- Time Fractals in Golden Ratio Proportions and TCL demo example calculator, numerical analysis
- Introduction
- Golden Ratio Constants
- Example of Joe Blow in the Mills of Time
- Elliot Wave Breakpoints from Fibonacci constants
- Table of Elliot Wave Breakpoints
- Revolution Periods and Distance of Planets from the Sun
- Experimental exchange of affinity pairs in lines 3 and 4 to modify Hexagram with time shift
- Continuing Thread on Hexagram #21
- Speculations on Time Waves
- Figure . Contrast between Results on constant length and variable_length_waves
- Fractal Limits of the simulated reality from Koch snowflake
- Test Suite on Time Fractals in Golden Ratio Proportions
- Pushbutton Operation
- Conclusions
- Pseudocode, Equations, and Wiki Page Checklist
- Testcases Section
- Testcase 1, Test on Human Life Cycles
- Testcase 2, Human Life Cycles
- Testcase 3, Human Teenager Trial
- Testcase 4, Predicted Human Teenager
- Testcase 5a, Successive Fibonacci constants
- Testcase 5b, Stock Markets, Fibonacci constants
- Testcase 6a, life cycle of cicada insect and a separate cicada species
- Testcase 6b, Life cycle of a separate cicada species
- Testcase 7, Puberty at 13 years old
- Testcase 8, Width and Height of DNA Strand
- Testcase 10, Starfish has 5 arms
- Testcase 11, Ratio of male bees to female bees in hive
- Testcase 12, Example of Joe Blow in the Mills of Time
- Testcase 13, Examples of Variable Time Waves Referenced to Calendar Years
- Screenshots Section
- figure 1a. Golden_Ratio_screenshot
- figure 1b. Time_Fractals_in_Golden_Ratio_report_card
- figure 2.time_fractals_equation
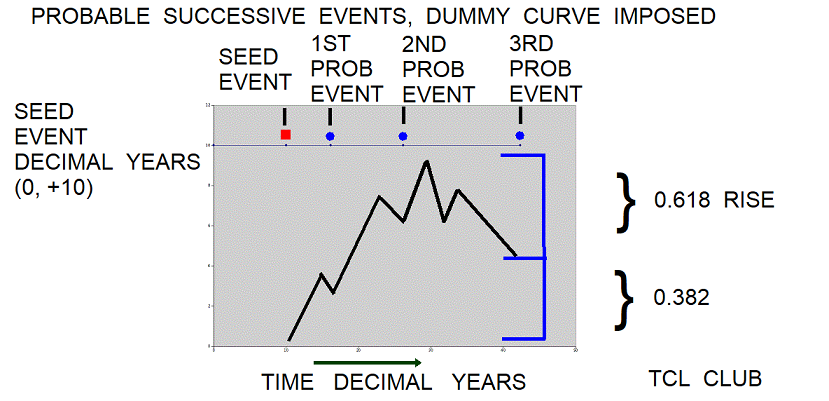
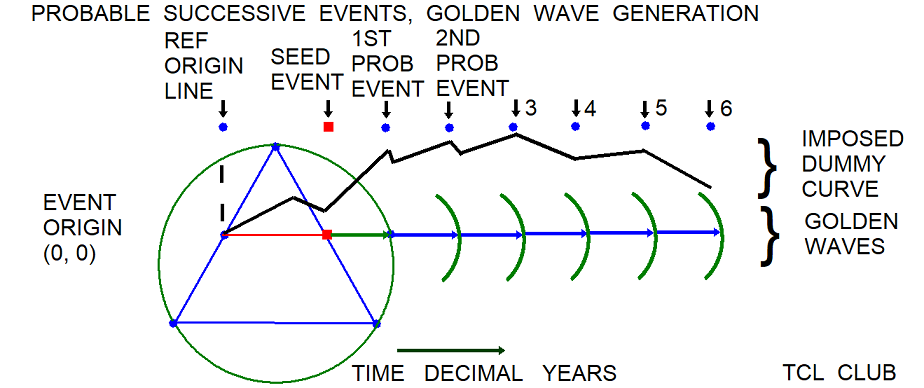
- figure 3.time_fractal_dummy_curve
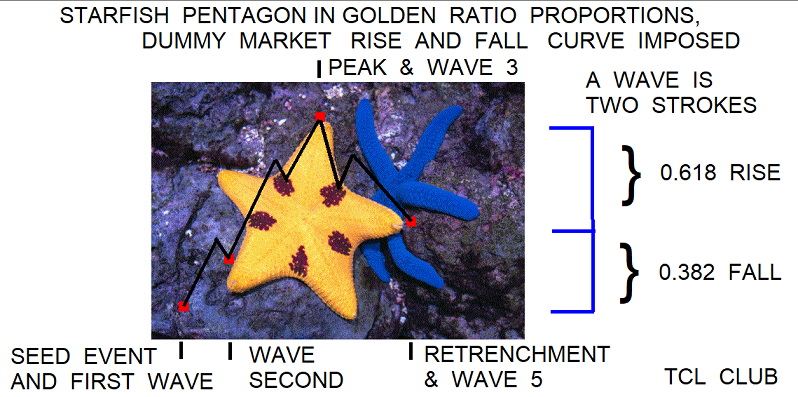
- figure 4. Time_Fractal_Starfish
- figure 5.Golden_Ratio_Proportions
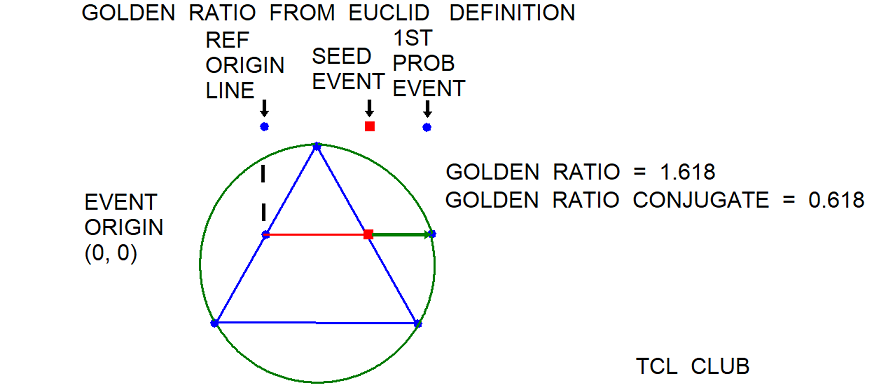
- figure 6.Golden_Ratio_definition
- figure 7. Golden_Ratio_waves
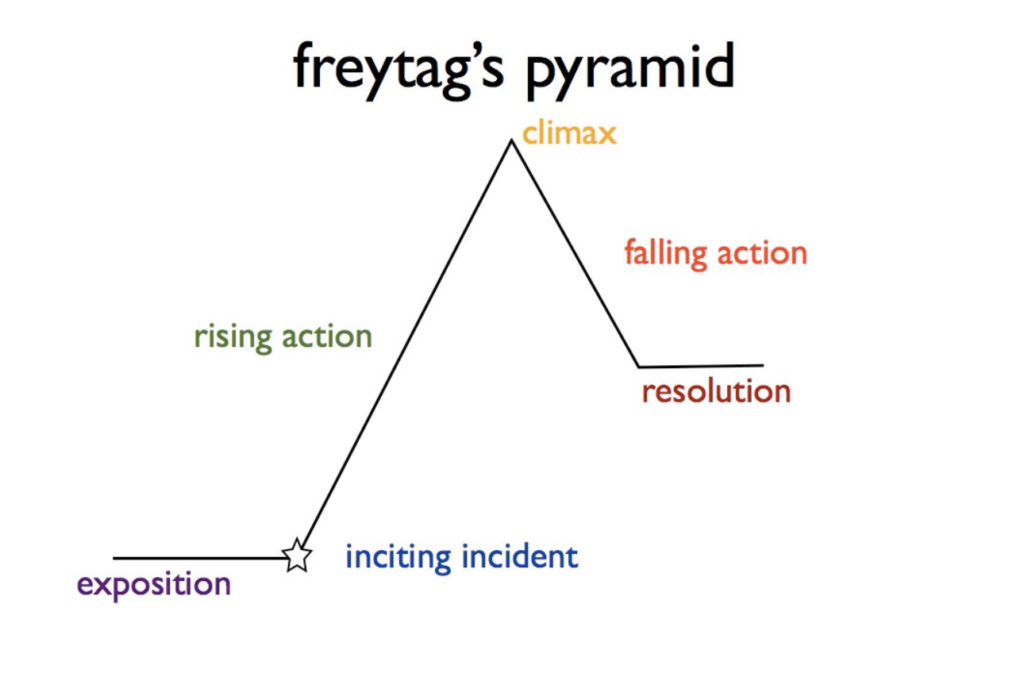
- figure 7b. Proportions Freytag pyramid
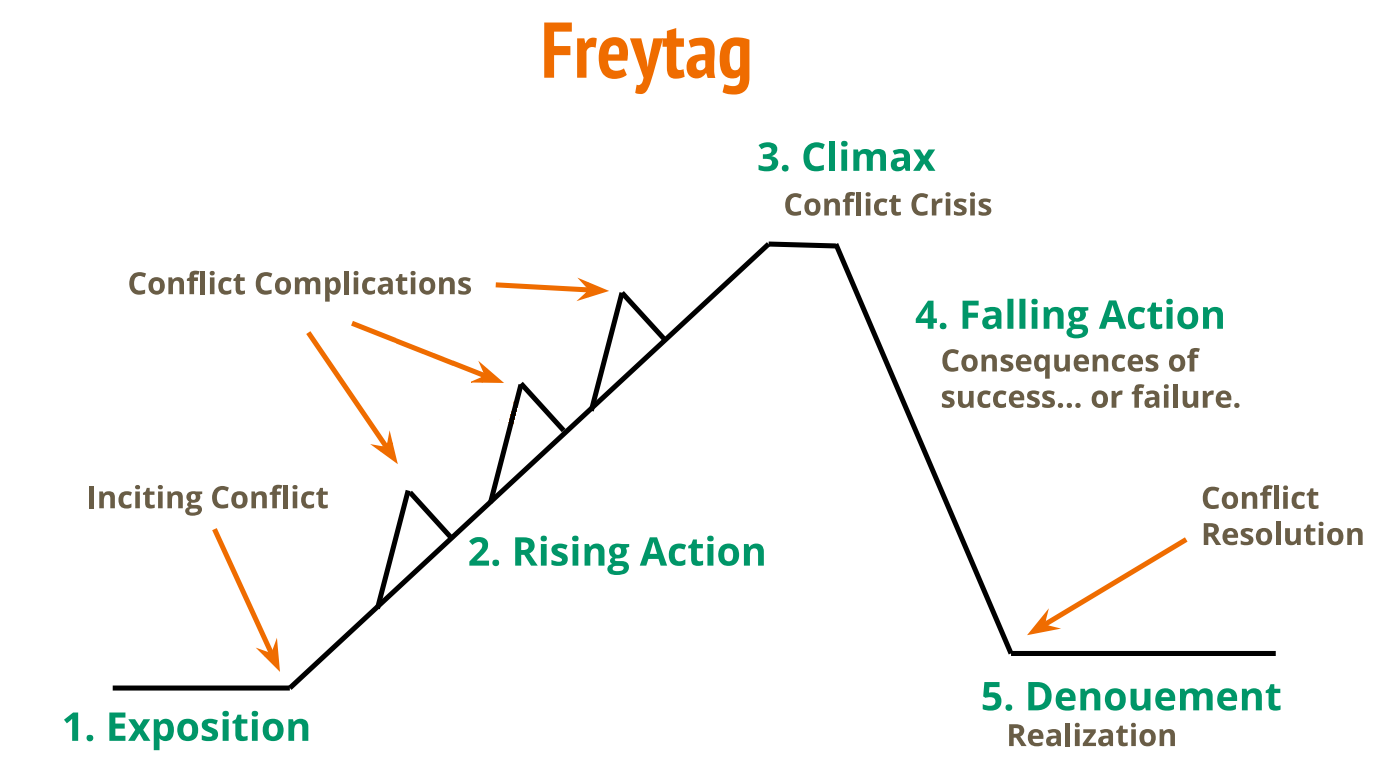
- figure 7c. Proportions Freytag pyramid 2
- figure 7e.Golden_Ratio_waves, simulation in ripple tank
- figure 8.Golden_Ratio_waves_2, simulation in ripple tank
- figure 9. constant_length_waves from Joe Blow example
- figure 10. variable_length_waves from 1941 seed_date example
- figure 11. Cicada studying math
- figure 12. Albert Einstein block Universe
- figure 13. Albert Einstein, John Archibald Wheeler
- figure 14. model using poker chips
- figure 15. Wormhole
- figure 16. Multiple Universes
- References:
- References: Elliott Wave Theory, Stock Markets
- References: Fractal Waves and Fractal Limits
- References: Planets, Titius–Bode law
- References: cicada insects
- Appendix Code
- Hidden Comments Section
Introduction
gold Here are some calculations on time fractal windows. This calculator uses golden ratio proportions to predict successive time windows or successive time fractals of similar probable occurrences based on either a seed time or an initial human age in decimal years. There is plenty of uncertainty about probable occurrences events after the seed time in decimal years. But the probable occurrences are largely based on growth, accumulation, and succession following the golden ratio proportions. Not all events in time have golden ratio proportions.
Golden Ratio Constants
The golden ratio constant is 1.6180339887… As used in the TCL program, the golden ratio conjugate is 0.6180339887… In some Bitcoin circles, a peak is considered 1.6X and a dip is considered 0.6X. The most commonly used Fibonacci ratios as dips include the 23.6%, 38.2%, 50%, 61.8%, and 78.6% shorts. A version of 61.8% is loaded in the TCL program as the factor 0.618... Not sure these Fibonacci ratios apply on all occasions, but there is considerable interest in predicting peaks and dips in Bitcoin cryptocurrency.
#; derivation of analyst Fibonacci constants
set g_constant1 1.61803398874989484820
set result [ expr { 1./ ($g_constant1 * $g_constant1 ) }]
#; result out = 2.6180339887498945
set g_constant2 1.61803398874989484820
expr { 1./ ($g_constant2 * $g_constant2 ) }
#; result out = 0.38196601125010515The golden time point in any duration is defined 61.8% in its entire length of time. Golden time segments may defined as multiple and alternating time segments in proportion to Fibonacci series constants. An example is 3:2:5:2 (here, 4 time segments approximating golden ratio equivalence 1.618:1:1.618:1). The reported testcase is roughly 3:2:2:5.
Initial Human Testcases
Most agree that humans start puberty at 13 years old and become mature at 21 years. Enter 13 years for puberty in calculator and receive rounded 21 years for human maturity. The hand calculation was '''expr { (13.) * (1.618/1.) }
;# returns 21.0 years rounded'''. Refer to '''Testcases 1,2,3,4, & 7'''.
Width and Height of DNA Strand
Most of the golden ratio problems I can find deal with dimensions rather than time. According to Gregg Braden in the book Fractal Time , one complete turn of a DNA strand is 34 angstrom units in length and 21 angstrom units wide. Enter 21 angstrom units for DNA width in TCL calculator and receive rounded 34 angstrom units for DNA height. Refer to Testcase 8.
Perhaps an algorithm for the reverse progress would be useful, Height >> Width. The TCL expression would be expr { 34. * ( 1/ 1.618 ) } or 21.013 angstrom units width.
Life cycle of cicada insect and separate cicada species, genus Magicicada in USA
The cicada insect in the USA has a life cycle of 17 years, believed to be based loosely based on the solar cycle of eleven years. Enter 10 decimal years in the TCL calculator, result rounds down to 17 years. The cicada insects emerge in May of the seventeenth year, so the hand TCL expression was expr { 17 + 5./12 } as 17.4166 or rounded 17.4 decimal years. Comment that time coincidence is not proof of causation. Refer to testcase 6a and figure 8.
Another cicada insect species in the USA has a life cycle of 13 years, possibly an unknown factor may be involved. From the Elliot wave theory, there are other Fibonacci constants for breakpoints. Skipping a number in the Fibonacci sequence (55/144 and 144/55) produces 2 more Fibonacci breakpoint constants, 38.2 percent and 261.8%. In this case the Fibonacci break constant 38.2% is of interest, so the hand TCL expression was expr { 10. * ( 1. + 100.* 38.2% ) } as expr { 10. *1.382 } to 13.819 or rounded 13.8 decimal years. In this problem, we used reverse logic or the reverse golden ratio proc. What number of years would return a life cycle of 13 years? So the hand TCL expression was expr { $age_years * (1./1.618) } as or rounded 8 decimal years. Refer to testcase 6b.
Stephen Jay Gould in the book, Ever Since Darwin, reported that possible carnivorous insect predators with life cycle of < 2, 3, 4, & 5 > years might have difficulty with joint and coincident emergence with the 13 and 17 year life cycles of cicada, genus Magicicada. Gould related that 13-year and 17-year life cycles cannot be tracked by any smaller number. In further elaboration, insect predators with life cycle of < 2, 3, 4, & 5 > years could not break the larger prime number keys of the 13-year and 17-year life cycles. A predator insect with a life cycle of 5 years might have to wait for the 17 year cicada insect for the product expr { 5. * 17. }, 85 years. A predator insect with a life cycle of 5 years might have to wait for the 13 year cicada insect for the product expr { 5. * 17. }, 65 years. The life cycles of the 13 and 17 year cicada coincide in the product expr { 13. * 17. }, 221 years. A predator insect with a life cycle of 5 years might have to wait for the joint appearance year of 13 and 17 year cicada insect for the product expr { 5. * 221. }, 1105 years. However, the territories of 13 and 17 year cicada insects generally do not perfectly overlap plus the emergence year may differ of be off key or of the time cycle.
Note. Sweet number between N and 2N. As rule of thumb, a mathematician reported that Sweet number defined as RND {(1-e)*N)}. However, (1 plus phi conjugate) or RND {(1.6180339887 * N)} would give equivalent answer in small number field, less than 10.
Example of Joe Blow in the Mills of Time
Lets suppose Joe Blow (not real name) was born on 4Jul1980 (julian day 185) , had seed year event of parents divorce on 15Sep1993 (julian 258), and graduated with BA on 15Jun2003 (julian 166). At time of parents divorce and in mortal recollection, Joe’s human age at the seed year is estimated at expr { 1993 + 256/364. - (1980+185/364.) }, 13.195 years. Joe’s reference year would be birth day as expr { 1980 + julian_date / days_in_year }, expr { 1980 + 185. / 364.}, rnd 1980.508 CE. One may load the seed year as 13.195 years and reference birthday in Georgian years as 1980.508 years. The calculator will generate a series of time waves or time cycles based on the golden ratio. For the case of Joe Blow, the estimated golden_time_cycle was rounded 8.155 years.The hand calculation was expr { (13.195) * (1./1.618) } ;# returns 8.155 years rounded. The set of results in years of age was <list 0.0000 13.195 21.350 29.505 37.660 45.815 53.970 62.125>. The TCL program also rescaled the results in Georgian years also, < list 1980.5 1993.7 2001.9 2010.0 2018.2 2026.3 2034.5 2042.6 >. Refer to Testcase 12 with charts 6 & 7.
Simultaneous sets of Golden Waves are possible in a person's lifetime. For the case of Joe Blow, simultaneous sets of Golden Waves were gamed at 13 and 16 years of age. Subject to interpretation, a major event at 45 years of age was coincident to both sets of Golden Waves.
The studies on human life cycles and passages offer some validation to the time wave theory. Whether numerical coincidence or not, many authors suggest a possible subcycle of 7-8 years and a subcycle of 10-11 years in human affairs. Most agree that humans start puberty at 13 years old and become mature at 21 years. Enter 13 years for puberty in calculator and receive rounded 21 years for human maturity. The male is considered adult at age 21. Magazine reports that average marriage has lasted 7 years over past 50 years. Women get married at average age 27.8 years. Men get married at the average age of 29.8 years. With the givens, the average age of divorce for the male was expr { 29.8 + 7. }, 36.8 years of age. Based on independent sources, college educated employees with Bachelor's degrees tend to make the most money in their 50s, but possible sharp declines may expected after 60 years of age. Average retirement age is 65 for men and 63 for women. Mortality was set at 73 years of age. Sequence numbers from real life apply. The list of street_life_male_avg in human age years was < list 0.0 13. 18. 21. 24. 29.8 36.8 43.5 55. 60. 65. 73. >. The list of street_life_male_avg was loaded into the program deck for ready comparison with the calculated results in years of age and rescaled in Georgian years also.
;# pseudocode, Equations, and Joe Blow Checklist ***
set birth_year 1980.508
set seed year 13.195
set Grade_School 6
set Middle_School 2
set High_School 4
set College 4
set Graduate_School 2
set values [list 6 8 12 16 18]
set street_life_male_avg [ list 0.0 13. 18. 21. 24. 29.8 36.8 43.5 55. 60. 65. 73.] ;# in human age yearsStarfish has 5 arms.
The starfish has 5 arms and the dimensions of a pentagon in length, rather than time units. Enter 1 inch for width between two arms in TCL calculator and receive rounded 1.816 inchs for maximum width or length across two alternate arms. The hand calculation was expr { (1.) * (1.618/1.) } #; returns 1.618. The units cancel out in the calculator, so one may enter 8 centimeters and receive proportional 12.9 centimeters across 2 opposing arms, using proportional calculations with the golden mean. The hand calculation was ''' expr { (8.) * (1.618/1.) } ;# returns 12.9 centimeters rounded. Refer to Testcase 10.
Successive Fibonacci constants
This is not intended use of calculator, but the calculator can generate Successive Fibonacci sequence numbers as reals. If the entry is a Fibonacci number greater than two (2), the TCL calculator should approximate the next successive Fibonacci numbers as approximate reals, but need to round to nearest integer. The On-Line Encyclopedia of Integer Sequences A000045 gives the Fibonacci numbers as follows 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, 28657, 46368, 75025, 121393, 196418, 317811, 514229, 832040, 1346269. Refer to Testcase 5a.
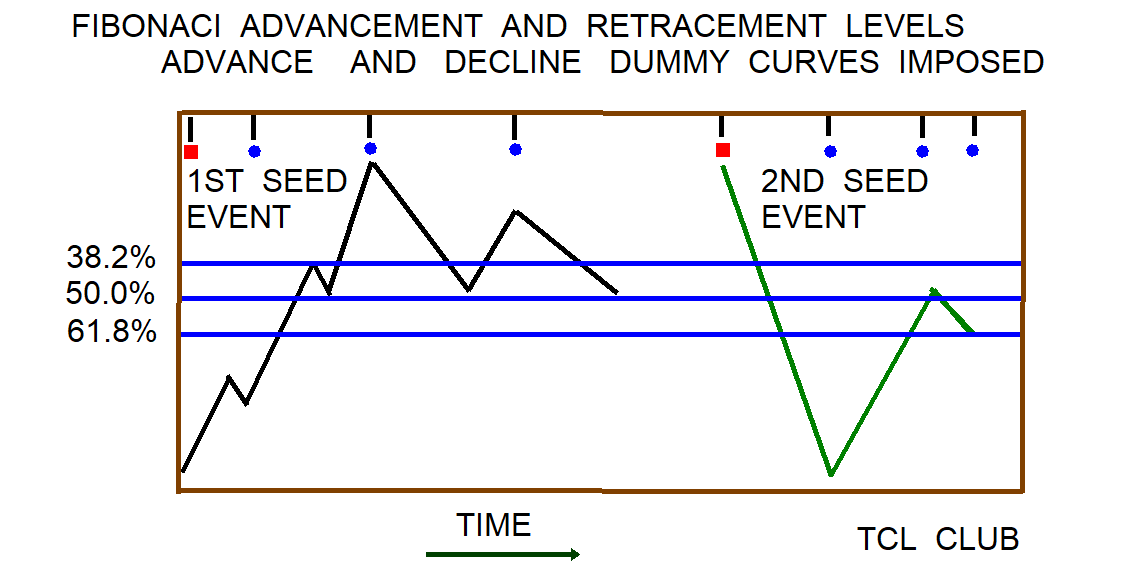
Elliot Wave Breakpoints from Fibonacci constants
The Elliot wave analyst Fibonacci constants : 161.8%.,61.8%, 38.2%, 23.6%, and 50.0% are apparently derived from OEIS A000045 Fibonacci series, <3,5,8>. An Elliot wave is defined as two strokes, up and down. For example, an Elliot wave might have a rise (factor) of 0.618 and a fall (factor) of 0.382, where the initial position point or reference point is scaled and normalized to unity (1). If the calculator entry is a Fibonacci number greater than two (2), the TCL calculator should approximate the next successive Fibonacci numbers as reals, but need to round to nearest integer. The On-Line Encyclopedia of Integer Sequences A000045 gives the Fibonacci numbers as follows 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, 28657, 46368, 75025, 121393, 196418, 317811, 514229, 832040, 1346269.
An interesting set of fractions for Elliot Wave Breakpoints may be developed by dividing 5 by the Integer Sequence A000045 after 3. These fractions approximate and track the powers of the golden ratio conjugate $grc**N fairly well. An example for the Elliot wave 4, < expr {5./13} = 0.38461538461539 > approximates < { $grc**2} = 0.3819660112501052 > . Another example for the Elliot wave 5 was < expr {5./21. } = 0.23809523809523808 > approximates < expr { $grc**3} = 0.23606797749978975 >. Another example was < expr {5./34. } = 0.14705882352941177 > approximates < expr { $grc**4}= 0.14589803375031551 >.
Elliot wave analysis is a popular technical analysis approach used in the stock market and other financial markets. This method is based on the idea that the market moves in cycles, and these cycles can be divided into smaller waves or patterns. The Fibonacci numbers, which are derived from the Fibonacci sequence, are used in this analysis to identify support and resistance levels, as well as potential targets for price movements. The Elliot wave constants and fractions approximate the powers of the golden ratio conjugate, which is a mathematical concept that describes the relationship between consecutive numbers in the Fibonacci sequence. By using these fractions as breakpoints, traders can identify potential turning points in the market and make better-informed trading decisions. Overall, Elliot wave analysis and the use of Fibonacci numbers and the golden ratio conjugate can provide valuable insights for traders and investors looking to understand and predict market trends.
;# Use one line errorx proc to estimate percent errors in approximate Elliot Wave Breakpoints
proc errorx {aa bb} {expr { $aa > $bb ? (($aa*1.)/$bb -1.)*100. : (($bb*1.)/$aa -1.)*100.}}
set grc 1.61803398874989484820 ;# golden ratio constant
set grc .61803398874989484820 ;# golden ratio conjugate
set wave_1a [ expr { 5./8. } ] ;# returns 0.625, very rough approximate $grc
set wave_2a [ expr { 8./5. } ] ;# returns 1.6, very rough approximate $gr
set wave_3a [ { 832040./ 1346269.} ] ;# returns 0.6180339887496481
set error_1 [ $grc [/ 5. 8. ] ;# returns 1.127 percent error on very rough approximate $grc
set error_2 [ $grc [/ 987. 1597. ] ;# returns 2.837e-5 percent error
set error_3 [ $grc [/ 832040. 1346269. ] ;# returns 3.992e-11 percent errorTable of Elliot Wave Breakpoints
| Elliot Wave Breakpoints derived from Fibonacci constants | printed in | tcl wiki format | ||||
|---|---|---|---|---|---|---|
| quantity | value | comment, if any | ||||
| wave number | Breakpoints from Fibonacci numbers | TCL expression from golden ratio | approximate TCL expression from limited series <3,5,8> | comment, if any | ||
| wave 1 : | 161.8% | new bull (+) or bear (-) market and is usually accompanied by sentiment extremes, possible Fibonacci 161.8% plus | expr { 1/.618 } = 1.61803398874989 | |||
| wave 2 : | 61.8% | possible Fibonacci 61.8% or 78.6% retrenchment | expr { 1/$gr } = 0.6180339887499 | |||
| wave 3 : | 161.8% | possible Fibonacci 161.8% advance | expr { 1/$grc } = 1.61803398874989 | |||
| wave 4: | 38.2% | possible Fibonacci 38.2% retrenchment, sideways market | expr { $grc**2} =0.3819660112501052 | expr {5./13}= 0.38461538461539 | ||
| wave 5: | 23.6% | possible Fibonacci final leg in the direction of the dominant trend | expr { $grc**3} = 0.23606797749978975 | expr {5./21.}=0.23809523809523808 | ||
| wave x: | 14.6% | possible Fibonacci dip in the direction of the dominant trend | expr { $grc**4}= 0.14589803375031551 | expr {5./34. }=0.14705882352941177 | available, but rarely cited by brokers | |
| wave 5 or avg wave: | 50.0% | possible Fibonacci final leg, 50.0% used as analyst midpoint and lost shirts | expr { 5./11}=0.454545454545 ( ~ .5) | cited as avg wave by brokers, uncertain derivation from $gr | ||
| Note 1: | notes on Elliott Wave Principle, possible peak curve rises and falls from Fibonacci numbers | |||||
| Note 2: | Elliot wave analyst Fibonacci constants : | 161.8%.,61.8%, 38.2%, 23.6%, and 50.0 % | ||||
| Note : | apparently from OEIS A000045 Fibonacci series,limited set <3,5,8> | |||||
| Note 3: | TCL expressions should be pastable into console window |
From 24 October 1929 to 29 October 1929, the American stock market lost 23 per cent of value. Possibly the Elliot wave analyst Fibonacci constant of 0.236029032 or 23.6% may apply.
Revolution Periods and Distance of Planets from the Sun
This is not an intended use of calculator, but the calculator can work with other consistent units like days, months and distances, simply treating the Golden Ratio constants and Fibonacci sequence numbers as reals. This paragraph largely follows the book “Harmonic Trading” by Scott M. Carney. The planet Venus has a revolution period of 225 Earth days. Enter 225 Earth days in the TCL calculator and receive 364 Earth days, the revolution period of Planet Earth. Alternate hand calculations were expr { 225. * 1./ 0.618 }, 364.0 days. Alternate calculation using the later Fibonnaci sequence numbers as reals was expr { 225. * 1346269. / 832040. }, 364.0 days.
The Titius–Bode law estimated rough distances in Astronomical Units (AU) of Planets from the Sun by scaling powers of 2, Johann Elert Bode, pub 1772. Although much more known in modern times, an examination of the original Titius–Bode results in AU gives some fodder for the theory of the TCL calculator. For example, Titius–Bode law rated Earth as 1 AU from the Sun and predicted Mars as 1.6 AU. The Bode estimate for Mars was short of the true value 1.676 AU by 4.77 percent error. Using hand calculations, a similar value can be ginned up from the golden ratio, expr { $golden_ratio_constant / 1. } returns 1.618 AU rounded. The golden ratio method is still short of the Mars true distance by 3.6 percent error. Numerous excellent papers have used both the Fibonacci and the golden ratio constants methods to estimate planetary distances from the Sun. The Lombardi paper found the best fit to the Fibonacci constants used the scaling constant < K1 = 55.88 > to get E6 km prediction. Both the Fibonacci and Bode sequences have unassigned slots or skips, due to the Asteriod belt(s) and possible undiscovered bodies. The Asteroid Ceres is representative of Asteroid belt here, but was not known to Bode. Also, both Neptune and Pluto not known to Bode in 1772.
Here is an example of how the Fibonacci method might be used with < K1 = 55.88 > . Astronomer Mary Blagg in 1913 conjectured that if the transplutonian Planet X existed, it might be at ~68 AU from the Sun. The nearest Fibonacci constants are 233 and 377, and unassigned at that. Perhaps, expr { 0.349 * 233. } ;# 81.317 AU for Planet X?Th e interest in Planet X and the region of 80 AU is not original or new by any means. Schuette suggested a family of comets in the region of 80 AU aphelia, circa 1949. The perihelion of the object Sedna is around 76 AU, reported in 2004. The perihelion of the object 2012 VP is around 80 AU, reported in 2012.
With additional scale factors loaded in the deck, the TCL calculator could use the Fibonacci sequence to output the planetary distances in kilometers and AU. The scale factor for kilometers is 55.88 (*E6). Sample calculation for Planet X was expr { 233. * 55.88 } ;# returns rounded 13000 X 1E6 km. The scale factor for AU is expr { 19.2 / 55. } ;# ratio of Uranus returns 0.349 AU/Fi
What would be the range window(s) for the hypothetical transplutonian planet X ?
proportions 55 / 19.22 AU = X /68 au
X * 19.2 = 55* 68
x = 55.* 68./19.2
expr { 55.* 68./19.2} ;# returns 194.7 as F estimate
nearest Fibonacci constants are 233 and 377,
and unassigned at that.
expr { 233. * 55.88 } ;# returns rounded 13000 X 1E6 km
expr { 377. * 55.88 } ;# returns rounded 21000 X 1E6 km
expr { 19.2 / 55. } ;# ratio of Uranus returns 0.349 AU/Fi
expr { 0.349 * 233. } ;# 81.317 AU for planet X?
Here is an example of how the Fibonacci method might be used with < K1 = 55.88 > . Astronomer Mary Blagg in 1913 conjectured that if transplutonian planet existed, it might be at ~68 AU from the Sun. The perihelion of Sedna is around 76 AU. The perihelion of 2012 VP is around 80 AU.
;# Pseudocode & Equations
What would be the range window(s) for the hypothetical transplutonian planet X ?
proportions 55 / 19.22 AU = X /68 au
X * 19.2 = 55* 68
X = 55.* 68./19.2
expr { 55.* 68./19.2} ;# returns 194.7 as F estimate
nearest Fibonacci constants are 233 and 377,
and unassigned at that.
expr { 233. * 55.88 } ;# returns rounded 13000 X 1E6 km
expr { 377. * 55.88 } ;# returns rounded 21000 X 1E6 km
;# scale Fibonacci to AU in outer reaches of solar system
expr { 19.2 / 55. } ;# ratio of Uranus returns 0.349 AU/Fi
expr { 0.349 * 233. } ;# 81.317 AU for Planet X? | Table : Est. Distance of Planets from Fibonacci and Bode Rules | printed in tcl wiki format | |||||||
|---|---|---|---|---|---|---|---|---|
| sources >> | JPL | JPL | Fibonacci constants | Lombardi Paper | Lombardi Paper | Wikipedia | Wikipedia | comments |
| quantity | real measured AU, semi_major axis | real measured 10E6 km, semi_major axis | Fibonacci constants | Fibonacci * 55.88, 10E6 km Prediction | Titius-Bode number | Titius-Bode AU Prediction | Real Measured AU , semi_major axis | comments, if any |
| Sun | 0 | 0 | Sun not assigned value in Fibonacci and Bode Rules | |||||
| Mercury | 0.39 | 57.9 | 1 | 55.8 | 4 | 0.4 | 0.39 | |
| Venus | 0.723 | 108.2 | 2 | 111.6 | 7 | 0.7 | 0.72 | |
| Earth | 1 | 149.6 | 3 | 167.4 | 10 | 1 | 1 | Earth assigned unit 1 AU in Bode Rules |
| Mars | 1.524 | 227.9 | 5 | 279 | 16 | 1.6 | 1.52 | |
| Ceres | 8 | 446.4 | 28 | 2.8 | 2.77 | Asteroid belt | ||
| Jupiter | 5.203 | 778.3 | 13 | 725.4 | 52 | 5.2 | 5.2 | |
| Jupiter clearance belt | 21 | 1171.8 | Jupiter clearance belt | |||||
| Saturn | 9.539 | 1427 | 34 | 1897.2 | 100 | 10 | 9.55 | |
| Uranus | 19.18 | 2871 | 55 | 3069 | 196 | 19.6 | 19.22 | |
| Neptune | 30.07 | 4497.1 | 89? | 4966.2 | 388? | 38.8? | 30.11 | Bodes Law breaks down for Neptune and Pluto. Confusing references. |
| Pluto (avg) | 39.482 | 5906.38 | 144? | 8035.2? | 772? | 77.20? | 39.54 | Pluto is not considered a planet, currently. Bodes Law breaks down for Neptune and Pluto. Confusing references. |
| Note | several sources | Wikipedia | Jpl | Lombardi Paper | ||||
| Note | Neptune, Pluto, & Ceres were not known to Bode | |||||||
| Note | Ceres representative of Asteroid belt here | |||||||
| Note | Bodes Law breaks down for Neptune and Pluto, confusing references | Opinion: Bode Number assignment for N&P uncertain here. |
Experimental exchange of affinity pairs in lines 3 and 4 to modify Hexagram with time shift
Refers to the Hexagram time line shift in Yin-Yang cycle of growth from I Ching Oracle Book, increase, and decrease.
gold 1/12/2024
Background. The four affinities are Full Yang Summer, Growing Yin Autumn, Full Yin Winter, Growing Yang Spring. Lines 3 & 4 of the Hexagram pertain to the human endeavors. A possible exchange in Hexagram would substitute either the next affinity pair or the previous affinity pair in the affinity cycle. The four affinity pairs are usually displayed in a circle of four affinities. Each current affinity pair has an affinity pair before and after the current affinity pair in the cycle of growing things, increase in right hand direction, decrease in left hand direction.
Background : The system of affinity pairs relative to the 4 temperate seasons is further divided into "greater yang" (太陽; sun; summer),, "lesser yang" (少陽) Autumn, "greater yin" (太陰; moon; winter), and "lesser yin" (少陰) Spring. A simple and alternate text for the 4 temperate seasons as follows. Sequence of 4 seasons is Full Yang Summer > Growing Yin Autumn > Full Yin Winter > Growing Yang Spring. Note. Some USA website definitions list these affinity pairs in correct order of the four seasons in temperate zone, but caution, not all.
Continuing Thread on Hexagram #21
Example on Hexagram #21. Bottom is Trigram as Earth. Top is Trigram as Sky. The two lines 3 & 4 form the affinity pair, growing Yin. The next and future affinity pair in the Yin-Yang growth cycle to right hand is Full Yin. The previous and past affinity pair in the Yin-Yang growth cycle to right hand is Full Yang. We substitute the next and future affinity pair Full Yin in lines 3 & 4 Hexagram #21 to transform to Hexagram #20.
We substitute the previous and past affinity pair Full Yang into lines 3 & 4 Hexagram #21 to transform to Hexagram #33. Now in interpretation for Hexagram #21, we obtain a past station as Hexagram #33. Previously, We obtained a future station as Hexagram #20.
We have generated a sequence of Hexagrams along the time cycle of Yin-Yang growth cycle. The past H. #33 as Safe in seclusion, the current H. #21 as Effort, and the future H. 20 as Contemplation.
Worked on item last night with my computer program(s). Let me suggest a few additional computer "bits" .... ..... Many Hands and many extra people make light work in China, some say. I am not trained in the specific divination method of "Yada Yada" cited in the post. I do not have all the answers.
Speculations on Time Waves
The original simplified calculations for personal time waves used a set of time waves of constant duration. However, the other textbook calculations for long term historical events used time waves of non constant duration with foreshortening factors over successive time waves. Previous authors do not use the same terms over the foreshortening factors, some report the acceleration of historical events or the quickening. Using a factor of e**(-C1*time) would shorten the successive time waves after the first calculated time cycle (2) or a selected later cycle (3, 4, 5 ...) . To an observer on the original timeline of constant golden cycles, the events might appear to accelerate during his personal timeline. There were some case histories and world events that did not quite match constant waves. But possibly a foreshortening factor or exponential decay in the time waves calculation might be a solution. Another possibility is that the foreshortening factors in the time waves have counterparts in the Elliot wave analyst Fibonacci constants : 161.8%.,61.8%, 38.2%, 23.6%, and 50.0%. One might apply a list of Elliot wave breakpoints on foreshorted waves either as sequence < list 61.8% 38.2% 23.6% 14.6% ...> or sequence f(n) as < list .618**1 .618**2 .618**3 .618**4 .618**5 ...>. Maybe numerical coincidence, but the most convincing example in the textbook of variable time cycles had successive cycle length ratios of < 38.98 39.130 > . These variable length ratios are about 2 percent difference from the Elliot wave 38.2% breakpoint. Given the typical 5% line of significance, estimating cycle wave lengths using the Elliot wave breakpoints may be a feasible study. A constant k1 in exponential decay or exponential rise for the time waves was considered in the early TCL calculator versions, but the personal events over a lifetime seem to be adequate or matched well enough to a set of time waves of constant duration.
Bifurcation is a fork of paths in the timelines. From the standpoint of the observer on the main timeline, a bifurcation or fork may appear as a delay in time, change in time velocity or time acceleration. Based on video work of Gregg Braden.
The switch mode is 1 for normal time waves of constant length. The experimental switch mode is 2.3.4 etc for experimental decay of time waves. The experimental constant_k1 reduces later successive time waves after the occurrence of the first time wave. The decay factor or foreshortening factor may be set on the successive time waves, called the quickening in some quarters. But acceleration of events appears to personal history as observer on timeline. The experimental switch mode is -1, -2, -3,-4 etc for experimental rise and increasing length of successive time waves. The rise factor and extra length may be set on time waves, but deceleration of events appears to personal history as observer on timeline. The original calculator was working pretty well, so the code for initial conditions reports and experimental foreshortening of time waves were put in separate procs and hidden conditional boxes.
The variable_cycle proc is seven textbook stages of arithmetic boiled down into a one line TCL proc. The variable_cycle proc was written for world events and is referenced to calendar years CE. The variable_cycle proc or the "varry" command was nested several times to generate successive waves from a seed_date in calendar years. The TCL calculator may have to >> exit << to clear registers on variable cycle test. In the plotted example below, the same seed date was used here, but 2 entirely different sets of results were generated. The nearest analogy is the marble rolling down the side of a bowl from Galileo Galilei, circa 1564 -1642. The marble is accelerated as dropped down the side of the bowl. when the marble rolls on the flattish bottom of bowl, it will continue at a constant speed like on a level plain. But when the marble arrives at the other side of the bowl, the marble begins to climb and decelerate. As the marble continues to climb, it loses speed and constant time segments along the X axis "timeline" would appear to shorten in length.
Gist. The constant time wave calculations were referenced to a individual lifetime. But the variable time waves in years CE were referenced to the Mayan calendar time cycle of 5125.0 years and the Earth procession cycle of 25625.0 years. There are 5 Mayan time cycles over a procession period. The TCL expression is expr < 25625.0 / 5. > returns 5. time cycles. The year Zero is for Mayan date 0.0.0.0.0, which translates to August 11, 3114 BCE. So then, the start date of the Mayan calendar system for our calculations was 3113. years BCE. Effectively, each variable time wave is rescaled by the fraction <.618*(($seed_date + 3113.)/5125.))>. The variable time wave length approaches the asymptotic near the end of the current Mayan time cycle, 5125. years. The end of the current Mayan time cycle is converted to 2012 CE'''.
As an aside, the Mayan Astronomers used the Zero about 1200 years before common use in Europe. The Mayans used the Zero in their Mayan calendar calculations and did not have the European confusion of the original Julian calendar in lacking the year Zero.
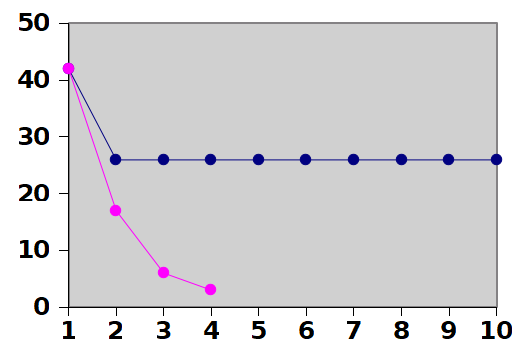
Figure . Contrast between Results on constant length and variable_length_waves
Here the same seed date was used, but > 2 < entirely different sets of results were generated.
| table of USA enters WWII | printed in TCL format | |
|---|---|---|
| seed_date | year cycle | comment, if any |
| seed_date 1941.12 | ||
| seed_date 1941.12 | varry 1984.3 | |
| seed_date 1941.12 | varry 2001.3 | |
| seed_date 1941.12 | varry 2007.9 | |
| seed_date 1941.12 | varry 2010.4 |
;# variable_cycle proc is referenced to calendar years CE
set seed_date 1941.12
set yearx [ expr { ($seed_date + 3113.) + ((5125.-($seed_date + 3113.))*.618*(($seed_date + 3113.)/5125.))-3113. } ]
set precessional_cycle 25625.
;# expr { 25625./5125 } ;# returns 5.0
set mayan_cycle 5125.
;# if seed_date approaches 2012 or end of current mayan_cycle 5125,
;# one might increase mayan_cycle to avoid asymptotic.
;# if { $seed_date > 1992.} { set mayan_cycle 5175.}
proc variable_cycle { mayan_cycle seed_date } {expr { ($seed_date + 3113.) + (($mayan_cycle-($seed_date + 3113.))*.618*(($seed_date + 3113.)/$mayan_cycle))-3113. } }
proc variable_function { seed_date cycles_needed } {... }
Robert G. Sacco described some novel features of Fibonacci waves in modeling celestial mechanics. As the Fibonacci sequence progresses, the ratio values of successive Fibonacci terms oscillate or have a sine motion in reference to the asymptote value of the Golden Ratio constant. If one adds a plus or minus to the calculated ratio relative to the Golden Ratio constant, the set of Fibonacci ratios has a sine or on-off component. The set of Fibonacci ratios would look like < 1/1(-) 2/1(+) 3/2(-) 5/3(+) 8/5(-) 13/8(+) 21/13(-) 34/21(+) 55/34(-) 89/55(+) ... 1.618 = Golden Ratio constant > for increasing planetary distances in celestial mechanics. As might be expected, the sequence for the Golden Mean Conjugate is the opposite phase of the golden Mean. Returning to the TCL calculator, it should be possible to model the time waves in the TCL calculator with these oscillating Fibonacci ratios. But may have to use the complementary sequence for the Golden Ratio conjugate (0.618) as < 1/1(+) 1/2(-) 2/3(+) 3/5(-) 5/8(+) 8/13(-) 13/21(+) 21/34(-) 34/55(+) 55/89(-) ... 0.618 = Golden Ratio conjugate >. Normalized, the tentative reduction factors would be < list 1. 0.5 0.333 0.6 0.625 0.619 0.61818 0.6179 ... Golden Ratio conjugate >
Fractal Limits of the simulated reality from Koch snowflake
Fractal Code of the simulated reality is similar to repetitive patters in our lives, per lecture of Gregg Braden. Repetitive patters in our lives hows fractal growth is limited. Koch snowflake. Area or growing curve of Koch snowflake has 1.6X limit. Koch snowflake has 1.6X limit to area growth of fractal pattern. First area increase of Koch snowflake is 1/3, 2nd iteration is 4/27, 3ird iteration is 16/243, 4th iteration is 64/2187. The area limit is 1.6X. Perimeter or edge of fractal simulation can change to infinite complexity. How long fractal pattern or simulation lasts? How complex edge or perimeter can become? The limiting scale of universe may called the planck length, which means there may be a limit to how large the universe may become, quoting Steven Hawking.
Test Suite on Time Fractals in Golden Ratio Proportions
The calculations of time fractals in golden ratio proportions have problems with initial conditions and observer reference issues. There are two possible methods of time fractal calculations, either the seed year as personal age or the seed year as a Gregorian calendar year. The seed age event and birthdays are different for most people in the personal age method. The optional test suite has added the calculations for a golden date from a Gregorian calendar year.
Pushbutton Operation
For the push buttons on the TCL calculator, the recommended procedure is push testcase and fill frame, change first three entries etc, push solve, and then push report. Report allows copy and paste from console. For testcases in a computer session, the TCL calculator increments a new testcase number internally, eg. TC(1), TC(2) , TC(3) , TC(N). The testcase number is internal to the calculator and will not be printed until the report button is pushed for the current result numbers. The current result numbers will be cleared either on the next clear button or on the next solve button.
Conclusions
The TCL calculator seems to be working as it stands and matches the scanty textbook examples. Additional significant figures are used to check the TCL program, not to infer the accuracy of inputs and product reports. The brokers rarely use more than 3 significant figures. This is the only internet article that carries the Elliot wave constants to 17 places, but that might be a service to a student. The calculator carries the numbers out to the TCL 8.6 maximum (17 places), but suggest there is about a 5 per cent accuracy inherent in most inputs and the probable event outputs. One relative error calculation in TCL notation was vis expr {(1 -(28.797 / 27.506))* 100. } >> 4.69 percent accuracy.
Pseudocode, Equations, and Wiki Page Checklist
#pseudocode can be developed from rules of thumb.
#pseudocode: some problems can be solved by proportions (rule of three), to some order of magnitude
#pseudocode: enter quantity1, quantity2, quantity3 and expected output (quantity4) for testcases.
#pseudocode: enter time in years, number of remaining items
#pseudocode: output fraction of (remaining items) over (items at time zero)
#pseudocode: ouput remaining items as fraction or percent
#pseudocode: output fraction of (quantity4 ) over ( quantity1 at time zero)
#pseudocode: output fraction of (quantity2) * (quantity3 ) over (quantity1 at time zero)
#pseudocode: outputs should be in compatible units.
#pseudocode: rules of thumb can be 3 to 15 percent off, partly since g..in g..out.
#pseudocode: need test cases > small,medium, giant
#pseudocode: need testcases within range of expected operation.
#pseudocode: are there any cases too small or large to be solved?
#
# F(N+1) == F(N) + F(N-1)
# F(1) == 1
# F(2) == 1
set Grade_School 6
set Middle_School 2
set High_School 4
set College 4
set Graduate_School 2
set values [list 6 8 12 16 18]
set fractals [list 9.7 12.94 19.4 25.888 29.14]
partials, f(1)= .5
f(2) = (1/4) * .5
f(3) = (1/6) * .5
Testcases Section
In planning any software, it is advisable to gather a number of testcases to check the results of the program.
Testcase 1, Test on Human Life Cycles
| table 1 | printed in | tcl wiki format |
|---|---|---|
| quantity | value | comment, if any |
| 1: | testcase_number | |
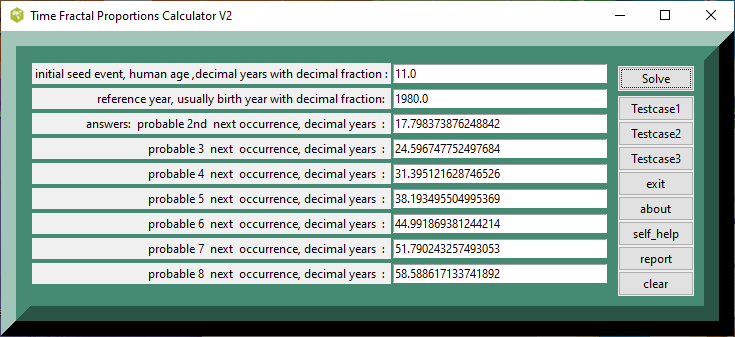
| 11.0 : | initial age decimal years | |
| 17.798373876248842 : | answers: probable 2nd next occurrence, decimal years : | |
| 24.596747752497684 : | probable 3 next occurrence, decimal years : | |
| 31.395121628746526 : | probable 4 next occurrence, decimal years : | |
| 38.193495504995369 : | probable 5 next occurrence, decimal years : | |
| 44.991869381244214 : | probable 6 next occurrence, decimal years : | |
| 51.790243257493053 : | probable 7 next occurrence, decimal years : | |
| 58.588617133741892 : | probable 8 next occurrence, decimal years : |
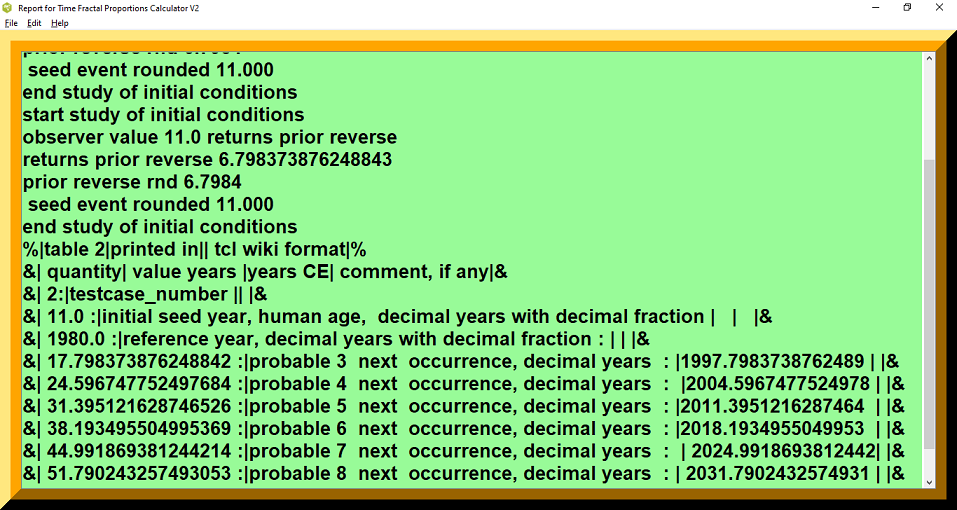
;# printout start study of initial conditions observer value 17.792999999999999 returns prior reverse returns prior reverse 10.996678761826878 prior reverse rnd 10.997 seed event rounded 17.793 end study of initial conditions %|table 1|printed in| tcl wiki format|%
Testcase 2, Human Life Cycles
| table 2 | printed in | tcl wiki format |
|---|---|---|
| quantity | value | comment, if any |
| 2: | testcase_number | |
| 16.0 : | initial age decimal years | |
| 25.888543819998318 : | answers: probable 2nd next occurrence, decimal years : | |
| 35.777087639996637 : | probable 3 next occurrence, decimal years : | |
| 45.665631459994955 : | probable 4 next occurrence, decimal years : | |
| 55.554175279993274 : | probable 5 next occurrence, decimal years : | |
| 65.442719099991592 : | probable 6 next occurrence, decimal years : | |
| 75.331262919989911 : | probable 7 next occurrence, decimal years : | |
| 85.219806739988229 : | probable 8 next occurrence, decimal years : |
;# printout start study of initial conditions observer value 16.0 returns prior reverse returns prior reverse 9.8885438199983167 prior reverse rnd 9.8885 seed event rounded 16.000 end study of initial conditions ##### start study of initial conditions observer value 25.888000000000002 returns prior reverse returns prior reverse 15.999663900757277 prior reverse rnd 16.000 seed event rounded 25.888 end study of initial conditions
Testcase 3, Human Teenager Trial
| table 3 | printed in | tcl wiki format |
|---|---|---|
| quantity | value | comment, if any |
| 3: | testcase_number | |
| 10.0 : | initial age decimal years | |
| 16.180339887498949 : | answers: probable 2nd next occurrence, decimal years : | |
| 22.360679774997898 : | probable 3 next occurrence, decimal years : | |
| 28.541019662496847 : | probable 4 next occurrence, decimal years : | |
| 34.721359549995796 : | probable 5 next occurrence, decimal years : | |
| 40.901699437494742 : | probable 6 next occurrence, decimal years : | |
| 47.082039324993694 : | probable 7 next occurrence, decimal years : | |
| 53.262379212492647 : | probable 8 next occurrence, decimal years : |
;# printout start study of initial conditions observer value 10.0 returns prior reverse returns prior reverse 6.1803398874989481 prior reverse rnd 6.1803 seed event rounded 10.000 end study of initial conditions start study of initial conditions observer value 16.18 returns prior reverse returns prior reverse 9.9997899379732971 prior reverse rnd 9.9998 seed event rounded 16.180 end study of initial conditions
Testcase 4, Predicted Human Teenager
| table 8 | printed in | tcl wiki format |
|---|---|---|
| quantity | value | comment, if any |
| 8: | testcase_number | |
| 15.0 : | initial age decimal years | |
| 24.270509831248422 : | answers: probable 2nd next occurrence, decimal years : | |
| 33.541019662496844 : | probable 3 next occurrence, decimal years : | |
| 42.811529493745269 : | probable 4 next occurrence, decimal years : | |
| 52.082039324993687 : | probable 5 next occurrence, decimal years : | |
| 61.352549156242105 : | probable 6 next occurrence, decimal years : | |
| 70.623058987490538 : | probable 7 next occurrence, decimal years : | |
| 79.893568818738956 : | probable 8 next occurrence, decimal years : |
;# printout start study of initial conditions observer value 15.0 returns prior reverse returns prior reverse 9.2705098312484218 prior reverse rnd 9.2705 seed event rounded 15.000 end study of initial conditions start study of initial conditions observer value 24.27 returns prior reverse returns prior reverse 14.999684906959946 prior reverse rnd 15.000 seed event rounded 24.270 end study of initial conditions
Testcase 5a, Successive Fibonacci constants
This is not intended use of calculator, but the calculator can generate Successive Fibonacci sequence numbers as reals. If the entry is a Fibonacci number greater than zero, the TCL calculator should approximate the next successive Fibonacci numbers as reals, but need to round to nearest integer. The On-Line Encyclopedia of Integer Sequences A000045 gives the Fibonacci numbers as follows 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, 28657, 46368, 75025, 121393, 196418, 317811, 514229, 832040, 1346269.
| table 5a,Successive Fibonacci constants | n | printed in tcl wiki format |
|---|---|---|
| quantity | value | comment, if any |
| 10: | testcase_number | |
| 144.0 : | initial age decimal years | |
| 232.99689437998484 : | answers: probable 2nd next occurrence, decimal years : | |
| 321.99378875996968 : | probable 3 next occurrence, decimal years : | |
| 410.99068313995451 : | probable 4 next occurrence, decimal years : | |
| 499.98757751993935 : | probable 5 next occurrence, decimal years : | |
| 588.98447189992419 : | probable 6 next occurrence, decimal years : | |
| 677.98136627990903 : | probable 7 next occurrence, decimal years : | |
| 766.97826065989386 : | probable 8 next occurrence, decimal years : |
;# printout start study of initial conditions observer value 144.0 returns prior reverse returns prior reverse 88.996894379984852 prior reverse rnd 88.997 seed event rounded 144.00 end study of initial conditions start study of initial conditions observer value 232.99600000000001 returns prior reverse returns prior reverse 143.99944724277049 prior reverse rnd 144.00 seed event rounded 233.00 end study of initial conditions
Testcase 5b, Stock Markets, Fibonacci constants
| table 5b | printed in | tcl wiki format |
|---|---|---|
| quantity | value | comment, if any |
| 5b: | notes on Elliott Wave Principle, possible peak curve rises and falls from Fibonacci numbers | |
| wave number | entry (144) is Fibonacci number | |
| wave 1 : | 161.8% | new bull (+) or bear (-) market and is usually accompanied by sentiment extremes, possible Fibonacci 161.8% plus |
| wave 2 : | 61.8% | possible Fibonacci 61.8% or 78.6% retrenchment |
| wave 3 : | 161.8% | possible Fibonacci 161.8% advance |
| wave 4: | 38.2% | possible Fibonacci 38.2% retrenchment, sideways market |
| wave 5: | 32.6% | possible Fibonacci final leg in the direction of the dominant trend |
| wave 5: | 50.0% | possible Fibonacci final leg, 50.0% used as analyst midpoint and lost shirts |
| Elliot wave analyst Fibonacci constants : | 161.8%.,61.8%, 38.2%, 23.6%, and 50.0 % | apparently from OEIS A000045 Fibonacci series, <3,5,8> |
Testcase 6a, life cycle of cicada insect and a separate cicada species
,# printout start study of initial conditions observer value 13.0 returns prior reverse returns prior reverse 8.034441853748632 prior reverse rnd 8.0344 seed event rounded 13.000
| table 6a | printed in | tcl wiki format |
|---|---|---|
| quantity | value | comment, if any |
| 6a : | testcase_number | |
| 11.0 : | initial age decimal years | solar cycle of eleven years |
| 17.798373876248842 : | answers: probable 2nd next occurrence, decimal years. life cycle of cicada insect : | |
| 24.596747752497684 : | probable 3 next occurrence, decimal years : | |
| 31.395121628746526 : | probable 4 next occurrence, decimal years : | |
| 38.193495504995369 : | probable 5 next occurrence, decimal years : | |
| 44.991869381244214 : | probable 6 next occurrence, decimal years : | |
| 51.790243257493053 : | probable 7 next occurrence, decimal years : | |
| 58.588617133741892 : | probable 8 next occurrence, decimal years : |
;# printout start study of initial conditions observer value 11.0 returns prior reverse returns prior reverse 6.798373876248843 prior reverse rnd 6.7984 seed event rounded 11.000 end study of initial conditions start study of initial conditions observer value 17.0 returns prior reverse returns prior reverse 10.506577808748212 prior reverse rnd 10.507 seed event rounded 17.000 end study of initial conditions %|table 14|printed in| tcl wiki format|%
Note on Hand Calculations for "bug" of 17 years
17.4 years * 0.618 = 10.753 years 17.4 years * 0.382 = 6.647 years Time rise 10.753 years + Time decline 6.647 years = 17.4 total years, Calculations for 17 year life span of Cicada Magicicada ( a species.)
Calculations are carried to 3 decimal places for TCL calculator check, beyond normal significant figures. Probable Accuracy in years was +- 0.5 years. In other words, numbers should be rounded to nearest tenth 0.1 year.
Testcase 6b, Life cycle of a separate cicada species
| table 6b, Life cycle of separate cicada species | printed in | tcl wiki format |
|---|---|---|
| quantity | value | comment, if any |
| 6b: | testcase_number | |
| 8.0 : | initial age decimal years | unknown factor for separate species |
| 12.944271909999159 : | answers: life cycle of cicada insect species, decimal years : | |
| 17.888543819998318 : | probable 3 next occurrence, decimal years : | |
| 22.832815729997478 : | probable 4 next occurrence, decimal years : | |
| 27.777087639996637 : | probable 5 next occurrence, decimal years : | |
| 32.721359549995796 : | probable 6 next occurrence, decimal years : | |
| 37.665631459994955 : | probable 7 next occurrence, decimal years : | |
| 42.609903369994115 : | probable 8 next occurrence, decimal years : | |
| 12.944 : | probable 1st next occurrence, rounded or clipped : | life cycle of cicada insect, separate species |
| Elliot wave analyst Fibonacci constants : | 161.8%.,61.8%, 38.2%, 23.6%, and 50.0 % | apparently from OEIS A000045 Fibonacci series, <3,5,8> |
| breakpoint from alternate Elliot wave theory : | expr { 10. * ( 1. + 100.* 38.2% ) } 13.8 decimal years | Elliot wave theory , not proof of causation. |
;# printout start study of initial conditions observer value 8.0 returns prior reverse returns prior reverse 4.9442719099991583 prior reverse rnd 4.9443 seed event rounded 8.0000 end study of initial conditions start study of initial conditions observer value 13.0 returns prior reverse returns prior reverse 8.034441853748632 prior reverse rnd 8.0344 seed event rounded 13.000 end study of initial conditions %|table 16|printed in| tcl wiki format|%
***
SCRATCH SHEET Note on Hand Calculations. 13 years * 0.618 = 8.034 years 13 years * 0.382 = 4.966 years Time rise 8.034 years + Time decline 4.966 years = 13 total years, 13v year life span of Cicada Magicicada ( a different species.)
Calculations are carried to 3 decimal places for TCL calculator check, beyond normal significant figures. Probable Accuracy in years was +- 0.5 years. In other words, numbers should be rounded to nearest tenth 0.1 year.
;# wave analyst Fibonacci constants
;# using Fibonacci series
expr 5./11 = 0.4545 ( ~ .5)
expr 5./13 = 0.38461538461538464
expr 5./21 = 0.23809523809523808
expr 5./34 = 0.14705882352941177
;# wave analyst Fibonacci constants
;# using golden ratio
expr { 1/.618 } = 1.618
expr { 1/1.618 } = 0.6180469715698392
expr { .618 *.618 } = 0.381924
expr { .618 *.618 *.618 } = 0.236029032
expr { .618 *.618 *.618*.618 } = 0.14586594177599999Testcase 7, Puberty at 13 years old
Most agree that humans start puberty at 13 years old and become mature at 21 years. Enter 13 years for puberty in calculator and receive rounded 21 years for human maturity.
| table 17 | printed in | tcl wiki format |
|---|---|---|
| quantity | value | comment, if any |
| 17: | testcase_number | |
| 13.0 : | initial age decimal years | |
| 21.034441853748632 : | answers: probable 2nd next occurrence, decimal years : | |
| 29.068883707497264 : | probable 3 next occurrence, decimal years : | |
| 37.103325561245896 : | probable 4 next occurrence, decimal years : | |
| 45.137767414994528 : | probable 5 next occurrence, decimal years : | |
| 53.17220926874316 : | probable 6 next occurrence, decimal years : | |
| 61.206651122491792 : | probable 7 next occurrence, decimal years : | |
| 69.241092976240424 : | probable 8 next occurrence, decimal years : |
#; start study of initial conditions observer value 13.0 returns prior reverse returns prior reverse 8.034441853748632 prior reverse rnd 8.0344 seed event rounded 13.000 end study of initial conditions
Testcase 8, Width and Height of DNA Strand
| table 8, Width and Height of DNA Strand | printed in wiki format | |
|---|---|---|
| quantity | value | comment, if any |
| 8: | testcase_number | |
| 21.0 : | angstroms width | |
| 33.978713763747791 : | answers: probable 2nd next occurrence, angstroms : | |
| 46.957427527495582 : | probable 3 next occurrence, decimal years : | |
| 59.936141291243374 : | probable 4 next occurrence, decimal years : | |
| 72.914855054991165 : | probable 5 next occurrence, decimal years : | |
| 85.893568818738956 : | probable 6 next occurrence, decimal years : | |
| 98.872282582486747 : | probable 7 next occurrence, decimal years : | |
| 111.85099634623454 : | probable 8 next occurrence, decimal years : |
start study of initial conditions observer value 21.0 returns prior reverse returns prior reverse 12.978713763747791 prior reverse rnd 12.979 seed event rounded 21.000 end study of initial conditions
proc reverse_time_fractal {age_years} {
set g_constant 1.61803398874989484820
set reverse_time_fractal [ expr { $age_years * (1./$g_constant) } ]
;#return $reverse_fractal
}Testcase 10, Starfish has 5 arms
| table 10, Starfish has 5 arms | printed in | tcl wiki format |
|---|---|---|
| quantity | value | comment, if any |
| 10: | testcase_number | |
| 8.0 : | centimeters between 2 adjacent arms | |
| 12.944271909999159 : | answers: maximum starfish dimensions across 2 opposing arms : | |
| 17.888543819998318 : | probable 3 next occurrence, decimal years : | |
| 22.832815729997478 : | probable 4 next occurrence, decimal years : | |
| 27.777087639996637 : | probable 5 next occurrence, decimal years : | |
| 32.721359549995796 : | probable 6 next occurrence, decimal years : | |
| 37.665631459994955 : | probable 7 next occurrence, decimal years : | |
| 42.609903369994115 : | probable 8 next occurrence, decimal years : |
Testcase 11, Ratio of male bees to female bees in hive
| table 11, Ratio of male bees to female bees in hive | printed in | tcl wiki format |
|---|---|---|
| quantity | value | comment, if any |
| 11: | testcase_number | |
| 10000.0 : | number of male bees | |
| 16180.339887498947 : | answers: number of female bees : | |
| 22360.679774997894 : | probable 3 next occurrence, decimal years : | |
| 28541.019662496841 : | probable 4 next occurrence, decimal years : | |
| 34721.359549995788 : | probable 5 next occurrence, decimal years : | |
| 40901.699437494739 : | probable 6 next occurrence, decimal years : | |
| 47082.039324993682 : | probable 7 next occurrence, decimal years : | |
| 53262.379212492626 : | probable 8 next occurrence, decimal years : |
Testcase 12, Example of Joe Blow in the Mills of Time
| table 12a, Example of Joe Blow in the Mills of Time, set of Golden Time Waves, | printed in tcl wiki format | ||
|---|---|---|---|
| quantity | value years | years CE | comment, if any |
| 1: | testcase_number | ||
| 13.195 : | initial seed year, human age, decimal years with decimal fraction | ||
| 1980.508 : | reference year, birth year, decimal years with decimal fraction : | ||
| 8.1549584815548641 : | estimated golden_time_cycle, decimal years with decimal fraction : | ||
| 8.1550 : | rounded golden_time_cycle, decimal years : | ||
| 13.195 : | initial seed year, first occurrence, decimal years : | 1993.703 | |
| 21.34995 : | probable 3 next occurrence, decimal years : | 2001.85795 | |
| 29.50491 : | probable 4 next occurrence, decimal years : | 2010.0129 | |
| 37.65987 : | probable 5 next occurrence, decimal years : | 2018.16787 | |
| 45.81483 : | probable 6 next occurrence, decimal years : | 2026.32283 | simultaneous event on sets 12a and 12 |
| 53.96979 : | probable 7 next occurrence, decimal years : | 2034.4777 | |
| 62.12475 : | probable 8 next occurrence, decimal years : | 2042.63275 | |
| 70.27970 : | probable 9 next occurrence, decimal years : | 2050.78770 |
<print out report> Console wrapper for solution proc *************************** *************************** start study of initial conditions observer value 13.195 returns prior reverse returns prior reverse 8.1549584815548624 prior reverse rnd 8.1550 seed event rounded 13.195 estimated golden_time_cycle rounded 8.1550 end study of initial conditions output set of results in years 0.000001 13.195 21.349958481554864 29.504916963109729 37.659875444664593 45.814833926219457 53.969792407774321 62.124750889329185 output street_life_male_avg in human age years 0.0000001 13. 18. 21. 24. 29.8 36.5 43.5 55. 60. 65. 73. output rounded set of results in years 0.0000 13.195 21.350 29.505 37.660 45.815 53.970 62.125 output street_life_male_avg in Gregorian years 1980.5 1993.5 1998.5 2001.5 2004.5 2010.3 2017.0 2024.0 2035.5 2040.5 2045.5 2053.5 output rounded set of results in Gregorian years 1980.5 1993.7 2001.9 2010.0 2018.2 2026.3 2034.5 2042.6
| table 12b, Simultaneous set of Golden Time Waves, ref Joe Blow | printed in tcl wiki format | ||
|---|---|---|---|
| quantity | value years | years CE | comment, if any |
| 2: | testcase_number | ||
| 16.0 : | initial seed year, human age, decimal years with decimal fraction | ||
| 1980.0 : | reference year, birth year, decimal years with decimal fraction : | ||
| 9.8885 : | estimated golden_time_cycle, decimal years with decimal fraction : | ||
| 9.8885 : | rounded golden_time_cycle, decimal years : | ||
| 16.0 : | initial seed year, first occurrence, decimal years : | 1996.0 | |
| 25.8885 : | probable 3 next occurrence, decimal years : | 2005.88854 | |
| 35.7770 : | probable 4 next occurrence, decimal years : | 2015.7770 | |
| 45.6656 : | probable 5 next occurrence, decimal years : | 2025.6656 | simultaneous event on sets 12a and 12b |
| 55.5541 : | probable 6 next occurrence, decimal years : | 2035.5541 | |
| 65.4427 : | probable 7 next occurrence, decimal years : | 2045.4427 | |
| 75.3312 : | probable 8 next occurrence, decimal years : | 2055.3312 | |
| 85.2198 : | probable 9 next occurrence, decimal years : | 2065.2198 |
Testcase 13, Examples of Variable Time Waves Referenced to Calendar Years
Credit: Examples from Fractal Time: The Secret of 2012 and a New World Age by Gregg Braden
| table on 1929 stock crash | printed in TCL format | |
|---|---|---|
| seed_date | year cycle | comment, if any |
| seed_date 1929 | seed_date | |
| seed_date 1929 | varry 1979.4 | |
| seed_date 1929 | varry 1999.4 | |
| seed_date 1929 | varry 2007.1 | |
| seed_date 1929 | varry 2010.1 |
| table of USA enters WWII | printed in TCL format | |
|---|---|---|
| seed_date | year cycle | comment, if any |
| seed_date 1941.12 | ||
| seed_date 1941.12 | varry 1984.3 | |
| seed_date 1941.12 | varry 2001.3 | |
| seed_date 1941.12 | varry 2007.9 | |
| seed_date 1941.12 | varry 2010.4 |
| table of first Atomic Bomb in Warfare | printed in TCL format | |
|---|---|---|
| seed_date | year cycle | |
| seed_date 1945 | ||
| seed_date 1945 | varry 1985.8 | |
| seed_date 1945 | varry 2001.9 | |
| seed_date 1945 | varry 2008.1 | |
| seed_date 1945 | varry 2010.5 |
Screenshots Section
figure 1a. Golden_Ratio_screenshot
figure 1b. Time_Fractals_in_Golden_Ratio_report_card
figure 2.time_fractals_equation
figure 3.time_fractal_dummy_curve
figure 4. Time_Fractal_Starfish
figure 5.Golden_Ratio_Proportions
figure 6.Golden_Ratio_definition
figure 7. Golden_Ratio_waves
figure 7b. Proportions Freytag pyramid
figure 7c. Proportions Freytag pyramid 2
photo credit = freytag triangle from chris airiau
figure 7e.Golden_Ratio_waves, simulation in ripple tank
photo credit, ripple tank at falstad.com website.
Golden_Ratio_waves_ripple_tank
figure 8.Golden_Ratio_waves_2, simulation in ripple tank
photo credit, ripple tank at falstad.com website.
figure 9. constant_length_waves from Joe Blow example
figure 10. variable_length_waves from 1941 seed_date example
figure 11. Cicada studying math
photo credit, Sagar Vasnani at Unsplash website.
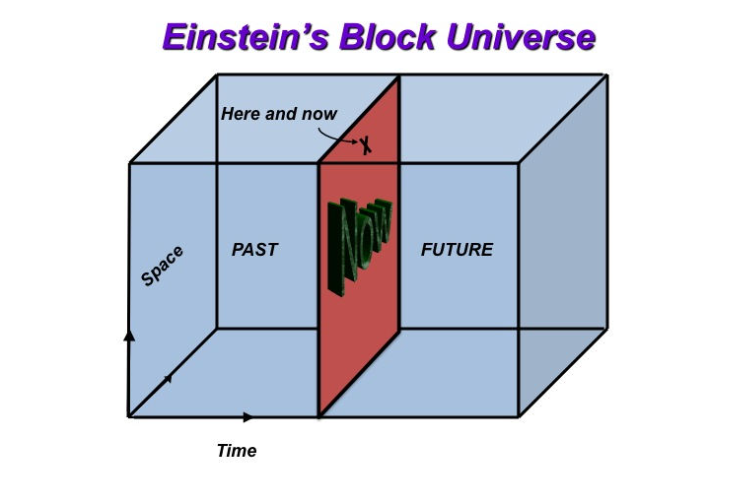
figure 12. Albert Einstein block Universe
Diagram on Conventional Theory of Time , prior to Plank and Quantum Physics circa 1925 . Time is shown treated as 4th dimension in equations.
figure 13. Albert Einstein, John Archibald Wheeler
figure 14. model using poker chips
Stacked poker chips representing Past, Present, and Future are stacked in the Quantum Field. The Here, There, and All Highest on Mountain are stacked with the little "i am" folks and the big " I AM " . Counting down or up in a stack is same as traveling through Wormhole.
figure 15. Wormhole
The info content as blurred spheres in pix is both " here " and " there " in the Quantum Field, traveling through the worm hole. I like my stacked poker chips better. The straight path is same as conventional Newtonian travel in the the Einstein 4D model.
figure 16. Multiple Universes
Bubbles effect in exploding Multiverse, parallel worlds, parallel universes, mirros of current time status. You are in good health in one of these mirrors.
References:
- Wikipedia search engine < time >
- Wikipedia search engine < golden ratio proportions >
- Wikipedia search engine < Fibonacci >
- Google search engine < fractal time calculator Braden Greg >
- Book >> Fractal Time: The Secret of 2012 and a New World Age
- Paperback – Illustrated, February 1, 2010
- book(s) by Braden Gregg
- www.greggbraden.com/fractal time calculator
- Website articles by Tony Spilotro
- Bitcoin Mathematics: Why 21 Million BTC May Have Been Chosen
- Extreme interest in trading Bitcoin cryptocurrency golden ratio tops
- Fibonacci Day: How To Use Math To Trade Bitcoin And Altcoins
- Web article Mathematical Mystery: Why Did The Bitcoin Rally Stop At The Golden Ratio?
- Crypto Calculated: How Ancient Math Predicts Bitcoin’s Next Top At $270K
- Fibonacci Day: How To Use Math To Trade Bitcoin And Altcoins
- by Tony Spilotro
- Understanding Bitcoin’s Market Cycles: 3 Simple indicators for future tops and bottoms
- Collected Works of R. N. Elliot
- The Wave Principle. Nature's Law: The Secret of the Universe. R. N. Elliot
- Series of Articles Published in 1939 by Ralph Nelson Elliott.
- Elliott Wave Principle by A.J. Frost and Robert Prechter
- Elliott Wave Principle: Key To Market Behavior
- Elliott, Ralph Nelson, Frost, Alfred John, Prechter, Robert Rougelot
- R.N. Elliott's Masterworks: The Definitive Collection
- 318 Pages · 1994 English
- by R. N. Elliott & Robert R. Prechter & Jr.
- Fractal Time. coded in python , sourceforge.net_projects_fractaltimecalc
- Golden Ratios in Energy Radiation and Vibrations
- May 23, 2012 by Gary Meisner 1.6180339887498948420
- Terence McKenna. 1998, TimeWave Zero Software
- Essay: Timewave Zero .Pdf by Terence McKenna
- contributions on Time Code Software by Peter Meyer.
- Peter J. Meyer , Peter Johann Gustav Meyer, born 1946
- Mathematics of Timewave Zero by Peter Meyer.
- appeared in the Invisible Landscape, 2nd edition, HarperCollins, 1993
- www.science20.com/hammock_physicist/fibonacci_butterflies
- by Johannes Koelman, August 6th 2009
- en.wikipedia.org/wiki/Anosov_diffeomorphism, Dmitri Victorovich Anosov
- Fractal universe and the speed of light: Revision of the universal constants
- Antonio Alfonso-Faus
- Weinberg, S. (1972) Gravitation and Cosmology. Wiley,
- Timewave Synthesizer at SourceForge
- waveform synthesizer based upon Timewave Zero theory by Terence McKenna
- David Wallace on The Arrow of Time
- Time Arrow, Many worlds interpretation, buzzwords, wow
- time processes forward and backward?
- REWIND (tape, not time!) => Fortran command, remember.
- podcast/2021/08/02/158-david-wallace-on-the-arrow-of-time
- Planck length, en.wikipedia.org/wiki/Stephen_Hawking
- High School geometry class to the rescue.
- On Constructing the Universe From Scratch
- JANUARY 8, 2016, Bruce Camber
- bblu.org/2016/01/08/number
- A mathematical analysis of the Koch curve and quadratic Koch curve, pdf
References: Elliott Wave Theory, Stock Markets
- Scott M. Carney. Harmonic Trading, FT Press, 2010
- Elliott Wave Principle by A.J. Frost and Robert Prechter
- Elliott Wave Principle: Key To Market Behavior
- Elliott, Ralph Nelson, Frost, Alfred John, Prechter, Robert Rougelot
- R.N. Elliott's Masterworks: The Definitive Collection
- 318 Pages · 1994 English
- by R. N. Elliott & Robert R. Prechter & Jr.
References: Fractal Waves and Fractal Limits
- Koch Snowflake Modeling Growth and TCL demo example calculator, numerical analysis
- Wikipedia search engine < Koch Snowflake >
- Video :Gregg Braden - Fractal Code of the Simulated Reality
- = Repetitive Patters in Our Lives
- shows fractal limit, growing curve of growing snowflake, 1.6X limit
- Planck length, en.wikipedia.org/wiki/Stephen_Hawking
- Planck time granularity, en.wikipedia.org/wiki/Stephen_Hawking
- A mathematical analysis of the Koch curve and quadratic Koch curve, pdf
References: Planets, Titius–Bode law
- wikipedia.org/wiki/Titius Bode law
- Article: All Solar system periods fit
- the Fibonacci series and the Golden Ratio.
- Posted: February 20, 2013 by tallbloke
- The Golden Mean In The Solar System,
- Oreste W. Lombard I And Margaret A. Lombardi
- On a Suggested Substitute for Bode’s Law. By M. A. Blagg.
- Communicated by Professor H. B. Turner.
- Planetary distances: a new simplified model
- Sven-Ingmar Ragnarsson, 1994
- Fibonacci Series In The Solar System
- Captain B. A. Read, Canada
- A postulate leading to the Titius-Bode law
- R. Louise
- www.jpl.nasa.gov/edu/pdfs/scaless_reference.pdf
- Schuette, C. H., "Two new families of comets", Pop. Astron. 57, 176-82
- (1949); "Drei weitere Mitglieder der Transplutokometenfamilie", Acta
- Astronomica 15, 11-13 (1965).
- Bode’s Law And Spiral Structure In Nebulae
- By William Sutherland
- A Sedna-like body with a perihelion of 80
- astronomical units
- Chadwick A. Trujillo, Scott S. Sheppard
- Searching For Sedna’s Sisters: Exploring The Inner Oort Cloud
- Megan Schwamb with Advisor: Mike Brown
- A new object at the edge of our Solar System discovered
- by Carnegie Institution for Science
- Modeling Celestial Mechanics Using the Fibonacci Number,
- Robert G. Sacco, 2019
References: cicada insects
- Stephen Gould, essay “Of Bamboo, Cicadas, and the Economy of Adam Smith,” paleontologist
- Stephen Gould, book >> Ever Since Darwin
- Peter Gwin, Overhead National Geographic Podcast
- Podcast. How come Cicadas are so good at math?
- Hosted by Peter Gwin and Amy Briggs.
- Chris Simon, cicada expert, University of Connecticut
- www.cicadamania.com/cicadas/, delightful website
- Cicadas showing up after a prime number of years
- Author(s): Mario Markus;
Appendix Code
appendix TCL programs and scripts
# pretty print from autoindent and ased editor occurrence
# Time Fractal Proportions calculator
# written on Windows 10
# working under TCL version 8.6
# gold on TCL WIKI, 30apr2021
package require Tk
package require math::numtheory
namespace path {::tcl::mathop ::tcl::mathfunc math::numtheory }
set tcl_precision 17
frame .frame -relief flat -bg aquamarine4
pack .frame -side top -fill y -anchor center
set names {{} {initial seed event, in human age ,decimal years with decimal fraction :} }
lappend names {reference year, usually birth year with decimal fraction: }
lappend names {optional switch mode, usually 1 for no decay, decay modes = 2, 3, 4: }
lappend names {optional constant in decay mode, nominal 1 : }
lappend names {answers, probable 2nd next occurrence, decimal years : }
lappend names {probable 3 next occurrence, decimal years : }
lappend names {probable 4 next occurrence, decimal years : }
lappend names {probable 5 next occurrence, decimal years : }
lappend names {probable 6 next occurrence, decimal years : }
foreach i {1 2 3 4 5 6 7 8 9} {
label .frame.label$i -text [lindex $names $i] -anchor e
entry .frame.entry$i -width 35 -textvariable side$i
grid .frame.label$i .frame.entry$i -sticky ew -pady 2 -padx 1 }
proc about {} {
set msg "Calculator for Time Fractal Proportions V2
from TCL WIKI,
written on TCL 8.6 "
tk_messageBox -title "About" -message $msg }
proc self_help {} {
set msg "Calculator for Time Fractal Proportions V2
from TCL ,
# self help listing
# 1 given follow.
1) initial age decimal years N1
2) reference year or birth year
3) optional switch mode, usually 1 for no decay
# optional decay modes = 2, 3, 4, experimental use
4) optional variable decay constant, not used now
# This calculator uses golden ratio proportions
# to predict successive time windows or time fractals
# of similar probable occurrences based
# a seed time or initial age decimal years.
# There is plenty of uncertainty about probable occurrences
# and events after the seed time, but the
# the probable occurrences are largely based on growth,
# accumulation, and succession
# following the golden ratio proportions.
# Not all events in time have golden ratio proportions.
# optional switch mode, usually 1 for no decay,
# optional decay modes = 2, 3, 4
# experimental constant_k1 reduces later
# time waves in length after 1st occurence
# setting _k1 decay factor and foreshortening set
# on time waves, called quickening
# but acceleration of events to person as observer on timeline.
# optional rise modes = -2, -3, -4
# setting _k1 rise factor and extra length set on time waves,
# but deacceleration of events to person as observer on timeline.
# not used & open yet, optional constant in decay mode, nominal 1
# For comparison, TCL code may include redundant paths & formulas.
# The TCL calculator normally uses modern
# units for convenience to modern users and textbooks.
# Any convenient and consistent in/output units might be used
# like inches, feet, nindas, cubits, or dollars to donuts.
# Recommended procedure is push testcase and fill frame,
# change first three entries etc, push solve,
# and then push report. Report allows copy and paste
# from console to conventional texteditor. For testcases
# testcase number is internal to the calculator and
# will not be printed until the report button is pushed
# for the current result numbers.
# Use one line errorx proc to estimate percent errors.
# errorx proc is used in the report window (console).
# Additional significant figures are used to check
# the TCL program, not to infer the accuracy
# of inputs and product reports.
# Proc precisionx <AM> is loaded and may be used to
# trim lengthy mantissas.
# precisionx used on select numbers only, not used on every number.
# On variable_cycle, may have to >> exit << to clear registers
# Conventional text editor formulas or grabbed from internet
# Screens can be pasted into green report console.
# Try copy and paste following into green screen console
# set answer \[* 1. 2. 3. 4. 5. \]
# returns 120
# gold on TCL Club, 30apr2021 "
tk_messageBox -title "self_help" -message $msg }
proc precisionx {precision float} {
# tcl:wiki:Floating-point formatting, <AM>
# select numbers only, not used on every number.
set x [ expr {round( 10 ** $precision * $float) / (10.0 ** $precision)} ]
# rounded or clipped to nearest 7nd significant figure
set x [ format "%#.7g" $x ]
return $x
}
proc time_fractal {age_years} {
set g_constant .6180339887498948420
# golden ratio is 1.6180339887498948420
set year_occurrence [ expr { $age_years + $g_constant * $age_years } ]
return $year_occurrence
}
# Use one line errorx proc to estimate percent errors
# errorx proc is used in the report window (console)
proc errorx {aa bb} {expr { $aa > $bb ? (($aa*1.)/$bb -1.)*100. : (($bb*1.)/$aa -1.)*100.}}
proc reverse_time_fractal {age_years} {
set g_constant 1.61803398874989484820
set reverse_time_fractal [ expr { $age_years * (1./$g_constant) } ]
# return $reverse_fractal
}
# variable_cycle proc is referenced to calendar years CE
# start test one line procedure for variable_cycle proc
set seed_date 1941.12
set yearx [ expr { ($seed_date + 3113.) + ((5125.-($seed_date + 3113.))*.618*(($seed_date + 3113.)/5125.))-3113. } ]
proc variable_cycle { mayan_cycle seed_date } {expr { ($seed_date + 3113.) + (($mayan_cycle-($seed_date + 3113.))*.618*(($seed_date + 3113.)/$mayan_cycle))-3113. } }
proc variable_function { seed_date cycles_needed } {
set tcl_precision 17
set counter 0
set result { list }
set mayan_cycle 5125.
set precessional_cycle 25625.
# expr { 25625./5125 } # returns 5.0
set mayan_cycle 5125.
# if seed_date approaches 2012 or end of mayan_cycle 5125,
# one might increase mayan_cycle to avoid asymptotic.
# if { $seed_date > 1992.} { set mayan_cycle 5175.}
lappend result { list $seed_date }
lappend result [precisionx 7 [ variable_cycle $mayan_cycle $seed_date ]]
set result1 [ variable_cycle $mayan_cycle $seed_date ]
while { $counter < 50. } {
lappend result_list $result1
set result1 [precisionx 7 [ variable_cycle $mayan_cycle $result1 ]]
if { $counter > $cycles_needed } {break}
incr counter
}
set seed_date 0 ;return $result_list }
proc study_initial_conditions {} {
global answer2
global side1 side2 side3 side4 side5
global side6 side7 side8 side9
global side10 side11 side12
global g_constant gr age_years reference_year
global testcase_number golden_time_cycle
global option_mode optional_constant seed_date
# start study of initial conditions on seed event
puts "start study of initial conditions "
if { [abs $side3] > 1. } { puts " ************************* "}
if { [abs $side3] > 1. } { puts " variable_wave_reduction in effect "}
if { [abs $side3] > 1. } { puts " ************************* "}
set street_life_male_avg [list 0.0000001 13. 18. 21. 24. 29.8 36.5 43.5 55. 60. 65. 73.]
foreach item $street_life_male_avg {lappend street_life_male_avg_gregorian [ precisionx 7 [+ $item $side2 ]] }
# reverse operation is of interest in
# observer problem finding seed event value if unknown
puts "observer value $age_years returns prior reverse"
puts "returns prior reverse [reverse_time_fractal $age_years] "
puts "prior reverse rnd [ precisionx 6 [reverse_time_fractal $age_years]] "
puts " seed event rounded [precisionx 5 $age_years ] "
puts " estimated golden_time_cycle rounded [precisionx 5 $golden_time_cycle ] "
puts "end study of initial conditions "
set real_scaled_results [list 0.000001 $side1 $side5 $side6 $side7 $side8 $side9 $side10 $side11]
puts " output set of results in years $real_scaled_results "
foreach item $real_scaled_results {lappend rnd_scaled_results [ precisionx 5 $item ] }
foreach item $real_scaled_results {lappend rnd_scaled_gregorian_results [ precisionx 7 [+ $item $side2 ]] }
puts " output street_life_male_avg in human age years $street_life_male_avg "
puts " output rounded set of results in years $rnd_scaled_results "
puts " output street_life_male_avg in gregorian years $street_life_male_avg_gregorian "
puts " output rounded set of results in gregorian years $rnd_scaled_gregorian_results "
# variable_cycle proc is referenced to calendar years CE
# example use of variable_cycle proc
# reporting test use first
puts "******************* "
puts "******* Test variable_cycle proc************ "
puts "test3 seed_date= $seed_date, 10 waves, list of results [ variable_function $seed_date 10 ] "
puts " may have to >> exit << to clear registers on variable_cycle "
puts " end of variable_cycle test, seed_date= $seed_date"
}
proc calculate { } {
global answer2
global side1 side2 side3 side4 side5
global side6 side7 side8 side9
global side10 side11 side12
global g_constant gr age_years reference_year
global testcase_number golden_time_cycle
global option_mode optional_constant seed_date
incr testcase_number
set side1 [* $side1 1. ]
set side2 [* $side2 1. ]
set side3 [* $side3 1. ]
set side4 [* $side4 1. ]
set side10 1.
set side11 1.
set side12 1.
set age_years [ expr { $side1*1.0 } ]
set reference_year [ expr { $side2*1.0 } ]
set option_mode [ expr { $side3*1.0 } ]
set optional_constant [ expr { $side4*1.0 } ]
set seed_date [ expr { $side1 + $side2 } ]
# golden conjugate is 0.61803398874989484820
# alternate test value for
# golden conjugate is 0.618
# but do not see much difference on small numbers
# under 20
# initialize golden ratio constants
set gr 1.61803398874989484820
set g_constant 0.61803398874989484820
set year_occurrence [ time_fractal $age_years ]
set golden_time_cycle [ expr { $year_occurrence - $age_years } ]
# experimental constant_k1 reduces later
# time waves in length after 1st occurence
set constant_k1 1.
# setting for constant length time waves
if { $side3 == 1. } {set constant_k1 1. }
# decay factor and foreshortening set on time waves, called quickening
# but acceleration of events to person as observer on timeline.
if { $side3 > 1. } {set constant_k1 [ expr { 1. * exp(-.1* $side3)} ]}
# rise factor and extra length set on time waves,
# but deacceleration of events to person as observer on timeline.
if { $side3 < 1. } {set constant_k1 [ expr { 1. * exp(-.1* $side3)} ]}
set side12 $constant_k1
set side5 [ expr { $age_years + $golden_time_cycle * 1. } ]
set side6 [ expr { $age_years + 2 * $golden_time_cycle * $constant_k1 } ]
set side7 [ expr { $age_years + 3 * $golden_time_cycle * $constant_k1 } ]
set side8 [ expr { $age_years + 4 * $golden_time_cycle * $constant_k1 } ]
set side9 [ expr { $age_years + 5 * $golden_time_cycle * $constant_k1 } ]
set side10 [ expr { $age_years + 6 * $golden_time_cycle * $constant_k1 } ]
set side11 [ expr { $age_years + 7 * $golden_time_cycle * $constant_k1 } ]
# we have computed the set of constant golden waves
# link to proc for study of initial conditions
study_initial_conditions
}
proc fillup {aa bb cc dd ee ff gg hh ii} {
.frame.entry1 insert 0 "$aa"
.frame.entry2 insert 0 "$bb"
.frame.entry3 insert 0 "$cc"
.frame.entry4 insert 0 "$dd"
.frame.entry5 insert 0 "$ee"
.frame.entry6 insert 0 "$ff"
.frame.entry7 insert 0 "$gg"
.frame.entry8 insert 0 "$hh"
.frame.entry9 insert 0 "$ii"
}
proc clearx {} {
foreach i {1 2 3 4 5 6 7 8 9 } {
.frame.entry$i delete 0 end } }
proc reportx {} {
global side1 side2 side3 side4 side5
global side6 side7 side8 side9 gr
global side10 side11 side12
global testcase_number golden_time_cycle
global g_constant gr age_years reference_year
global option_mode optional_constant
console show;
puts "%|table $testcase_number| || printed in tcl wiki format|% "
puts "&| quantity| value years |years CE| comment, if any|& "
puts "&| $testcase_number:|testcase_number || |&"
puts "&| $side1 :|initial seed year, human age, decimal years with decimal fraction | | |&"
puts "&| $side2 :|reference year, birth year, decimal years with decimal fraction : | | |& "
puts "&| $side3 :|option switch mode, usually 1 for no decay, decay modes = 2, 3, 4: | | |& "
puts "&| $side4 :|optional constant in decay mode, nominal 1 :: | | |& "
puts "&| $golden_time_cycle :|estimated golden_time_cycle, decimal years with decimal fraction : | | |& "
puts "&| $side12 :| experimental decay constant_K1 : | | |& "
puts "&| Note :| experimental constant_k1 reduces later time waves after 1st occurance : | | |& "
puts "&| $side1 :|initial seed year, first occurrence, decimal years : |[+ $side1 $side2 ] | |& "
puts "&| $side5 :|probable 2 next occurrence, decimal years : |[+ $side5 $side2 ] | |& "
puts "&| $side6 :|probable 3 next occurrence, decimal years : |[+ $side6 $side2 ] | |& "
puts "&| $side7 :|probable 4 next occurrence, decimal years : |[+ $side7 $side2 ] | |&"
puts "&| $side8 :|probable 5 next occurrence, decimal years : |[+ $side8 $side2 ] | |&"
puts "&| $side9 :|probable 6 next occurrence, decimal years : |[+ $side9 $side2 ] | |&"
puts "&| $side10 :|probable 7 next occurrence, decimal years : | [+ $side10 $side2 ] | |&"
puts "&| $side11 :|probable 8 next occurrence, decimal years : | [+ $side11 $side2 ] | |&"
}
frame .buttons -bg aquamarine4
::ttk::button .calculator -text "Solve" -command { calculate }
::ttk::button .test2 -text "Testcase1" -command {clearx;fillup 11. 1980. 1. 1. 17.79 24.59 31.39 38.19 44.99 }
::ttk::button .test3 -text "Testcase2" -command {clearx;fillup 10.0 1900. 1. 1. 16.18 22.36 28.54 34.72 42.360 }
::ttk::button .test4 -text "Testcase3" -command {clearx;fillup 13.195 1980.508 1. 1. 21.35 29.5 37.66 45.81 53.97}
::ttk::button .clearallx -text clear -command {clearx }
::ttk::button .about -text about -command {about}
::ttk::button .self_help -text self_help -command {self_help }
::ttk::button .cons -text report -command { reportx }
::ttk::button .exit -text exit -command {exit}
pack .calculator -in .buttons -side top -padx 10 -pady 5
pack .clearallx .cons .self_help .about .exit .test4 .test3 .test2 -side bottom -in .buttons
grid .frame .buttons -sticky ns -pady {0 10}
. configure -background aquamarine4 -highlightcolor brown -relief raised -border 30
wm title . "Time Fractal Proportions Calculator V2 "
# end of working deck
# add cosmetics below to bottom of file
console eval {.console config -bg palegreen}
console eval {.console config -font {fixed 20 bold}}
console eval {wm geometry . 40x20}
console eval {wm title . " Report for Time Fractal Proportions Calculator V2 "}
console eval {. configure -background orange -highlightcolor brown -relief raised -border 30}
puts " Console wrapper for solution proc"
puts " ***************************"
puts " ***************************" Hidden Comments Section
Please place any comments here, Thanks, gold 30Apr2021
gold 9/27/2021. Switched some comment signs ;# to #. This a big file. Check earlier editions, if not compatible. Maybe obvious that this code is PC based, not Unix, but this page was written on Windows10 Tcl ports including ActiveTCL. Not planning on writing Unix code. I assume reader can cut and paste on screen, what the reader needs, and tootle on to his own UNIX project and own contribution pages to the TCL Wiki.
x
| Category Numerical Analysis | Category Toys | Category Calculator | Category Mathematics | Category Example | Toys and Games | Category Games | Category Application | Category GUI |