Koch Snowflake Modeling Growth and TCL demo example calculator, numerical analysis
Koch Snowflake Modeling Growth and TCL demo example calculator, numerical analysis V2
This page is under development. Comments are welcome, but please load any comments in the comments section at the bottom of the page. Please include your wiki MONIKER and date in your comment with the same courtesy that I will give you. Aside from your courtesy, your wiki MONIKER and date as a signature and minimal good faith of any internet post are the rules of this TCL-WIKI. Its very hard to reply reasonably without some background of the correspondent on his WIKI bio page. Thanks, gold 20Aug2021
- Koch Snowflake Modeling Growth and TCL demo example calculator, numerical analysis V2
- Preface
- Introduction
- Fractal Limits of the simulated reality from Koch snowflake modeling growth
- Considerations for Koch Snowflake into TCL code
- The Fractal Code of Simulated Reality and the Limitations of Growth
- Pushbutton Operation
- Conclusions
- References:
- Screenshots Section
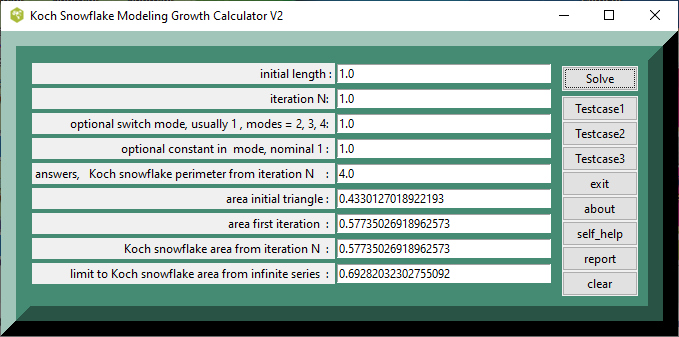
- figure 1a.Screenshot, Koch_Snowflake_Modeling_Growth_screenshot
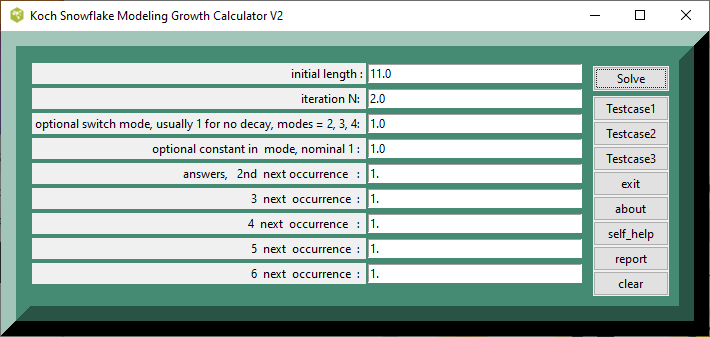
- figure 1b. Initial Vaporware screenshot, Koch_Snowflake_Modeling_Growth_screenshot
- figure 2. report_card,Koch_Snowflake_Modeling_Growth_report
- figure 3. Credit. wikipedia/commons/,Koch_Snowflake_Modeling_Growth_patternx
- figure 4. Credit. wikipedia/commons/, Koch_Snowflake_Modeling_Growth_patterns
- figure 5. Credit Romero Schmidtke on es.wikipedia/commons, Koch_Snowflake_Modeling_Growth_flake
- figure 6. Credit. wikipedia/commons/f/f0/Flocke.PNG, Koch_Snowflake_Modeling_Growth_pattern_more
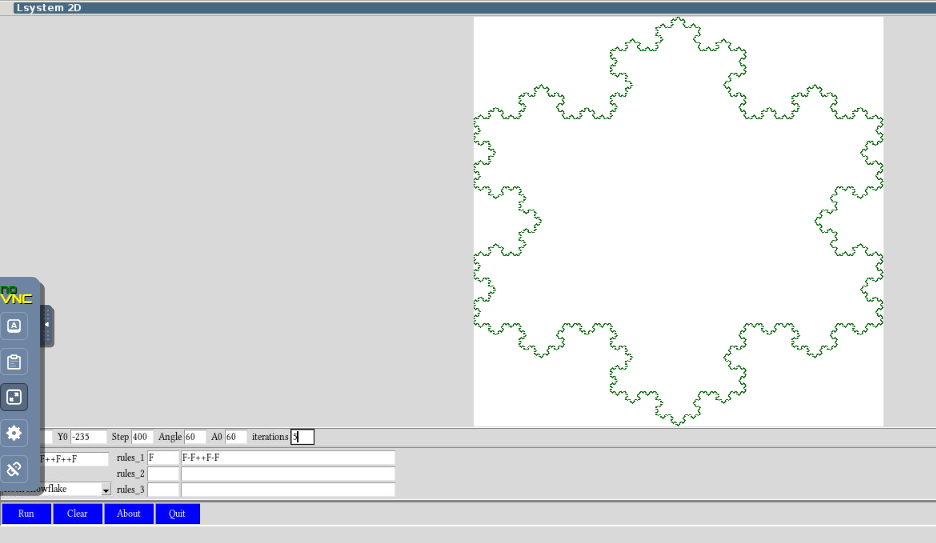
- figure 7. Credit. L-system 2D on TCL wiki GS, Koch_Snowflake_Modeling_Growth_pattern_more
- figure 8. Credit. onlinefractaltools.com/draw-koch-fractal, Koch_Snowflake_Modeling_Growth_flake_brown
- figure 9. Credit. onlinefractaltools.com/draw-koch-fractal, Koch_Snowflake_Modeling_Growth_flake_brown_2
- figure 10. Credit. opentextbc.ca/calculusv2openstax, Koch_Snowflake_Modeling_Growth_koch_snowflake_
- figure 11. Credit. Thomas Hertog universe big bang time , Koch_Snowflake_Modeling_Growth_big bang_
- figure 11b. Credit. Thomas Hertog universe big bang time , Koch Snowflake Modeling Growth, radiation map #2
- figure 12. Credit. Thomas Hertog universe big bang time , Koch Snowflake Modeling Growth, universe model of time
- figure 14. Credit. Thomas Hertog universe big bang time , Koch Snowflake Modeling Growth book cover2
- Testcases Section
- Feedback from X-Non
- Hidden Comments Section
- Categories Section
Preface
gold 15aug2021 Here are some calculations for Koch Snowflake Modeling Growth. High school geometry class was to the rescue on constructing the Universe From scratch, Bruce Camber,2016,. Note. When I started this page, I did not know about L-system 2D on this TCL wiki, but still think I could learn some. Strange that some search engines are not pulling this remarkable page L-system 2D on this wiki.
Introduction
Fractal Limits of the simulated reality from Koch snowflake modeling growth
Fractal Code of the simulated reality is similar to repetitive patters in our lives, per lecture of Gregg Braden. Repetitive patterns in our lives hows fractal growth is limited. Koch snowflake. Area or growing curve of Koch snowflake has 1.6X limit. Koch snowflake has 1.6X limit to area growth of fractal pattern. First area increase of Koch snowflake is 1/3, 2nd iteration is 4/27, 3ird iteration is 16/243, 4th iteration is 64/2187. The area limit is 1.6X. Perimeter or edge of fractal simulation can change to infinite complexity. How long fractal pattern or simulation lasts? How complex edge or perimeter can become? The limiting scale of universe may called the Planck length, which means there may be a limit to how large the universe may become, quoting Steven Hawking.
Alternate Gist. The Fractal Code of the simulated reality can be compared to the repetitive patterns in our lives, as suggested by Gregg Braden's lecture. These patterns can be observed in nature, such as the Koch snowflake, which demonstrates a fractal growth with a 1.6X limit to its area growth. The area growth of the Koch snowflake follows a specific pattern with increasing iterations: 1/3, 4/27, 16/243, and 64/2187 for the first four iterations. The perimeter or edge of the fractal simulation can change to infinite complexity, meaning that the pattern can continue to develop and evolve without any apparent limit. However, the possible limiting scale factor of the universe, known as the Planck length, suggests that there may be a limit to how large the universe can become. This concept was supported by theoretical physicist, the late Stephen Hawking. In summary, the Fractal Code of the simulated reality can be observed in patterns like the Koch snowflake, which has a 1.6X limit to its area growth. The perimeter or edge of the fractal simulation can become infinitely complex, while the Planck length may serve as a limit to the size of the universe.
Considerations for Koch Snowflake into TCL code
Most of the online references are calculating the area ratio of the Koch_snowflake to the initial equilateral triangle of side 1. The TCL calculator was calculating the area of the Koch_Snowflake per se. Its a little difficult to find reference testcases or spreadsheets of the Koch_Snowflake_Area(N) to check my area proc and printout in TCL.
The Fractal Code of Simulated Reality and the Limitations of Growth
Gregg Braden's lecture on the fractal code of simulated reality highlights the repetitive patterns found in our lives, much like the growth patterns observed in fractal geometry. One such fractal pattern is the Koch snowflake, which demonstrates a fascinating characteristic: a limit to its area growth. This limit is set at 1.6 times the initial area, and it can be observed through the iterative process of the snowflake's construction. The area growth of the Koch snowflake follows a specific pattern: 1/3, 4/27, 16/243, and 64/2187 for the first four iterations. As the iterations continue, the area grows exponentially, but it eventually reaches a limit at 1.6 times the initial area.
This limitation in area growth is a direct result of the fractal nature of the Koch snowflake. In contrast, the perimeter or edge of a fractal simulation can become infinitely complex. The complexity of the edge or perimeter can continue to grow as the fractal pattern unfolds, with no inherent limit to its complexity. This characteristic of fractal geometry is one of the reasons why fractals are so intriguing and visually striking.
The concept of a limiting scale in the universe, such as the Planck length, as mentioned by Steven Hawking, suggests that there may be a limit to how large the universe can become. This idea is similar to the limitation of area growth observed in the Koch snowflake, as both suggest that there is a boundary or constraint to the size and complexity of a system or pattern. In conclusion, the fractal code of simulated reality and the limitations of growth observed in patterns like the Koch snowflake provide valuable insights into the nature of complex systems and their inherent constraints. As we continue to explore and understand these patterns, we may uncover deeper connections between the microcosm and the macrocosm, revealing the fractal nature of the universe itself.
Pushbutton Operation
For the push buttons, the recommended procedure is push testcase and fill frame, change first three entries etc, push solve, and then push report. Report allows copy and paste from console. For testcases in a computer session, the eTCL calculator increments a new testcase number internally, eg. TC(1), TC(2) , TC(3) , TC(N). The testcase number is internal to the calculator and will not be printed until the report button is pushed for the current result numbers. The current result numbers will be cleared either on the next clear button or on the next solve button. All results will be lost on program exit, unless the report text is saved from the report screen on console.
Conclusions
The perimeter calculations were accurate. Proc :math::snowflake_area needs some work and check on upper bounds of operation.
References:
- Wikipedia search engine < Mandelbrot >
- Wikipedia search engine < Koch >
- Wikipedia search engine < Programming Examples >
- Google search engine < Koch >
- Google search engine < Koch snowflake >
- Book >>
- One Liners Programs Pie in the Sky
- One Liners
- One Liners Programs Compendium [L1 ]
- WIKI BOOKS, Programming_Examples pdf
- WIKI BOOKS, Tcl_Programming_Introduction pdf
- google search engine < Koch snowflake>
- podcast/2021/08/02/158-david-wallace-on-the-arrow-of-time
- Video :Gregg Braden - Fractal Code of the Simulated Reality
- = Repetitive Patters in Our Lives
- shows fractal limit, growing curve of growing snowflake, 1.6X limit
- Planck length, en.wikipedia.org/wiki/Stephen_Hawking
- High School geometry class to the rescue.
- On Constructing the Universe From Scratch
- JANUARY 8, 2016, Bruce Camber
- bblu.org/2016/01/08/number
- A mathematical analysis of the Koch curve and quadratic Koch curve, pdf
- rosettacode.org/wiki/Koch_curve
- L-system 2D,GS (20100606), wfr.tcl-lang.org/1808, TCL code on fractals
- L-system 2D , GS lsystem2d.tcl, Author: Gerard Sookahet
- Artificial life
- Life
- code.activestate.com/recipes
- MANDELBROT FRACTAL IMAGE OUTPUT TO PPM FILE (PYTHON RECIPE)
- Modeling Planetary Distances using Titius-Bode Law and and TCL demo example calculator, numerical analysis V2
- Time Fractals in Golden Ratio Proportions and TCL demo example calculator, numerical analysis
- Text Adventure Game and TCL Demo Example [L2 ]
- Parametric Equation Model Vaporware TCL calculator [L3 ]
- One Liners Programs Compendium and TCL demo examples calculations, numerical analysis [L4 ]
- Basic_RS V2 in TCL as partial Basic language interpreter ed
- HgA1c Approximates Average Blood Glucose in Console Example Demo for TCL table format V2 [L5 ]
- Babylonian Expansion Procedure Algorithm and demo example calculator, numerical analysis [L6 ]
- Koch Snowflake and Sierpinski Triangle Combination Fractal « Python recipes
- Colouring graphs
- Pascal's triangle
- Mandelbrot and Julia sets
- Manipulating infinite sets in Tcl
- Manipulating sets in Tcl
- sergiol codegolf.stackexchange.com/a/113329/29325 unintentionally beautiful:
- mandelbrot-image-in-every-language/ *
- Tcl/Tk, 316, Shorter version using 3 letter #RGB shorthands style color
- sergiol triplets (instead of #RRGGBB triplets), which results in different colors.
- maybe codegolf Tcl/Tk _316 could be blended into [L7 ]
- www.wolframalpha.com input/?i=koch+snowflake+4
- Calculating Space, Konrad Zuse
- The Computer: My Life, Zuse, Konrad
- www.greggbraden.com/living-in-a-virtual-simulation/
Screenshots Section
figure 1a.Screenshot, Koch_Snowflake_Modeling_Growth_screenshot
figure 1b. Initial Vaporware screenshot, Koch_Snowflake_Modeling_Growth_screenshot
figure 2. report_card,Koch_Snowflake_Modeling_Growth_report
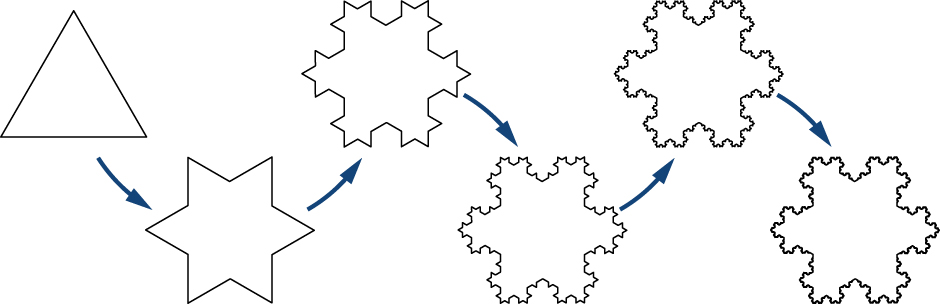
figure 3. Credit. wikipedia/commons/,Koch_Snowflake_Modeling_Growth_patternx
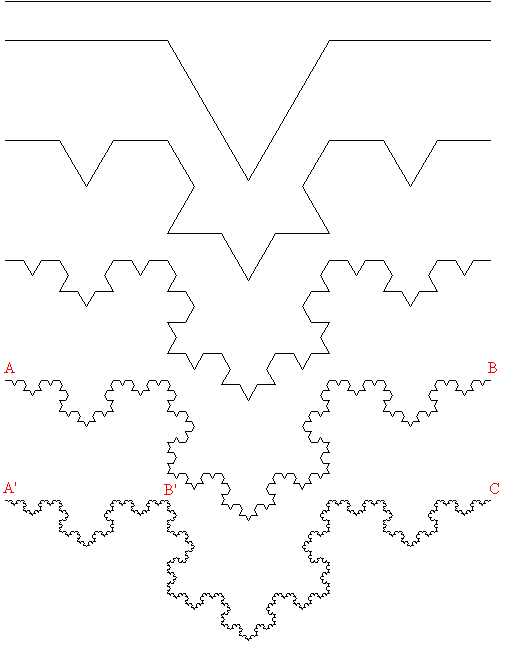
figure 4. Credit. wikipedia/commons/, Koch_Snowflake_Modeling_Growth_patterns
figure 5. Credit Romero Schmidtke on es.wikipedia/commons, Koch_Snowflake_Modeling_Growth_flake
figure 6. Credit. wikipedia/commons/f/f0/Flocke.PNG, Koch_Snowflake_Modeling_Growth_pattern_more
figure 7. Credit. L-system 2D on TCL wiki GS, Koch_Snowflake_Modeling_Growth_pattern_more
figure 8. Credit. onlinefractaltools.com/draw-koch-fractal, Koch_Snowflake_Modeling_Growth_flake_brown
figure 9. Credit. onlinefractaltools.com/draw-koch-fractal, Koch_Snowflake_Modeling_Growth_flake_brown_2
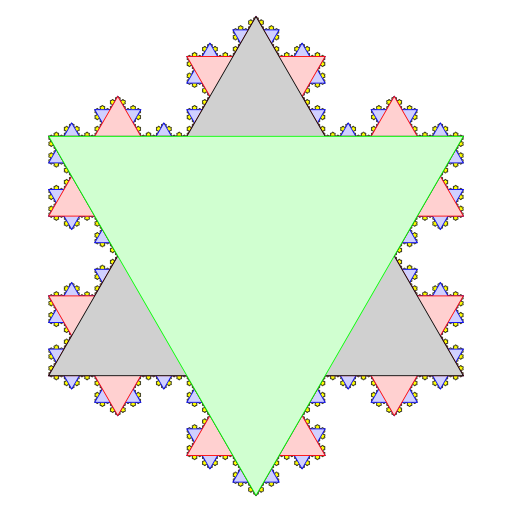
figure 10. Credit. opentextbc.ca/calculusv2openstax, Koch_Snowflake_Modeling_Growth_koch_snowflake_
---
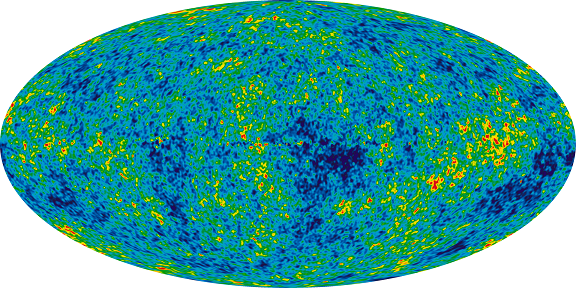
figure 11. Credit. Thomas Hertog universe big bang time , Koch_Snowflake_Modeling_Growth_big bang_
Recent map of cosmic radiation observed on earth satellite.
figure 11b. Credit. Thomas Hertog universe big bang time , Koch Snowflake Modeling Growth, radiation map #2
Thomas Hertog has presented several maps, cosmic radiation observed on earth satellite
---
figure 12. Credit. Thomas Hertog universe big bang time , Koch Snowflake Modeling Growth, universe model of time
Thomas Hertog has presented several maps and theories about the universe model of time. This map of Hertog Time model has close resemblance to the Koch Snowflake pattern. The Big Bang and early time is in the center of the diagram. The outer edge has more complexity, somewhat like the Koch Snowflake. Koch Snowflake Modeling Growth radiation map2
figure 14. Credit. Thomas Hertog universe big bang time , Koch Snowflake Modeling Growth book cover2
Thomas Hertog book cover. The Big Bang and early time is in the center of the diagram. The outer edge has more complexity, somewhat like the Koch Snowflake.
Testcases Section
In planning any software, it is advisable to gather a number of testcases to check the results of the program.
Testcase 1, Equilateral triangle of side length 1
Testcase 1. Equilateral triangle has side of length 1. The area of equilateral triangle is expr {1.*1.*1.732/4.}, 0.433. The snowflake formula is expr {(1.*1.*1.732*2) /5.}, 0.692799. Check: the ratio of the two areas approximates expr {0.692/.433}, ~1.598. The exact ratio is 1.6. TCL calculator returns 0.69282032302755092. The exact ratio expr {0.69282032302755092/0.4330127018922193}, returns 1.600000000000000.
| table 1 | printed in tcl wiki format | ||
|---|---|---|---|
| quantity | value | value | comment, if any |
| 1: | testcase_number | ||
| 1.0 : | initial length | ||
| 1.0 : | iteration : | ||
| 1.0 : | option switch mode, usually 1 , modes = 2, 3, 4: | ||
| 1.0 : | optional constant, nominal 1 :: | ||
| 1. : | experimental decay constant_K1 : | ||
| Note : | experimental constant_k1 not used : | ||
| 4.0 : | Koch snowflake perimeter from iteration N : | ||
| 0.4330127018922193 : | area initial triangle : | ||
| 0.57735026918962573 : | area first iteration : | ||
| 0.57735026918962573 : | Koch snowflake area from iteration N : | ||
| 0.69282032302755092 : | limit to Koch snowflake area from infinite series : |
Testcase 2.length 10
The snowflake starts with equilateral triangle, which has side of length 10. The TCL calculator returns snowflake area of 69.2820
| table 2 | printed in tcl wiki format | ||
|---|---|---|---|
| quantity | value | value | comment, if any |
| 2: | testcase_number | ||
| 10.0 : | initial length | ||
| 1.0 : | iteration : | ||
| 1.0 : | option switch mode, usually 1 , modes = 2, 3, 4: | ||
| 1.0 : | optional constant, nominal 1 :: | ||
| 1. : | experimental decay constant_K1 : | ||
| Note : | experimental constant_k1 not used : | ||
| 40.0 : | Koch snowflake perimeter from iteration N : | ||
| 43.301270189221931 : | area initial triangle : | ||
| 57.735026918962575 : | area first iteration : | ||
| 57.735026918962575 : | Koch snowflake area from iteration N : | ||
| 69.282032302755084 : | limit to Koch snowflake area from infinite series : |
Testcase 3.length 100
The snowflake starts with equilateral triangle, which has side of length 100. The TCL calculator returns snowflake area of 6928.2032.
| table 3 | printed in tcl wiki format | ||
|---|---|---|---|
| quantity | value | value | comment, if any |
| 3: | testcase_number | ||
| 100.0 : | initial length | ||
| 1.0 : | iteration : | ||
| 1.0 : | option switch mode, usually 1 , modes = 2, 3, 4: | ||
| 1.0 : | optional constant, nominal 1 :: | ||
| 1. : | experimental decay constant_K1 : | ||
| Note : | experimental constant_k1 not used : | ||
| 400.0 : | Koch snowflake perimeter from iteration N : | ||
| 4330.1270189221932 : | area initial triangle : | ||
| 5773.5026918962576 : | area first iteration : | ||
| 5773.5026918962576 : | Koch snowflake area from iteration N : | ||
| 6928.2032302755088 : | limit to Koch snowflake area from infinite series : |
Testcase 4. Koch_Snowflake_area(N)
The snowflake starts with initial equilateral triangle of sides = 1.
| Table Koch_Snowflake_Area(N) | with Snowflake_Perimeter(N) | ||||
|---|---|---|---|---|---|
| counter | Koch_Snowflake_Area(N) | Snowflake_Perimeter(N) | area ratio to initial triangle | area initial triangle | comment, if any |
| 0 | 0.4330127018922193 | 3.0 | 1.0 | 0.4330127018922193 | initial equilateral triangle of sides = 1. |
| 1 | 0.57735026918962584 | 4.0 | 1.3333333333333335 | 0.4330127018922193 | |
| 2 | 0.64150029909958417 | 5.333333333333333 | 1.4814814814814816 | 0.4330127018922193 | |
| 3 | 0.67001142350401022 | 7.1111111111111089 | 1.5473251028806587 | 0.4330127018922193 | |
| 4 | 0.68268303435042177 | 9.4814814814814792 | 1.5765889346136261 | 0.4330127018922193 | |
| 5 | 0.68831486139327125 | 12.641975308641971 | 1.5895950820505005 | 0.4330127018922193 | |
| 6 | 0.69081789563453777 | 16.855967078189295 | 1.5953755920224448 | 0.4330127018922193 | |
| 7 | 0.69193035529732283 | 22.474622770919058 | 1.5979447075655311 | 0.4330127018922193 | |
| 8 | 0.69242478181411626 | 29.966163694558741 | 1.5990865366957918 | 0.4330127018922193 | |
| 9 | 0.69264452693269107 | 39.954884926078321 | 1.5995940163092408 | 0.4330127018922193 | |
| 10 | 0.6927421914298354 | 53.273179901437764 | 1.599819562804107 | 0.4330127018922193 | |
| 11 | 0.69278559787301064 | 71.030906535250338 | 1.5999198056907142 | 0.4330127018922193 | |
| 12 | 0.69280488962553299 | 94.707875380333789 | 1.5999643580847618 | 0.4330127018922193 | |
| 13 | 0.6928134637377652 | 126.27716717377838 | 1.5999841591487831 | 0.4330127018922193 | |
| 14 | 0.69281727445431285 | 168.36955623170448 | 1.5999929596216815 | 0.4330127018922193 | |
| 15 | 0.69281896810611177 | 224.49274164227265 | 1.5999968709429695 | 0.4330127018922193 | |
| 16 | 0.69281972084024457 | 299.32365552303014 | 1.5999986093079863 | 0.4330127018922193 | |
| 17 | 0.69282005538874813 | 399.09820736404026 | 1.5999993819146607 | 0.4330127018922193 | |
| 18 | 0.69282020407697187 | 532.13094315205353 | 1.5999997252954048 | 0.4330127018922193 | |
| 19 | 0.69282027016062697 | 709.50792420273808 | 1.5999998779090689 | 0.4330127018922193 | |
| 20 | 0.69282029953114022 | 946.01056560365078 | 1.5999999457373639 | 0.4330127018922193 | |
| 21 | 0.69282031258470178 | 1261.3474208048674 | 1.599999975883273 | 0.4330127018922193 | |
| 22 | 0.69282031838628466 | 1681.7965610731567 | 1.5999999892814547 | 0.4330127018922193 | |
| 23 | 0.69282032096476598 | 2242.3954147642085 | 1.5999999952362023 | 0.4330127018922193 | |
| 24 | 0.6928203221107575 | 2989.8605530189443 | 1.5999999978827564 | 0.4330127018922193 | |
| 25 | 0.69282032262008719 | 3986.4807373585927 | 1.599999999059003 | 0.4330127018922193 | |
| 26 | 0.69282032284645589 | 5315.3076498114569 | 1.5999999995817791 | 0.4330127018922193 | |
| 27 | 0.69282032294706419 | 7087.0768664152747 | 1.5999999998141239 | 0.4330127018922193 | |
| 28 | 0.69282032299177909 | 9449.4358218870329 | 1.5999999999173886 | 0.4330127018922193 | |
| 29 | 0.69282032301165231 | 12599.247762516045 | 1.5999999999632839 | 0.4330127018922193 | |
| 30 | 0.69282032302048491 | 16798.997016688056 | 1.5999999999836818 | 0.4330127018922193 |
Math checks are from www.wolframalpha.com snowflake calculator. The snowflake starts with equilateral triangle of sides = 1. Most of the online references are calculating the area ratio of the Koch_snowflake to the initial equilateral triangle of side 1. The TCL calculator was calculating the area of the Koch_Snowflake per se.
Dimensions after 1 iteration length | 4 (times initial side length) area | 4/3 ≈ 1.33333 (times initial area) Dimensions after 2 iterations length | 16/3 ≈ 5.33333 (times initial side length) area | 40/27 ≈ 1.48148 (times initial area) Dimensions after 3 iterations length | 64/9 ≈ 7.11111 (times initial side length) area | 376/243 ≈ 1.54733 (times initial area) Dimensions after 4 iterations length | 256/27 ≈ 9.48148 (times initial side length) area | 3448/2187 ≈ 1.57659 (times initial area) Dimensions after 5 iterations length | 1024/81 ≈ 12.642 (times initial side length) area | 31288/19683 ≈ 1.5896 (times initial area)-
Appendix TCL programs and scripts
Pretty Print Version
# pretty print from autoindent and ased editor occurrence # Koch Snowflake Modeling Growth calculator # written on Windows 10 # working under TCL version 8.6 # gold on TCL WIKI, 19aug2021 package require Tk package require math::numtheory namespace path {::tcl::mathop ::tcl::mathfunc math::numtheory } set tcl_precision 17 frame .frame -relief flat -bg aquamarine4 pack .frame -side top -fill y -anchor center set names {{} {initial length :} } lappend names {iteration N: } lappend names {optional switch mode, usually 1 , modes = 2, 3, 4: } lappend names {optional constant in mode, nominal 1 : } lappend names {answers, Koch snowflake perimeter from iteration N : } lappend names { area initial triangle : } lappend names { area first iteration : } lappend names { Koch snowflake area from iteration N : } lappend names { limit to Koch snowflake area from infinite series : } foreach i {1 2 3 4 5 6 7 8 9} { label .frame.label$i -text [lindex $names $i] -anchor e entry .frame.entry$i -width 35 -textvariable side$i grid .frame.label$i .frame.entry$i -sticky ew -pady 2 -padx 1 } proc about {} { set msg "Calculator for Koch Snowflake Modeling Growth V2 from TCL WIKI, written on TCL 8.6 " tk_messageBox -title "About" -message $msg } proc self_help {} { set msg "Calculator for Koch Snowflake Modeling Growth V2 from TCL , # self help listing # 2 given follow. 1) initial length N1 2) iteration 3) optional switch mode, usually 1 for no decay # optional decay modes = 2, 3, 4, experimental use 4) optional variable decay constant, not used now # This calculator uses Koch snowflake proportions # based on initial length and iteration number # optional switch mode, usually 1 for no decay, # optional decay modes = 2, 3, 4 # experimental constant_k1 reduces later # optional rise modes = -2, -3, -4 # setting _k1 rise factor and extra length set on time waves, # but deacceleration of events to person as observer on timeline. # not used & open yet, optional constant in decay mode, nominal 1 # For comparison, TCL code may include redundant paths & formulas. # The TCL calculator normally uses modern # units for convenience to modern users and textbooks. # Any convenient and consistent in/output units might be used # like inches, feet, nindas, cubits, or dollars to donuts. # Recommended procedure is push testcase and fill frame, # change first three entries etc, push solve, # and then push report. Report allows copy and paste # from console to conventional texteditor. For testcases # testcase number is internal to the calculator and # will not be printed until the report button is pushed # for the current result numbers. # Use one line errorx proc to estimate percent errors. # errorx proc is used in the report window (console). # Additional significant figures are used to check # the TCL program, not to infer the accuracy # of inputs and product reports. # Proc precisionx <AM> is loaded and may be used to # trim lengthy mantissas. # precisionx used on select numbers only, not used on every number. # Conventional text editor formulas or grabbed from internet # Screens can be pasted into green report console. # Try copy and paste following into green screen console # set answer \[* 1. 2. 3. 4. 5. \] # returns 120 # gold on TCL Club, 30apr2021 " tk_messageBox -title "self_help" -message $msg } proc precisionx {precision float} { # tcl:wiki:Floating-point formatting, <AM> # select numbers only, not used on every number. set x [ expr {round( 10 ** $precision * $float) / (10.0 ** $precision)} ] # rounded or clipped to nearest 7nd significant figure set x [ format "%#.7g" $x ] return $x } # Use one line errorx proc to estimate percent errors # errorx proc is used in the report window (console) proc errorx {aa bb} {expr { $aa > $bb ? (($aa*1.)/$bb -1.)*100. : (($bb*1.)/$aa -1.)*100.}} # adapted from tcl-wiki Stats 2011-05-22, arithmetic mean [RLE] # # ::math::snowflake_area -- # # Return the division of quantity by two or more given ratios # # Arguments: # length first value is length # iteration second value is length # # Results: snowflake_area # proc ::math::snowflake_area {length iteration} { set area_eq_triangle [ expr { ($length*$length*sqrt(3.))/4.} ] set area_snowflake_nth [ expr { ($area_eq_triangle / 5.) * (8.-3.*(4./9.)**$iteration)}] return $area_snowflake_nth } proc calculate { } { global side1 side2 side3 side4 side5 global side6 side7 side8 side9 global side10 side11 side12 global g_constant gr age_years reference_year global testcase_number golden_time_cycle global option_mode optional_constant seed_date incr testcase_number set side1 [* $side1 1. ] set side2 [* $side2 1. ] set side3 [* $side3 1. ] set side4 [* $side4 1. ] set side9 1. set side10 1. set side11 1. set option_mode [ expr { $side3*1.0 } ] set optional_constant [ expr { $side4*1.0 } ] set seed_date [ expr { $side1 + $side2 } ] # golden conjugate is 0.61803398874989484820 # alternate test value for # golden conjugate is 0.618 # but do not see much difference on small numbers # under 20 # initialize golden ratio constants set gr 1.61803398874989484820 set g_constant 0.61803398874989484820 # experimental constant_k1 reduces later # time waves in length after 1st occurence set constant_k1 1. # setting if { $side3 == 1. } {set constant_k1 1. } set side12 $constant_k1 set length $side1 set iteration $side2 set area_initial_triangle [ expr { ($side1*$side1*sqrt(3.))/4.} ] set area_first_iteration [ expr { ($side1*$side1*sqrt(3.))/3.} ] set side6 $area_initial_triangle set side7 $area_first_iteration set koch_snowflake_perimeter [ expr { 3.*$side1*((4./3.)**$iteration)} ] # koch_snowflake_area is sum of infinite series of Nth areas set koch_snowflake_perimeter [ expr { 3.*$side1*((4./3.)**$iteration)} ] set side5 $koch_snowflake_perimeter set side8 [::math::snowflake_area $length $iteration] set koch_snowflake_area [ expr {(2.*$side1*$side1*sqrt(3.))/5.} ] set side9 $koch_snowflake_area # we have computed the set } proc fillup {aa bb cc dd ee ff gg hh ii} { .frame.entry1 insert 0 "$aa" .frame.entry2 insert 0 "$bb" .frame.entry3 insert 0 "$cc" .frame.entry4 insert 0 "$dd" .frame.entry5 insert 0 "$ee" .frame.entry6 insert 0 "$ff" .frame.entry7 insert 0 "$gg" .frame.entry8 insert 0 "$hh" .frame.entry9 insert 0 "$ii" } proc clearx {} { foreach i {1 2 3 4 5 6 7 8 9 } { .frame.entry$i delete 0 end } } proc reportx {} { global side1 side2 side3 side4 side5 global side6 side7 side8 side9 gr global side10 side11 side12 global testcase_number golden_time_cycle global g_constant gr age_years reference_year global option_mode optional_constant console show; puts "%|table $testcase_number| || printed in tcl wiki format|% " puts "&| quantity| value |value| comment, if any|& " puts "&| $testcase_number:|testcase_number || |&" puts "&| $side1 :|initial length | | |&" puts "&| $side2 :|iteration : | | |& " puts "&| $side3 :|option switch mode, usually 1 , modes = 2, 3, 4: | | |& " puts "&| $side4 :|optional constant, nominal 1 :: | | |& " puts "&| $side12 :| experimental decay constant_K1 : | | |& " puts "&| Note :| experimental constant_k1 not used : | | |& " puts "&| $side5 :| Koch snowflake perimeter from iteration N : | | |& " puts "&| $side6 :| area initial triangle : | | |& " puts "&| $side7 :| area first iteration : | | |&" puts "&| $side8 :| Koch snowflake area from iteration N : | | |&" puts "&| $side9 :| limit to Koch snowflake area from infinite series : | | |&" } frame .buttons -bg aquamarine4 ::ttk::button .calculator -text "Solve" -command { calculate } ::ttk::button .test2 -text "Testcase1" -command {clearx;fillup 1. 2. 1. 1. 5.33 0.433 0.577 5.33 0.69 } ::ttk::button .test3 -text "Testcase2" -command {clearx;fillup 1. 3. 1. 1. 7.11 0.433 0.577 7.11 0.69 } ::ttk::button .test4 -text "Testcase3" -command {clearx;fillup 1. 4. 1. 1. 9.48 0.433 0.577 9.48 0.69} ::ttk::button .clearallx -text clear -command {clearx } ::ttk::button .about -text about -command {about} ::ttk::button .self_help -text self_help -command {self_help } ::ttk::button .cons -text report -command { reportx } ::ttk::button .exit -text exit -command {exit} pack .calculator -in .buttons -side top -padx 10 -pady 5 pack .clearallx .cons .self_help .about .exit .test4 .test3 .test2 -side bottom -in .buttons grid .frame .buttons -sticky ns -pady {0 10} . configure -background aquamarine4 -highlightcolor brown -relief raised -border 30 wm title . "Koch Snowflake Modeling Growth Calculator V2 " # end of working deck # add cosmetics below to bottom of file console eval {.console config -bg palegreen} console eval {.console config -font {fixed 20 bold}} console eval {wm geometry . 40x20} console eval {wm title . " Report for Koch Snowflake Modeling Growth Calculator V2 "} console eval {. configure -background orange -highlightcolor brown -relief raised -border 30} puts " Console wrapper for solution proc" puts " ***************************" puts " ***************************"
Table for Koch_Snowflake_Area(N)
# pretty print from autoindent and ased editor occurrence # Koch Snowflake Modeling Growth table # written on Windows 10 ActiveTcl # working under TCL version 8.6 # gold on TCL WIKI, 19aug2021 package require Tk package require math::numtheory namespace path {::tcl::mathop ::tcl::mathfunc math::numtheory } console show set tcl_precision 17 puts " Console wrapper for solution proc" puts " ***************************" puts " ***************************" # ::math::snowflake_area -- # # Return the division of quantity by two or more given ratios # # Arguments: # length first value is length # iteration second value is length # # Results: snowflake_area # proc koch_snowflake_perimeter { side1 iteration } {return [ expr { 3.*$side1*((4./3.)**$iteration)}] } proc ::math::snowflake_area {length iteration} { set area_eq_triangle [ expr { ($length*$length*sqrt(3.))/4.} ] set area_snowflake_nth [ expr { ($area_eq_triangle / 5.) * (8.-3.*(4./9.)**$iteration)}] return $area_snowflake_nth } proc precisionx {precision float} { # tcl:wiki:Floating-point formatting, <AM> # select numbers only, not used on every number. set x [ expr {round( 10 ** $precision * $float) / (10.0 ** $precision)} ] # rounded or clipped to nearest 7nd significant figure set x [ format "%#.9g" $x ] return $x} proc expansion { length } { set counter -1 puts "%| Table Koch_Snowflake_Area(N)|with Snowflake_Perimeter(N) |||||% " puts "&| counter | Koch_Snowflake_Area(N) | Snowflake_Perimeter(N) | area ratio to initial triangle| area initial triangle | comment, if any |& " while { $counter < 30. } { incr counter puts "&| $counter | [::math::snowflake_area 1 $counter] | [ koch_snowflake_perimeter 1 $counter] | [/ [::math::snowflake_area 1 $counter] [::math::snowflake_area 1. 0] ] | [::math::snowflake_area 1. 0] | |& " } } # printout follows expansion 1 # end of working deck # add cosmetics below to bottom of file console eval {.console config -bg palegreen} console eval {.console config -font {fixed 20 bold}} console eval {wm geometry . 40x20} console eval {wm title . " Report for Koch Snowflake Modeling Growth Calculator V2 "} console eval {. configure -background orange -highlightcolor brown -relief raised -border 30}
gold 8/20/2021. Fractal geometry updates to Compendium
proc koch_snowflake_perimeter { side1 iteration } {return [ expr { 3.*$side1*((4./3.)**$iteration)}] } # Usage using set answer set answer3 [ koch_snowflake_perimeter 1. 5. ] proc area_eq_triangle { length } { return [ expr { ($length*$length*sqrt(3.))/4.} ] } # area_eq_triangle has to be initial triangle of length XX, if not equilateral triangle of 1. # Usage using set answer set area_eq_triangle [ area_eq_triangle 1. ] proc koch_snowflake_nth { iteration area_eq_triangle } {return [ expr { ($area_eq_triangle / 5.) * (8.-3.*(4./9.)**$iteration)}]} # Usage using set answer set area_eq_triangle [ area_eq_triangle 2. ] ;# answer = 1.7320508075688772 set answer2 [ koch_snowflake_nth 1 $area_eq_triangle ] ;# answer2 = 2.3094010767585034
gold 9/6/2023. We have received substantial feedback from X-Non. Thanks to X-Non. I think your comments add a lot. I tend to be very dry or else nobody understands my attempts at Jokes. Thank you again.
Feedback from X-Non
X-Non circa 9/6/2023
Okay, imagine you're drawing a snowflake with a piece of string. First, you make a small triangle. Then, on each side of that triangle, you add a smaller triangle. You keep doing this, adding even tinier triangles to the sides of the smaller triangles. This is called a Koch snowflake!
Now, let's talk about the string you're using. Even though you keep adding more and more tiny triangles, you'll notice that you can't make the snowflake super, super big. It can only get a little bit bigger each time you add more triangles. This is what we mean when we say the snowflake has a "1.6X limit to area growth."
But guess what? The string you're using to outline the snowflake can get super, super long! It can twist and turn in all sorts of ways, making the edge of your snowflake really complicated. That's what we mean when we say the "edge can become infinitely complex."
Just like your snowflake, the universe might have a limit on how big it can get. Some really smart people, like Steven Hawking, think there might be a smallest size anything can be, called the "Planck length," and that might limit how big the whole universe can get.
So, your snowflake is like a tiny model of the universe! Isn't that cool?
Hidden Comments Section
Please include your wiki MONIKER and date in your comment with the same courtesy that I will give you. Thanks, gold 12Aug2021
gold 9/27/2021. Switched some comment signs ;# to #. This a big file. Check earlier editions, if not compatible. Maybe obvious, but this page was written on Windows10 Tcl ports including ActiveTCL. I assume reader can cut and paste on screen, what the reader needs, and tootle on to his own project and own contribution pages to the TCL Wiki.
Categories Section
| Category Numerical Analysis | Category Toys | Category Calculator | Category Mathematics | Category Example | Toys and Games | Category Games | Category Application | Category GUI |