eigenvalues and electronics

The foundation of computer circuits

Page by Theo Verelst

Of course feel free to comment (with initials or some other way to distinguish comments from my writing), this page is supposed to at least raise dust or make people think.

I don't think the tcl/tk community is much prone to the thinking, but in not so forward circles who often seem to think they can understand computers by really miserable and even evil ideas and projections of human functioning, a lot of wrong and dangerous ideas exist and wither that make people pray to a neon God I don't want to take part in.

Computers are great fun, the best computers, and probably almost the most advanced in the world make me play wonderful music and sounds, or do graphics as I did professionally, and even just playing about with some interesting tcl commands can be fun enough, and certainly challenge ones' functional (decomposition) thinking for hours easily, without thinking about abusing children, ruling and exploiting the world and destroying all human existence.

I've already made this point on the bwise applications and examples page by mentioning the so-called

Flip Flop

circuit, which is basically a circuit that is feeding back data to itself in a consistent way, and can therefore remember a bit of information. Because of the nature of the constituents of the circuit, it can be made to remember, be set to one or to zero, all within even the logic of an infinetely fast and 'unspecial' mathematical construct.

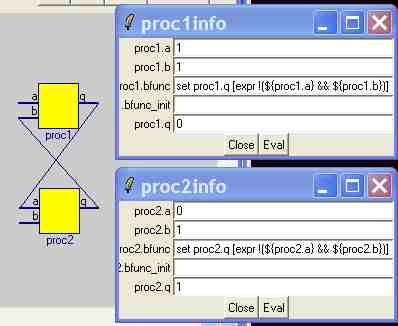
Every electrical engineer should be aware of its existence, though it seems to me that some forget when they enter the world of software engineering.

All messages, data structures, and algorithms are essentially changing the state of such circuits in a computer chip, and in fact almost exclusively that.

Sending a message to an object, or instantiating something from a class, is essentially doing the same: fiddling bits stored by flip flop or similar circuits in a pentium, supersparc, precision architecture, armrisc, cache or dynamic memory chip.

Or changing and regularly updating the magnetisation orientation in a ring memory i nand ancient machine.

And no matter what mind images we'd like to see, or like others to see subdued to, those are the boundaries or the prerequisites of software of any kind, whether it in the end makes a mobile phone beep, a screen turn some colour, or certain dot patterns on paper. There is nothing else that is the carrier or basic material or construct of software, except maybe for using materials that exhibit quantum behaviour or are used to generate noise.

The flip flops contain binary data, which can be used to generate new data, which is a process that can be theorized or designed around by seeing it such that all remembered data in a computer, or in its core to begin with, is taken as the input to the big function that is all of the logic circuits of the computer or CPU chip acting on the current state of all memory elements.

This is possible because we use not singular memory elements, but two flip flops on a row, which is called a 'master-slave' flip flop arrangement (I didn't invent the terminology, it's common among digital electronicists), which are driven by the rising and falling edges of the 'clock' signal that paces all activities in the processor, so that only one change at the time happens.

The jtag connection on a modern pentium (I did an article on the subject at uni long ago) is a clear indicator of such thinking: it puts all memory elements on the chip on a row, allowing an outside machine to shift data into and out of the chip, so all circuits can be tested by applying suitable test patterns to the input which is then shifted into place in the memory elements, to see what all logical functions generate as output, which is clocked into the state maintaining memory after all logic has generated new stable output, and shifted out for analysing.

When chips or parts with different clock pulses are connected together, this approach is harder or impossible, though the thinking remains similar, one then probably works along the long existing lines of telephone or other telecom exchange devices, using protocols and message definitions, which are then carried by machines that are composed of the above kind of machine, called 'Finite State Machines'.

The idea is that all of these designs as soon as possible get away from the logic that is overriding in electronics, where signals are always influencing each other all the time, so that it is not possible to think along lines of simple signal progression without feedback, as is attractive about functional designs.

Using state and functions that act on a state, we decouple the function that computes the new state from the memory circuits, which makes complicated circuits manageable.

In electronics, when we simulate a circuit, that is use a computer program to compute what a certain circuit does, that takes the complicated solving of a system of equations, not a small one, and usually not a linear one to arrive at for instance a representation of the input-output relations or maybe a graph of a frequency response or a signal wave form.

In digital circuits, functions can be represented by truth tables or maybe connected functions, and memory cells store information on command.

In software, not many take into account that in fact the state of a process, to use that common unix term together with the functions in it, with the exception of signals or intetrupts, evolves according to the logic in its function acting on the state at every moment.

In the end it's the logic in the processor chip, most easily represented by the machine language (assemlby) that is in the memory that completely without any bit unaccounted for determines what goes on in the computer. Unless it is in error, which happens quite rarely.

Not that this is earth shattering news, but it seems that in this time software has no intentions along these lines anymore, often. Because machines are man made and there is no reason not to make them do what we want, with complete definitions of that. Which means on the other hand that they don't tell us what life is like, primarily.

Mathematically one could say that the eigenvalue of the nands being fed back to themselves in memory state is one. Electronically, the circuits are nonlinear amplifiers with a delay and a time constant.

Digitally, the memory cell is a latch, possibly a edge-triggered one, when it is master slave.

Everything which goes above this is crap or unknown to me.

Is that all easy? No.

Of course not, the number of memory cells is huge, and the number of possible functions (which in digital kingdoms can be changed dynamically easily) to arrive at the next state is about infinite, except of course we can put only so much on a chip, and so many chips together. The fun part is that a intentional digital design will have the whole domain and range of that function covered and the whole of the relevant part of the function mapping known, but the number of countable possibilities is the number of elements in the domain times the number of elements in the range, which is upper bounded by the number of bits, giving

pow(2,bits_in_domain) * pow(2,bits_in_range)

which is a large number for the number of bits in even a small microcomputer chip.

Not large enough, though. The number of functions from an n-set (set with n elements) to an r-set (set with r elements) is, in your notation, pow(r,n), because for each of the n elements in the domain there is a choice of r possible results, and all these choices are independent. With n = pow(2,bits_in) and r = pow(2,bits_out) this implies that the actual number of functions that can be implemented as a stateless electric curcuit with bits_in input lines and bits_out output lines is

pow( pow(2,bits_out), pow(2,bits_in) )  =  pow(2, bits_out * pow(2,bits_in) )

and that is a lot more than what you stated above. / Lars H

{Interesting point. The reasoning is that one may fill a piece of ROM memory with the transition table, the address lines span the domain of the state, the content of the equal width data bus would be the new state for each of the elements in the domain, which is the range of the map and exhaustively listed by the whole content of the memory. The number of possible state transition tables would be in the order of pow(2,numberofbitsinthememory = width_databus * pow(2,width_addressbus) ) it would seem. Whether these are all relevant and irreducible and useful is another question, such that always one can dicard the possibility of the state machine which loops its initial state. Call a memory an array with discete and known and fixed number of elements and set of possible element values for the sw equivalent. }

Suppose we have 8 bits only, and a function that makes a new state based on those 8 bits, we would have a possible number of distinct mappings, so state progression possibilities of 65536.

With 16 bits of state, which is only the number of bits in the lower part of the A register of a pentium, that number goes up to 4Gig.

Enumerating state progression possibilities for even this simplistic case is almost ridiculous.

Suppose we'd limit ourselves to some function with well behaved mapping based on understandable portions of domain and reach, we could for instance make the divisions in domain and range based on small number or zero, positive negative, infinite, and in between, and define addition based on these possibilities.

The number of actual computations most programmers deal with are relatively limited, and the amount of memory we have at our disposal and use grows maybe even faster then the evolution of computer chips integration levels, adding maybe resource files for foreign languages as interesting addition, but a lot of extra data to debug mainly, probably.

The complexity of electronics is guided by how circuits respond to very concise and measurable and computable quanities and qualities. Even leaving one relevant characteristic out of a electronical circuit definition or part specification can be quite desastrous.

Computer programs are often very poorly defined in terms of demands and any kind of qualitative or quantative measures, probably with the exception of certain types of functions such as OS functions and scientific programs.