gingerbread man
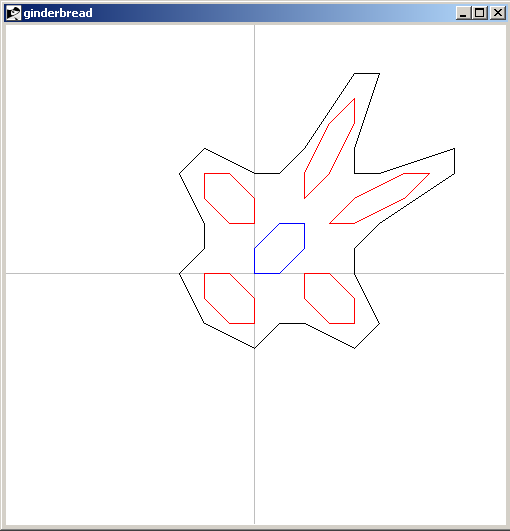
Arjen Markus (22 january 2010) The other day I came across the Gingerbreadman Map [L1 ], a surprisingly simple two-dimensional map that shows regions of chaotic behaviour. That is, if you repeatedly apply the map to adjacent points, they end up in completely different parts of the plane after a number of iterations.
The map is defined in this way:
xnew = 1 - y + |x|
ynew = xSince the map is piece-wise linear, line pieces will remain line pieces (though they might be broken up). To get a better idea of how it works, I wrote the program below. Enjoy!
# gingerbread.tcl --
# Draw the gingerbreadman map - or at least parts of it
#
# mapLine --
# Repeatedly map a line piece using the gingerbreadman map
#
# Arguments:
#
# n Number of mappings
# x1 X-coordinate of first point
# y1 Y-coordinate of first point
# x2 X-coordinate of second point
# y2 Y-coordinate of second point
# colour Colour of the line
#
# Result:
# None
#
# Side effect:
# New line drawn on canvas
#
proc mapLine {n x1 y1 x2 y2 {colour black}} {
.c create line $x1 $y1 $x2 $y2 -fill $colour
for { set i 0 } { $i < $n } { incr i } {
lassign [mapGinger $x1 $y1] x1 y1
foreach [mapGinger $x2 $y2] x2 y2
.c create line $x1 $y1 $x2 $y2 -fill $colour
}
}
# mapGinger --
# Map the coordinates
#
# Arguments:
# x X-coordinate
# y Y-coordinate
#
# Result:
# List of the new coordinates
#
proc mapGinger {x y} {
set xnew [expr {1.0 - $y + abs($x)}]
set ynew $x
return [list $xnew $ynew]
}
# main --
# - Set up the canvas
# - Draw several line pieces
# - Rescale
#
pack [canvas .c -bg white -width 500 -height 500]
.c create line -10.0 0.0 10.0 0.0 -fill grey
.c create line 0.0 -10.0 0.0 10.0 -fill grey
mapLine 30 1.0 -2.0 2.0 -2.0
mapLine 30 3.0 -2.0 4.0 -2.0 red
mapLine 30 0.0 0.0 1.0 0.0 blue
#mapLine 30 0.0 -3.0 1.0 -3.0 red
#mapLine 30 0.0 -3.1 1.0 -3.1 blue
#mapLine 30 0.0 -2.9 1.0 -2.9 green
.c scale all 0 0 25 -25
.c move all 250 250
Here is the result: