mapproj

http://tmml.sourceforge.net/doc/tcllib/mapproj.html

The 'mapproj' package in tcllib contains the conversions between geodetic (See geodesy) and map co-ordinates for a variety of map projections. A large number of projections are supported, because different applications have different needs.

Choosing a Projection

The mapproj manual gives a discussion of the choice of projections. Here is a review that attempts to illustrate some of the major points.

First: What sort of data are you displaying?

• Are directions the key point (winds, ocean currents, magnetic fields, navigational headings?) These are directional data; for directional data, you usually need a conformal projection.
• Are properties of the land or water the key point (temperature, population density, land use, demographics, etc.?) These are thematic data. For thematic data, you usually need an equal area projection.
• Is the significant aspect of your data that it shows distances from (or near to) a specific point? If so, you need an equidistant projection.
• Is the significant aspect of your data that it shows directions from (or near to) a specific point (for instance, radio antenna pointing, air routes, sight lines?) If so, you need an azimuthal projection
• Do you have mixed data, or political data? You'll probably want a projection that is a compromise among the concerns above.

Second: What scale is your map?

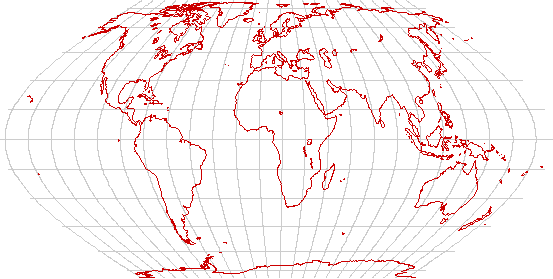
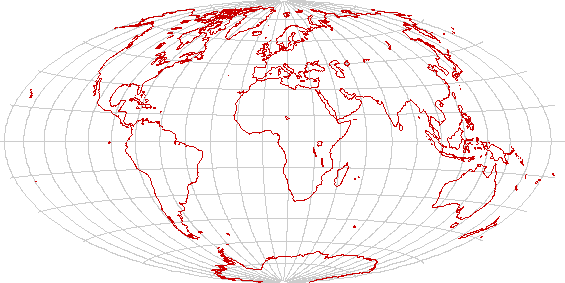
• Is it global? All projections are going to be compromises. The Mercator projection is conformal, but grossly distorts land areas. Several attractive equal-area projections are available. In addition, the Robinson projection gives attractive political world maps, and the Peirce Quincuncial projection, while curious, distorts landforms very little.
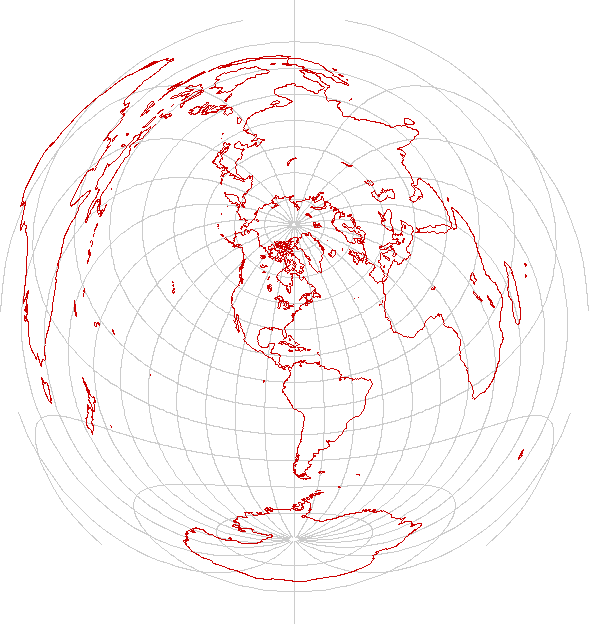
• Is it a map of a hemisphere (or a large fraction thereof?) The stereographic, azimuthal-equidistant, Hammed and Mollweide projections all can project a hemisphere onto a circle.
• Is it a large area (a few hundred km on a side?) The most attractive choice of projection depends on where on the globe it is, and whether it has a predominantly east-west or north-south extent.
• Is it a small area? In order to have map scales correct, you need to lift co-ordinates from the reference ellipsoid onto a sphere. See geodesy for a more detailed discussion.

Examples of Projections

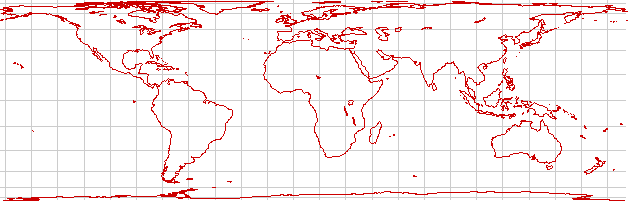
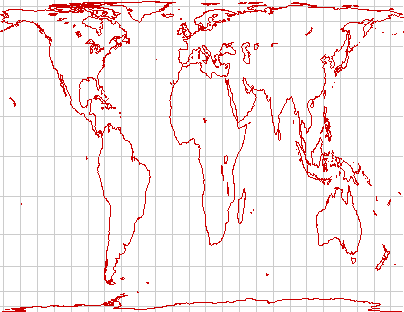
Cylindrical Equal Area

Cylindrical equal-area projections have the advantage that they preserve land areas. Equal-area projections are, of course, preferred to present data on land use, or to present demographics. They do not have the fault of the traditional Mercator projection of exaggerating the visual importance of the high latitudes.

For any cylindrical equal-area projection, there will be one latitude (or rather, a pair of equal latitudes, North and South) where landforms are preserved. Above the standard latitude, landforms will be stretched east to west. Below it, they will be stretched north to south.

Lambert

The Lambert cylindrical equal-area projection is a cylindrical equal-area projection with a standard latitude of the Equator. It preserves equatorial landforms especially well but distorts the temperate and polar regions. It is well suited to thematic maps of countries such as Indonesia that lie near the Equator and extend primarily east and west.

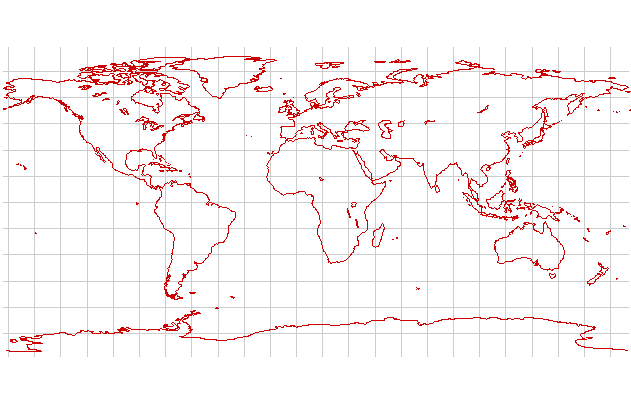
Behrmann

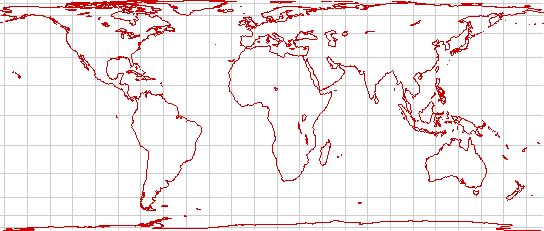
The Behrmann projection is a cylindrical equal-area projection with a standard latitude of ±30°. It is a compromise between equatorial and temperate regions but still gives considerable distortions at high latitudes. It's a reasonable choice for thematic world maps if a rectangular display is desired.

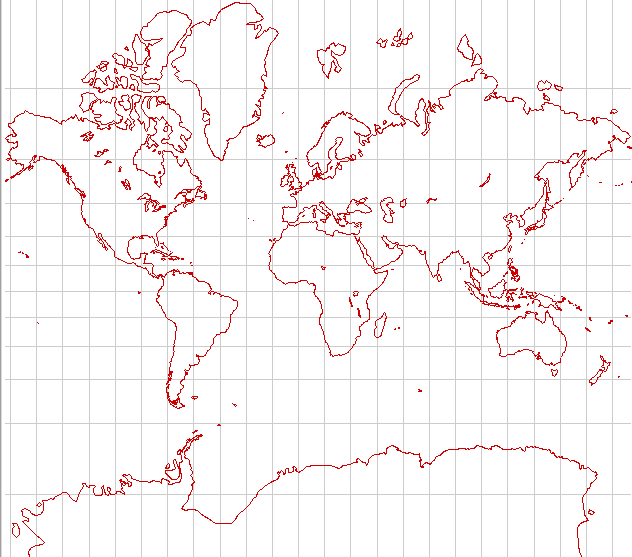
Trystan Edwards and Hobo-Dyer

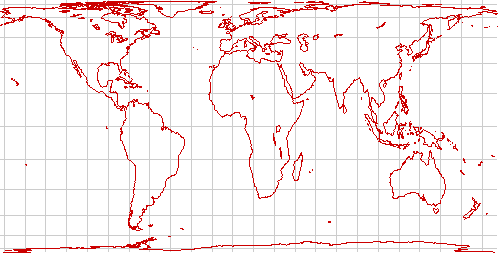
The Trystan Edwards and Hobo-Dyer projections are almost identical. (one has a standard latitude of ±37.4° while the other has ±37.5°) They attempt to give better landforms in the temperate regions without sacrificing too much fidelity in the equatorial regions. It's a good choice for thematic world maps if a rectangular display is desired.

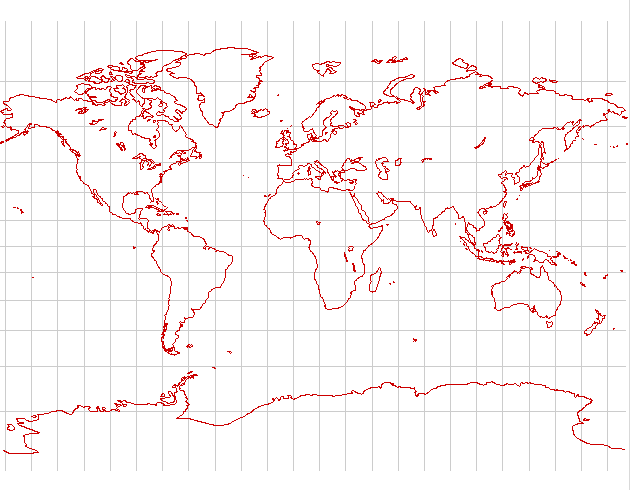
Gall-Peters

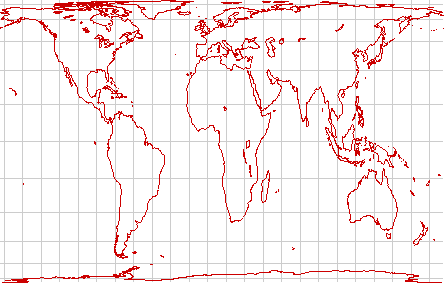
The Gall-Peters projection has a standard latitude of ±45°. It attempts to preserve temperate zone landforms, but stretches the equatorial regions considerably. Thematic maps whose emphasis is primarily the temperate regions show well on this projection.

Balthasart

The Balthasart projection, with its standard latitude of ±50°, is unabashedly Eurocentric. It preserves the landforms of Europe, Canada, Argentina and New Zealand quite well, but distorts much of the rest of the globe.

Cylindrical Equidistant

The cylindrical equidistant projection is also known as the plate carrée In it, all lines of latitude and longitude are vertical and horizontal; its North-South scale is consistent across the entire map. It is chiefly of historical interest because it is one of the easiest projections to construct. It is also still useful for large-area maps of equatorial regions that run primarily east and west. It's a poor choice for world maps because it preserves neither landforms nor areas especially well.

Cylindrical Conformal (Mercator)

In times gone by, the Mercator projection was seen in grade-school classroms throughout the globe. It is a conformal projection; that is, it preserves the local shape of landforms. It also has one property that was indispensible in the days of sail; a straight line on the map represents a constant compass course. (It is not a great circle, unless it is the Equator or a meridian!) Those properties make it useful for some special purposes, but its gross area distortions (showing Greenland as larger than South America, for instance) make it a poor choice as a world map.

Miller Cylindrical

The Miller cylindrical projection is an attempt to preserve the appearance of the traditional Mercator map while mitigating the most extreme distortions in the polar regions. Except for the fact that it gives a traditional look to the map, it's not very useful; it's perhaps best suited to maps that will be treated as works of art.

Pseudo-Cylindrical

A number of projections derived from the cylindrical projection are useful for large-area (and world maps).

Eckert's projections

The Eckert IV and Eckert VI projections are equal-area projections that represent the Poles by straight lines half the length of the Equator. Eckert IV represents meridians by semi-ellipses, while Eckert VI represents them with sinusoids. Both are good compromise projections for use in maps of the world, giving considerable less landform distortion than any of the cylindrical projections while still preserving areas.

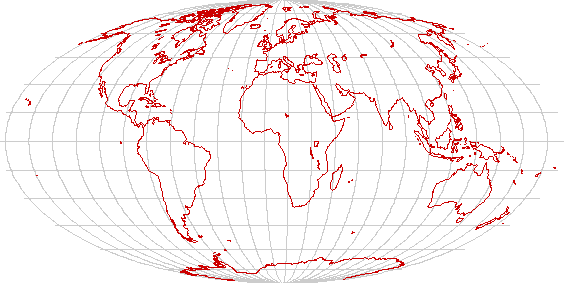
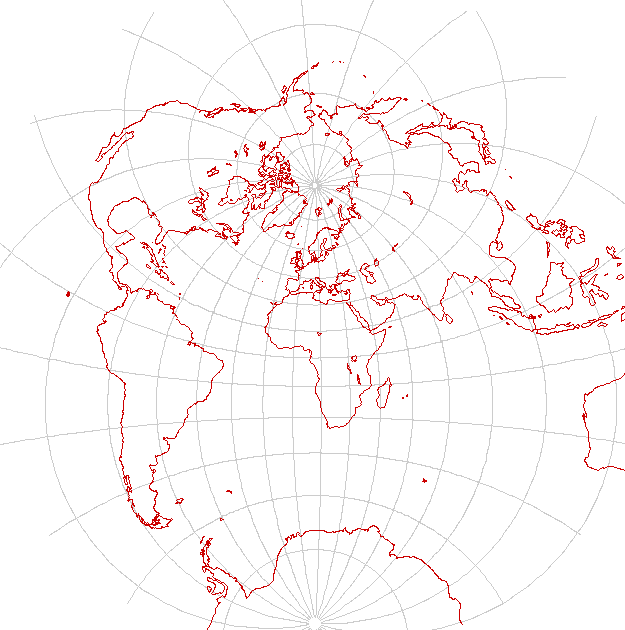
Mollweide's projection

The Mollweide projection is an equal-area projection that represents the poles as points and the meridians as semiellipses. It is an equal area projection (achieved by distorting the scale of latitudes). Its scale is correct only at the center of the map.

It is another useful compromise world map, making a good tradeoff on landforms. It is especially popular in interrupted form, where the projection is interrupted in the oceans in order to show the continents more accurately. Half a Mollweide map can give an attractive circular map of a hemisphere.

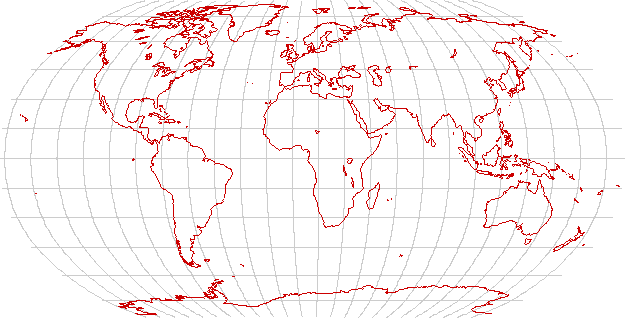
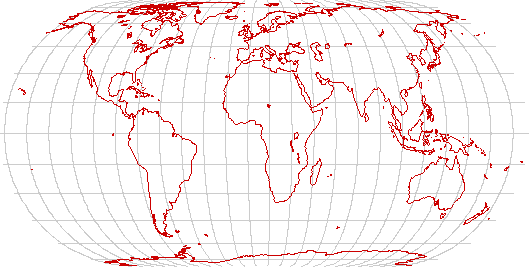
Robinson's projection

The Robinson projection is neither conformal, nor equidistant, nor equal-area. It is defined by interpolation in a table, rather than by mathematical functions. It is designed to be a good compromise for global political maps, since country boundaries anywhere in the world are reasonably clearly represented on it. It is undeniably useful for that purpose.

Sanson-Flamsteed sinusoidal projection

The sinusoidal projection is an equal-area projection where the Poles are represented as points, the meridians as sinusoids, and the parallels as equally spaced straight lines. It is somewhat unattractive as a world map, but (like the Mollweide projection) looks considerably better in interrupted form. It is also effective for thematic presentation of large equatorial regions with a predominantly north-south extent; the Nile valley (or even the whole of Africa) would show well on it. Even Argentina or Norway would not look bad on it, although they would probably show better with the Cassini projection.

Hammer's projection

Hammer's projection offers an even better approximation at landforms than Mollweide's. Like Mollweide's projection, it is also equal-area. It is popular to use Hammer's projection in interrupted form on world maps, although it doesn't show too badly even on continuous maps.

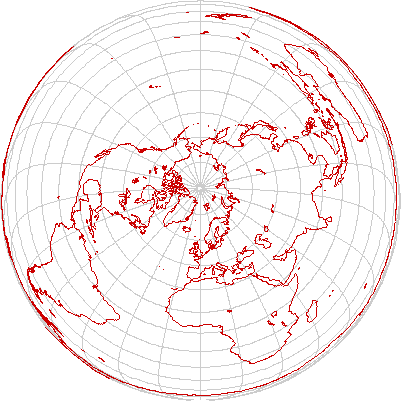
Azimuthal projections

In azimuthal projections, the great circle heading from the center of the map to any other point is preseved. These maps are often the maps of choice for small-area maps. They also are useful for the polar regions (where cylindrical projections are nearly useless) and for special purposes such as antenna pointing and great circle navigation.

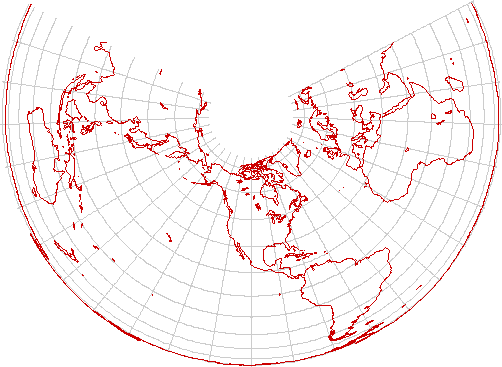
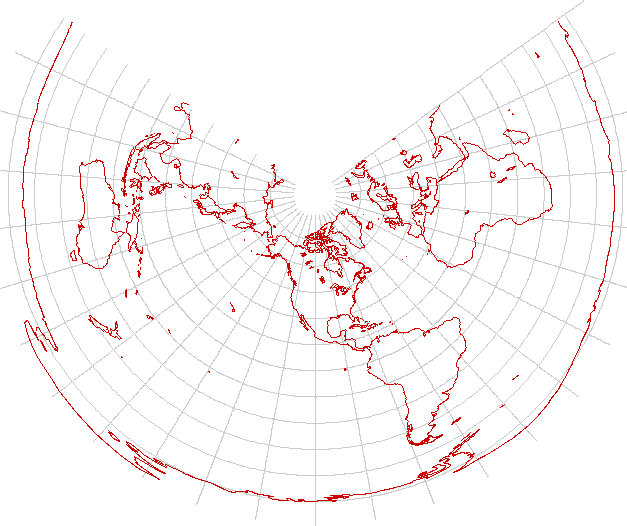
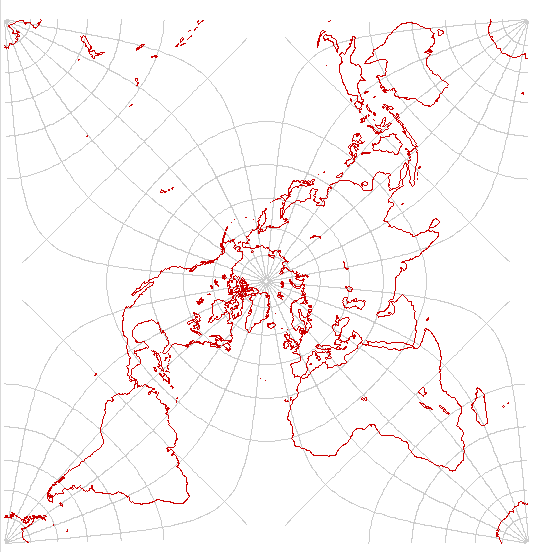
Azimuthal equidistant

The azimuthal equidistant projection preserves distances as well as directions from the center of the map. It is also beloved as a world map by radio operators and planners of air routes; from the center of the map, the great circle bearing and range to any other point in the world can be measured directly. Shown here is such a chart, centered on New York City.

Gnomonic

The gnomonic projection is an azimuthal projection having the unique property that all great circles are represented as straight lines. It therefore allows the shortest path between two points to be plotted with a simple straightedge. The price of this property is that the gnomonic projection can represent only areas much smaller than a hemisphere, and has the worst distortion of landforms and areas of any projection in common use.

Lambert azimuthal equal-area

The Lambert azimuthal equal area projection preserves land areas. It is an excellent choice for thematic maps of the polar regions.

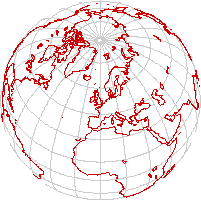
Orthographic

The orthographic projection presents a view of the globe as seen from infinitely far away. It's perhaps of greatest value as a curiosity. But it does make pretty pictures of globes.

Stereographic

The stereographic projection is an azimuthal projection that is also conformal: that is, it preserves the shape of any small region of the world. It shares with all conformal projections the problem that regions near the edge of the map have colossal area distortions.

Conic projections

Conic projections show meridians as straight lines intersecting at one of the Poles. They are popular choices for maps on the scale of continents.

Albers's equal area conic

The Albers projection preserves areas and is therefore a good choice for thematic mapping. It requires the choice of two standard parallels on which map scales will be correct. Between the standard parallels, the latitude scale is too large; outside them, it is too small. A good choice for standard parallels is often 1/6 to 5/6 of the range of latitudes to be displayed. The map above shows an Albers map suitable for displaying North America, with standard parallels at 30° and 60° North.

Conic equidistant

The conic equidistant projection has correct scale along any meridian. Scale is correct on two standard parallels; it is too large outside them and too small between them. The map above shows a conic equidistant map suitable for displaying North America, with standard parallels at 30° and 60° North.

Lambert's conformal conic

The Lambert conformal conic projection, like all conformal projections, preserves the local shape of small areas. Like all conformal projections, it does so at the cost of tremendous area distortions away from the intended region. The map above shows a Lambert conformal conic suitable for displaying North America. The standard parallels are set to 30 and 60 degrees.

Polyconic projections

The mapproj package implements no polyconic projections at present. At least the North American Polyconic should be done, because a great many older US Geologic Survey maps use this projection.

Transverse projections

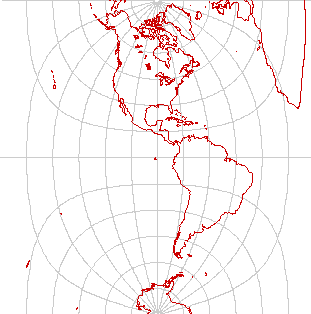
Cassini's projection

The Cassini projection is analogous to the cylindrical equidistant projection, except that it is projected from a standard meridian, instead of from the equator. It is not equal-area or conformal, but it gives excellent representation of any region that has a predominantly north-south extent, and is nearly ideal for maps of countries such as Norway, Argentine and Chile. It is also a popular choice for rectangular maps of the Americas, as shown here.

Universal Transverse Mercator

The Universal Transverse Mercator is another projection that is needed in the library and not yet implemented. It is used by the classic "One in a Million Map" (a map of the entire Earth at 1:1,000,000 scale) and the World Aeronautical Charts.

Curiosities

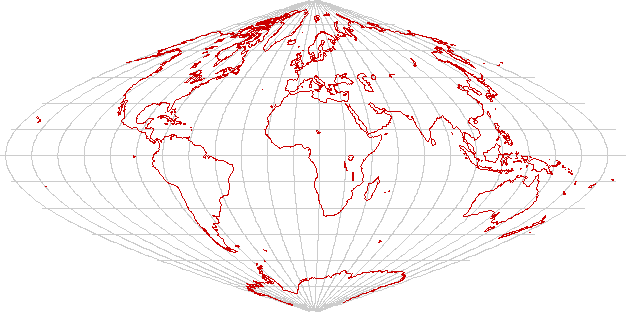
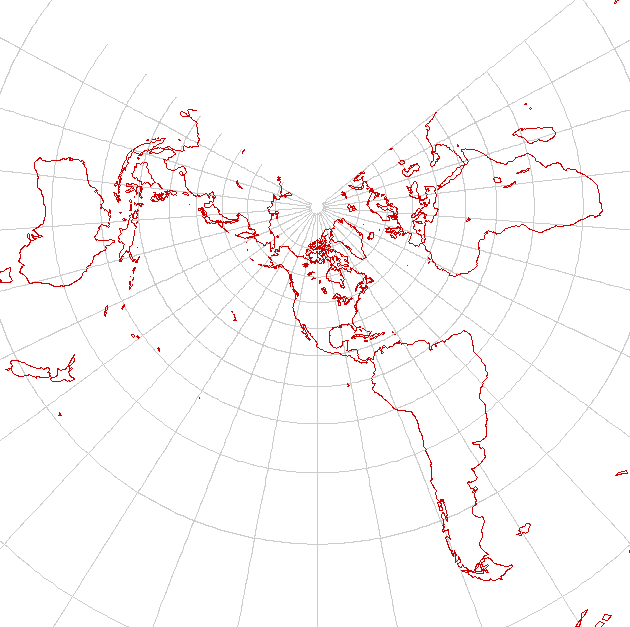
Peirce's quincuncial projection

The Peirce quincuncial projection is an unusual projection of the globe into a square. When parameters are chosen properly, no major land mass is horribly distorted. The projection has the odd feature that it tiles the plane: moving out the side of the Peirce projection moves into an adjacent point on an identical (but inverted) tile. The projection deserves to be better known than it is.

AMG: The Dymaxion projection [L1 ] is pretty cool:

KBK Are you volunteering to add it to tcllib?

AMG: Naah, I haven't done anything with it yet except stare at this animation. :^) I do have a project in mind that would benefit from it, but unfortunately the project is non-Tcl/Tk, and it'll probably be a long time before I get assigned back to that project. If I get a chance to implement it there, I might consider contributing it to tcllib as well. I'd also love to integrate Tcl/Tk. :^)

DKF: The Stereographic Projection has the property of mapping great circles to circles (potentially of infinite size, when the great circle passes through the projection origin).

pd: For universal transverse mercator you could use the proj4tcl library which is a wrapper around the standard proj library. There's an example on the manpage https://github.com/proj4tcl/proj4tcl/blob/main/doc/proj.md

In fact, most of the projections mentioned above are supported by proj. See https://proj.org/operations/projections/index.html