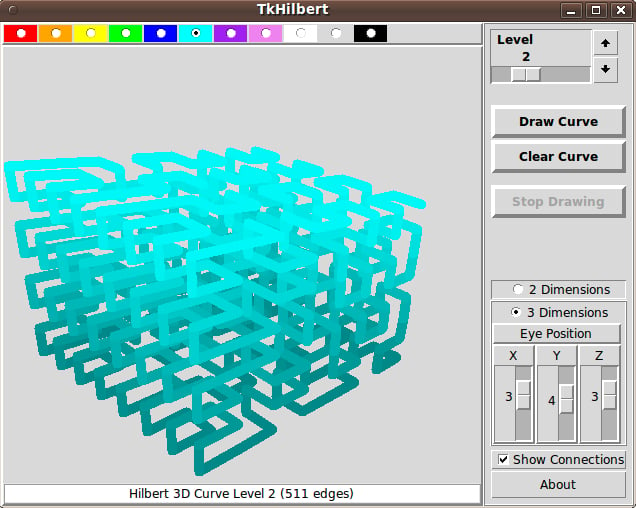
3D Hilbert Curve
Keith Vetter 2003-04-07: this whizzlet draws both the standard Hilbert Curve and a analogous one in 3-dimensions.
One clever aspect of this program is how it does hidden surface removal. The simple painters algorithm--drawing distant objects first so nearer objects paint over obscured surfaces (as used in Fractal Mountains)--doesn't work easily because the components of the curve can't be generated in a back-to-front ordering.
Instead, it uses tk's canvas stacking order. As each object gets generated it is tagged with its depth; then when everything is drawn, then canvas raise is used to place nearer objects before distant ones. This method won't work for complex objects but for the simple ones here it makes an effective hidden surface algorithm.
LV is there a relationship between this code and the sdarchive starkit that talks about the same thing?
In cases where wiki code is turned into starkits, perhaps the starkit's url could be added to the appropriate page, and, vice versa, the wikit page could be placed in the starkit's help information, so that someone with problems knows where to submit questions and comments?
##+########################################################################## # # hilbert3d.tcl -- draws the Hilbert Curve in both 2 and 3 dimensions # by Keith Vetter # package require Tk namespace eval 3D { variable matrix variable 3d set 3d(ex) 3 ;# Eye position set 3d(ey) 4 set 3d(ez) 3 set 3d(rx) 0 ;# Reference point set 3d(ry) 0 set 3d(rz) 0 } array set S {lvl 0 color cyan connect 1 3d 3 eye 3 3Dtype 0} array set DIRS {E {S E E N} N {W N N E} S {E S S W} W {N W W S}} array set QTRS {E {1 2 3 4} N {3 2 1 4} S {1 4 3 2} W {3 4 1 2}} array set XY {E {l t r t r b l b} N {r b r t l t l b} W {r b l b l t r t} S {l t l b r b r t}} array set hpath3d { 0,start 1 0,path {X z x Y X Z x} 0,sub { 1 2 2 20 20 4 4 5} 1,start 1 1,path {z Y Z X z y Z} 1,sub { 6 7 7 19 19 9 9 10} 2,start 1 2,path {X Y x z X y x} 2,sub {11 0 0 23 23 14 14 15} 3,start 4 3,path {x Z X Y x z X} 3,sub {16 17 17 7 7 13 13 8} 4,start 2 4,path {X y x Z X Y x} 4,sub {19 14 14 10 10 0 0 22} 5,start 7 5,path {z y Z x z Y Z} 5,sub {23 9 9 15 15 7 7 21} 6,start 1 6,path {Y X y z Y x y} 6,sub { 0 11 11 13 13 15 15 14} 7,start 1 7,path {z X Z Y z x Z} 7,sub { 2 1 1 3 3 5 5 4} 8,start 2 8,path {Z y z X Z Y z} 8,sub {21 18 18 11 11 20 20 23} 9,start 7 9,path {z x Z y z X Z} 9,sub {13 5 5 14 14 1 1 17} 10,start 4 10,path {Y x y Z Y X y} 10,sub { 3 15 15 4 4 11 11 12} 11,start 1 11,path {Y z y X Y Z y} 11,sub { 7 6 6 8 8 10 10 9} 12,start 7 12,path {x z X y x Z X} 12,sub { 5 13 13 18 18 17 17 1} 13,start 7 13,path {x y X z x Y X} 13,sub {22 12 12 6 6 3 3 19} 14,start 2 14,path {X Z x y X z x} 14,sub { 8 4 4 9 9 2 2 16} 15,start 4 15,path {Y Z y x Y z y} 15,sub {20 10 10 5 5 6 6 18} 16,start 4 16,path {Z Y z x Z y z} 16,sub {10 20 20 22 22 18 18 6} 17,start 4 17,path {x Y X Z x y X} 17,sub {15 3 3 21 21 12 12 11} 18,start 2 18,path {Z X z y Z x z} 18,sub { 4 8 8 12 12 16 16 2} 19,start 2 19,path {y Z Y X y z Y} 19,sub {18 21 21 1 1 23 23 20} 20,start 4 20,path {Z x z Y Z X z} 20,sub {17 16 16 0 0 8 8 13} 21,start 2 21,path {y X Y Z y x Y} 21,sub {14 19 19 17 17 22 22 0} 22,start 7 22,path {y z Y x y Z Y} 22,sub { 9 23 23 16 16 21 21 7} 23,start 7 23,path {y x Y z y X Y} 23,sub {12 22 22 2 2 19 19 3} } proc DoDisplay {} { global S wm title . TkHilbert option add *Scale.highlightThickness 0 option add *Scale.orient horizontal pack [frame .ctrl -relief ridge -bd 2 -padx 5 -pady 5] \ -side right -fill both -ipady 5 pack [frame .top -relief raised -bd 2] -side top -fill x pack [frame .screen -bd 2 -relief raised] -side top -fill both -expand 1 canvas .c -relief raised -borderwidth 0 -height 500 -width 500 label .msg -textvariable S(msg) -bd 2 -bg white -relief ridge pack .msg -side bottom -fill both -in .screen pack .c -side top -expand 1 -fill both -in .screen set colors {red orange yellow green blue cyan purple violet white} lappend colors [lindex [.c config -bg] 3] black foreach color $colors { radiobutton .top.b$color -width 1 -padx 0 -pady 0 -bg $color \ -variable S(color) -value $color -command ReColor bind .top.b$color <3> [list .c config -bg $color] } eval pack [winfo children .top] -side left -fill y DoCtrlFrame ReColor trace add variable S(draw) write Tracer trace add variable S(3d) write Tracer bind .sLevel <ButtonRelease-1> {if {! $S(draw)} DrawHilbertA} } proc DoCtrlFrame {} { frame .ctrl.top scale .sLevel -from 0 -to 7 -label Level -variable S(lvl) -relief ridge .sLevel configure -font "[font actual [.sLevel cget -font]] -weight bold" button .draw -text "Draw Curve" -command DrawHilbertA -bd 4 button .clear -text "Clear Curve" -command {.c delete all} -bd 4 button .stop -text "Stop Drawing" -command {set S(draw) 0} -bd 4 .draw configure -font "[font actual [.draw cget -font]] -weight bold" .clear configure -font [.draw cget -font] .stop configure -font [.draw cget -font] image create bitmap ::img::up -data { #define up_width 11 #define up_height 9 static char up_bits = { 0x00, 0x00, 0x20, 0x00, 0x70, 0x00, 0xf8, 0x00, 0xfc, 0x01, 0xfe, 0x03, 0x70, 0x00, 0x70, 0x00, 0x70, 0x00 }} image create bitmap ::img::down -data { #define down_width 11 #define down_height 9 static char down_bits = { 0x70, 0x00, 0x70, 0x00, 0x70, 0x00, 0xfe, 0x03, 0xfc, 0x01, 0xf8, 0x00,0x70, 0x00, 0x20, 0x00, 0x00, 0x00 }} button .up -image ::img::up -command {UpDown 1} button .down -image ::img::down -command {UpDown -1} checkbutton .connect -text "Show Connections" -variable S(connect) \ -relief raised -command ShowConnectors button .about -text About -command About frame .3df -bd 2 -relief ridge radiobutton .2d -text "2 Dimensions" -variable S(3d) -value 2 \ -command DrawHilbertA -relief ridge radiobutton .3d -text "3 Dimensions" -variable S(3d) -value 3 \ -command DrawHilbertA label .leye -text "Eye Position" -bd 2 -relief raised foreach q {x y z} { frame .feye$q -bd 2 -relief raised label .leye$q -text [string toupper $q] scale .eye$q -from -0 -to 10 -relief ridge -length 75 -orient v \ -variable ::3D::3d(e$q) bind .eye$q <ButtonRelease-1> {if {$S(3d)==3 && !$S(draw)} DrawHilbertA} pack .leye$q .eye$q -in .feye$q -side top -fill x } grid .ctrl.top -in .ctrl -row 0 -sticky news grid .sLevel .up -in .ctrl.top -row 0 -sticky news grid ^ .down -in .ctrl.top -row 1 -sticky news grid .draw -in .ctrl -row 21 -sticky ew grid .clear -in .ctrl -row 22 -sticky ew grid .stop -in .ctrl -row 23 -sticky ew -pady 10 grid .2d -in .ctrl -row 31 -sticky ew grid .3df -in .ctrl -row 32 -sticky ew grid rowconfigure .3df 1 -minsize 10 grid .3d - - -in .3df -row 1 -sticky ew grid .leye - - -in .3df -row 2 -sticky ew grid .feyex .feyey .feyez -in .3df -row 3 grid .connect -in .ctrl -row 101 -sticky ew grid .about -in .ctrl -row 102 -sticky ew grid rowconfigure .ctrl 10 -minsize 10 grid rowconfigure .ctrl 20 -minsize 10 grid rowconfigure .ctrl 30 -minsize 50 grid rowconfigure .ctrl 50 -weight 1 grid configure .up -ipadx 5 grid configure .down -ipadx 5 } ##+########################################################################## # # Tracer -- traces the S(draw) variable and activates widgets accordingly # proc Tracer {var1 var2 op} { global S set eyes {.leye .eyex .eyey .eyez .leyex .leyey .leyez} set ww {.up .down .connect .draw .clear .3d} if {$var1 == "S" && $var2 == "3d"} { if {$S(3d) == 3} {set state1 normal} else { set state1 disabled } foreach w $eyes {$w config -state $state1} return } if {$S(draw) == 0} { ;# Turning off drawing .stop config -state disabled .sLevel config -state normal -fg [lindex [.sLevel config -fg] 3] foreach w $ww { $w config -state normal} if {$S(3d) == 3} {foreach w $eyes {$w config -state normal}} } else { .stop config -state normal .sLevel config -state disabled -fg [.up cget -disabledforeground] foreach w $ww { $w config -state disabled} if {$S(3d) == 3} {foreach w $eyes {$w config -state disabled}} } } ##+########################################################################## # # DrawHilbert -- sets up the state and draws the Hilbert curve # proc DrawHilbertA {} {after 1 DrawHilbert} proc DrawHilbert {{lvl {}}} { global S 3D depths if {$lvl == {}} { set lvl $S(lvl) } else { set S(lvl) $lvl } .c delete all set S(draw) 1 set S(first) {} set S(ccolor) [expr {$S(connect) ? $S(color) : [.c cget -bg]}] if {$S(3d) == 3} { set S(width) [expr {$lvl < 3 ? (20 - 5*$lvl) : 5}] set n [expr {int(pow(2,3*($lvl+1)) - 1)}] set S(msg) "Hilbert 3D Curve Level $lvl ($n edges)" catch {unset depths} Hilbert3d $S(3Dtype) $lvl [GetStartCube] ZBuffer } else { set S(width) [expr {$lvl <= 4 ? (25 - 5*$lvl) : 8 - $lvl}] set n [expr {int(pow(4,$lvl+1) - 1)}] set S(msg) "Hilbert Curve Level $lvl ($n edges)" Hilbert [GetStartBox] E $lvl } set S(draw) 0 set S(first) {} if {! $::S(connect)} {.c lower connect} } ##+########################################################################## # # UpDown -- draws the curve one level up or down from current # proc UpDown {dlvl} { global S if {$dlvl < 0 && $S(lvl) == 0} return if {$dlvl > 0 && $S(lvl) >= [.sLevel cget -to]} return incr S(lvl) $dlvl DrawHilbert } ##+########################################################################## # # Hilbert -- draws a specified level Hilbert curve # proc Hilbert {box dir lvl} { global S DIRS QTRS if {! $S(draw)} return if {$lvl == 0} { Hilbert0 $box $dir return } set lvl2 [expr {$lvl - 1}] foreach quarter $QTRS($dir) newDir $DIRS($dir) { set b2 [QuarterBox $box $quarter] Hilbert $b2 $newDir $lvl2 } } ##+########################################################################## # # Hilbert0 -- draws the most basic hilbert curve inside $box facing $dir # proc Hilbert0 {box dir} { global S XY set xy $S(first) ;# Possibly connect to last set xy {} foreach {l t r b} [ShrinkBox $box] break foreach i $XY($dir) { ;# Walk coord list for this dir lappend xy [set $i] } if {$S(first) != ""} { .c create line [concat $S(first) [lrange $xy 0 1]] -width $S(width) \ -tag {hilbert connect} -fill $S(ccolor) } .c create line $xy -tag hilbert -width $S(width) -fill $S(color) \ -capstyle round set S(first) [lrange $xy end-1 end] ;# So next connects w/ this one } ##+########################################################################## # # GetStartBox -- returns coordinates of the area to draw our shape in # proc GetStartBox {} { return [list 9 9 [expr {[winfo width .c]-9}] [expr {[winfo height .c]-9}]] } ##+########################################################################## # # ShrinkBox -- shrinks a box to 1/4 of its size # proc ShrinkBox {box} { foreach {l t r b} $box break set dx [expr {($r - $l) / 4.0}] set dy [expr {($b - $t) / 4.0}] set l [expr {$l + $dx}] ; set r [expr {$r - $dx}] set t [expr {$t + $dy}] ; set b [expr {$b - $dy}] return [list $l $t $r $b] } ##+########################################################################## # # QuarterBox -- Returns coordinates of 1 of the 4 quadrants of BOX. # 1 = up/left, 2 = up/right, 3 = lower/right, 4 = lower/left # proc QuarterBox {box corner} { foreach {l t r b} $box break set hx [expr {($r - $l) / 2.0}] set hy [expr {($b - $t) / 2.0}] if {$corner == 1} { ;# Upper left set r [expr {$r - $hx}] set b [expr {$b - $hy}] } elseif {$corner == 2} { ;# Upper right set l [expr {$l + $hx}] set b [expr {$b - $hy}] } elseif {$corner == 3} { ;# Lower right set l [expr {$l + $hx}] set t [expr {$t + $hy}] } elseif {$corner == 4} { ;# Lower left set r [expr {$r - $hx}] set t [expr {$t + $hy}] } return [list $l $t $r $b] } proc ShowConnectors {} { if {$::S(connect)} { .c itemconfig connect -fill $::S(color) ZBuffer } else { .c itemconfig connect -fill [.c cget -bg] .c lower connect } } proc ReColor {} { global S foreach {S(red) S(green) S(blue)} [winfo rgb . $S(color)] break if {$S(color) == "black"} { foreach {S(red) S(green) S(blue)} [winfo rgb . white] break } if {$S(3d) == 3} { if {[.c find withtag line] != {}} { after 1 DrawHilbert } return } .c itemconfig hilbert -fill $::S(color) if {! $::S(connect)} {.c itemconfig connect -fill [.c cget -bg]} } proc About {} { set msg "TkHilbert\nby Keith Vetter, Feb 2003\n\n" append msg "Draws the Hilbert Curve and a 3-Dimensional analog.\n" append msg "This curve was discovered by David Hilbert in 1891 and\n" append msg "was one of the first plane-filling curves ever found." tk_messageBox -title "About TkHilbert" -message $msg } ##+########################################################################## # # 3D Hilbert curver routines # proc GetStartCube {} { global 3D set 3D(X) [expr {[winfo width .c] - 20}] set 3D(Y) [expr {[winfo height .c] - 20}] set 3D(X2) [expr {$3D(X) / 2.0}] ;# Mid-point set 3D(Y2) [expr {$3D(Y) / 2.0}] set 3D(X3) [expr {$3D(X2) - 100.0}] ;# Scaling factor set 3D(Y3) [expr {$3D(Y2) - 120.0}] 3D::Init return [list 1 1 1 -1 -1 -1] } ##+########################################################################## # # Hilbert3d # # Main routine to draw a 3-D Hilbert curve. If level is 0 then we just # draw the base figure (with TYPE orientation). Otherwise we divide up # the volume (CUBE) into 8 quadrants in the order of the path for TYPE. # We then draw Hilbert curves in each of the quadrants of LEVEL - 1. # proc Hilbert3d {type lvl c} { global S hpath3d if {! $S(draw)} return if {$lvl == 0} { Hilbert3d0 $type $c return } # Draw the 8 sub Hilbert shapes for this type. We start in the starting # quadrant for this type, draw the correctly oriented sub-unit based on # the info in hpath3d. We continue along the path for this type and draw # the remaining sub-units. set lvl2 [expr {$lvl - 1}] ;# Down a level set oct $hpath3d($type,start) ;# Octant to start in foreach path $hpath3d($type,path) sub $hpath3d($type,sub) { set c2 [Octant $c $oct] ;# Divide up the cube world Hilbert3d $sub $lvl2 $c2 ;# Draw next level Hilbert curve set oct [NewOctant $oct $path] ;# Move to next octant } } ##+########################################################################## # # Hilbert3d0 -- draws the lowest level of the 3-d Hilbert curve # # hpath3d specifies start corner of the cube and also the path of the curve. # Each letter in the path specifies an axis to follow with capital meaning # to go in. # proc Hilbert3d0 {type c} { global hpath3d foreach {x1 y1 z1 x2 y2 z2} [ShrinkCube $c] break # Get starting location set x [expr {$hpath3d($type,start) & 4 ? $x1 : $x2}] set y [expr {$hpath3d($type,start) & 2 ? $y1 : $y2}] set z [expr {$hpath3d($type,start) & 1 ? $z1 : $z2}] x_line $x $y $z connect ;# Start the line foreach p $hpath3d($type,path) { switch $p { X { set x $x1 } x { set x $x2 } Y { set y $y1 } y { set y $y2 } Z { set z $z1 } z { set z $z2 } } x_line $x $y $z } } proc ShrinkCube {cube} { foreach {x1 y1 z1 x2 y2 z2} $cube break set dx [expr {($x1 - $x2) / 4.0}] set dy [expr {($y1 - $y2) / 4.0}] set dz [expr {($z1 - $z2) / 4.0}] set x1 [expr {$x1 - $dx}] set x2 [expr {$x2 + $dx}] set y1 [expr {$y1 - $dy}] set y2 [expr {$y2 + $dy}] set z1 [expr {$z1 - $dz}] set z2 [expr {$z2 + $dz}] return [list $x1 $y1 $z1 $x2 $y2 $z2] } proc x_line {x y z {connect ""}} { global S foreach {sx sy} [3D::Obj2screen $x $y $z] break lappend S(xyz) $x $y $z if {$S(first) != {}} { foreach {color tag} [DepthColor $S(lastZ) $z] break if {! $S(connect) && $connect != ""} {set color $S(ccolor)} .c create line [concat $S(first) $sx $sy] -fill $color \ -width $S(width) -capstyle round -tag "line $tag $connect" } set S(first) [list $sx $sy] set S(lastZ) $z } ##+########################################################################## # # Obj2screen - converts 3-d coordinates (x,y,z) into screen coordinates. # The eye is fixed on the Z axis and we project onto a x-y plane # through the origin. It boils down to essentially dividing by Z. # proc obj2screen {x y z} { global S 3D set eye $S(eye) set x [expr {double($x) * $eye / ($eye - $z)}] ;# Depth adjustment set y [expr {double($y) * $eye / ($eye - $z)}] set sx [expr {$3D(X2) + round($x * $3D(X3))}] ;# To world coord set sy [expr {$3D(Y2) + round($y * $3D(Y3))}] return [list $sx $sy] } ##+########################################################################## # # DepthColor -- provides depth cueing by shading per depth # proc DepthColor {z1 z2} { global S depths set z [expr {($z1 + $z2) / 2.0}] ;# Mid point depth set z [expr {1 - (($z + 1) / 2)}] ;# Convert to 1-0 scale set zz [expr {1 - $z/2}] ;# .5 - 1 scale set red [expr {int($zz * $S(red))}] set green [expr {int($zz * $S(green))}] set blue [expr {int($zz * $S(blue))}] set color [format "\#%04X%04X%04X" $red $green $blue] set tag [format "Z%03d" [expr {int(999*$z)}]] set depths($tag) 1 ;# Used for Z buffering return [list $color $tag] } ##+########################################################################## # # Octant -- returns a CUBE which is one of the eight sub-quadrants of C # proc Octant {cube which} { foreach {x1 y1 z1 x2 y2 z2} $cube break set hx [expr {($x1 + $x2) / 2.0}] set hy [expr {($y1 + $y2) / 2.0}] set hz [expr {($z1 + $z2) / 2.0}] if {$which & 1} {set z2 $hz} else {set z1 $hz} if {$which & 2} {set y2 $hy} else {set y1 $hy} if {$which & 4} {set x2 $hx} else {set x1 $hx} return [list $x1 $y1 $z1 $x2 $y2 $z2] } proc NewOctant {which dir} { switch $dir { X { incr which 4} x { incr which -4} Y { incr which 2} y { incr which -2} Z { incr which 1} z { incr which -1} } return $which } ##+########################################################################## # # ZBuffer -- do a Z buffer hidden line algorithm by ordering every line # in the canvas stacking list based on the lines "Z###" tag that we # added to every line, the number in which is the depth of the line. # The hash depths keeps a list of all "Z###" tags used. # proc ZBuffer {} { foreach d [lsort [array names ::depths]] { .c lower $d } } ################################################################ ################################################################ ################################################################ ################################################################ ##+########################################################################## # # 3d Canvas # # Simple 3d canvas package. After specifying the eye, the page size and a # few other variables, this package will draw points and lines in 3d space. # # A simple example is given at the bottom. # # This is very simple. No clipping, z-buffering, or rotation is provided. # # Procedures: # 3D::Init # Generates the transformation matrix needed to map from world to screen. # Must be called after setting or changing the eye, etc. # 3D::Line canvas x1 y1 z1 x2 y2 z3 ?x3 y3 z3 ...? ?options? # Draws a line between all the 3d points specified. # # Variables: # 3d(ex) 3d(ey) 3d(ez) == eye position # 3d(rx) 3d(ry) 3d(rz) == reference point # 3d(x) 3d(y) == canvas size # 3d(cx) 3d(cy) == viewport center (reference point goes here) # 3d(sx) 3d(sy) == size of viewport # # Revision history # Keith Vetter 12/17/95 Initial revision from a C based version into tcl. # Keith Vetter 1/10/95 Finished the revision. # ##+########################################################################## # # 3D::Init # # Computes the transformation matrix for the current eye and center. # Note, calling this resets all scaling, translations, etc. # proc 3D::Init {} { variable matrix variable 3d set xy [expr {sqrt($3d(ex)*$3d(ex) + $3d(ey)*$3d(ey))}] set xyz [expr {sqrt($xy*$xy + $3d(ez)*$3d(ez))}] 3D::Ident matrix 3D::Ident t ;# T0 - Center to origin set t(3,0) [expr {-$3d(rx)}] set t(3,1) [expr {-$3d(ry)}] set t(3,2) [expr {-$3d(rz)}] 3D::M44 matrix t matrix 3D::Ident t ;# T1 -- Origin To eye set t(3,0) [expr {-$3d(ex)}] set t(3,1) [expr {-$3d(ey)}] set t(3,2) [expr {-$3d(ez)}] 3D::M44 matrix t matrix 3D::Ident t ;# T2 -- Rotate 90 around X set t(1,1) 0 set t(2,2) 0 set t(1,2) -1 set t(2,1) 1 3D::M44 matrix t matrix if {$xy != 0} { 3D::Ident t ;# T3 -- Rotate to eye line set t(0,0) [set t(2,2) [expr {-$3d(ey) / $xy}]] set t(0,2) [expr {$3d(ex) / $xy}] set t(2,0) [expr {-$t(0,2)}] 3D::M44 matrix t matrix } 3D::Ident t ;# T4 -- Rotate to eye line set t(1,1) [set t(2,2) [expr {$xy / $xyz}]] set t(1,2) [expr {$3d(ez) / $xyz}] set t(2,1) [expr {-$t(1,2)}] 3D::M44 matrix t matrix 3D::Ident t ;# T5 -- Left-Handed coords set t(2,2) -1 3D::M44 matrix t matrix 3D::Ident t ;# N - Scale By D/S set t(0,0) [set t(1,1) 4] 3D::M44 matrix t matrix set 3d(x) [winfo width .c] ;# Page size set 3d(y) [winfo height .c] set 3d(cx) [expr {$3d(x) / 2.0}] ;# Mid-point set 3d(cy) [expr {$3d(y) / 2.0}] set 3d(sx) [expr {$3d(cx) - 5.0}] ;# Viewport size set 3d(sy) [expr {$3d(cy) - 6.0}] } ##+########################################################################## # # 3D::Ident matrix # # Returns $mm as the identity matrix of size 4 # proc 3D::Ident mm { upvar 1 $mm m catch "uplevel [list unset $mm]" ;# Erase all entries foreach a {0,1 0,2 0,3 1,0 1,2 1,3 2,0 2,1 2,3 3,0 3,1 3,2} { set m($a) 0 } set m(0,0) [set m(1,1) [set m(2,2) [set m(3,3) 1.0]]] } ##+########################################################################## # # 3D::M44 ma mb mc # # Matrix multiply ma x mb => mc of size 4. mc can be either ma or mb. # proc 3D::M44 {ma mb mc} { upvar 1 $ma aa upvar 1 $mb bb upvar 1 $mc cc for {set r 0} {$r < 4} {incr r} { set result($r,0) [expr {.0 + $aa($r,0)*$bb(0,0) + $aa($r,1)*$bb(1,0) \ + $aa($r,2)*$bb(2,0) + $aa($r,3)*$bb(3,0)}] set result($r,1) [expr {.0 + $aa($r,0)*$bb(0,1) + $aa($r,1)*$bb(1,1) \ + $aa($r,2)*$bb(2,1) + $aa($r,3)*$bb(3,1)}] set result($r,2) [expr {.0 + $aa($r,0)*$bb(0,2) + $aa($r,1)*$bb(1,2) \ + $aa($r,2)*$bb(2,2) + $aa($r,3)*$bb(3,2)}] set result($r,3) [expr {.0 + $aa($r,0)*$bb(0,3) + $aa($r,1)*$bb(1,3) \ + $aa($r,2)*$bb(2,3) + $aa($r,3)*$bb(3,3)}] } catch "uplevel [list unset $mc]" foreach arr [array names result] { set cc($arr) $result($arr) } } ##+########################################################################## # # 3D::PrintMatrix matrix # # Prints out the 4x4 matrix $mm # proc m {} {::3D::PrintMatrix ::matrix} proc 3D::PrintMatrix {mm} { upvar 1 $mm m for {set r 0} {$r < 4} {incr r} { for {set c 0} {$c < 4} {incr c} { puts -nonewline [format "%.3f\t" $m($r,$c)] } puts "" } puts "" } ##+########################################################################## # # 3D::Obj2screen # # Converts a 3d position into 2d screen coordinates based on the current # transformation matrix matrix set up by 3D::Init. # proc 3D::Obj2screen {x y z} { variable matrix variable 3d set xe [expr {$x*$matrix(0,0)+$y*$matrix(1,0)+$z*$matrix(2,0)+$matrix(3,0)}] set ye [expr {$x*$matrix(0,1)+$y*$matrix(1,1)+$z*$matrix(2,1)+$matrix(3,1)}] set ze [expr {$x*$matrix(0,1)+$y*$matrix(1,2)+$z*$matrix(2,2)+$matrix(3,2)}] set sx [expr $3d(cx) + ($xe / $ze) * $3d(sx)] set sy [expr $3d(cx) - ($ye / $ze) * $3d(sy)] return [list $sx $sy] } ################################################################ ################################################################ DoDisplay bind . <Map> DrawHilbert
uniquename 2013jul29
This code could use an image to show what it produces:
(Thanks to 'gnome-screenshot', 'mtpaint', and ImageMagick 'convert' on Linux for, respectively, capturing the image to a PNG file, cropping the image, and converting the resulting PNG file to a JPEG file about 3 times smaller. Thank you FOSS developers everywhere, from someone who is also contributing FOSS code to the world --- in the form of Tk scripts.)