Babylonian Combined Work Norm Algorithm and eTCL Slot Calculator Demo Example, numerical analysis
Babylonian Combined Work Norms Algorithm and eTCL Slot Calculator Demo Example, numerical analysis
This page is under development. Comments are welcome, but please load any comments in the comments section at the bottom of the page. Please include your wiki MONIKER and date in your comment with the same courtesy that I will give you. Aside from your courtesy, your wiki MONIKER and date as a signature and minimal good faith of any internet post are the rules of this TCL-WIKI. Its very hard to reply reasonably without some background of the correspondent on his WIKI bio page. Thanks, gold 12Dec2018
- Babylonian Combined Work Norms Algorithm and eTCL Slot Calculator Demo Example, numerical analysis
- Introduction
- Pseudocode Section
- Appendix Code
- Console program for harmonic_mean
- Snippet Pseudocode formula
- Hidden Comments Section
Introduction
gold Here is some eTCL starter code for Babylonian combined work norms in calculator shell. Additional console programs below are used to check or improve subroutines in calculator shell.
There are a number of Babylonian problems on combined work norms. The Babylonian method or formula was combined work norm equals 1/(1/norm1 +1/norm2 +1/norm3). Alternately, some Babylonian texts use the method for Babylonian combined work norm as 3/(1/norm1 +1/norm2 +1/norm3), where the change is adjusted in the accounting. The modern term for a similar method is the harmonic mean. However the modern formula is defined as n/(1/norm1 +1/norm2 +1/norm3 ... 1/nth term) for n terms. For the modern reader, some of the difficulty was that some work norms familiar to the Babylonians have to be constructed from the known corpus of Old Babylonian coefficients. In the Babylonian problems, two to five of the work norms were combined. For the eTCL calculator, there were 3 work norms to be combined. The combined work norm units for the eTCL calculator are normally units per man*workdays. The units for the inverse work norms in the eTCL calculator are normally man*workdays per unit.
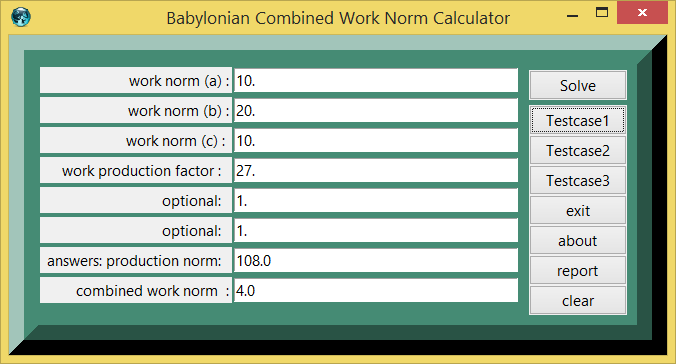
As an example, suppose that Babylonians defined different work norms for making volumes of bricks. The work norm was 10/60 volume units for brick type $aaa, 20/60 volume units for brick type $bbb, and 10/60 volume units for brick type $ccc. Here the volume unit was one sar, equivalent to 18 cubic meters of earth or equivalent to volume of bricks (with the right scale factor or production factor). The Babylonian work norm formula is 1/((1/$aaa)+(1/$bbb)+(1/$ccc)), substituting expr 1./((1./(10./60. ))+(1./(20./60. ))+(1./(10./60.)))=decimal 0.0666 or ~ 4/60 in base60. The eTCL calculator returns a combined work norm of 3.999/60 volume units. The number of bricks is 3.999*27 or 108.0 bricks.
For example, the difficulty in excavating a canal increases with the depth and the Babylonians defined different work norms at each depth level. The work norm was 20/60 volume units between 1 and 2 cubits, 10/60 volume units between 2 and 3 cubits depth, and 8.5/60 volume units between 3 and 5 cubits. Here the volume unit was one sar, equivalent to 18 cubic meters of earth. Suppose a worker spent equal amounts of the work day at each of the three levels. Then his work norm should be the combined work norm of 20/60,10/60 , and 8.5/60. The eTCL calculator returns a combined work norm of 3.73/60 volume units. In modern terms, the production or excavation volume was (3.73/60)*18 cubic meters, 1.1 cubic meters of earth. This answer is reasonably close, but it appears that some offset scheme or partial fractions are being used also. Ref. canal depths in Sumerian Construction Rates on this wiki.
The work norms for the three levels of canal excavation are 20/60,10/60, and 6/60+40/3600 in volume sars. Suppose a canal worker was assigned with the combined work norm of the three levels. The combined work norm was 1/(1/norm1 +1/norm2 +1/norm3), substituting expr(1./(1./(20./60.) +1/(10./60.)+1./(6./60.+40./3600.))) or decimal 0.0555 sars. The combined work norm was equivalent to expr (.0555*18) or 1 cubic meter of earth. The partials of levels 1,2,3 were decimal fractions 0.055555/(20./60.), 0.055555/(10./60.), 0.055555/(6./60.+40./3600.) or 0.1666,0.333,0.4999 day. As a check, the sum of the partials as expr (0.055555/(20./60.) + 0.055555/(10./60.) + 0.055555/(6./60.+40./3600.)) = 0.999, ~1. For this example, production for three days was 3*0.0555 sars or expr(3./(1./(20./60.) +1/(10./60.)+1./(6./60.+40./3600.))) , decimal 0.1665 sars. For the eTCL calculator, the third work norm expr (6./60.+40./3600.)*60. is equivalent to decimal 6.666. Loading the eTCL calculator as 20/10/6.666 returns 3.333 for the base60 fractions and 3.333/60 is the decimal 0.0555 factor from above.
An Ancient Egyptian problem for making sandals was discussed in Unexpected Links between Egyptian and Babylonian Mathematics, Friberg. From the Egyptian problem, the Egyptian work norm for cutting sandals was 10 sandals per man*workday as 10/1. The Egyptian work norm for finishing sandals was 10 sandals per 2 man*workday as 10/2 or reduced as 5/1. The Babylonian method for the combined work norm can be hand calculated as expr (1./ ( 1./( 10./1. ) +1./(10./2. ) ) ), 3.333 pairs of sandals per man*workdays. The eTCL calculator can be loaded as 10/1 and 10/2 (reduced to 5) for the first two work norms. For very large N, the third term reduces to zero and the eTCL calculator returns 3.333 pairs. As a check on the Babylonian method, the Egyptian method or reasoning works well for the overall work norm as expr (10 pairs / 3 days) or 3.333 pairs. Ref Friberg for an exact translation of problem.
Continuing with an Ancient Egyptian problem for making sandals, useful relationships with partial fractions and work times can be developed (which are not mentioned in the ancient text). From the partial work norms and the combined work norm, the partial fraction of a day spent on a task is (combined work norm)/(partial work norm). The sum of all partial tasks as (c. norm)/(norm1)+(c. norm)/(norm2)+(c. norm)/(norm3) ... should equal unity (1 day). For the Egyptian sandals problem, the sum of partial tasks was (c. norm)/(norm1)+(c. norm)/(norm2), substituting expr (3.33/10. + 3.333/5.) = 0.9996, ~1 day. For the problem averages, the sandal maker spent 3.33/10 or 0.333 day on cutting sandals and 3.333/5 or 0.666 day on finishing sandals. Reformulating the partial tasks, (c. norm)/(norm1)+(c. norm)/(norm2) = 1, (c. norm)/(norm1) = 1 - (c. norm)/(norm2). The time spent on norm1 cutting should equal 1 - (c. norm)/(norm2 finishing), substituting expr (1-3.333/5.), 0.333 day. For 3 days, the sandal production was expr (3./ ( 1./( 10./1. ) +1./(10./2. ) ) )), 9.999, ~ 10 pairs of sandals. Similar methods as $n/harmonic_mean in modern expressions have been observed in the Babylonian texts, apparently the production of $n days or the progress of canal excavation combining all levels of depth for $n days.
Pseudocode Section
# using pseudocode
# possible problem instances,
initialize algorithm_result = 1.
check algorithm
f(solution) =? initial product
B. combined work norm equals 1/(1/norm1 +1/norm2 +1/norm3)
B. alternate combined work norm equals 1/(1/norm1 +1/norm2 +1/norm3)
modern formula for harmonic mean equals
n/(1/norm1 +1/norm2 +1/norm3 ... 1/nth term) for n terms
check_sum = a+b+c+d+e
set answers and printout with resulting values
pseudocode: need test cases > small,medium, giant
pseudocode: need testcases within range of expected operation.
pseudocode: are there any cases too small or large to be solved?Testcases Section
In planning any software, it is advisable to gather a number of testcases to check the results of the program. The math for the testcases can be checked by pasting statements in the TCL console. Aside from the TCL calculator display, when one presses the report button on the calculator, one will have console show access to the capacity functions (subroutines).
Testcase 1
| table 1 | printed in | tcl wiki format |
|---|---|---|
| quantity | value | comment, if any |
| 1: | testcase_number | |
| 10.0 : | work norm (a) | |
| 20.0 : | work norm (b) | |
| 10.0 : | work norm (c) | |
| 27.0 : | work production factor : | |
| 1.0 : | optional: | |
| 1.0 : | optional: | |
| 108.0 : | answers: production norm: | |
| 4.0 : | combined work norm |
Testcase 2
| table 2 | printed in | tcl wiki format |
|---|---|---|
| quantity | value | comment, if any |
| 2: | testcase_number | |
| 10.0 : | work norm (a) | |
| 10.0 : | work norm (b) | |
| 20.0 : | work norm (c) | |
| 27.0 : | work production factor : | |
| 1.0 : | optional: | |
| 1.0 : | optional: | |
| 108.0 : | answers: production norm: | |
| 4.0 : | combined work norm |
Testcase 3
| table 3 | printed in | tcl wiki format |
|---|---|---|
| quantity | value | comment, if any |
| 3: | testcase_number | |
| 20.0 : | work norm (a) | |
| 10.0 : | work norm (b) | |
| 10.0 : | work norm (c) | |
| 27.0 : | work production factor : | |
| 1.0 : | optional: | |
| 1.0 : | optional: | |
| 108.0 : | answers: production norm: | |
| 4.0 : | combined work norm |
Testcase 4
| table 4 | Ancient Egyptian work norms for sandals | printed in tcl wiki format |
|---|---|---|
| quantity | value | comment, if any |
| 4: | testcase_number | |
| 10.0 : | work norm (a) | cutting norm is 10 sandals per one man*workday |
| 5.0 : | work norm (b) | finishing norm is 10/2 or 5 sandals per one man*workday |
| 10000000.0 : | work norm (c) | large n negates term c |
| 3.0 : | work production factor : | |
| 1.0 : | optional: | |
| 1.0 : | optional: | |
| 9.999 : | answers: production norm: | ~ 10 pairs of sandals |
| 3.333 : | combined work norm | |
| ref. Unexpected Links between Egyptian and Babylonian Mathematics, Joran Friberg |
Screenshots Section
figure 1.
References:
- A Remarkable Collection of Babylonian Mathematical Texts, Joran Friberg,
- Chalmers University of Technology, Gothenburg, Sweden
- (major work on Babylonian problems, includes combined work norm problems)
- Otto Neugebauer, Astronomical Cuneiform Texts, 3 Vols.
- Lund Humphreys, London, 1955:405,430-31.
- Otto Neugebauer, Mathematical Cuneiform Texts,
- Neugebauer includes combined work norm problems and side material.
- Bricks and mud in metro-mathematical cuneiform texts,
- Joran Friberg,
- includes combined work norm problems and necessary coefficients
- On the Alleged Counting with Sexagesimal Notation in Mathematical Cuneiform Texts,
- Joran Friberg, contains translation on combined work norm problem.
- Unexpected Links between Egyptian and Babylonian Mathematics,
- Joran Friberg, has comparison between Egyptian and Babylonian combined norm problems
- Muroi, Kazuo (1988). Inheritance problems of Babylonian mathematics.
- Historia Scientiarum , 34, 11-19
- Sumerian Construction Rates and eTCL Slot Calculator Demo Example
- Chabert, J. "Methods of False Position." Ch. 3 in A History of Algorithms: From the Pebble to the Microchip. , 1999.
- John Hannah , False position in Leonardo of Pisa's Liber Abbaci,Historia Mathematica Volume 34 issue 3 2007
- Eugene C. Boman,False Position, Double False Position and Cramer's Rule, College Mathematics Journal
- Howard Eves ,On the practicality of the rule of false position, Mathematics Teacher Volume 51
- Joy B. Easton, the rule of double false position, Mathematics Teacher Volume 60
- Vera Sanford, the rule of false position, Mathematics Teacher Volume 44 issue 5 1951
- Karine Chemla, Reflections on the World-wide History of the Rule of False Double Position, or: How a Loop Was Closed
- Thomas G. Edwards -- Using the Ancient Method of False Position to Find Solutions, Mathematics Teaching in the Middle School Volume 14 issue 4 2008
- Oneliner's Pie in the Sky
- One Liners
- Category Algorithm
- Babylonian Number Series and eTCL demo example calculator
- Brahmagupta Area of Cyclic Quadrilateral and eTCL demo example calculator
- Gauss Approximate Number of Primes and eTCL demo example calculator
- Land surveying in ancient Mesopotamia, M. A. R. Cooper
- Sumerian Approximate Area Quadrilateral and eTCL Slot Calculator Demo Example , numerical analysis
- Thomas G. Edwards, Using the Ancient Method of False Position to Find Solutions
- Joy B. Easton, rule of double false position
- Vera Sanford, rule of false position
- Taking a Weighted Average, Dr Math, mathforum.org/dr.math, dated 03/20/2003
- google <Weighted Average, Dr Math>, mathforum.org/dr.math
- Using Weighted Criteria to Make Decisions, Dr Math>, mathforum.org/dr.math, dated 07/18/2008
- google <Weighted sum product model Decision >
- harmonic mean discussed in Additional math functions
- harmonic mean discussed in Tcl Normalized Extended Benchmarks
- see arithmetic mean on tcl-wiki Stats 2011-05-22, RLE
- see similar 1/(1/nth) terms method used in
- Babylonian Combined Market Rates and eTCL demo example calculator, numerical analysis
Appendix Code
appendix TCL programs and scripts
# pretty print from autoindent and ased editor
# Babylonian Combined Work Norms Algorithm calculator
# written on Windows XP on eTCL
# working under TCL version 8.5.6 and 1.0.1
# gold on TCL WIKI, 25feb2017
package require Tk
package require math::numtheory
namespace path {::tcl::mathop ::tcl::mathfunc math::numtheory }
set tcl_precision 17
frame .frame -relief flat -bg aquamarine4
pack .frame -side top -fill y -anchor center
set names {{} { work norm (a) :} }
lappend names { work norm (b) :}
lappend names { work norm (c) : }
lappend names { work production factor : }
lappend names { optional: }
lappend names { optional: }
lappend names { answers: production norm: }
lappend names { combined work norm :}
foreach i {1 2 3 4 5 6 7 8} {
label .frame.label$i -text [lindex $names $i] -anchor e
entry .frame.entry$i -width 35 -textvariable side$i
grid .frame.label$i .frame.entry$i -sticky ew -pady 2 -padx 1 }
proc about {} {
set msg "Calculator for Babylonian Combined Work Norms Algorithm
from TCL WIKI,
written on eTCL "
tk_messageBox -title "About" -message $msg }
proc calculate { } {
global answer2
global side1 side2 side3 side4 side5
global side6 side7 side8
global testcase_number
incr testcase_number
set side1 [* $side1 1. ]
set side2 [* $side2 1. ]
set side3 [* $side3 1. ]
set side4 [* $side4 1. ]
set side5 [* $side5 1. ]
set side6 [* $side6 1. ]
set side7 [* $side7 1. ]
set side8 [* $side8 1. ]
# initialize placeholder answer
set combined_work_norm 1.
set production_factor $side4
set norm_a [/ $side1 60.]
set norm_b [/ $side2 60.]
set norm_c [/ $side3 60.]
set combined_work_norm [+ [/ 1. $norm_a ] [/ 1. $norm_b ] [/ 1. $norm_c ] ]
#set combined_work_norm [/ 1. $combined_work_norm ]
set combined_work_norm [/ 1. $combined_work_norm ]
set combined_work_norm [* $combined_work_norm 60. ]
set side8 $combined_work_norm
set side7 [* $combined_work_norm $production_factor ]
}
proc fillup {aa bb cc dd ee ff gg hh} {
.frame.entry1 insert 0 "$aa"
.frame.entry2 insert 0 "$bb"
.frame.entry3 insert 0 "$cc"
.frame.entry4 insert 0 "$dd"
.frame.entry5 insert 0 "$ee"
.frame.entry6 insert 0 "$ff"
.frame.entry7 insert 0 "$gg"
.frame.entry8 insert 0 "$hh"
}
proc clearx {} {
foreach i {1 2 3 4 5 6 7 8 } {
.frame.entry$i delete 0 end } }
proc reportx {} {
global side1 side2 side3 side4 side5
global side6 side7 side8
global testcase_number
console show;
puts "%|table $testcase_number|printed in| tcl wiki format|% "
puts "&| quantity| value| comment, if any|& "
puts "&| $testcase_number:|testcase_number | |& "
puts "&| $side1 :|work norm (a) | |&"
puts "&| $side2 :|work norm (b) | |& "
puts "&| $side3 :|work norm (c) | |& "
puts "&| $side4 :|work production factor : | |&"
puts "&| $side5 :|optional: | |&"
puts "&| $side6 :|optional: | |&"
puts "&| $side7 :|answers: production norm: | |&"
puts "&| $side8 :|combined work norm | |&"
}
frame .buttons -bg aquamarine4
::ttk::button .calculator -text "Solve" -command { calculate }
::ttk::button .test2 -text "Testcase1" -command {clearx;fillup 10. 20. 10. 27. 1. 1. 108.0 4.0}
::ttk::button .test3 -text "Testcase2" -command {clearx;fillup 10. 10. 20. 27. 1. 1. 108.0 4.0 }
::ttk::button .test4 -text "Testcase3" -command {clearx;fillup 20. 10. 10. 27. 1. 1. 108.0 4.0 }
::ttk::button .clearallx -text clear -command {clearx }
::ttk::button .about -text about -command {about}
::ttk::button .cons -text report -command { reportx }
::ttk::button .exit -text exit -command {exit}
pack .calculator -in .buttons -side top -padx 10 -pady 5
pack .clearallx .cons .about .exit .test4 .test3 .test2 -side bottom -in .buttons
grid .frame .buttons -sticky ns -pady {0 10}
. configure -background aquamarine4 -highlightcolor brown -relief raised -border 30
wm title . "Babylonian Combined Work Norms Algorithm Calculator" Pushbutton Operation
For the push buttons, the recommended procedure is push testcase and fill frame, change first three entries etc, push solve, and then push report. Report allows copy and paste from console.
For testcases in a computer session, the eTCL calculator increments a new testcase number internally, eg. TC(1), TC(2) , TC(3) , TC(N). The testcase number is internal to the calculator and will not be printed until the report button is pushed for the current result numbers. The current result numbers will be cleared on the next solve button. The command { calculate; reportx } or { calculate ; reportx; clearx } can be added or changed to report automatically. Another wrinkle would be to print out the current text, delimiters, and numbers in a TCL wiki style table as
puts " %| testcase $testcase_number | value| units |comment |%" puts " &| volume| $volume| cubic meters |based on length $side1 and width $side2 |&"
Console program for harmonic_mean
# pretty print from autoindent and ased editor
# harmonic_mean for math::stats? package
# working under TCL version 8.5.6 and eTCL 1.0.1
# console program written on Windows XP on eTCL
# gold on TCL WIKI, 2Mar2017
package require Tk
console show
package require math::numtheory
namespace path {::tcl::mathop ::tcl::mathfunc math::numtheory }
set tcl_precision 17
# adapted from tcl-wiki Stats 2011-05-22, arithmetic mean [RLE]
#
# ::math::harmonic_mean --
#
# Return the harmonic mean of two or more values
#
# Arguments:
# val first value
# args other values
#
# Results:
# mean harmonic_mean value
proc ::math::harmonic_mean {val args} {
set sum [ expr { 1./$val } ]
set N [ expr { [ llength $args ] + 1 } ]
foreach val $args {
set sum [ expr { $sum+1./$val } ]
}
set harmonic_mean [ expr { $N/$sum } ]
set harmonic_mean
}
puts " ::math::harmonic_mean ( 1 2 3 4 5 6 7 8 9 10 ) answer 3.4141715214740551 "
puts " [ ::math::harmonic_mean 1 2 3 4 5 6 7 8 9 10 ] 3.4141715214740551 " Snippet Pseudocode formula
#Pseudocode
weighted mean3 formula =( norm1 + norm2 ) / ( norm1 / rate1 + norm2 / rate2 )
set weighted_mean3 [ expr {(norm1+norm2)/((norm1/rate1)+(norm2/rate2)) }]
set weighted_mean3 [/ [+ norm1 norm2 ] [+ [/ norm1 rate1 ] [/ norm2 rate2 ]]]
set weighted_mean3 [/ [+ $norm1 $norm2 ] [+ [/ $norm1 $rate1 ] [/ $norm2 $rate2 ]]]
same result as ( delta quantity) / (delta time)
set weighted_mean4 [ expr { ( $norm2-$norm1 )/(( $norm1/$rate1 )+( $norm2/$rate2 )) } ] gold12Dec2018. This page is copyrighted under the TCL/TK license terms, this license . ---
Hidden Comments Section
| Category Numerical Analysis | Category Toys | Category Calculator | Category Mathematics | Category Example | Toys and Games | Category Games | Category Application | Category GUI |