Babylonian Combined Market Rates and eTCL demo example calculator, numerical analysis
This page is under development. Comments are welcome, but please load any comments in the comments section at the bottom of the page. Please include your wiki MONIKER and date in your comment with the same courtesy that I will give you. Aside from your courtesy, your wiki MONIKER and date as a signature and minimal good faith of any internet post are the rules of this TCL-WIKI. Its very hard to reply reasonably without some background of the correspondent on his WIKI bio page. Thanks,gold 6/2/2021
- Preface
- Introduction
- Alternate Introduction, Substitute text on Babylonian Astronomy Group Mathematicians
- Retro computing in Old Babylon Math
- Retro Computing in New Babylon
- Model the Babylonian algorithm from 4 modern gas pumps problem.
- Definitions and Derivation from Old Babylonian math
- Method of summing base_60 reciprocals.
- Problem from Two Market Rates
- Algebraic Derivations from Two Linear Equations
- Math Expressions into a TCL Procedure
- Primes on Clay Tablets
- Babylonian Market Rate Algorithm
- Importance of Explicit Instructions for Market Rates on Tablet IM31210P4
- Table 4. Reconstructed listing of Babylonian Base_60 inverse reciprocals
- Flexible Push Button Operation in TCL calculator
- Testcases Section
- Testcase 5, heavily modified script, fine and common oil & MS3895 midstages
- Testcase 6, silver= 1 (60 parts)
- Testcase 7, silver= 1 (60 parts)
- Testcase 8, silver= 1 (60 parts)
- Testcase 9, silver= 1 (60 parts)
- Testcase 10, problem MS3895 ref Friberg.
- Screenshots Section
- References:
- Pseudocode & Equations Section
- Appendix Code
- Comments Section
Preface
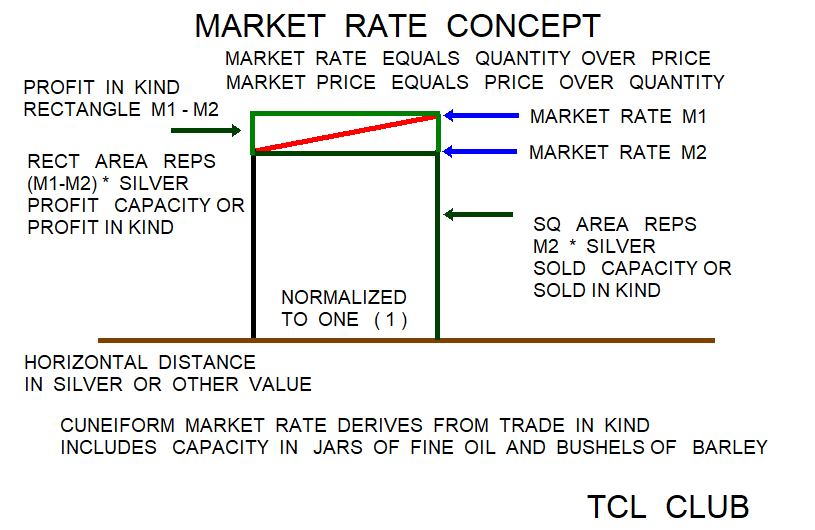
gold Here are some TCL calculations for math problems on Combined Market Rate. In modern algebraic notation, the conventional formula for combined market rate (CMR) equals N / (1/mr1 +1/mr2 +1/mr3...... +1/mr( N )), where mr are successive market rates from the first market rate mr1 to the Nth market rate. The units are not critical in the calculator internal math and any consistent input units and output units might be used like dollars to donuts.
Introduction
A number of Babylonian math problems have been found on market rates and combined market rates, ref Friberg and Proust. The cuneiform word for “market rate” was mahirum, expressed in quantity per price, or usually quantity of grain, oil, lard, or other product per shekel of silver. The market rate is the reciprocal of the market price as eval </ 1. market_price>. Here, the combined market rate of the combination of two or more market rates, effectively the reciprocal of the average price. Some of the problems seem directed towards calculating a combined market rate for a market basket of goods or stock on hand. Some of the problems are directed toward calculating profits in commodities like oil and lard from combined market rates. The Babylonian mathematicians are calculating the market prices, market rates, and unknowns in commodity markets that fluctuate in price over time. Including references to modern examples, buying different commodities and stocks at different prices over time may lead to combined market rate problems. Also, some combined market rate problems with unknowns may require solving either 1) a quadratic equation or 2) two or more simultaneous linear equations. A related math method or comparable problem type is the combined work norms, as seen in some old Babylonian math problems. Several linguists have developed alternate theories or methods on the Babylonian solutions for combined market rate. The TCL calculator appears to be working as it stands. Would like to firm up concepts with some better testcases.
In the cuneiform math problems and coefficient lists on clay tablets, there are coefficient numbers which were used in determining the amount of materials and the daily work rates of the workers. In most cases, the math problem is how the coefficient was used in estimating materials, work rates, and math problems. One difficulty is determining the effective magnitude or power of the number coefficient in the base 60 notation. In cuneiform, numbers in base 60 are written using a relative notation. For example, 20 could represent either 20*3600,20,20/60, 20/3600, or even 1/20.The basic dimensions and final tallies were presented in the cuneiform accounts on clay tablets, but some calculations, some units, some explanations, and some problem answers (aw shucks!) were left off the tablet. The Babylonians did not use algebra notation, decimal notation, or modern units, so the reader will have to bear some anachronisms in the initial pseudocode preparations and final TCL code. At least one approach for the modern reader and using modern terminology is to develop the implied algebraic equations and decimal equivalents from the cuneiform numbers. Then the TCL calculator can be run over a number of testcases to validate the algebraic equations.
Alternate Introduction, Substitute text on Babylonian Astronomy Group Mathematicians
Here in this article, the combined market rate is defined as the combination of two or more market rates, effectively the reciprocal of the average price. Some of the problems seem directed towards calculating a combined market rate or combined value for a market basket of goods or stock on hand. Very interesting in terms of the history of economics and capitol gains, as the problems suggest Babylonian interest in the overall health of the marketplace or overall value of stocks in hand. The Babylonian Astronomy Diaries record some prices of the marketplace economy and suggest these combined market rate problems were a special interest of the Babylonian Astronomy Group Mathematicians. These Babylonian Astronomy Group Mathematicians were the most advanced mathematicians in Babylon, so any insight into their mind set should be useful in historical terms.
Retro computing in Old Babylon Math
Here is suggested application and tablet presentation for a market rate problem in method of summing base_60 reciprocals. A boy buys 12 apples for 60 cents at the market. Then on his street, the boy sells 3 apples for 20 cents, 3 apples for 10 cents, and 4 apples for 30 cents. The total sales on the street were lumped as 60 cents in jeans pocket. The boy has made a profit of <expr 12-(6+4)> or 2 apples. Compute the shares for each street sale using the Babylonian method of summing base_60 reciprocals. The base_60 reciprocals are computed in <expr 60/3> as 20, <expr 60/3> as 20, and <expr 60/4> as 15. The sum of the base_60 reciprocals is <expr 20+20+15> as 55/60. Further, the base_60 reciprocal of the sum is 60/55, used as a multiplying factor. Share a is 20*(60/55) or 21.818. share b is 20*(60/55) or or 21.818, share c is 15*(60/55) or 16.36, using decimal notation here. The check answer is <expr 21.818 +21.818 +16.36 >=59.999 cents. For tablet presentation on the small hand tablets extant, the method of summing base_60 reciprocals is usually presented as 4 columns of 2 to 5 rows.
The extant hand tablets in math are small and are simply columns of numbers only, usually without headers. The TCL table format is suitable to display the mixed base_10 & base_60 numbers. In fact, the tables on clay tablets are the ancestors of the modern math tables and computer spreadsheets. To the basic core of decimal numbers, some labels and sums are added. The math tablets customarily list numbers in descending order of magnitude. In our tablet presentation, the large sale of 4 apples is listed first and not in chronological order. The larger and formal tablets may have line numbers, header labels, totals, numbers in margin, place, and signature, but not common or complete in school tablets.
| table 1 | Method of Summing base_60 Reciprocals | printed in | tcl format, mixed base_10 decimals & base_60 | ||
|---|---|---|---|---|---|
| line number | quantity | base_60 reciprocal | share | base_60 factor | comments, if any |
| 1 | 4 : | 15: | 16_22 | 60/55 | third street sale |
| 2 | 3 : | 20: | 21_49 | 60/55 | first street sale |
| 3 | 3 : | 20: | 21_49 | 60/55 | second street sale |
| 4 | 10 : | 55/60: | ~ 60 | sums | |
| 5 | year of King's victory | month 8 | day 2 | Elath the Scribe in Ishtar house | year, date,signature, and place, but not common at school |
Retro Computing in New Babylon
A fuel pump at a grocery store has 4 fuels at marked prices for the day. What is the average price and combined market rate of the 4 fuels from hand calculator and the TCL calculator? The price list has the data on low octane gas ($1.81), medium octane gas ($2.08), high octane gas ($2.33), and diesel $(2.09). The average price is eval </ <+ 1.81 2.08 2.33 2.09 > 4. > as $2.0775. The price of fuel is price over quantity as dollars per gallon. The market price of individual fuels is quantity over price as gallons per dollar. In other terms, the market price of individual fuels is the reciprocal of the price (1/price). The combined market price for the four fuels is </ 1. </ <+ </ 1. 0.5524> </ 1. 0.4807> </ 1. 0.42918 > </ 1. 0.47846> > 4. > > or 0.4813 gallons per dollar. As a check answer, the reciprocal of the combined market rate (1/0.4813) is the average price, $2.0775. Loading the reciprocals, the TCL calculator returned an average price of 2.0818 and combined_market_price of 0.4803. Given the inverse relationships of price, the alternate of loading the straight prices into the calculator returns price over quantity as 0.4852 and average market price as 2.061. The alternate of loading market prices is not an intended use of the calculator, but is an alternate check on the calculator.
Model the Babylonian algorithm from 4 modern gas pumps problem.
1. The Setup or initial stage for Babylonian algorithm of summing base_60 reciprocals. The gist of problem is how many times the shares of four unit prices can be purchased with the available dollars in pocket (60 dollars). The 4 pump prices in gallons per dollar and “1” equals (implied) 60 dollars in pocket . The Babylonian scribe mathematician uses “1” meaning equivalent 60 parts, which falls out to 60 dollars in pocket in this problem. The set of 4 modern pump prices was < 1.81 2.08 2.33 2.09 >.
On a tablet, the usual givens are the available silver, as 1 or more than one, and the market rates of 2 to 7 quantities per silver. The modern gas pumps measure gallons per dollar ($value), so market rates are reconstructed as Base_60 reciprocal pairs or inverses, expr { $value / 60. }. The Bablylonian mathematicians used a standard table of Base_60 reciprocal, which is reconstructed on this wiki page.
2. Midstage or follow up calculations, sum unit costs. The $sum_unit_prices of the 4 pump prices expr { 1.81 + 2.08 + 2.33 + 2.09}, 8.31. The average pump price is eval </ <+ 1.81 2.08 2.33 2.09 > 4. > as $2.0775. The set of 4 market rates using Babylonian Base_60 inverses was < 33.14917 28.8461 25.75107 28.7081 > . The average market rate is eval </ <+ 33.14917 28.8461 25.75107 28.7081 > 4. >, 29.11361 decimal. The average market rate using the inverse of the average market price is expr { 60./ 2.0775 }, 28.8808 . Here, market rate from the pump reading equals the Babylonian Base_60 inverse of the market price.
3. Final stage, sum the 4 shares. The scale factor for the shares is expr { 60./8.31} , 7.22021 . Share a equals expr { 1.81* 7.22 } 13.0682, decimal Base_10. Share b equals expr { 2.08* 7.22 }, 15.0176, decimal Base_10. Share c = expr { 2.33* 7.22 } 16.8226, decimal Base_10. Share d = expr { 2.09 * 7.22 } 15.0897, decimal Base_10.
4. check results. The total shares are expr { 13.0682 + 15.0176 + 16.8226 + 15.0897 },59.9981, and rounds to 60. The average share is expr { (13.0682 + 15.0176 + 16.8226 + 15.0897)/4. }, 14.999525 and rounds to 15. For alternate calculations, the average share is expr {60/4.}, 15.0. Also check that the Base_60 reciprocal pairs are expr { $MR1* $P1} = 60, save the exception for 1, which is the reciprocal pair of itself.
5. Extension on more available silver. Instead of “1” or 60 for the available silver, the available silver is given 1_1_1, sexagesimal or expr { 1*3600 + 1*60 +1 }, 3661 decimal. The general equation for the shares would be $available_silver = $false_share * $unit_price_1 + $false_share * $unit_price_2 + $false_share * $unit_price_3 + $false_share * $unit_price_4. Combining the 4 unit prices and transposing, the $false_share = $available_silver / ( $unit_price_1 + $unit_price_2 + $unit_price_3 + $unit_price_4 ). With further reduction, $false_share = $available_silver / ( $sum_unit_prices ). Subbing in this extension, the $sum_unit_prices equals expr { 1.81 + 2.08 + 2.33 + 2.09}, 8.31. The new $false_share = expr { 3661 / 8.31 }, 440.5535. Multiplying each unit price by the new false share of 440.5535, the set of new shares would be { 797.4018 916.3512 1026.4896 920.7568 }. The check sum shares would be expr { 797.4018 + 916.3512 + 1026.4896 + 920.7568 }, 3660.9994, rounds to 3661.
gold 6/2/2021. Using some alternate calculations on market rates, I posted a Math proc Template called ::math::quantity_into_ratios on the wiki. For the initial available silver of 60 pieces, eval < ::math::quantity_into_ratios 60 1.81 2.08 2.33 2.09 > returns shares < 13.0685 15.0180 16.8231 15.0902 >. For the extension with available silver of 3661 pieces, eval < ::math::quantity_into_ratios 3661 1.81 2.08 2.33 2.09 > returns 797.4019 916.3513 1026.4897 920.7569 > . This TCL subroutine routine seems robust and should be able to handle most of the market rate problems thrown by the the shades of the Babylonian mathematicians.
| Table 12 for 4 modern gas pumps | printed in | tcl wiki format | |||
|---|---|---|---|---|---|
| *** setup or initial stage for Babylonian algorithm of summing base_60 reciprocals *** | |||||
| given, available dollars in pocket | 60 | B. uses “1” meaning equivalent 60 parts | |||
| given, 4 unit prices | < 1.81 2.08 2.33 2.09 > | reading from 4 pumps | |||
| *** midstage or follow up calculations, sum unit costs | |||||
| quantity | value | 60 / value | comment, if any | ||
| conventional id | reconstructed tablet value | base_60 reciprocal | market rates not on modern pumps, only prices | ||
| market rate 1 | 33.1492 | 1.81 | 13.0685 | 7.2202 | low octane gas($1.81) |
| market rate 2 | 28.8461 | 2.08 | 15.018 | 7.2202 | medium octane gas ($2.08) |
| market rate 3 | 25.7510 | 2.33 | 16.8230 | 7.2202 | high octane gas ($2.33) |
| market rate 4 | 28.7081 | 2.09 | 15.0902 | 7.2202 | diesel fuel $(2.09) |
| sum unit prices | 8.31 | sun_prices =expr { 1.81 + 2.08 + 2.33 + 2.09 },8.31 | |||
| scale_factor | 7.22 | scale_factor = { 60./8.31 } , 7.22 | |||
| *** final stage , sum shares *** | |||||
| share a | 13.0682 | share a = expr { 1.81* 7.22 }13.0682, decimal Base_10 | |||
| share b | 15.0176 | share b = expr { 2.08* 7.22 }15.0176, decimal Base_10 | |||
| share c | 16.8226 | share c = expr { 2.33* 7.22 }16.8226, decimal Base_10 | |||
| share d | 15.0897 | share d = expr { 2.09 * 7.22 }15.0897, decimal Base_10 | |||
| sum shares | 60.0 | $sum_shares = expr { 13.0685+15.018 +16.823+15.0902}, 59.9997 | |||
| *** extension, new available silver *** | |||||
| new given, available dollars in pocket | 3661 | B. uses “1” meaning equivalent 60 parts | |||
| given, 4 unit prices | < 1.81 2.08 2.33 2.09 > | same reading from 4 pumps | |||
| sum unit prices | 8.31 | sun_prices = expr { 1.81 + 2.08 + 2.33 + 2.09 },8.31 | |||
| scale_factor | 440.5535 | scale_factor = expr { 3661 / 8.31 }, 440.5535 | |||
| sum shares | 3661.0 | $sum_shares = expr { 797.4018 + 916.3512 + 1026.4896 + 920.7568 }, 3660.9994 |
Definitions and Derivation from Old Babylonian math
There are Babylonian texts where two market rates for different quantities are straight added or subtracted. The term for market rate depending on the cuneiform language are mahirum or ganba (KI.LAM). In one problem, the market rate for oil was 8 silas per shekel and 10 sila per shekel; the given difference or profit was 2 sila per shekel. However, there was lack of a small currency in Mesopotamia. Most transactions in Ancient Mesopotamia were in kind and profits were based on the stock, oil, or grain on hand. or effectively the accounting value in barley measures. Lets construct a problem where the reciprocals of prices are easy fractions in base 60. In the constructed problem using a barrel (beriga) of 60 silas ( 1 sila=1 liter) , the merchant brought sesame oil for 12 silas per shekel (mr1) and sold for 10 sila per shekel (mr2) ; the given rate difference was {expr mr2-mr1} or 2 sila per shekel. The original price was 1/mr1, 1/12, or 4/60 shekel per sila. The selling price was 1/mr1, 1/10, or 6/60 shekel per sila. The merchant made a profit of {expr 6/60-4/60}, or 2/60 shekels per sila. Using the modern method of price calculation and following the Friberg derivation, Profit P1 equals Barrel_Capacity * (sell_Price_2 – buy_Price_1), Profit P1 equals Barrel_Capacity * (1/market_rate2 – 1/market_rate1). The profit on a barrel of sesame oil would be P1 = Barrel_Capacity*( 1/m2-1/m1), {expr 60 * (6/60-4/60)}, or 2 shekels. Using the original market rate, the profit can be expressed in kind as {expr 2*12 } or 24 sila of sesame oil.
Now as life complicates the affairs of the Babylonian merchant, suppose the merchant carries stocks of fine sesame oil and common palm oil, but deals with no silver currency. Now, profits must be measured in kind, oil stocks, or accounting values. There would be 4 market rates (m1&m2 for fine oil, mr1&mr2 for common oil. Lets keep the same market rates for the sesame oil as m1s of 12 and mr2s of 10, but add market rates for the common palm oil as mr1c of 15 and mr2c of 20. Considering the original market prices, the market price ratio of fine oil over common oil would be (1/mr1s)/(1/mr1c) or { expr (1./12)/(1./15)} , 1.25 decimal or 75/60 as a base 60 fraction. Using the same barrel for the common oil, the merchant found a loss of {expr 60*(20/60-15/60) }, or 5 silas of common oil. The loss was equivalent to {expr 5*60/75 } or 4 silas of fine oil. The Babylonians did not use positive and negative numbers in the tablet era, but the tablets do record equivalent of surplus product or deficit product as commonly oil or barley.
Method of summing base_60 reciprocals.
Given the multiple market rates, compute the shares for each line using the Babylonian method of summing base_60 reciprocals. The given rates are < 3 4 5 6 > and posted as a column, as numbers separated by ruled horizontal and vertical lines. The TCL math expressions here are pastable into the Easy Eye Calculator console. While the rates are given as bare numbers, the rates could be dressed up from abstract math. The rates could be treated as rates in kind or fish in the basket, < 3_red_fish 4_green_fish 5_blue_fish 6_yellow_fish > . Continuing, the sum of the market rates is <expr 3+4+5+6 > as 18 fish in the basket. The base_60 reciprocals are computed in <expr 60/3> as 20, <expr 60/4> as 15, <expr 60/5> as 12, and <expr 60/6> as 10. The base_60 reciprocals are the price for each line or kind (type) of fish in the basket, <prices red_fish =20 green_fish=15 blue_fish=12 yellow_fish=10 > . The sum of the base_60 reciprocals is <expr 20+15+12+10> as 57/60. The sum of the base_60 reciprocals is the sum of the prices for every fish type in the basket and the total price for each kind (type) of fish is 57/60. The average price of each kind of fish is <expr (57/60.)/4. > or 0.2375 decimal fraction or rounded 14/60 gin or shekel. As a check or alternate calculation, the average price of each fish type is <expr (20+15+12+10)/4> over 60 units of coin is 14/60. Further, the base_60 reciprocal of the sum is 60/57, used as multiplying factor and kept as rational integer fraction. The correct calculation of the sum of the base_60 reciprocals is the key to the market rate problem. Most school tablets have posted in the top margin as well as listed in a column and rows. Share a is <expr 20.*(60./57.)> or 21.052; share b is <expr 15.*(60./57.)> or 15.789; share c is <expr 12.*(60./57.)> or 12.631; share d is <expr 10.*(60./57.)> or 10.526, using decimal notation here. The check answer is <expr 21.052+15.789+ 12.631+10.526 > equals 59.999 decimal units of coin.
Now the next complication is market rate problems where the total price from rates or kind types is not one silver gin, shekel, dollar etc, but usually greater then one. There are several methods for this calculation, including the false position method known to the Babylonian mathematicians. But in some Babylonian math tablets, the preceding algorithm or repetitive calculations are forked with an additional step in the midstage. Continuing from above and inserting a new multiplication factor, the assigned new price might be 60800. The new factor would be expr 60800/57 or 1066 as 17_46_ 40 in base_60. Rounding and artifacts in base_60 gives <expr 17*60+46+40/60> as 1066.666 . Share a is <expr 20.*1066.666> or 21333.32; share b is <expr 15.*1066.666> or 15999.99; share c is <expr 12.*1066.666> or 12799.991; share d is <expr 10.*1066.666> or 10666.66, using decimal notation here. The check answer is <expr 21333.32+15999.99+ 12799.991+10666.66 > equals 60799.960 decimal units for the new total price in kind.
| table 2 | Method of Sum of base_60 reciprocals | printed in | tcl format | ||
|---|---|---|---|---|---|
| line number | quantity | base_60 reciprocal | share | base_60 factor | comments, if any |
| ___ | ______ | _______ | ______ | 60800 | top margin ,total price of kind types, possibly by teacher? on homework tablet |
| 1 | 3 : | 20: | 21333.32 | 60800/57 | first rate, mixed base_10 and base_60 |
| 2 | 4 : | 15: | 15999.99 | 60800/57 | second rate |
| 3 | 5 : | 12: | 12799.991 | 60800/57 | third rate |
| 4 | 6 : | 10: | 10666.66 | 60800/57 | fourth rate |
| 5 | 18 : | 57/60: | ~ 60800 | sums | |
| 6 | year of king's ship | month 10 | day 8 | GinGin the Junior Scribe at Annu Temple | date and signature |
What is the source of the new high prices? The short answer says “fish is fish and gold is gold”. The Babylonian merchants dealt in silver bars, gold ingots, gold jewelry, valuable iron armor and weapons, and costly tin ingots for making bronze. The original problems here dealt with one silver gin, but the scale of value in silver goes from one grain (0.15 gram) of silver, one silver gin (9 gm), one silver mana (497.7 gm), and one talent (30000 gm). The relative values of metals in different eras comes into play; also. During the classic Sumerian eras, tin and iron was much more valuable than silver, including uses for jewelry, ornamentation, and artworks. Ancient Mesopotamia was poor in metals and generally these “new” metals and ores introduced into the ancient economy came from great distances as far as modern India, Spain, and Egypt.
Lets try inserting another and new multiplication factor in the midstage of the algorithm. In order of magnitude, the new value scale should be compatible with the value of a silver mana (497.7 gm, 55 gin). With 5 prices in kind, the new total price in kind might be scaled to <expr 5*55>, 275 rounded to 600 for ease of factoring in base_60. The new factor would be expr 600/57. Share a is <expr 20.*10.526> or 210.519; share b is <expr 15.*10.526> or 157.89; share c is <expr 12.*10.526> or 126.312; share d is <expr 10.*10.526> or 105.259, using decimal notation here. The check answer is <expr 210.519+157.89+ 126.312+105.259 > equals 599.98 decimal units for the new total price in kind.
Problem from Two Market Rates
| Table 12, YBC4698 for fine and common oil | printed in | tcl wiki format | |||
|---|---|---|---|---|---|
| *** setup or initial stage *** | comments, if any | ||||
| given, 1 silver shekel available in pocket | 60 | B. uses “1” meaning equivalent 60 parts | |||
| 2 market rates | < 3.0 12.0 > | on tablet | |||
| 2 unit costs | < 20.0 5.0 > | reconstructed | |||
| *** midstage or follow up calculations, sum unit costs | |||||
| conventional id | reconstructed tablet value | reconstructed | share | scale_factor | |
| market rate 1 | 3.0 : | 20.0 | 48.0 | 2.399 | |
| market rate 2 | 12.0 : | 5.0 | 12.0 | 2.399 | |
| scale_factor | 2.399 | scale_factor = expr { 60/(20.+5.)} | |||
| *** final stage , sum shares *** | |||||
| share a | 48.0 | ||||
| share b | 12.0 | ||||
| sum_shares | 60.0 | sum_shares = expr { 60/(48.+12.)} | |||
| Note | ref Friberg commentary on YBC4698 , | A Remarkable Collection of Babylonian Mathematical Texts. | |||
| Note | The tablets use Base_60 fractions | But the TCL calculations throw out modern Base_10 decimals |
Algebraic Derivations from Two Linear Equations
Following the Friberg derivation and modern algebra, 1) Price P1 equals market_price_1 and 2) Price P2 equals market_price_2. From the definitions above, Price P1 equals (1/market_rate_1) and Price P2 equals (1 / market_rate_2). For the relationship of P1 over P2, divide the equation as 1) over 2) which results in P1/P2 = (1/market_rate_1)/(1 / market_rate_2). Simplify terms as equation 3) P1 = (market_rate_2 / market_rate_1) * P2. Alternately, equation 4) would be P2= (market_rate_1 / market_rate_2)*P1, note inverse relationship. In terms of modern algebra, the Babylonian problem has at least one linear equation or linear relationship in equation 3) between P1 and P2, using the given market rates m1 and m2. In some Babylonian problems but not all, there is an additional statement that the Babylonian merchant brought equal amounts of P1 at rate m1 and P2 at rate m2 for one unit of currency. The given unit was a silver gin or shekel (8.4 gm), equivalent 1/60 of silver mina (504 gm silver). In the math problems, the silver shekel was also broken down into 1/60 units as a silver fraction or silver penny. The equation setup is 5) total cost or 1 gin equals P1 + P2 or 1 = P1 + P2. Substituting the third equation 3) into the fifth equation 5), 1 = (market_rate_2 / market_rate_1) * P2 + P2. P2 = 1 / (market_rate_2 / market_rate_1 + 1.). Also, there are the findings that 6) P1 = 1-P2 or 7) P2 = 1-P1, in this case where total_cost equals 1. Equations 1) to 7) are the generic equations for a modern algebraic solution of the Babylonian market rates using 2 linear equations. However, there is no guarantee or problem solution in the texts of what method that the Babylonian mathematicians actually used.
In modern algebraic notation, the conventional formula for combined market rate (cmr) equals N / (1/mr1 +1/mr2 +1/mr3...... +1/mr( N )), where mr are successive market rates from the first market rate mr1 to the Nth market rate. In electrical engineering, the algebraic formula for joint resistance of 2 or more parallel resistors is exactly the same. The conventional formula for joint resistance a) rp = N / (1/r1 +1/r2 +1/r3...... +1/r( N )), where the joint resistance is dubbed jp and r()'s are successive parallel resistors from the first resistor r1 to the Nth resistor. If the reader will pardon a change in variables for joint resistance rp and resistors 1 to N in parallel (r1,r2,r3 etc), some convenient formulas for parallel resistors and other quantities can be developed to match old textbooks, including the clay tablets. This discussion covers parallel resistors greater than zero and specifically excludes trivial cases of either rp, r1, or r2 = 0. For 2 resistors in parallel, the base equation is b) 1/rp =1/r1 + 1/r2. Inverting both sides and combining terms on the right gives c) rp = (r1*r2)/(r1+r2). Solving for r1 and r2 alternately presents d) r1= (r2*rp)/(r2-rp) and 4) r2= (r1*rp)/(r1-rp). For three resistors, the base equation is e) 1/rp =1/r1 + 1/r2 + 1/r3. Inverting both sides and combining terms on the right gives f) rp = (r1*r2*r3)/(r1*r2+r1*r3+r2*r3). For rules of thumb, the joint resistance is generally lower than either r1 or r2 and following from this conclusion, certainly lower than the average of r1 & r2, excluding r's = 0 cases or shorts. These parallel resistor formulas can be packaged into one-liner procs and were used to check the calculations and to develop testcases for combined market rates.
Since the above parallel resistor formulas are old staples in the biz, now one can swap and uncloak variables. Equation c) becomes 9) cmr= (mr1*mr2)/(mr1+mr2). Equation d) above becomes 10) mr1= (mr2*cmr)/(mr2-cmr). Equation e) above becomes 11) mr2= (mr1*cmr)/(mr1-cmr).
Math Expressions into a TCL Procedure
For evaluation of the market rates in tablet YBC 4698 (pm. 3, Proust) from the generic linear solution, the entries might be mr1=3 sila, mr2=12 sila, and total_price=1 gin. P2= (1/5) gin, or P2=12/60 gin as a base 60 fraction. P1= 4/5 gin, or P1=48/60 gin as a base 60 fraction. As a math check, the sum of 12/60 plus 48/60 = 1. It is suggested that the modern linear solutions are within +- 20 percent of the possible Babylonian solutions and base 60 round-off, but the complete answer was not found or given in the texts. From the Friberg and Proust paper(s), there is reason to believe the answer was not given, because the solution was inherent or commonly referenced to possible metrological tables or commodity price/rate standards (including law of Eshnunna, see Friberg). The Babylonians mostly used market rates and integer ratios for m1/m2 as limited integers under 30 (in base 60). A table of generic linear solutions from rational integer fractions could be constructed using a TCL subroutine. And if the right Babylonian math tablet could be found …
Now with the generic linear solution for a market rate problem, approximate TCL eval expressions, and the Friberg/Proust translations, we are better prepared to generate the market rate method and math expressions into a TCL subroutine using base 10. Joran Friberg has translated MS3895, a market rate problem which has 24 readable lines. In the MS3895, the Babylonian method is using math expressions in base 60, which the generic linear solution did not use. For example, the Babylonian method in tablet MS3895 is taking squares and there are other market rate expressions from other tablets, which are equivalent to (mr1+mr2)/2, (mr1-mr2)/2,((m1-m2)/2)**2, and mr1*mr2, ref Friberg and Proust. This report will use the modern conventions of algebraic notation , which can be entered into pseudocode or TCL expressions. The math expression (mr1 + mr2)/2 is a conventional average of two rates. The math expression (mr1 - mr2)/2 is a conventional half the difference of two rates. The math expression ((mr1 – mr2)/2)**2 is a square of half the difference of two rates. The math expression mr1*mr2 is the product of two rates, which are treated as an area in some texts. Some of these math expressions appear in Babylonian trapezoid formulas and possibly these market rate methods were adapted from trapezoid or trapezoidal prism formulas. While perhaps redundant to the Friberg and Proust findings in base 60 already, the intent to evaluate the alternate path of the MS3895 midstages and throw out the decimal base 10 expressions into a spreadsheet or table format for study. Since there are some tablets with incomplete or unreadable lines, there might be some advantage in reconstructing the decimal math expressions in the problem set up (program entry), midstage, and answers (program output).
Primes on Clay Tablets
In some sense, the Plimpton 322 clay tablet is also generating a set of prime numbers in the available triplet collection on the clay tablet. The Babylonian regular numbers in base_60 between 0 and 60 have a limited set of triplets that satisfy 1< X-1/X < 1+sqrt(2) which appears to be the role of Plimpton 322. The limit 1< X-1/X < 1+sqrt(2) may explain the 1<X<2 limit on the Late Babylonian many place reciprocal tablets.
While the modern mathematicians are trying to find prime numbers in base_10, the Babylonian mathematicians in base_60 were trying to avoid prime numbers. The primes are the Achilles heel of the Babylonian multiplication system using reciprocals in base_60. The number set in the sequence {7 11 13 14} was especially foul to the Babylonian multiplication system, although the Babylonian mathematicians did use the set {7 11 13 14} in arithmetic or "advanced non-standard" calculations. One trick that the Babylonian mathematicians was to multiply an odd number or prime number by 2 or 3 at one early stage of the calculations and then divide out respectfully the 2 or 3 at a later stage of the calculations. For example, 7*2 converts an overtly prime number to a number 14 with factors 2*7. However, this multiplication trick with 2 or 3 as factors is confusing in the extant school and library tablets, so sometimes the modern reader is stressed by a missing factor of 2/3 after corrupted or dropped tablet lines.
| table 1 Percentage Primes in Modern Base_10 and Babylonian Base_60 | printed in | tcl wiki format | |
|---|---|---|---|
| quantity | value | value | comment, if any |
| set_number: | percent of prime numbers in set | percent primes in set of 10 over / set of N | |
| set 10 : | 44.44 | 1.0 | Modern base_10 |
| set 20 : | 42.10 | 1.05 | Archaic IndoEuropean base_20 |
| set 30 : | 34.48 | 1.28 | |
| set 40 : | 30.76 | 1.44 | |
| set 50 : | 30.61 | 1.45 | |
| set 60 : | 28.81 | 1.54 | Babylonian base_60 |
| set 70 : | 27.53 | 1.61 | |
| set 80 : | 27.84 | 1.59 | |
| set 90 : | 26.96 | 1.64 | |
| set 100 : | 25.25 | 1.76 | |
| set 110 : | 26.60 | 1.67 | |
| set 120 : | 25.21 | 1.76 |
;# using TCLLIB math prime subroutines
;# COUNTING SETS OF 10 WITH PERCENTAGE OF PRIMES RELATIVE TO BASE_10
puts "%| set_number:|percent of prime numbers in set | |%"
foreach value {10 20 30 40 50 60 70 80 90 100 110 120} {
puts "&| set $value :|[ expr { [llength [ primesLowerThan [- $value 1 ] ]]*100./ [- $value 1 ] }] |[ expr { ([llength [ primesLowerThan [- 10 1 ] ]]*100./ [- 10 1 ] )/( [llength [ primesLowerThan [- $value 1 ] ]]*100./ [- $value 1 ]) }] | |&" }Babylonian Market Rate Algorithm
Here in this article, the combined market rate is defined as the combination of two or more market rates, effectively the reciprocal of the average price. Some of the problems seem directed towards calculating a combined market rate or combined value for a market basket of goods or stock on hand. Very interesting in terms of the history of economics and capitol gains, as the problems suggest Babylonian interest in the overall health of the marketplace or overall value of stocks in hand. The Babylonian Astronomy Diaries record some prices of the marketplace economy and suggest these combined market rate problems were a special interest of the Babylonian Astronomy Group Mathematicians. These Babylonian Astronomy Group Mathematicians were the most advanced mathematicians in Babylon, so any insight into their mind set should be useful in historical terms.
Use the set {7 11 13 14} which contains primes for the market rate problem, but also include the Babylonian algorithm of summing Base_60 reciprocals in the midstage or followup calculations. The correct calculation of the sum of the base_60 reciprocals is the key to the market rate problem. Most school tablets have the sum of the base_60 reciprocals posted in the top margin as well as listed in a column and rows. The sum of the base_60 reciprocals is <expr 8.5714 + 5.4545 + 4.6153 + 4.2857 > as 22.9/60. The sum of the base_60 reciprocals is the sum of the prices for every type in the basket and the total price for each kind (type) is 22.9/60. Here the sum of shares is set to 60 pieces. Share a is <expr 8.5714*(60./22.9 )> or 22.4578 ; share b is <expr 5.4545*(60./22.9 )> or 14.2912 ; share c is <expr 4.6153*(60./22.9)> or 12.09248 ; share d is <expr 4.2857 *(60./22.9)> or 11.2289 , using decimal notation here.
| table 2 Using primes in Market Rate Problem | Babylonian algorithm of summing base_60 reciprocals | printed in | tcl wiki format | |
|---|---|---|---|---|
| quantity | market rate ( value) | market price ( 60 / value ) | 1.0 / value | comment, if any |
| conventional id | tablet value | base_60 reciprocal | base_10 reciprocal | TCL expression |
| market rate 1 | 7 | 8.5714 | 0.14285 | expr { 60. / 7} |
| market rate 2 | 11 | 5.4545 | 0.09090 | expr { 60. / 11} |
| market rate 3 | 13 | 4.6153 | 0.07692 | expr { 60. / 13} |
| market rate 4 | 14 | 4.2857 | 0.071428 | expr { 60. / 14} |
| sum base_60 reciprocals | 22.9269 | sum base_60 = expr {8.5714 + 5.4545 + 4.6153 + 4.2857 } | ||
| sum base_10 reciprocals | 0.382098 | sum base_10 = expr {0.14285 + 0.09090 + 0.07692+ 0.071428 } | ||
| *** | midstage or follow up calculations for | Babylonian algorithm of summing base_60 reciprocals | *** | |
| *** | midstage or follow up calculations | beware, some tablets have an algorithm fork here | *** | |
| *** | >>if<< sum base_60 reciprocals greater than 60 pieces | *** | ||
| share a | 22.4578 | expr 8.5714*(60./22.9 ) | ||
| share b | 14.2912 | expr 5.4545*(60./22.9 ) | ||
| share c | 12.09248 | expr 4.6153*(60./22.9) | ||
| share d | 11.2289 | expr 4.2857 *(60./22.9) | ||
| *** | final stage or follow up calculations for | Babylonian algorithm of summing base_60 reciprocals | *** | |
| *** | this was the proof that calculations were done correctly, | but not included on some tablets. | *** | |
| estimated total shares < a+b+c+d> | 60.07038 | total shares = expr { 22.4578 +14.2912 + 12.09248 + 11.2289 } | ||
| average share per entry for < a+b+c+d> | 15.0 | average share per entry = expr {60. /4}, maybe where 15 comes from on tablet? |
For a check on the TCL calculator algorithm, a combined work norm was calculated in several ways using hand calculations, TCL template routines, and the Babylonian algorithm of summing Base_60 reciprocals. A combined work norm was calculated using 3 work norms < 20,10,6+40./60> volume shekels per day with the given answer as 10 volume shekels per day. The combined work norm can be calculated alternately from the combined market rate methods and include the Babylonian algorithm of summing Base_60 reciprocals. The hand calculation was expr 3/(1/20.+1/10.+1/(6+40./60)) = 10 (ref. modern definition of harmonic means). The TCL template routine for combined market rate returns < ::math::combined_market_rate 20. 10. 6.666 > equals market rate? 10.0 rounded.
| table 3 | combined work norm | printed in | tcl wiki format | |
|---|---|---|---|---|
| quantity | market rate ( value) | market price ( 60 / value ) | 1 / value | comment, if any |
| conventional id | tablet value | base_60 reciprocal | base_1 0 reciprocal | |
| work rate norm 1 | 20 | 3.0 | 0.05 | norm 1 = expr {60./20} |
| work rate norm 2 | 10 | 6.0 | 0.1 | norm 2 = expr {60./10} |
| work rate norm 3 | 6.666 | 9.0 | 0.15 | norm 3 = expr {60./6.666} |
| sum base_60 reciprocals | 18. | sum = expr { 3+6+9.} | ||
| sum base_10 reciprocals | 0.30 | sum = expr { 0.05+0.1+ 0.15 } | ||
| *** | midstage or follow up calculations for | Babylonian algorithm of summing base_60 reciprocals | *** | |
| *** | midstage or follow up calculations | beware, some tablets have an algorithm fork here | *** | |
| share a | 10. | share a = expr { 3.0 * (60./18. ) } | ||
| share b | 20. | share b = expr { 6.0 * (60./18. ) } | ||
| share c | 30. | share c =expr { 9.0 *(60./18. ) } | ||
| estimated total shares < a+b+c> | 60. | total shares = expr { 10 + 20 + 30 } | ||
| average share per entry for < a+b+c> | 20. | average share = expr { ( 10 + 20 + 30 ) / 3. } |
puts "%|table 6 |printed in| tcl wiki format|% "
puts "&| quantity| 60 / value| 1/ value|comment, if any|& "
puts "&| entry |percent of prime numbers in set | |&"
foreach value {1.81 2.08 2.33 2.09 } {
puts "&| $value | [/ 60. $value ] |[/ 1. $value ] | |&" }
foreach value {7 11 13 14 } {
puts "&| $value | [/ 60. $value ] | [/ 1. $value ] | |&" } Joran Firberg provided some commentary on 2 market rate problems on tablet, MS28302a and MS28302b, ref Friberg, A Remarkable Collection of Babylonian Mathematical Texts. The preparation for the MS28302a problem was evaluation of { 1.0 + 30/60. +20./60 + 15/60. }, reduction to { 1.0 + 1.+ 5/60. }, and sum = 2+5/60. The solution was base_60 reciprocal as expr 60. /(2+(5./60)) >> 28.7999 or 28+48/60. The problem 2a shows some of the quirks of the Base_60 system in that Babylonian mathematicians jumped around 1=60=1, the reciprocal inverse of 1 was expr {1/1.} or 1, and did not use zero’s. The first inverse in the problem 2a was (1/1.) while other three inverses could be handled expr { 60. / N }. The solution for the MS 2830 § 2b problem was expr 60/64.*60. = 56.25 or 56+15/60. Its clear that the TCL market rate template probably could use some exception handling for one’s, zero’s, and null’s.
| Table 4 for problem MS28302a | printed in | tcl wiki format | ||
|---|---|---|---|---|
| quantity | market rate ( value) | market price ( 60 / value ) | comment, if any | |
| conventional id | tablet value | base_60 reciprocal | ||
| market rate 1 | 1 | 1.0 | 28+48/60. | 28+48/60. |
| market rate 2 | 2 | 30.0 | 14 +24/60. | 28+48/60. |
| market rate 3 | 3 | 20.0 | 9+36/60. | 28+48/60. |
| market rate 4 | 4 | 15.0 | 7+12/60. | 28+48/60. |
| sum | 2+5/6 | { 1.0 + 30/60. +20./60 + 15/60. }= { 1.0 + 1.+ 5/60. }, sum = 2+5/60 | ||
| sum | 60. | sum = expr { 28+48/60. +14 +24/60. + 9+36/60. +7+12/60.} | ||
| share a | 28+48/60. | share a = expr { 1.0 * (60./(2+5./60) ) } , 28.7999 | ||
| share b | 14 +24/60. | share b = expr { 1.0 * (60./(2+5./60) ) }, 14.39999 | ||
| share c | 9+36/60. | share c = expr { 1.0 * (60./(2+5./60) ) },9.6 | ||
| share d | 7+12/60. | share d = expr { 1.0 * (60./(2+5./60) ), 7.199999 | ||
| Note | ref Friberg commentary on tablet MS28302a, | A Remarkable Collection of Babylonian Mathematical Texts. | ||
| Note | The tablets use Base_60 fractions | But the TCL calculations throw out modern Base_10 decimals |
| Table 5 for problem MS28302b | printed in | tcl wiki format | ||
|---|---|---|---|---|
| quantity | market rate ( value) | market price ( 60 / value ) | comment, if any | |
| conventional id | tablet value | base_60 reciprocal | ||
| market rate 1 | 2. | 30.0 | 56+15/60 | |
| market rate 2 | 3. | 20.0 | 56+15/60 | |
| market rate 3 | 15. | 4.0 | 56+15/60 | |
| market rate 4 | 6. | 10.0 | 56+15/60 | |
| sum base_60 reciprocals | 64.0 | sum = expr {30.0 + 20.0+ 4.0 + 10.0 } | ||
| combined market rate solution | 56+15/60 | expr 60/64.*60. = 56.25 or 56+15/60 | ||
| share a | 28+7/60. +30/3600 | share a = expr { 30.0 * ((56+15/60.)/ 60. ) }, 28.125 | ||
| share b | 18+45/60. | share b = expr { 20.0 * ((56+15/60.)/ 60. ) }, 18.75 | ||
| share c | 3+45/60. | share c = expr { 4.0 * ((56+15/60.)/ 60. ) },3.75 | ||
| share d | 9+22/60. +30/3600. | share d = expr { 10.0 * ((56+15/60.)/ 60. ) }, 9.375 | ||
| Note | ref Friberg commentary on tablet MS28302a, | A Remarkable Collection of Babylonian Mathematical Texts. | ||
| Note | The tablets use Base_60 fractions | But the TCL calculations throw out modern Base_10 decimals |
Importance of Explicit Instructions for Market Rates on Tablet IM31210P4
Joran Firberg provided some commentary on a market rate problem on tablet IM31210P4 and included preparatory comments on more complete features of tablet MS2299, ref Friberg, A Remarkable Collection of Babylonian Mathematical Texts. The tablet MS2299 was used as the model problem in the Friberg commentary. Only the midstage calculations were legible on tablet IM31210P4, but important lexical ques and numbers were preserved in the midstage calculations. The preparation for the IM31210P4 problem was summing the costs, evaluation of expr { ( (30./60) + 2. + ( 1.+20./60) + (45./60.) ) } , and sum of costs = 4.5833 decimal in grain units. The solution was base_60 as adding total shares to 1_31_40 sexagesimal. Firberg gives the scale factor for the shares as 1_31_40 / 4_35 sexagesimal, 20. Decimal would be expr { (1 + 31/60. + 40./3600) /(4.+35./60) }, 0.3333 decimal translates to 1/3 or 20/60.
The setup or initial stage of the market rate problem usually gives two to seven market rates. The reciprocal of a market rate is supposed to be the Base_60 reciprocal or inverse of of the market price. There appear to be two types of midstage calculation. If the sum of the prices equals one silver shekel, or really 60 silver pennies, then the scale factor is (total price (1)) / ( sum prices ). If the sum of the prices equals more than one in total commodity, then the scale factor is calculated differently (total price (>> 1)) / sum prices ) . The solution was base_60 as either adding total shares up to 1 (60) sexagesimal or else adding total shares to more than one (>> 1) in total commodity. Usually the total shares as 1 or more were a given, sometimes noted as one silver shekel or more than one in the first headers or on the edge of the tablet. The final stage or follow up calculations for the Babylonian algorithm of summing base_60 reciprocals. This summing the shares was the proof that calculations were done correctly, but not included on some tablets.
A market rate procedure in TCL for just one unit price and available silver could be derived, which would be a simple problem, but shows the genesis of the Babylonian algorithm of summing base_60 reciprocals in using a false share. The Babylonians did not use algebra, but the explanation uses algebra for the context of developing a TCL procedure. The initial equation for one unit price would be $false_share * $unit_price = $available_silver. The $false_share equals $available_silver / $unit_price. The $false_share equals proc false_share1 { available_silver unit_price } { return < expr { $available_silver / $unit_price > }. There should be instances of either where the $available_silver equals one or where the $available_silver is greater than one. This is where the testcases come in to check the math. Now suppose that Babylonian mathematician wants to use two or multiple unit prices, say four unit prices. The initial equation for four unit prices would be $available_silver = $false_share * $unit_price_1 + $false_share * $unit_price_2 + $false_share * $unit_price_3 + $false_share * $unit_price_4. Combining the 4 unit prices and transposing, the $false_share = $available_silver / ( $unit_price_1 + $unit_price_2 + $unit_price_3 + $unit_price_4 ). Doable, but one is adding four new variables to the TCL procedure. The $false_share equals proc false_share2 { available_silver $unit_price_1 $unit_price_2 $unit_price_3 $unit_price_4 } { return < expr { $available_silver / ($unit_price_1 + $unit_price_2 + $unit_price_3 + $unit_price_4 ) > }. Now the Babylonian market did not use unit prices usually, but reported market rates only, so add an initial conversion step to transform market rates to market prices. In sexagesimal notation, a market price is the Base_60 reciprocal or inverse as expr < 60. / market_rate> and the Babylonian mathematicians used a tablet of reciprocal conversions. The Base_60 reciprocals are a little tricky that I admit, but we could put the reciprocal conversion scheme from market rates to market prices ahead of the proc false_share2. Once the value of the false share is found, the equation for programming the check answer is $available_silver = ( $false_share*$unit_price_1 + $false_share*$unit_price_2 + $false_share*$unit_price_3 + $false_share*$unit_price_4 ).
;# Babylonian algorithm of summing base_60 reciprocals
;# in using a false share
set unit_price_1 [ expr { 60. / $market_rate_1 } ]
set unit_price_2 [ expr { 60. / $market_rate_2 } ]
set unit_price_3 [ expr { 60. / $market_rate_3 } ]
set unit_price_4 [ expr { 60. / $market_rate_4 } ]
proc false_share2 { available_silver $unit_price_1 $unit_price_2 $unit_price_3 $unit_price_4 } { return [ expr { $available_silver / ($unit_price_1 + $unit_price_2 + $unit_price_3 + $unit_price_4 ) ] }| Table 10 for problem MS2299 | MS2299 was used as model problem in Friberg commentary | printed in | tcl wiki format | ||
|---|---|---|---|---|---|
| *** setup or initial stage for Babylonian algorithm of summing base_60 reciprocals *** | |||||
| given, available silver | 16_53_20 sexagesimal | ||||
| given, 4 unit costs | |||||
| *** midstage or follow up calculations, sum unit costs | |||||
| quantity | value | 60 / value | comment, if any | ||
| conventional id | reconstructed tablet value | base_60 reciprocal | |||
| market rate 1 | 3.0 | 20.0 | 5_55_33_20 | 17_46_40 | |
| market rate 2 | 4.0 | 15.0 | 4_26_40 | 17_46_40 | |
| market rate 3 | 5.0 | 12.0 | 3_33_20 | 17_46_40 | |
| market rate 4 | 6.0 | (10) | 2_57_46_40 | 17_46_40 | omitted on tablet |
| *** final stage , sum shares *** | |||||
| sum costs | 57.0 | expr {20.0+15.0+12.0 +10.0 } | cost relative numbers added correctly, but tricky in programming | ||
| given, available silver | 16_53_20 sexagesimal | available silver = expr {(16+(53./60)+(20./3600)) },16.8888 decimal Base_10 | |||
| scale factor | 17.7777 decimal | scale factor = expr {(16+(53./60)+(20./3600)) /(57/60.)}, 17.7777 decimal Base_10 | |||
| share a | 5.9259 | share a = expr { (20.0/60)* (16+(53./60)+(20./3600)) /(57/60.) }5.9259, decimal Base_10 | |||
| share b | 4.444425 | share b = expr { (15.0/60)* 17.7777 }4.444425 decimal Base_10 | |||
| share c | 3.55554 | share c = expr { (12.0/60)* 17.7777 }3.55554 decimal Base_10 | |||
| share d | 2.96294 | share d = expr { (10.0/60)* 17.7777 }2.962949 decimal Base_10 | |||
| sum shares | 16.88883 | equal to given, available silver | sum shares = expr { 5.92592 + 4.444425 + 3.55554 + 2.962949 }, 16.88883 | ||
| Note | ref Friberg commentary on tablet IM31210P4, | A Remarkable Collection of Babylonian Mathematical Texts. | |||
| Note | The tablets use Base_60 fractions | But the TCL calculations throw out modern Base_10 decimals |
| Table 9 for problem IM31210P4 | printed in | tcl wiki format | ||
|---|---|---|---|---|
| quantity | market rate value | market price value (60 / value) | comment, if any | |
| conventional id | reconstructed? tablet value | base_60 reciprocal | ||
| market rate 1 | 30. | 2.0 | 4.5833 | ref B. relative value, this 2 = 2 *60 |
| market rate 2 | 2.0 | 0.5 | 4.5833 | |
| market rate 3 | 1.3333 | 0.75 | 4.5833 | |
| market rate 4 | 0.75 | 1.3333 | 4.5833 | |
| sum costs | 4.5833 | cost relative numbers added correctly, but tricky in programming | ||
| share a | 10 | share a = expr { 20. * 30/60.} = 10. | ||
| share b | 40 | share b = exp=r { 20. * 2.} = 40. | ||
| share c | 26+40/60. | share c = expr { 20. * (1+20/60.)} = 26.6666 | ||
| share d | 15 | share d = expr { 20. * 45/60.} = 15. | ||
| sum shares | 1_31_40 sexagesimal | sum shares = expr { 10+40+26+40./60+15} = 91.6666, ~ 1+31/60+40/3600 | ||
| Note | ref Friberg commentary on tablet IM31210P4, | A Remarkable Collection of Babylonian Mathematical Texts. | ||
| Note | The tablets use Base_60 fractions | But the TCL calculations throw out modern Base_10 decimals |
c**2= a**2 + b**2
c**2= a**2 + 1 normalized Babylonian triplet
a**2 = c**2 -1 normalized Babylonian triplet
some b and c are both primes.
some b and c are not both primes.
The reciprocal pair relationship.
(X+1/X)**2 - (X+1/X)**2 = 4 , divide equation by 4
normalized triplet, < (1/4)* ((X+1/X)**2 ) , 1 ,(1/4)* ((X+1/X)**2) >
0 < X-1/X < 2
1< X-1/X < 1+sqrt(2) ~~ approximate limit of 2.4 Table 4. Reconstructed listing of Babylonian Base_60 inverse reciprocals
| Table 8 for Base_60 inverse reciprocals | printed in | tcl wiki format | ||
|---|---|---|---|---|
| Base_60 value | Base_60 inverse reciprocals or 60 / value | Base_10 value | Base_10 value of Base_60 inverse reciprocals | comment, if any |
| tablet value | base_60 reciprocal | |||
| 2 | 30 | 2 | 30 | |
| 3 | 20 | 3 | 20 | |
| 4 | 15 | 4 | 15 | |
| 5 | 12 | 5 | 12 | |
| 6 | 10 | 6 | 10 | |
| 8 | 7 30 | 8 | 7.5 | |
| 9 | 6 40 | 9 | 6.6666 | |
| 10 | 6 | 10 | 6 | |
| 12 | 5 | 12 | 5 | |
| 15 | 4 | 15 | 4 | |
| 16 | 3 45 | 16 | 3.75 | tablets for first ten powers of 3:45, interest rates??? |
| 18 | 3 20 | 18 | 3.3333 | |
| 20 | 3 | 20 | 3 | |
| 24 | 2 30 | 24 | 2.5 | |
| 25 | 2 24 | 25 | 2.4 | |
| 27 | 2 13 20 | 27 | 2.2222 | |
| 30 | 2 | 30 | 2 | |
| 32 | 1 52 30 | 32 | 1.875 | |
| 36 | 1 40 | 36 | 1.6666 | tablets for first ten powers of 1:40, interest rates??? |
| 40 | 1 30 | 40 | 1.5 | |
| 45 | 1 20 | 45 | 1.3333 | possible dealing with grain interest rate??? |
| 48 | 1 15 | 48 | 1.25 | |
| 50 | 1 12 | 50 | 1.2 | possible dealing with silver interest rate??? |
| 54 | 1 06 40 | 54 | 1.1111 | |
| 1 | 1 | 1 | 1 | exception handling alert 1=1 NE ( 60/value ) |
| 1 04 | 56 15 | 1.06666 | 56.250 | |
| 1 12 | 50 | 1.2 | 50 | superfluous, often omitted, possible dealing with silver interest rate??? |
| 1 15 | 48 | 1.25 | 48 | superfluous, often omitted |
| 1 20 | 45 | 1.33333 | 45.000 | superfluous, often omitted, possible dealing with grain interest rate??? |
| 1 21 | 44 26 40 | 1.35 | 44.4444 | |
| Note: | Babylonian mathematicians did >> not! << | usually use zeros | but in few instances | |
| Note: | Babylonian mathematicians separated Base_60 powers by spaces or gaps. | Moderns sometimes use periods (.) |
Flexible Push Button Operation in TCL calculator
gold 10/7/2018. Technical note on TCL calculator buttons addressing the reference ASK12 of 2017-02-19 . Many complex math programs have either initialize, refresh, or reset routines to force correct behavior, using calculator buttons. Of course, a very good feature of TCL is that new variables as number types do not have to be initialized prior to use. Repeating, setting a new number variable to 0 or 1 is not necessary prior to using the variable. I confess that habits brought from prior learned languages and 40 years ago are hard to change. Most of my gui programs on this wiki have a flexible button procedure (on changing labels and resetting variables prior to calculations). Where the program defaults are recalled, canvas colors/features/variables/clear displays are reset prior to ( in push button list) calculation. The buttons on the calculator are not limited to a single action proc or single shot. A button command may call multiple statements and procs like ::ttk::button .test4 -text "Test_wild_case3" -command {clearx; refresh_canvas_x .cv; fillup 120. 12.0 15.0 1. 1. 1. 1. 104.0; set global_variable 9999.;solve_routine;printout_routine;# need semicolons here; exit}. This is effectively a separate program or subprogram installed as list of procedures in a button. The TCL language is very flexible, and as experiments, the button may invoke a do while routine to call the listed button procs multiple times like the infinite repeater (SiFi). The button may invoke command and call procedures for a random number of times and random solutions, like nerve and muscle firings from the human brain in thought and speech (not SiFi). For cosmetics, the button may set colors, frame width, canvas objects, and variables with the random proc lpick from RS on the wiki. As long as duplicate frames, duplicate canvas, pack managers, and channels are not confused reference the original program, one can load secondary and entire procs into the button list. Returning to the conventional use of resetting variables, the button refresh and initialize tactic should work across the TCL versions, at least in the versions tested (TCL8.5, and TCL8.6).
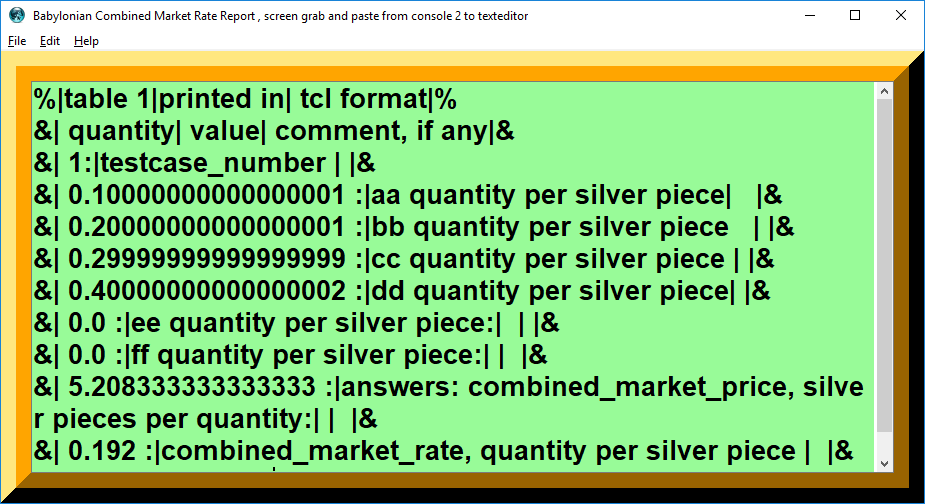
Most of the testcases involve experiments or models, using assumptions, and rules of thumb. For the push buttons in the TCL calculator, the recommended procedure is push testcase and fill frame, change first three entries etc, push solve, and then push report. Report allows copy and paste from console to conventional texteditor. For testcases in a computer session, the TCL calculator increments a new testcase number internally, eg. TC(1), TC(2) , TC(3) , TC(N). The testcase number is internal to the calculator and will not be printed until the report button is pushed for the current result numbers. The current result numbers should be cleared either on the clear button or on the next solve button.
Testcases Section
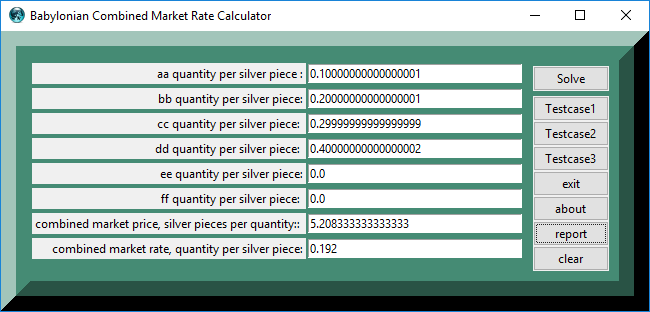
Testcase 1
| positive Numbers | ||
|---|---|---|
| table 1 | printed in | tcl format |
| quantity | value | comment, if any |
| 1: | testcase_number | |
| 0.1 : | aa quantity per silver piece | |
| 0.2 : | bb quantity per silver piece | |
| 0.3 : | cc quantity per silver piece | |
| 0.4 : | dd quantity per silver piece | |
| 0.0 : | ee quantity per silver piece: | |
| 0.0 : | ff quantity per silver piece: | |
| 5.2083 : | answers: combined_market_price, silver pieces per quantity: | |
| 0.192 : | combined_market_rate, quantity per silver piece |
Testcase 2
| Mixed positive & negative N. | ||
|---|---|---|
| table 2 | printed in | tcl format |
| quantity | value | comment, if any |
| 2: | testcase_number | |
| -0.1 : | aa quantity per silver piece | |
| -0.2 : | bb quantity per silver piece | |
| 0.3 : | cc quantity per silver piece | |
| 0.4 : | dd quantity per silver piece | |
| 0.0 : | ee quantity per silver piece: | |
| 0.0 : | ff quantity per silver piece: | |
| -2.2916 : | answers: combined_market_price, silver pieces per quantity: | |
| -0.4363 : | combined_market_rate, quantity per silver piece |
---
Testcase 3
| mixed zeros and Numbers | ||
|---|---|---|
| original CMR formula balks on unexpected zero's, div by zero | ||
| table 3 | printed in | tcl format |
| quantity | value | comment, if any |
| 3: | testcase_number | |
| 0.1 : | aa quantity per silver piece | |
| 0.0 : | bb quantity per silver piece | |
| 0.0 : | cc quantity per silver piece | |
| 0.2 : | dd quantity per silver piece | |
| 0.3 : | ee quantity per silver piece: | |
| 0.4 : | ff quantity per silver piece: | |
| 5.2083 : | answers: combined_market_price, silver pieces per quantity: | |
| 0.192 : | combined_market_rate, quantity per silver piece |
Testcase 4a
| price data from grocery pump | ||
|---|---|---|
| from prices on pump | printed in | tcl wiki format |
| 1 / (fuel price) | fuel price | comment, if any |
| market rate | dollars per gallon | |
| 0.5524 | 1.81 | regular gas |
| 0.4807 | 2.08 | midgrade gas |
| 0.42918 | 2.33 | premium gas |
| 0.47846 | 2.09 | diesel fuel |
| Note. Dollar was originally a silver piece of one ounce |
Testcase 4b
| fuel pump market rates in calculator | ||
|---|---|---|
| Original units, dollars per gallon & gallons per dollars | ||
| table 4b | printed in | tcl format |
| quantity | value | comment, if any |
| 4b: | testcase_number | |
| 0.5524 : | aa quantity per silver piece | |
| 0.4807 : | bb quantity per silver piece | |
| 0.4292 : | cc quantity per silver piece | |
| 0.4746 : | dd quantity per silver piece | |
| 0.0 : | ee quantity per silver piece: | |
| 0.0 : | ff quantity per silver piece: | |
| 2.0818 : | answers: combined_market_price, silver pieces per quantity: | |
| 0.4803 : | combined_market_rate, quantity per silver piece |
Testcase 5, heavily modified script, fine and common oil & MS3895 midstages
| table 5 | printed in | tcl format |
|---|---|---|
| quantity | value | comment, if any |
| 5: | testcase_number | |
| 3.0 : | market rate 1, quantity per silver piece: | |
| 12.0 : | market rate 2, quantity per silver piece: | |
| 1.0 : | total market price, usually silver pieces: | |
| 0.80 : | answers, market price 1, usually silver pieces: | 48/60 gin in base 60 fraction |
| 0.20 : | market price 2, usually silver pieces: | 12/60 gin in base 60 fraction |
| 1.0 : | total market price 1&2, check, usually silver pieces: | calculated check on solution |
| 36.0 : | rectangle_area: | |
| 7.5 : | half_sum: | |
| 4.5 : | half_diff: | |
| 20.25 : | square_half_diff: | |
| 0.2083 : | combined_market_price, silver pieces per quantity: | |
| 4.8 : | combined_market_rate, quantity per silver piece |
Testcase 6, silver= 1 (60 parts)
| table 6 | printed in | tcl format |
|---|---|---|
| quantity | value | comment, if any |
| 2: | testcase_number | MS2299,modified proc |
| 3.0 : | aa quantity per silver piece | |
| 4.0 : | bb quantity per silver piece | |
| 5.0 : | cc quantity per silver piece | |
| 6.0 : | dd quantity per silver piece | |
| 0.0 : | ee quantity per silver piece: | |
| 0.0 : | ff quantity per silver piece: | |
| check answer = 60.000 : | answers: sum of base_60 shares, check answer, usually 60: | |
| 21.053 15.789 12.632 10.526 : | base_60 shares , fraction silver piece per share: |
Testcase 7, silver= 1 (60 parts)
| table 7 | printed in | tcl format |
|---|---|---|
| quantity | value | comment, if any |
| 1: | testcase_number | MS2832,MS2830rev, modified proc , Friberg |
| 1.0 : | aa quantity per silver piece | |
| 2.0 : | bb quantity per silver piece | |
| 3.0 : | cc quantity per silver piece | |
| 4.0 : | dd quantity per silver piece | |
| 0.0 : | ee quantity per silver piece: | |
| 0.0 : | ff quantity per silver piece: | |
| check answer = 60.000 : | answers: sum of base_60 shares, check answer, usually 60: | |
| 28.800 14.400 9.6000 7.2000 : | base_60 shares , fraction silver piece per share: |
Testcase 8, silver= 1 (60 parts)
| table 8 | printed in | tcl format |
|---|---|---|
| quantity | value | comment, if any |
| 8: | testcase_number | MS2830rev,Friberg, modified proc |
| 2.0 : | aa quantity per silver piece | |
| 3.0 : | bb quantity per silver piece | |
| 15.0 : | cc quantity per silver piece | |
| 6.0 : | dd quantity per silver piece | |
| 0.0 : | ee quantity per silver piece: | |
| 0.0 : | ff quantity per silver piece: | |
| check answer = 60.000 : | answers: sum of base_60 shares, check answer, usually 60: | |
| 28.125 18.750 3.7500 9.3750 : | base_60 shares , fraction silver piece per share: |
Testcase 9, silver= 1 (60 parts)
| table 9 | printed in | tcl format |
|---|---|---|
| quantity | value | comment, if any |
| 5: | testcase_number | MS 2268/19, obv,Friberg, modified proc |
| 3.5 : | aa quantity per silver piece | fraction from 3+30/60 |
| 5.833 : | bb quantity per silver piece | fraction from 5+50/60 |
| 7.0 : | cc quantity per silver piece | |
| 7.5 : | dd quantity per silver piece | fraction from 7+30/60 |
| 14.0 : | ee quantity per silver piece: | |
| 0.0 : | ff quantity per silver piece: | |
| check answer = 60.000 : | answers: sum of base_60 shares, check answer, usually 60: | |
| 21.302 12.781 10.651 9.9408 5.3254 : | base_60 shares , fraction silver piece per share: |
Testcase 10, problem MS3895 ref Friberg.
| MS3895 initial entries are overspecified here | ||
|---|---|---|
| table 10 | printed in | tcl format |
| quantity | value | comment, if any |
| 10: | testcase_number | |
| 90 : | capacity in oil silas: | decimal for 1_30 base_60, given |
| 6 : | profit in silver pieces: | given |
| 0.75 decimal : | mr1-mr2, sila per sheka: | given as 45/60 base_60 |
| **** not given follows below **** | ||
| 3.75 decimal: | market rate 1, quantity per silver piece: | decimal for 3_45 base_60, not given follows |
| 3.0 : | market rate 2, quantity per silver piece: | not given |
| 24.0 : | total market price, usually silver pieces: | expr 90*(1/3.75)= 24.0 |
| 24. : | market price 1, usually silver pieces: | expr 90*(1/3.75)= 24.0 |
| 30. : | market price 2, usually silver pieces: | expr 90*(1/3.0)= 30.0 |
| 6.0 : | total profit, check, usually silver pieces: | expr 30-24 |
| 11.25 : | rectangle_area: | expr (3.)*(90./24) |
| 3.375 : | half_sum: | expr .5*(3.75+3) |
| 0.375 : | half_diff: | expr .5*(3.75-3) |
| 0.140625 : | square_half_diff: | expr (.5*(3.75-3))**2 |
| 1.666 : | combined_market_rate, quantity per silver piece |
Screenshots Section
figure 1.
References:
- Wikipedia search engine < Harmonic mean >
- Wikipedia search engine < average mean >
- Wikipedia search engine < Babylonian Math >
- Google search engine < Harmonic_mean >
- Book >> ref Joran Friberg commentary on YBC4698 , A Remarkable Collection of Babylonian Mathematical Texts.
- Harmonic Mean By Adam Hayes
- en.wikipedia.org/wiki/Harmonic_mean
- Math proc Template called ::math::quantity_into_ratios, reference
- Math proc templates for Prime Number generation and TCL demo example, numerical analysis
- www.gigacalculator.com/calculators/harmonic-mean-calculator
- Mathematical Treasure: Old Babylonian Area Calculation, uses ancient method
- Frank J. Swetz , Pennsylvania State University
- Wikipedia, see temple of Edfu, area method used as late as 200 BC in Egypt.
- Oneliner's Pie in the Sky
- One Liners
- Category Algorithm
- Brahmagupta Area of Cyclic Quadrilateral and eTCL demo example calculator
- Gauss Approximate Number of Primes and eTCL demo example calculator
- goggle "Babylonian Number cuneiform Series"
- Oneliner's Pie in the Sky
- One Liners
- google < Babylonian Interest Rates Wikipedia >
- Ancient Babylonian Algorithms, Donald E. Knuth, Stanford University
- The oldest example of compound interest in Sumer, seventh power of four thirds (4/3)**7 , Kazuo MUROI
- Interest, Price, and Profit: An Overview of Mathematical Economics in YBC 46981,
- Robert Middeke-Conlin Christine Proust, CNRS and Université Paris Diderot
- Compound Interest Doubling Time Rule: Extensions and Examples from Antiquities,
- Saad Taha Bakir, ISSN: 2241 - 1968 (print), 2241 – 195X (online)
- Two Sumerian Words of Fractions in Babylonian Mathematics: igi-n-gál and igi-te-en , Kazuo MUROI
- O. Neugebauer and A. Sachs, Mathematical Cuneiform Texts, American Oriental Society, Series 29. New Haven, 1945.
- K. Muroi, Interest Calculation in Babylonian Mathematics:
- New Interpretations of VAT 8521 and VAT 8528, Historia Scientiarum, 39, (1990), 29-34
- O. Nuegebauer, The Exact Sciences in Antiquity, Second edition, Dover Publication Inc., New York, 1969
- Square Root , Keith Vetter
- A little slide-rule
- What if you do not have exp()?
- Category Algorithm
- A Remarkable Collection of Babylonian Mathematical Texts, Joran Friberg, 2007
- Chalmers University of Technology Gothenburg, Sweden
- Weighted means and means as weighted sums
- Morningstar Methodology Paper, Average Price Ratios
- Joran Friberg and andrew george,
- Six more mathematical cuneiform texts in the Schoyen collection, MS 3895,
- A market rate problem (fine oil). Includes refs to YBC 4698, MLC 1842,
- TMS 13, and IM 54464, parallel texts to MS 3895.
- Interest, Price, and Profit: An Overview of
- Mathematical Economics in YBC 46981,
- Robert Middeke-Conlin & Christine Proust,
- CNRS and Universite Paris Diderot
- Amazing Traces of a Babylonian Origin in Greek Mathematics,
- Joran Friberg
- A Remarkable Collection of Babylonian Mathematical Texts:
- Manuscripts in the Schøyen Collection: Cuneiform Texts I},
- Joran Friberg
- Basic Mathematics for Electricity and Electronics,
- Bertrand Singer
- Basic Mathematics for Electronics,
- Cooke,Adams, and Dell
- Babylonian Mathematical Astronomy: Procedure Texts
- - Mathieu Ossendrijver, trapezoids in astronomy
- measures Jupiter motion
Pseudocode & Equations Section
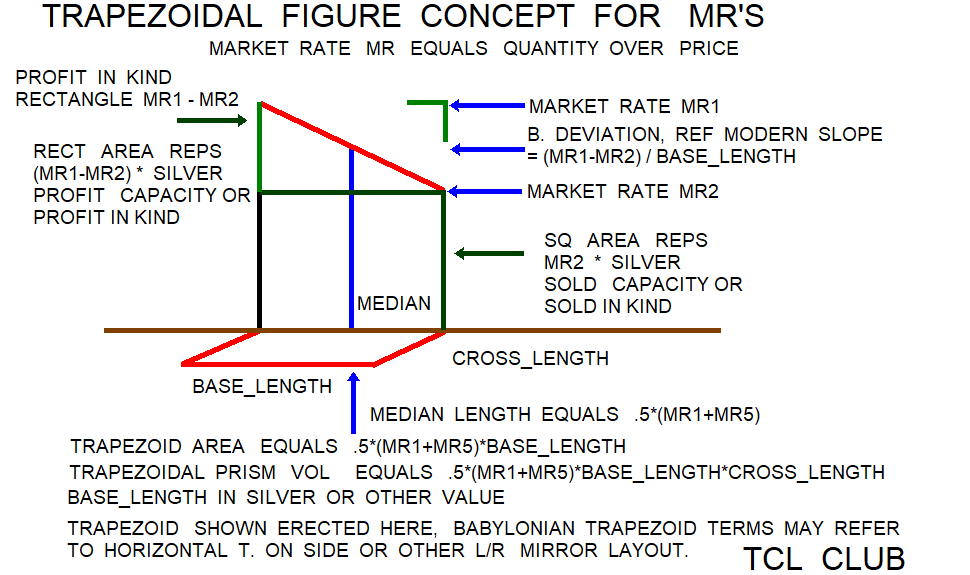
Western trapezoid formulas
and trapezoidal prism volume
following includes algebraic expressions,
terms, and notation not used on tablets
side_aa refs top, t. on side
side_bb refs bottom, t. on side
side_cc refs height, t. on side
median_length = .5*(side_aa+side_bb)
trapezoid_area= 0.5*(side_aa+side_bb)*height
trapezoid_area= median*height
trapezoidal_prism_volume=
t. vol=length*(0.5*(side_aa+side_bb))*height
median divides equal side lengths
Babylon market rate problems
set up math expressions
slant_deviation=(side_aa-side_bb)/height
possibly set side_aa >? side_bb in Babylon???
generic linear solution for 2 market_rates
1) Price_P1 equals (1 / market_rate_1)
2) Price_P2 equals (1 / market_rate_2),
divide equations 1) and 2)
3) P1 = (market_rate_2 / market_rate_1) * P2
4) P2= (market_rate_1 / market_rate_2)*P1
5) P1+P2=1 , set from problem in this case
6) P1 = 1-P2 or
7) P2 = 1-P1
equivalent math expressions from mr tablets
average of two rates or t. median
.5*(mr1+mr2)
half the difference of two rates
.5*(mr1-m2)
possible trapezoid slant_deviation
height?*(mr1-m2), mr1 >? mr2
square of half the difference of two rates
(.5*(mr1-m2))**2
product of two rates, treated as area?
mr1*mr2
dollar was originally a silver piece of one ounceAppendix Code
appendix TCL programs and scripts
# pretty print from autoindent and ased editor
# Babylonian Combined Market Rate V5
# written on Windows XP on TCL
# working under TCL version 8.6
# gold on TCL Club, 4oct2018
package require Tk
package require math::numtheory
namespace path {::tcl::mathop ::tcl::mathfunc math::numtheory }
set tcl_precision 17
frame .frame -relief flat -bg aquamarine4
pack .frame -side top -fill y -anchor center
set names {{} {capacity, quantity usually silas:} }
lappend names {market rates mr1-mr2, diff quantity usually silas per silver piece:}
lappend names {total profit, usually silver pieces:: }
lappend names {answers, market price 1, usually silver pieces: }
lappend names {market price 2, usually silver pieces:}
lappend names {total market price 1&2, check, usually silver pieces: }
lappend names {combined market price, silver pieces per quantity:: }
lappend names {combined market rate, quantity per silver piece:}
foreach i {1 2 3 4 5 6 7 8} {
label .frame.label$i -text [lindex $names $i] -anchor e
entry .frame.entry$i -width 35 -textvariable side$i
grid .frame.label$i .frame.entry$i -sticky ew -pady 2 -padx 1 }
proc about {} {
set msg "Calculator for Babylonian Combined Market Rate V5
from TCL ,
# gold on TCL Club, 10aug2018 "
tk_messageBox -title "About" -message $msg }
proc self_help {} {
set msg "Calculator for Babylonian Combined Market Rate V5
from TCL ,
# self help listing
# 2 market_rates require solution of 2 linear equations,
# whether problem is ancient B. or modern. 3 givens follows.
1) capacity, quantity usually silas
2) market rates mr1-mr2,
diff quantity usually silas per silver piece
3) total profit, usually silver pieces
The Babylonians did not use modern algebraic notation.
The linear equation(s) solution from the clay tablets
is genuine antique algorithm from 1600 BCE
and different looking from modern math methods.
The proc market_solution is adapted from the
clay tablet MS3895 etc translated and explained by Friberg.
The proc ::math::combined_market_rate was
adapted from tcl Stats 2011-05-22, arithmetic mean <RLE>
The proc ::math::combined_market_rate was written
compatible with TCLLIB.
1) Price_P1 equals (1 / market_rate_1)
2) Price_P2 equals (1 / market_rate_2)
3) P1 = (market_rate_2 / market_rate_1) * P2
4) P2= (market_rate_1 / market_rate_2)*P1
5) P1+P2 = 1 , for simple cases only, total price = 1
6) P1 = 1-P2 , for simple cases only, total price = 1
7) P2 = 1-P1 , for simple cases only, total price = 1
# cuneiform market rate derives from trade in kind
# includes capacity in jars of fine oil and bushels of barley.
# market rate defined as quantity per price
# or 1 over (price per quantity)
# market price defined as price per quantity
# or 1 over ( quantity per price)
# However, there was lack of small currency in
# Ancient Mesopotamia and most transactions were in kind.
# Market rates were more conveniant in trade and accounting.
# Recommended procedure is push testcase and fill frame,
# change first three entries etc, push solve,
# and then push report. Report allows copy and paste
# from console to conventional texteditor. For testcases
# testcase number is internal to the calculator and
# will not be printed until the report button is pushed
# for the current result numbers.
# This posting, screenshots, and TCL source code is
# copyrighted under the TCL/TK 8.6 license terms.
# Editorial rights retained under the TCL/TK license terms
# and will be defended as necessary in court.
Conventional text editor formulas or grabbed from internet
screens can be pasted into green console.
Try copy and paste following into green screen console
::math::combined_market_rate 1 2 3 4 , answer 1.92
::math::combined_market_rate 0.5524 0.4807 0.42918 0.47846
answer = 0.48131
market_solution 90.0 0.75 6.
answer list = < 90 0.75 6. 3.354 9.375 8.625 9 1>
market_solution 770. 4.0 40.0
answer list = <770. 4.0 40.0 8.774 11.0 7.0 9 1>
set answer [* 1. 2. 3. 4. 5. ]
returns 120
# gold on TCL Club, 10aug2018 "
tk_messageBox -title "About" -message $msg }
# adapted from tcl Stats 2011-05-22, arithmetic mean <RLE>
# ::math::combined_market_rate --
#
# Return the combined_market_rate by one,two, or more given rates
# market rate defined as quantity per price
# or 1 over (price per quantity)
#
# Arguments:
#
# args values are one, two, or more given rates
#
# Results: combined_market_rate
# works for positive numbers, negative numbers,
# and mixed positive & negative numbers.
# arg of zero returns zero
# arg of null returns zero
# filter foreach drops irregular zero elements from argument
proc ::math::combined_market_rate { args} {
set sum 0.
set N [ expr { [ llength $args ] } ]
if { $N == 0 } { return 0 }
if { $N == 1 || [ lindex $args 0 ] == 0 } { return 0 }
set res {};set counter2 0;
# filter foreach drops irregular zero elements
foreach item $args {if {$item != 0 } {incr counter2 1; lappend res $item } }
set counter 0
foreach val $res {
set sum [ expr { $sum + 1./$val } ]
incr counter 1
}
set combined_market_rate1 [ expr { 1./(($sum*1.)/$counter2) } ]
return $combined_market_rate1
}
# various testcases on combined_market_rate
# puts [::math::combined_market_rate 0.5524 0.4807 0.42918 0.47846 ]
# answer 0.48131 "
# puts [ ::math::combined_market_rate .1 .2 .3 .4 ]
# answer 0.192
# ::math::combined_market_rate -.1 -.2 -.3 -.4
# answer -0.192, correct
# operator math formula follows
# check [/ 1. [/ [+ [/ 1. -.1] [/ 1. -.2] [/ 1. -0.3 ] [/ 1. -0.4] ] 4. ] ]
# returns -0.192, correct
# puts " [ ::math::combined_market_rate .1 ] "
# :math::combined_market_rate -.1 -.2 .3 .4
# answer -0.4363636363636364
# operator math formula follows
# set check [/ 1. [/ [+ [/ 1. -.1] [/ 1. -.2] [/ 1. 0.3 ] [/ 1. 0.4] ] 4. ] ]
# check equals -0.4363636363636364
# puts " for (::math::combined_market_rates .1)
# returns .1 "
# ::math::combined_market_rate {}
# null returns zero, correct.
# ::math::combined_market_rate 0
# arg 0 returns zero, correct.
# addition dated 24sep2018
# added filter foreach to remove zero's
# irregular zeros,
# test on zero's 0.1 0.0 0.0 0.2 0.3 0.4
# returns 0.192 , correct
# test on zero's 0.1 0.0 0.0 0.2 0.3 0.4
# returns 0.192 , correct
proc market_solution { capacity1 mr1_minus_mr2 total_profit2} {
global side1 side2 side3 side4 side5
global side6 side7 side8
global rectangle_area half_sum half_diff
global square_half_diff market_silver1 market_silver2
global market_silver_total
global mr1_star_mr2 market_rate1 market_rate2 mr1_plus_mr2_div2
set sum 0.
set mr1_star_mr2 1
set mr1_star_mr2 [ expr { (1./$total_profit2)*$capacity1*$mr1_minus_mr2 } ]
set mr1_star_mr2 [ expr { 1./$total_profit2*$capacity1*$mr1_minus_mr2 } ]
set mr1_plus_mr2_div2 [ expr { sqrt( $mr1_minus_mr2+$mr1_star_mr2 ) } ]
set market_rate1 [ expr { $mr1_plus_mr2_div2 + (.5*$mr1_minus_mr2) } ]
set market_rate2 [ expr { $mr1_plus_mr2_div2 - (.5*$mr1_minus_mr2) } ]
set market_silver1 [ expr { 1. / ($market_rate1 / $market_rate2 + 1.) } ]
set market_silver2 [ expr { 1. / ($market_rate2 / $market_rate1 + 1.) } ]
set market_silver_total [+ $market_silver1 $market_silver2 ]
set rectangle_area [* $market_rate1 $market_rate2 ]
set half_sum [/ [+ $market_rate1 $market_rate2 ] 2. ]
set half_diff [/ [- $market_rate1 $market_rate2 ] 2. ]
set square_half_diff [** [/ [- $market_rate1 $market_rate2 ] 2. ] 2]
set answer 1
return $answer
}
proc calculate { } {
global answer2
global side1 side2 side3 side4 side5
global side6 side7 side8
global testcase_number
global rectangle_area half_sum half_diff
global square_half_diff market_silver1 market_silver2
global market_silver_total
global mr1_star_mr2 market_rate1 market_rate2 mr1_plus_mr_div2
incr testcase_number
set side1 [* $side1 1. ]
set side2 [* $side2 1. ]
set side3 [* $side3 1. ]
set side4 [* $side4 1. ]
set side5 [* $side5 1. ]
set side6 [* $side6 1. ]
set side7 [* $side7 1. ]
set side8 [* $side8 1. ]
set capacity2 $side1
set lister { $side1 $side2 $side3 $side4 $side5 $side6 }
set market_solution5 1
set market_solution5 [ market_solution $side1 $side2 $side3 ]
set combined_market_rate5 1.
set combined_market_rate5 [ ::math::combined_market_rate $market_rate1 $market_rate2]
set combined_market_price5 [/ 1. $combined_market_rate5 ]
set market_silver1 [/ $capacity2 $market_rate1 ]
set market_silver2 [/ $capacity2 $market_rate2 ]
set market_silver_total [+ $market_silver1 $market_silver2 ]
set side4 $market_silver1
set side5 $market_silver2
set side6 $market_silver_total
set side7 $combined_market_price5
set side8 $combined_market_rate5
}
proc fillup {aa bb cc dd ee ff gg hh} {
.frame.entry1 insert 0 "$aa"
.frame.entry2 insert 0 "$bb"
.frame.entry3 insert 0 "$cc"
.frame.entry4 insert 0 "$dd"
.frame.entry5 insert 0 "$ee"
.frame.entry6 insert 0 "$ff"
.frame.entry7 insert 0 "$gg"
.frame.entry8 insert 0 "$hh"
}
proc clearx {} {
foreach i {1 2 3 4 5 6 7 8 } {
.frame.entry$i delete 0 end } }
proc reportx {} {
global side1 side2 side3 side4 side5
global side6 side7 side8
global testcase_number
global rectangle_area half_sum half_diff
global square_half_diff market_silver1 market_silver2
global market_silver_total
global mr1_star_mr2 market_rate1 market_rate2 mr1_plus_mr2_div2
console show;
console eval {.console config -bg palegreen}
console eval {.console config -font {fixed 20 bold}}
console eval {wm geometry . 40x20}
console eval {wm title . " Babylonian Combined Market Rate Report V5, screen grab and paste from console 2 to texteditor"}
console eval {. configure -background orange -highlightcolor brown -relief raised -border 30}
puts "%|table $testcase_number|printed in| tcl format|% "
puts "&| quantity| value| comment, if any|& "
puts "&| $testcase_number:|testcase_number | |&"
puts "&| $side1 :|capacity, quantity usually silas: | |&"
puts "&| $side2 :|market rates mr1-mr2, quantity usually silas per silver piece: | |& "
puts "&| $side3 :|total profit, usually silver pieces: | |& "
puts "&| $mr1_star_mr2 :| mr1_star_mr2, quantity usually sila: | |& "
puts "&| $mr1_plus_mr2_div2 :| mr1_plus_mr_div2, quantity usually sila: | |& "
puts "&| $market_rate1 :|market_rate1, quantity usually sila: | |& "
puts "&| $market_rate2 :|market_rate2, quantity usually sila: | |& "
puts "&| $market_silver1 :|market price 1, usually silver pieces:| |&"
puts "&| $market_silver2 :|market price 2, usually silver pieces:| | |&"
puts "&| $market_silver_total :|total market price 1&2, check, usually silver pieces:| | |&"
puts "&| $rectangle_area :|rectangle_area:| | |&"
puts "&| $half_sum :|half_sum:| | |&"
puts "&| $half_diff :|half_diff:| | |&"
puts "&| $square_half_diff :|square_half_diff:| | |&"
puts "&| $side4 :|answers, market price 1, usually silver pieces:| | |&"
puts "&| $side5 :|market price 2, usually silver pieces:| | |&"
puts "&| $side6 :|total market price 1&2, check, usually silver pieces:| | |&"
puts "&| $side7 :|combined_market_price, silver pieces per quantity:| | |&"
puts "&| $side8 :|combined_market_rate, quantity per silver piece | |&"
}
frame .buttons -bg aquamarine4
::ttk::button .calculator -text "Solve" -command { calculate }
::ttk::button .test2 -text "Testcase1" -command {clearx;fillup 770. 4.0 40.0 70. 110. 180. 0.117 8.55}
::ttk::button .test3 -text "Testcase2" -command {clearx;fillup 90.0 0.75 6. 23.4 29.1 52.5 0.29 3.42 }
::ttk::button .test4 -text "Testcase3" -command {clearx;fillup 300.0 2. 7.5 29.8 37.3 67.2 0.11 8.9 }
::ttk::button .clearallx -text clear -command {clearx }
::ttk::button .about -text about -command {about}
::ttk::button .self_help -text self_help -command {self_help}
::ttk::button .console2 -text report -command { reportx }
::ttk::button .exit -text exit -command {exit}
pack .calculator -in .buttons -side top -padx 10 -pady 5
pack .clearallx .console2 .self_help .about .exit .test4 .test3 .test2 -side bottom -in .buttons
grid .frame .buttons -sticky ns -pady {0 10}
. configure -background aquamarine4 -highlightcolor brown -relief raised -border 30
wm title . "Babylonian Combined Market Rate Calculator V5"
# gold on TCL Club, 4oct2018
# This posting, screenshots, and TCL source code is
# copyrighted under the TCL/TK 8.6 license terms.
# Editorial rights retained under the TCL/TK license terms
# and will be defended as necessary in court.
# end of fileAppendix procs for testcases
# These formulas for parallel resistors
# can be pasted into
# the Easy Eye calculator console.
# Compact procs were used to check
# main calc proc and develop testcases.
# formula for two parallel resistors of
# resistance r1 and r2 ohms.
proc parallel_resistor2 {r1 r2 } { return [ expr (($r1 * $r2 )/ ($r1+ $r2))]}
# usage: set resistor [ parresistor 100 100 ];answer is 50.
# formula for three parallel resistors
# of resistance r1, r2, and r3 ohms.
proc parallel_resistor3 {r1 r2 r3 } { return [ expr (($r1*$r2*$r3)/($r1*$r2+$r2*$r3+$r2*$r3))]}
# end of file Notes on charts, small case from graphics tags
Notes on charts.small case from graphics tags. trapezoidal figure concept for Babylonian market rates. market rate mr equals quantity over price. market price equals price over quantity. sq area reps mr2 * silver sold capacity or sold in kind. median length equals .5*(mr1+mr5) . trapezoid area equals .5*(mr1+mr5)*base_length . median length equals .5*(mr1+mr5). trapezoidal prism vol equals .5*(mr1+mr5)*base_length*cross_length . cross_length median base_length deviation = b. deviation, ref modern slope = (mr1-mr2) / base_length. trapezoid shown erected here, Babylonian trapezoid terms may refer to horizontal trapezoid on side or other l/r mirror layout. base_length in silver or other value. tcl club trapezoidal figure concept for mr's. rectangular area reps (mr1-mr2) * silver profit capacity or profit in kind. cuneiform market rate derives from trade in kind includes capacity in jars of fine oil and bushels of barley. market rate mr equals quantity over price cuneiform market rate derives from trade in kind. .base_length in silver or other value trapezoid shown erected here, Babylonian trapezoid terms may refer to horizontal t. on side or other l/r mirror layout. market rate mr2 median length equals .5*(mr1+mr5). Babylonian deviation, ref modern slope = (mr1-mr2) / base_length. median length equals .5*(mr1+mr5). trapezoid area equals .5*(mr1+mr5)*base_length. trapezoidal prism vol equals .5*(mr1+mr5)*base_length*cross_length. sq area reps mr2 * silver sold capacity or sold in kind. rectangular area reps (mr1-mr2) * silver profit capacity or profit in kind profit in kind. rectangle mr1 - mr2 market price equals price over quantity. market rate mr2 Babylonian deviation, ref modern slope = (mr1-mr2) / base_length. trapezoid area equals .5*(mr1+mr5)*base_length. trapezoidal prism vol equals .5*(mr1+mr5)*base_length*cross_length. median length equals .5*(mr1+mr5). sq area reps mr2 * silver sold capacity or sold in kind (mr1-mr2) * silver. profit capacity or profit in kind rectangular area reps (mr1-mr2) * silver profit capacity or profit in kind. cuneiform market rate derives from trade in kind includes capacity in jars of fine oil and bushels of barley.
Comments Section
Please place any comments here, Thanks.
aplsimple - 2018-10-08 05:26:38
Would you so kind to give the TCL Club link? {gold] https://www.facebook.com/groups/tcltk/ . You may be interested in file "Free TCL books and docs from Facebook TCL Club.odt" on club file system. However, I am not sure this file format is sufficiently clean and presentable to the wiki. PS. I can not access your moniker or bio page, has the wiki loaded such a page for you. This should be automatic and your filling out page is voluntary.