Boolean Logic
Theo Verelst 2003-04-16
Or: how to use the logical expr or condition clauses and functions made of procs for important and fundamental logical, two valued functions...
Boolean logic is the formal mathematical foundation of the most fundamental computer circuits, as well as a major component in the design of complex digital circuits, and as such is important for every serious programmer to at least have some knowledge about, unless one wants to be bereft of fundamental, relevant and fun concepts, and not be aware of the reason for the efficiency of certain and inefficiency of other programming constructs.
In Tcl, it is fun to interactively play around with these fundamentals, to begin with in basic form, later I'll do a page where these principles are applied and shown graphically.
As almost everybody (here) will know, booleans are two valued numbers, meaning they are 1 or 0, or in electronic circuits that carry them, a high or a low signal, for instance 5 Volts or 0 Volts. Like with decimal numbers, we can combine 1's and 0's in a list, like decimal numbers, and define operations on them. Parallel operations as with decimal numbers can be defined, which can like in the decimal case be carried out using distributive and associative and substituation operations and factoring.
The basic operations are invert, and and or, which can be defined in tcl as:
proc inv a {return [expr !$a]}
proc and {a b} {return [expr $a && $b]}
proc or {a b} {return [expr $a || $b]}We can list the domain and corresponding logical functions values easily in short lists:
# truth table format:
# inputs --> output
# msb lsb
for {set i 0} {$i < 2} {incr i} {puts "$i [inv $i]"}
0 1
1 0
for {set j 0} {$j < 2} {incr j} { for {set i 0} {$i < 2} {incr i} {puts "$j$i [and $j $i]"}}
00 0
01 0
10 0
11 1
for {set j 0} {$j < 2} {incr j} { for {set i 0} {$i < 2} {incr i} {puts "$j$i [or $j $i]"}}
00 0
01 1
10 1
11 1We can define a nand as the combination of an inverter and a AND circuit as a nand:
proc nand {a b} {return [inv [and $a $b]]}With as truth table:
for {set j 0} {$j < 2} {incr j} { for {set i 0} {$i < 2} {incr i} {puts "$j$i [nand $j $i]"}}
00 1
01 1
10 1
11 0Combining more than one bit in a conceptual 'word' we can distinguish the weight of the bits, and like with decimal numbers place the highest valued bit left, and the one valued bit at the right. Because every bit contributes a doubling of the set of possible numbers the word can take on, we can say the corresponding weight of each bit is pow(2,n), where n is the bit number starting from zero at the right. The highest number thus formed 11111...1 is pow(2,n)-1, taking the lowest to have corresponding decimal value zero, and represented as 0000...0.
A separate page of course could be about the conversions possible between numbers in various representations, here we take it that all we need to know is that numbers exist, and that pow(2,n) distinguishable numbers exist for a word of n bits.
Now an important logical circuit and theory concept is the combination of logical circuits, and possibilities to select and combine. We've seen the nand function as combination of and and invert, but we can also combine two variable / input functions. Before succumbing to wieldy and large ranges of possibilities that would come from all possible combinations of logical functions, we can stand on the shoulders of generations of digital designers, and limit ourselves to sets of functions and their combinations that can be proven to span the range of all possible digital function mappings of any number of input and output bits.
The main thought is that we can start with a select function, which is capable of transfering the logical value of one input to the output.
First we regard a logical function that is defined as one for exactly one input combination, such as for a and function, where we have only a 1 at the output when both inputs are 1. We can extend that to a and with more than two inputs:
and_ninputs = and_1(
i1, and_2(
i2, and_3(
i3,
....
and_n-1(in-1, in)
)
)
)Intuitively we can understand that the only way to make all ands give out a 1 is to feed all inputs with a 1, otherwise one or more will spoil the overall 1 for certain and 'gates'. Logical designers would never built this circuit with longest path of n-1, because that would have corresponding electronical signal delay, but built it like a tree, which is logically equivalent, as long as the truth table is 1 only and strictly for all inputs being set to 1.
Now for a set of digital values corresponding to the full set of possible numbers corresponding to n bits of information, we can define n functions such that for each combination there is exactly one function that evaluates to a 1, and all others zero. Assuming a andn function and a invert-or-not (let's call it exor) function that can take any number of inputs, such function set can be generated as follows:
select = andn( inv(exor (i1,select1)), inv(exor (i2,select2)), inv(exor (in,selectn)), ...) (non-tcl notation)
Where the select1 ... selectn bits are set to the value the function is supposed to return 1 for. The exor is exclusive or also called comparator, which has truth table:
in1 in2 exor not_exor -------------------------- 0 0 0 1 0 1 1 0 1 0 1 0 1 1 0 1
So the combined function nexor outputs a one whenever its two inputs are equal, and a zero when they are not equal. The exor function can be made in the same way as the above construction, filling in the not exor part for all 4 possibilities and simplifying the logical function result:
proc exor {a b} {return [or [and [inv $a] $b] [and $a [inv $b]]]}Basically this says that the output is one for two cases, in(0,1) and in(1,0) and zero otherwise, so we figure out functions that respond with a one on their output for each and exactly each of those input value combinations, and tie them together with an or function, which is one for each of those input selection functions being one, and zero otherwise: Fexor :--> (input_bitstring == 01) || (input_bitstring == 10). We could also figure out a way to have a exor function that essentially returns a boolean (two valued) value based on whether there is an odd number of input bits one (in this case 1 and not zero or 2).
The idea now is to take the above type select functions, and take as many as we need to let each one select out exactly one possible input combination.
Then we apply the whole set of select functions to a chosen domain of binary numbers as n=pow(2,#bits) inputs to a 'combination' function, which generates an output word of m bits for each possible combination of inputs, which are combined into the m bits spanning the output co-domain of any logical function from n to m bits. The or combination combines the outputs of all select functions that make the overall function output bit the 'or' is associated with, which correspond to a logical output of 1. So in fact we take the output range of the logical function at hand, and for each bit we determine which inputs combinations make that output bit a 1, and 'or' the corresponding select intermediate outputs together. We repeat that for each bit of the output range, and reuse the set of intermediate select functions, not implementing those eventually that aren't or-tied at any point.
That is regular digital designer practice, at least those who know what they are doing, and is sometimes called the and-or planes solution. Mathematically, it offers a clean and overseeable construction proof for any binary function from any binary number domain to range. With of course a direct possible extension to formal logic where one can take the boolean 0 and 1 to stand for false and true, and where these constructions cna be used to cover and analyze all possible uses of all propositions.
Finally, we can proof that we can construct ANY logical function by using just NAND gates, by observing that:
inv = nand(1,in) and = not(nand(..)) or = nand(inv(i1),(inv(i2))
RS comments: It is debatable which operations are basic (e.g. NAND or NOR suffice to build all others), but inv above is frequently called not, and should in parallel to and and or be implemented with !, i.e.
proc inv a {return [expr {!$a}]}Also, expr arguments should be braced, for performance and robustness against double substitution. And the use of for above makes my fingers itch - in such a small domain, I'd much rather KISS and write
foreach j {0 1} {foreach i {0 1} {...}}than
for {set j 0} {$j < 2} {inc j} { for {set i 0} {$i < 2} {incr i} {...}}TV: Fine, fine, I was making a point, not doing efficient boolean Tcl... Basic operations follow from the number of possible function mapping from m to n bits, one could chose various basis functions to span that functions space, these are the historic ones, for decent and acceptable reasons, and as I'll write further, on can mathematically proof that the ones I present can form the basis for ANY digital functions.
I just corrected the inv, which is inv because that is what the equivalent hardware unit is called, a 'not' unit doesn't have the same ring to it.
TV 2003-06-29: Rereading, I'm not sure whether the point, which is certainly important, is clear from this. Nand-s are valid basis functions to span any boolean function space, I not sure that is questioned here, but that is true (I mean I'm electrical engineer, did my digital logic courses, and even advaced formal logic course, and am excellent digital designer, and even intimately enough know where the thinking comes from in theoretical physics and functional analysis and the math that sort of grew with that).
Whether, I assume that is the remark, the nand is a good basis is of course debatable, it used to be in the time of ttl circuits that implemented that function well with the transistor transistor circuits it had. Nors ar fine, too. I'm not sure what is preferred in current cmos circuits. The choice is limited, though, for two valued functions there are only 16 possible two input function mappings:
i1 i2 out 0 0 a 0 1 b 1 0 c 1 1 d
where we can set the word formed by abcd to pow(2,4) = 16 possibilities, of which defined are and, or, xor, and if we take reordering the inputs to be unimportant, that is about it for symmetrical functions, except the null function. Asymmetrical would do for some part of the generalized binary function construction, but they wouldn't all be a possible basis. and inv i1 i2 or the complement would be fine it seems, but isn't usually chosen.
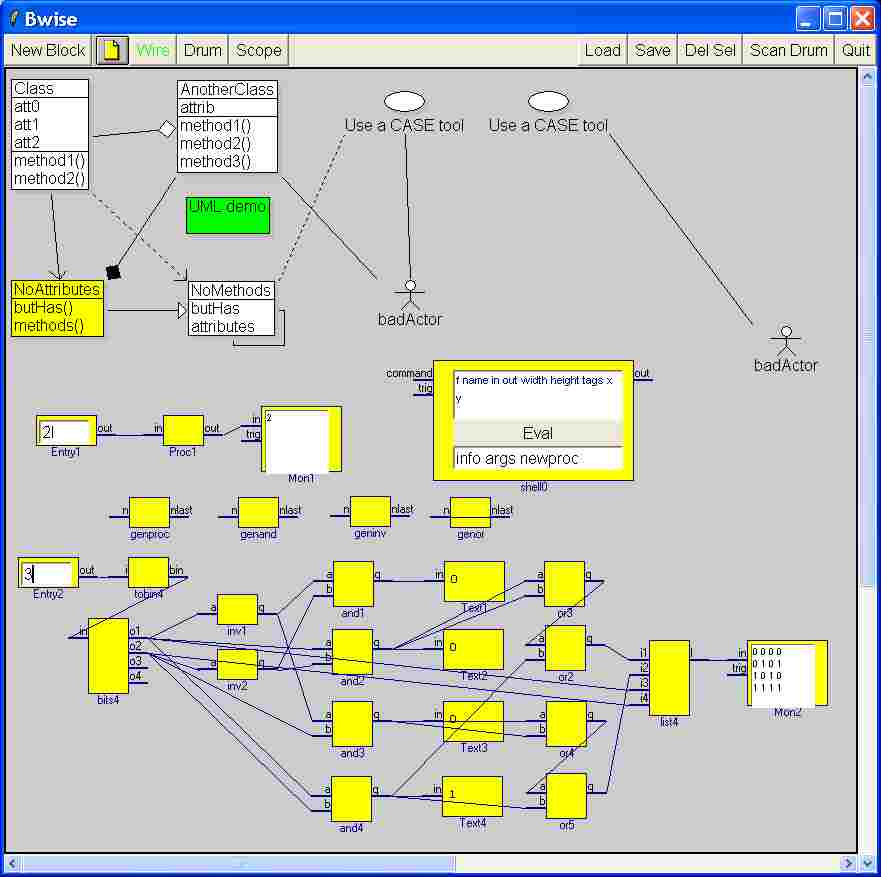
And example of a 2-bit decoder followed by an encoder that codes back to binary, is shown in bwise (bottom part of the image):
The generators for the various logical blocks are (I mean they are blocks that generate other blocks):
newproc "newproc \"set or\${genor.n}.q \\\[expr (\\\${or\${genor.n}.a} || \\\${or\${genor.n}.b})\\\]\" or\${genor.n} {a b} q ;set genor.nlast \${genor.n}" genor n nlast
newproc "newproc \"set inv\${geninv.n}.q \\\[expr !(\\\${inv\${geninv.n}.b})\\\]\" inv\${geninv.n} {a} q ;set geninv.nlast \${geninv.n}" geninv n nlast
newproc "newproc \"set and\${genand.n}.q \\\[expr (\\\${and\${genand.n}.a} && \\\${and\${genand.n}.b})\\\]\" and\${genand.n} {a b} q ;set genand.nlast \${genand.n}" genand n nlastAs shown in the image, these are blocks that can be 'eval'-ed using the popup menu, or the button in the 'data' window, to generate blocks of and, or and inv kind. As shown with genor, we can initialize the input to count 0 or 1, and wrap back the output to the input after changing the block function code to increment the counter with one. Then we can call 'funprop' on the single blocks with feedback, and we get incrementing indices when generating logical blocks.
The generated and or and invert blocks can be dragged in place on the canvas and connected.
Some special blocks with general applicability
newproc {binary scan [binary format S ${tobin4.i}] B* ba ; set tobin4.bin [lrange [split $ba {}] end-3 end]} tobin4 i bin
newproc {for {set i 0} {$i <4} {incr i} {set bits4.o$i [lindex ${bits4.in} $i]}} bits4 in {o1 o2 o3 o4} The connections can be taken from
netlistout
{Entry1 out Proc1 in} {Proc1 out Mon1 in} {genor nlast genor n} {or2 q list4 i1} \
{or3 q or2 a} {inv1 q and1 a} {inv1 q and3 a} {inv2 q and1 b} {inv2 q and2 b} \
{and1 q Text1 in} {and2 q Text2 in} {and2 q or3 a} {and2 q or3 b} \
{bits4 o1 inv1 a} {bits4 o1 and2 a} {bits4 o1 and4 a} {bits4 o1 list4 i3} \
{bits4 o2 inv2 a} {bits4 o2 and3 b} {bits4 o2 and4 b} {bits4 o2 list4 i4} \
{and3 q Text3 in} {and3 q or4 a} {and3 q or4 b} {and4 q Text4 in} {and4 q or2 b} \
{and4 q or5 b} {tobin4 bin bits4 in} {Entry2 out tobin4 i} {or4 q or5 a} \
{or5 q list4 i2} {list4 l Mon2 in}I should have the bwise file somewhere, I'll see.
The idea in bwise is that the variables in a block are available in the 'data' window, and the names are subpaths of the block names, and that apart from input and output pins there is limited state and other dependence outside the obvious for such a block.
The funprop popup menu makes the data ripple through the blocks as if they are functions, which in this example works fine.
The idea of function decomposition in tcl is valid to dwell upon a bit. Suppose we have some function f:
proc f $inputs $body {
# lots of things
return \$result
}Suppose we know the domains of all the inputs, like we would have as an example:
set inputs number1 number2 operation
set number_range {1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16}
set operation_range {zero select1 select2 add subtract multiply divide modulo clip}with
set number1 1
set number2 33
set domainok 1
foreach n {1 2} {
eval set nn \$number$n
if {[lsearch $number_range $nn] <0 } {
puts "invalid input number value: $nn for number$n"
set domainok 0
}
}
;# --> invalid input number value: 33 for number2When domainok is one after this, we should do the same for the operation argument, and we have made sure we defined the whole domain of all its arguments, and tested whether a certain case is in or certainly not in that domain.
Now we can make the maybe cartesian product or let's just say combined 'input' of our function, which isn't defined yet, as:
set one_unique_valid_input $number1_$number2_$operation
Where we have to go over all possible combination to strictly and accurately define our function:
set inputs {number1 number2 operation}
set number_range {1 2 3 4}
set operation_range {add multiply}
set operation_translate(add) +
set operation_translate(multiply) *
set function "set input \$number1\\_\$number2\\_\$operation ;\n switch \$input "
foreach number1 $number_range {
foreach number2 $number_range {
foreach operation $operation_range {
set input $number1\_$number2\_$operation
append function "$input {return [eval expr \$number1 \$operation_translate($operation) \$number2]} "
}
}
}
proc f $inputs $functionNow we can call our function which unravels all input combinations we defined as valid:
f 1 1 add 1 f 4 4 multiply 16
VI 2004-02-15: To address TV's above - "I'm not sure what is prefered in current cmos circuits". In the most common digital CMOS logic, a NAND is always preferred. For a given area the PMOS (or the pull-high part of the gate) is weaker than the NMOS (or the pull-low) part of the gate. In a NAND gate, the PMOS transistors are in parallel (so their strengths add up) and the NMOS are in series (their strengths do not add up). This gives the smallest area with somewhat equivalent rise time and fall times. This is a simplistic, but correct explanation. See slide 4 in http://kritor.openhand.net/hmv/datasheets/PLDs/EE121Lec02.pdf .
RS: gets reminded of the generic Boolean proc that takes a truth table, and can be "specialized" by aliasing (from the NAND page):
proc booleanFunction {truthtable a b} {lindex $truthtable [expr {!!$a+!!$a+!!$b}]}
interp alias {} and {} booleanFunction {0 0 0 1}
interp alias {} or {} booleanFunction {0 1 1 1}
interp alias {} nand {} booleanFunction {1 1 1 0}!! is a cute little Booleanizer (thanks KPV on Toggling a Boolean variable!)
---
JCLyke humbly submits another take on representations of arbitrary Boolean functions and simple cellular automata Boolean Functions and Cellular Automata
TV 2005-10-36: To make things clear in terms of essential computer circuits which were essential for the success of logical circuits and systems and algebra, I'm making a page on Bwise, a serial port tcl script and a Xilinx demo board to make clear in practice what basic logical circuits work like in modern technology...
DKF 2011-11-11: Here's another way to produce truth tables (with mad code synthesis skillz!).
package require Tcl8.5
puts -nonewline "Enter a boolean expression: "
flush stdout
set exp [gets stdin]
set vars [lsort -unique [regexp -inline -all {\$\w+} $exp]]
set cmd [list format [string repeat "%s\t" [llength $vars]]%s]
append cmd " {*}\[[list subst $vars]\] \[[list expr $exp]\]"
set cmd "puts \[$cmd\]"
foreach v [lreverse $vars] {
set cmd [list foreach [string range $v 1 end] {0 1} $cmd]
}
puts [join $vars \t]\tResult
apply [list {} $cmd]Sample run:
Enter a boolean expression: ($a&&$b)||$c $a $b $c Result 0 0 0 0 0 0 1 1 0 1 0 0 0 1 1 1 1 0 0 0 1 0 1 1 1 1 0 1 1 1 1 1