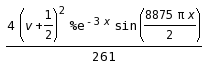Constructing a Bwise Graph from a Maxima Formula

Maxima is a Free and Open Source mathematical language running on a LISP interpreter for which there are Tcl bindings and a Tk interface, I've a few pages on how to use it with tcl, and in this case I'd like to make maxima formulas, for instance for signal processing, into a graph by using tcl and maxima combined.

An example formula is an addition of variables and numbers, like:

output = in1 + (3 + in2)

for no particular reason, in this example, which could be seen as a single bwise block with three inputs and one output, the main operator is addition. Of course this is often the case, but a random mathematical function or formula (lets assume with one output or result or result variable) often as an addition as top level operator.

What I'd like to do, and automatically too is to make blocks for each level of the formula evaluation, in the above case in1 +() and 3+in2.

In Tcl I did something of the kind once (constructing a bwise graph from a formula), but I didn't like it enough, so I don't go into that, but I want to do some work on getting a random maxima formula correctly decomposed in blocks. I can already do the converse at "string=formula" level with substitutions.

The idea is to use a maxima formula deconstruction function, repeatedly driven from tcl and than have bwise automatically create and place the blocks.

First, to separate a maxima stated formula (any formula in principle) into components:

proc domaximapart { {m} } {
    set t "display2d:false;partswitch:true;\n$m;"
    # return [string range [exec maxima << $t | tail -2  ] 6 end-7]
    return [string range [exec maxima -q << $t ] 43 end-7]
    #return [exec maxima --real-quiet << $t ]
} 

#return a list in the form {operator arg1 arg2 ...}
proc maxcompo1 { {a} } {
    set o [domaximapart part($a,0)]
    if [string equal \{\" [string range $o 0 1 ]] { set o [string range $o 2 end] }
    if [string equal \"\} [string range $o end-1 end]] { set o [string range $o 0 end-2] }

    set i 1
    while {![string equal [set k [domaximapart part($a,$i)]]  "end"]  & $i<40} {
#       puts $i,$k
#       flush stdout
#       update
        lappend o $k
        incr i
    }
    if {$i>= 40} {return error}
    return $o
} 

The above formula gives the result:

% maxcompo1 {in1 + (3 + in2)}
+ in2 in1 3

An addition operator (first argument) with 3 arguments. Another example, where maxima will do computations and simplifications first (like it normally always does), before doing the argument separation:

% foreach i [maxcompo1 {diff(sin(x)^2-1^2,x)}] {puts $i}
*
2
cos(x)
sin(x)

a multiplication of three components.

Now we can repeatedly call this function, apply it recursively or looped on its output list elements, make nicenames for the standard operators (probably Tk doesn't like labels like + and /) create blocks for each operator with the right number of input connectors, and connect them in the right structure, according to the basic functional decomposition.

# Create a new bwise block for an operator with nin inputs
proc newop { {op {+}} {nin {2}} {name {}} {in {in}} {out {out}} {width {40}} {height {}} {tags {}} {x {10}} {y {10}} } {
    if {$name == {}} {
        switch -- $op + {set name add} - {set name sub} \/ {set name div} * {set name mul} ^ {set name pow} default {set name $op}
        uplevel #0 {if {[info exists proccount] == "0"} {set proccount 0} ;}
        global proccount
        incr proccount
        append name 0$proccount
    }
  
    set inp "\{"
    set f  "\{set $name.$out \""
    if {$nin == 1} {
        append inp " in"
        append f  "\($op\(\$\{$name.in\})"
    } {
        append inp " in0"
        append f  " ( (\$\{$name.in0\})"
    }
    for {set i 1} {$i < $nin} {incr i} {
        append inp " in$i"
        append f  " $op (\$\{$name.in$i\})"
    }
    append f  ")\"\}"
    append inp " \} "
    puts   "$f $name $inp $out $width {} {} $x $y"
  
    eval "newproc $f $name $inp $out $width {} {} $x $y"
    return $name
} 


# turn a maxima formula to blocks for the highest operator, with pins containing the leaf-decompsition parts, recursive, no graphics layout yet
proc maxtoblock { {a} {rec {0}} } {
    incr rec
    if {$rec > 10} {return error}
    set r [maxcompo1 $a]
    if [string equal $r end] {return end}
    set op [lindex $r 0]
    set r [lrange $r 1 end]
    set name [newop $op [llength $r]]
    if {[llength $r] == 1} {
        set name2 [maxtoblock $r]
            if ![string equal $name2 end] {connect {} $name in $name2 out} {
                uplevel #0 set $name.in $r
            }
    } {
        set j 0
        foreach i $r {
            set name2 [maxtoblock $i]
            if ![string equal $name2 end] {connect {} $name in$j $name2 out} {
                uplevel #0 set $name.in$j [lindex $r $j]
            }
            incr j
        }
    }
    return $name
} 

The above procedure is recursive, will as is descend 10 levels into a formula of maximally 40 components per layer, and isn't particularly fast since its calls maxima repeatedly for each component of the formula, so a linux systems preferably tuned to exec maxima is prefered. I tried some small and some bigger formula examples which appear to work correctly.

I tried this formula as bigger example coming from my sound formula examples:

4*(v+1/2)^2*%e^-(3*x)*sin(8875*%pi*x/2)/261

prettyprinted:

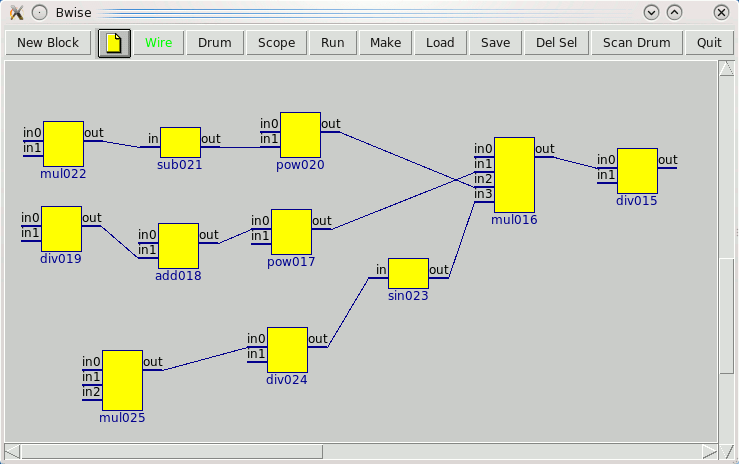
I used

maxtoblock ${sineexp5_2.out}

where sineexp5_2.out contains the string with the formula, and got this structure, after dragging the blocks into place:

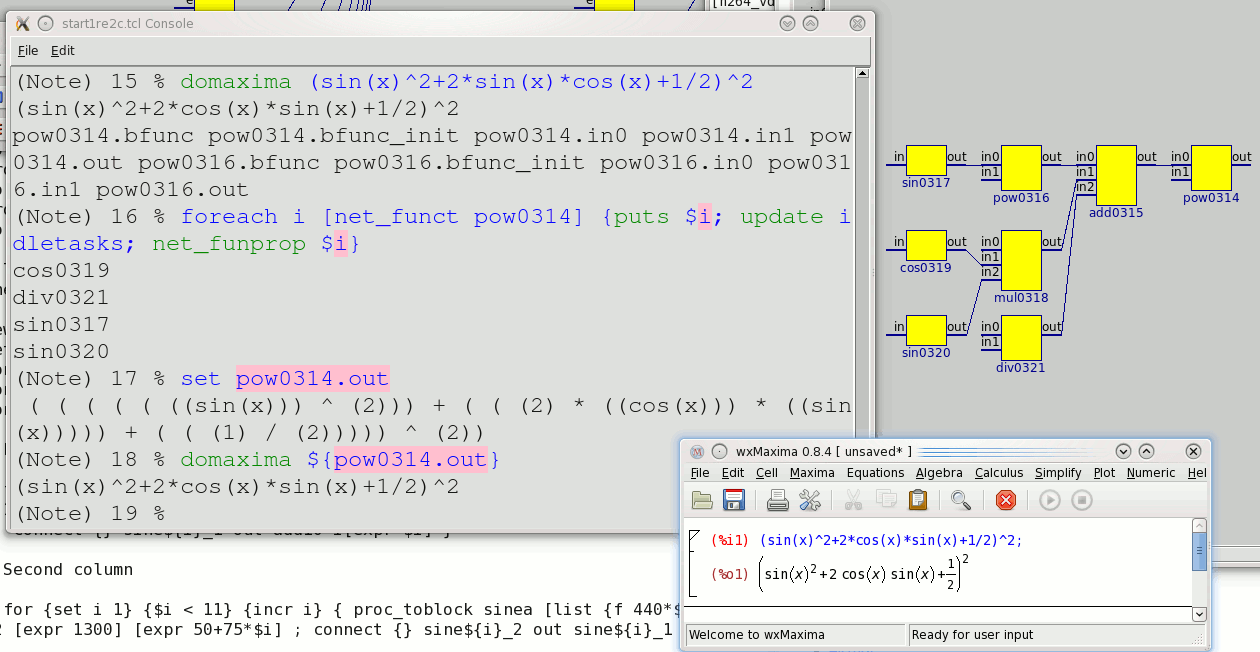
To test the resulting structure, I did

foreach i [net_funct div015] {net_funprop $i; update}

to pass all information from all the inputs to the output of the subgraph, and now we can check if the same formula has been constructed, after rearranging all the added braces:

% domaxima ${div015.out}
4*(v+1/2)^2*%e^-(3*x)*sin(8875*%pi*x/2)/261

Voila!

On to a automatic graphics structure, probably based on recursion level. This is an updated (the above is probably easier to follow as it follows standard recursive programming ideas) versionw to put blocks in place on the canvas. It doesn't take block size into account, and makes generally often wrong assumptions about the formula structure, but at least for a number of cases ot will even generate a correct (non-overlapping, decent shape) graph:

proc maxtoblock { {a} {rec {0}} {x {700}} {y {50}} } {
    incr rec
    if {$rec > 20} {return error}
    set r [maxcompo1 $a]
    puts $r
    if {$r eq {end}} {return end}
    set op [lindex $r 0]
    set r [lrange $r 1 end]
    set name [newop $op [llength $r] {} in out 40 {} {} $x $y]
    update
    if {[llength $r] == 1} {
        set name2 [maxtoblock $r $rec [expr {$x-95}] $y]
        puts $name2
        if {![string equal $name2 end]} {
            connect {} $name in $name2 out
            incr y 85
        } {
           uplevel #0 set $name.in $r
        }
    } {
        set j 0
        foreach i $r {
        set name2 [maxtoblock $i $rec [expr {$x-95}] $y]
        puts $name2
        if {![string equal $name2 end]} {
            connect {} $name in$j $name2 out
            incr y 85
        } {
            uplevel #0 set $name.in$j [lindex $r $j]
        }
        incr j
    }
}
flush stdout
update
    return $name
} 

Also some debugging (which proved unneeded) statements were added. I tried the above out:

Works correctly. Also, I tried one of my medium sized examples about generating waves out with the graphical version to form a graph automatically with a few hundred blocks, which went of the screen because of the size: the end result of firing the blocks and gathering up the formula back from the automatically generated graph was correct, after using maxima as a formula canonizer, the result appears to be exactly the same, so that now a canvas can be composed into a formula, and a formula rendered as a graph on a canvas.

Using A simple BWise to VHDL example and C math functions with braces the resulting graph can also be used to generate vhdl math and C math functions automatically. For vhdl I need to generate interface statements automatically (a little work) and it might be a little low level (sine fuinctions in vhdl may be troublesome) and the C compiler will have to agree with bracing every part of an equation and dealing with that accordingly, which I'm not totally sure about, but I suppose gnu cc will do that ok. So a forumla can then from a bwise graph be put into hardware or software compuations automatically.

The next thing is to make some great tcl functions to deal with refactoring maxima expressions, or possibly some subset of tcl procs or math functions, like searching for subexpressions and taking hierarchical formul levels aparts (wcich given the above works is good in maxima, albeit slow at the moment (see my tradaof between calling maxima issues: two processes (pipe conext swithch time), internal om-compiled tcl/tk (immediate), calling maxima (exec/(re)fork, stdio)).