Dragon Counting Dice Game V3 , dice procedure algorithm and TCL 8.6 demo example calculator, numerical analysis
This page is under development. Comments are welcome, but please load any comments in the comments section at the bottom of the page. Please include your wiki MONIKER and date in your comment with the same courtesy that I will give you. Aside from your courtesy, your wiki MONIKER and date as a signature and minimal good faith of any internet post are the rules of this TCL-WIKI. Its very hard to reply reasonably without some background of the correspondent on his WIKI bio page. Thanks,gold 20FEB2024
- Preface
- Introduction
- Body
- Test Deck
- TCL is a powerful and versatile language
- Start with a working TCL math template or TCL math subroutine to modify it
- Comparison of the Algorithm(s)
- Stick Dice
- Push Button Operation
- Ways to Improve Efficiency of the TCL code
- Useful Feedback
- Conclusions
- Table 1: Table for 6 sided single die mass probability function
- Table 2: Table for two 6-sided dice, mass probability function
- Table 3: Table for two 2-sided dice, mass probability function
- Table 4: Table for two 20-sided dice, section of mass probability function
- Table 5: List of casts on dice 64
- Testcases Section
- Screenshots Section
- figure 1a. Dragon Counting Dice Game V2 vaporware screenshot
- figure 1b. Dragon Counting Dice Game 20 sides2
- figure 2. Chinese Numbers
- figure 3. Favorite camera on child, commercial game
- figure 4. from Wikipedia, Snakes and Ladders probability after N Turns, commercial game
- figure 5. from Wikipedia, Dragon Counting Dice Game V2 child snake ladder chase game jain
- figure 6 . from Wikipedia, Dragon Counting Dice Game V2 child snake ladder chase game illustration
- figure 7 . replicas , Dragon Counting Dice Game V2 6 sided single die mass probability function
- figure 8 . from Wikipedia, Dragon Counting Dice Game V3 two 6-sided dice mass probability function
- figure 9 . from Wikipedia, Dragon Counting Dice Game V3 6 2-sided stick dice for 64 space
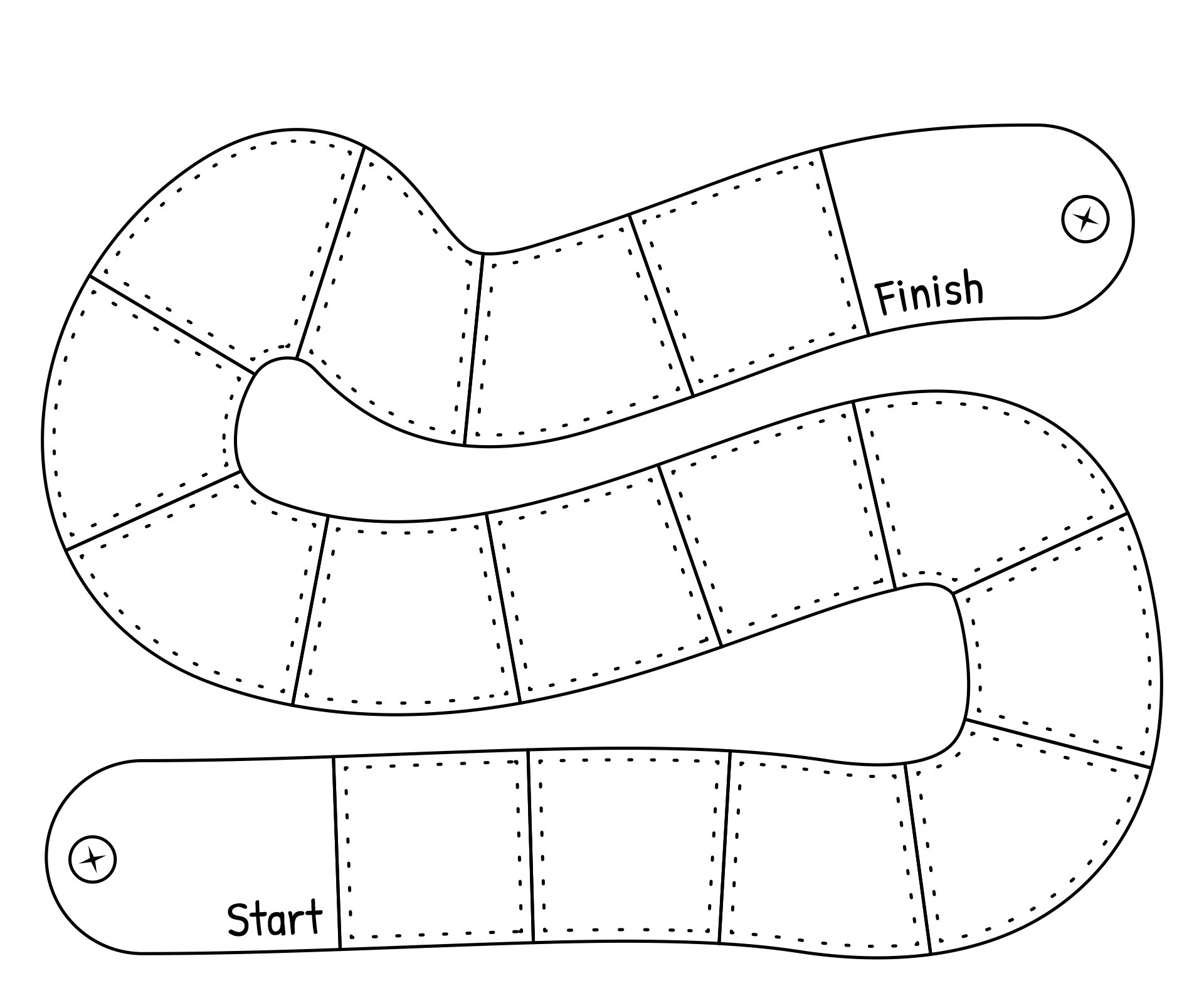
- figure 10 . from Wikipedia, Dragon Counting Dice Game V3 child snake ladder chase game board
- figure 11. Stick Dice
- figure 12. Chinese Abacus
- figure 13. Replica Sundial with Hexagram Marks
- figure 14. Stick Dice
- Screenshots Section
- References:
- Pseudocode & Equations Section
- Appendix Code
- Console program for quantity_into_ratios
- Console program for geometric_mean
- Comments Section
Preface
gold Here are some TCL scripts on the Dragon Counting Dice Game. I found some references on probability for the Snake and Ladder game. Aside from the TCL calculator shell or graphics user interface gui, separate console programs were developed to dump the tables and check the algorithms as independent TCL procedures. These auxlilary decks are used to proof features or subroutines of the program.
The author is retired engineer on Windows 11 and no longer has { proofing access } to Unix machines. Unix is respected after use of so many years in engineering, but my wings are lost. The impetus for this calculator was checking some probabilities on the Dragon Counting Dice Game. It is easy enough to plug in formulas/subroutines into the display formats. Most of the checked testcases involve flipping two sided objects like coins ,popsicle sticks, regular box dice, or four sided rectangular dice. This page is more an investigation into the mindset of the Chinese sages, using TCL visual and random subroutines. Note. I did find a useful online IDE, https://www.jdoodle.com/execute-tcl-online/ .
Introduction
You're trapped in a dungeon with a 20-sided die, and a dragon demands that you pick a specific "sweet integer" number and roll a specific total to escape. For example, you choose the number 42, and if you succeed, you can leave the dungeon. If you fail, you'll be stuck with the dragon or face the dragon penalty box.
Checking math. Gist. In the cited scenario for the Dragon Counting Dice Game, one must choose a "sweet number" to roll on a 20-sided die to escape. The concept of a "sweet number" in this context refers to an integer that, when rolled on the die, results in your escape from the dungeon. To optimize one's chances, one may use mathematical approximations involving natural logarithms and large numbers to guide your selection of the sweet number. One such approximation involves multiplying the chosen number by a specific constant to determine the optimum choice. Ultimately, the goal is to select a number that increases one's likelihood of success in escaping from the dungeon and avoiding the dragon's penalty box.
The rule of thumb for finding the maximum of a function involving natural logarithms and large values of N is to multiply N by a certain approximation. "Sweet winning number" as optimum number in dragon counting game is reported between N and 2N. As rule of thumb, a mathematician James Munro reported that Sweet Number rule as rounded {(e-1)*N)}. However, 1 plus phi conjugate or rounded {(1.6180339887 * N)} would give equivalent answer in small number field, less than 10. Correction here: the optimal number for the original 20-sided die problem is actually ~35. This is slightly better than the first quibble guess of 42. Mathematician has been fed to the dragon as punishment for this dragonish error. Not sure what significance that a "sweet number" means to the dragon. Maybe all numbers are sweet to the dragon at meal time , short of infinity.
Under Math Check & Review, something may not be accurate? :::: The rule of thumb for finding the maximum of a function involving natural logarithms and large values of N is to multiply N by a certain approximation. This approximation is often used when dealing with functions that have a similar shape to the natural logarithm function. By multiplying N by the approximation, you can get a close estimate of the maximum of the function. This rule of thumb is particularly useful when working with large numbers, as it can save time and computational resources compared to finding the exact maximum. The specific approximation used can vary depending on the context and the function being analyzed. But the specific approximation or optimum generally involves multiplying N by a number expression using 2.718281828, which is the mathematical constant known as Euler's number. To find the maximum of a function involving natural logarithms and large values of N, you can use the approximation method. This involves multiplying N by a certain approximation factor. For example, let's consider the function f(N) = N * ln(N). To find the maximum of this function, you can use the approximation N * ln(N) ≈ (N+1) * ln((N+1)/e), where e is the base of the natural logarithm (approximately 2.71828). By applying this approximation, you can find the maximum value of N that makes the function reach its maximum.
Note. This optimization function is sometimes called expm1(x) = exp(x) − 1.
Evaled at 1, general expression is expm1(x) = exp(x) − 1., exp(1) − 1. = 1.718281828
Body
Under Math Check & Review, something may not be accurate? :::: A Snakes and Ladders Chase game is a variation of the classic board game Snakes and Ladders. In this version, two players or teams race to reach the finish line while trying to avoid getting sent back by the snakes and climb up the ladders. The game can be played on a standard Snakes and Ladders board or by using a customized board with additional rules. To play, each player or team takes turns rolling the dice and moving their game piece along the board according to the number rolled. If a player lands on a ladder, they can move up to the higher square indicated by the ladder. However, if they land on a snake's head, they must move down to the corresponding tail square. The first player to reach the finish line (usually the last square on the board) wins the game. This version of the game adds a competitive and strategic element, as players try to outmaneuver each other while navigating the snakes and ladders. It can be a fun and engaging way to introduce children to basic strategy and probability concepts while enjoying a classic board game.
By engaging in games like Snakes and Ladders Chase, children can learn to think strategically, analyze patterns, and develop their understanding of probability. These skills can be applied to various fields, including science and technology, and can help to prepare young minds for the challenges of the modern world. I hope that games like Snakes and Ladders Chase continue to be enjoyed by children and adults alike, as they provide not only entertainment but also valuable opportunities for learning and personal growth.
Under Math Check & Review, something may not be accurate? :::: The optimization function expm1(x) or exp(x) - 1 is used in numerical analysis, particularly in scientific and engineering applications, where it serves as an alternative to the standard exponential function exp(x). The expm1(x) function computes the value of e^x - 1, which is the difference between the exponential function and 1. This function is particularly useful in situations where the values of x are small, as it provides a more accurate result than the standard exp(x) function in such cases. The exp(x) - 1 function is essentially an approximation of expm1(x), and is used in situations where the precision of expm1(x) is not required, or when the function is not available in a particular programming language or library. Both functions have their specific use cases, and the choice between them depends on the accuracy requirements and the programming environment being used.
Check. The ability to compute the difference between the exponential function and 1 with greater precision when dealing with small values of x can be particularly valuable in situations where even slight inaccuracies can have significant consequences.
The canvas and buttons presented here are largely based on the Simple Canvas Demo by HJG. The random pick algorithm was posted by Suchenworth RS on Horseracing in Tcl. Using the random pick algorithm from Suchenworth RS is an alternate way to simulate dice play and sometimes easier for the non standard dice set ups. Other dice pages are Throwing Two Dice GWM and Dice by Keith Vetter. Also int from RLE has dice expression expr {1 + int(rand()*6)} RLE. Several Dr. Math emails may reduce some dice issues to simple paths. another useful wiki page was Counting Elements in a List from RWT.
The units can be changed in the internal calculator formulas as TCL code. Any convenient and consistent output units might be used like millimeters, inches, cubits, feet, or dollars to donuts.
Test Deck
I did find a useful online IDE, https://www.jdoodle.com/execute-tcl-online/ . I can paste from local text file, edit, and run a test deck of TCL. I guess we should stop computing chain and endless loop after so long, but kind of interested in looking at the trajectory of sum of random throws. I guess there are lower bounds and upper bounds in the sum of dice throws. Planned to offer section of dice sides, other than one 20-sided die. One might wonder how one can win and lose at same time. "take the money and run" was the old saying, keep playing longer and empty wallet.
gold 2/20/2024 update. A console program has been modified to check the results and timing of one liner procedures in the script. The user can add new algorithms by adding a new one liners program in the source code. One add a number line to the if statement that controls the algorithm selection in the console program. The one liner procedures and solutions can also be pasted into the TCL console easily. The accuracy of these individual solutions varies with the number of trials and some algorithms used are fairly slow, even glacial closers. Most of the one liners programs and usage examples should be pastable into the TCL console.
TCL is a powerful and versatile language
Received useful and constructive feedback from offsite, thanks to @Ava______. Some text rephrasing to apply as general advice to most TCL programs.
Under Math Check & Review, something may not be accurate? :::: Tool Control Language (TCL) is a programming language used in automation, especially in industrial automation and manufacturing. It is designed to control various tools, machines, and processes, allowing for precise and efficient execution of tasks. TCL is based on the IEC 61131 standard, which is an international standard for programming languages used in industrial automation. It is a high-level, text-based language that provides a clear and concise way to describe actions and sequences, making it easier for automation engineers to develop and maintain control programs. TCL can be used to program a wide range of devices and systems, including PLCs (Programmable Logic Controllers), robots, CNC machines, and other industrial equipment. By using TCL, manufacturers can optimize their production processes, reduce human error, and improve overall efficiency and productivity. Some key features of TCL include:
1. Structured programming: TCL supports structured programming concepts, such as IF-THEN-ELSE statements, FOR, Foreach, and WHILE loops, and functions, which enable the creation of modular and reusable code.
2. Data types: TCL supports various data types, including integers, floats, strings, and arrays, allowing for the manipulation and storage of different types of data.
3. Input/Output operations: TCL provides functions for reading and writing data from/to various sources, such as sensors, actuators, and data storage devices.
4. Timers and counters: TCL includes functions for creating timers and counters, which can be used to control the timing of actions and sequences.
5. User-defined functions: TCL allows users to create their own functions, which can be used to encapsulate and reuse common code sequences.
Overall, TCL is a powerful and versatile language for controlling industrial tools and processes, making it an essential tool for automation engineers and manufacturers.
Start with a working TCL math template or TCL math subroutine to modify it
Received useful and constructive feedback from offsite, thanks to @Ava______. Some text rephrasing to apply as general advice to most TCL programs.
To start with a working TCL math template from TCCLIB and modify it for a new purpose, follow these 6 steps:
1. Choose a TCL math template or TCL math subroutine, for example in the TCLLIB library: Find a suitable TCL math template that closely matches the functionality you want to achieve. You can find various templates online or in TCL programming books and resources.
2. Understand the template: Carefully read and understand the template's code, comments, and structure. This will help you identify the parts of the code that you need to modify to create your new purpose.
3. Identify the necessary modifications: Determine the specific changes you need to make to the template to achieve your desired functionality. This may include modifying input parameters, changing calculations, or altering the output format.
4. Modify the template code: Begin modifying the template code, following the guidelines provided by the TCL programming language. Make sure to update any comments or documentation to reflect the new purpose of the subroutine.
5. Test the new TCL subroutine: After making the necessary modifications, test the new TCL subroutine in a console program to ensure it functions as expected. This will help you identify and fix any errors or issues before integrating the subroutine into a graphical user interface (GUI).
6. Load the new TCL subroutine into a GUI: Once the new TCL subroutine has been tested and verified, you can load it into a GUI program that supports TCL scripting. Make sure to follow the GUI's documentation and guidelines for integrating TCL subroutines.
By following these steps, you can successfully start with a working TCL math template, modify it for a new purpose, and then load the new subroutine into a GUI program for further use.
Comparison of the Algorithm(s)
To make a chicken, it is said that God starts with nothing and makes a chicken, 0 --> 1. To make a chicken, man starts with two chickens and the two chickens make a chicken, 2 --> 3.
For global logic flags, the effect is cosmetic, but the flags keep confusion and gritty details out of the final accounting statements. Once the flags are set global, the flags can be reported and evaluated at all subsequent points in the subroutine. The flags can even be sent outside the subroutine with possible global statements as, global loss_this_year. In executive decisions, potential loss must be a factor.
Under Math Check & Review, something may not be accurate? :::: The approximation N * ln(N) ≈ (N+1) * ln((N+1)/e) is a well-known result in mathematics, where e is the base of the natural logarithm. It is often used in number theory and analysis. The golden ratio, on the other hand, is a mathematical concept that is found in nature and art. It is often denoted by the Greek letter phi (φ), and can be calculated as (1 + √5) / 2 ≈ 1.6180339887. It has many interesting properties, and is often used in art and design to create aesthetically pleasing compositions. expm1(x) is a mathematical function that is used to calculate the exponential of a number minus 1. It is often used in numerical analysis and scientific computing. The formula 1 plus phi conjugate {(1.6180339887 * N)} is a way of rounding a number to the nearest multiple of the golden ratio. It is often used in geometry and design, and can be used to create patterns and shapes that are pleasing to the eye.
Under Math Check & Review, something may not be accurate? :::: A single six-sided die has six equally likely outcomes, each with a probability of 1/6. The probability function for a single dice roll is: P(x) = 1/6, for x = 1, 2, 3, 4, 5, 6 This means that the probability of rolling any specific number (1 through 6) on a single dice roll is 1/6, or approximately 16.67%. A double six-sided die has 36 equally likely outcomes, each with a probability of 1/36. The outcomes are determined by the sum of the two dice rolls, ranging from 2 (both dice showing 1) to 12 (both dice showing 6). The probability function for a double dice roll is: P(x) = 1/36, for x = 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 This means that the probability of rolling any specific sum (2 through 12) on a double dice roll is 1/36, or approximately 2.78%.
Under Math Check & Review, something may not be accurate? :::: I am not sure how to define winning at dice games. It is said that some game players need to win one out of three games to keep interest up. Seems to be a common strategy in planning dice games, but it's not a hard rule or requirement for all games. It's based on the idea that players need to win occasionally to maintain their interest and enthusiasm in the game. In many dice games, winning one out of three games can be a good guideline to keep the game balanced and enjoyable for all players. However, this can vary depending on the specific game, the players' preferences, and the dynamics of the game. Some games might require more frequent wins to keep players engaged, while others might allow for longer streaks of losses without losing interest. Ultimately, it's up to the players to decide the frequency and conditions of winning that best suit their preferences and the game they're playing.
Stick Dice
The Iching is the ancient fortune telling book of China. The Iching literature mentions various methods for casting fortune patterns of Iching. The various methods include hot ironing of turtle shells (-t.), manipulations of yarrow sticks, flipping coins, throwing shaman bones, and dice. One analogy from North America is a shaman throwing or shuffling stick dice.
I made three stick dice for Iching by cutting a dowel of square cross section into three sticks. For the three stick dice, the flat sides are marked or burned with 2 or 3 holes alternately. Two sticks are marked with {3 2 3 2} dots on the sides. One stick is marked with {3 3 3 2} dots on the sides. In casting such three dice, the possible sums are 6,7,8, or 9. Further, the stick dice are cast six times to obtain whole lines or broken lines in a pattern or set of six lines. A set of six Iching lines is called a gua in the orient or a hexagram in some translations of the Chinese.
In the Iching interpretations, casts of 6 and 8 are broken or yin (female) lines, while casts of 7 and 9 are whole or yang (male) lines. The casts are recorded by pencil with the first line at bottom and marking up the column. It is possible to record the numbers from the casts with tally sticks or Chinese counting rods, which are somewhat reminiscent of the Iching patterns themselves. After marking the original pattern or hexagram, sometimes a second follow-up hexagram is developed by swapping throws of 6 for a 7 and throws of 9 for a 6. These swaps effectively trade a broken line(6) for a whole line(7) and a whole line(9) for a broken line(6). The throws for the changing lines (6&9) may not always be come out in the first hexagram or its component lines, so the followup hexagram may not exist {under consistent rules}. If the first hexagram is interpreted on a line by line basis, any changing lines(6&9) or second hexagram offers some modification or discount on the interpretation of the first hexagram.
In developing a computer program or application, it is helpful to develop analogs for the individual tasks of the application. An Iching application would have to compose, beg, or borrow TCL procedures for random casts, tallies of scores, accounting files, display hexagram lines on a screen, swapping changing lines, hexagram pattern recognition and ranking interpretations. In fact, some TCL one liner procedures and text swapping routines might be useful as utilities in a starter application program, since unruly text strings are expected in the Iching. Casting the sticks or bones for each Iching line is analog for random lpick subroutine below. Adding the top sides of three sticks and throwing six times is analog for the "for 6 times" statement in the bonereadxx procedure below. In the West, Leibniz etc recognized that the whole and broken lines in the hexagram patterns could be counted as ones and zeros, respectively in a binary number system. For example, a cast or TCL list of { 6,7,8,9,6,7 } could be expressed as a binary number, 010101. The binary numbers are the analogs for the binaryexchange subroutine below. For computer procedures, the patterns are effectively a horizontal bar code of 6 lines.
In the process of designing the basic subroutine tasks, we could throw in some switches, logic chains, or daisy chains that break the outset rules given above. For example, TCL is so good at swapping lines (6&9) for the second hexagram, that it would be easy to put a switch that generates or swaps all hexagram lines (6,7,8,&9) for their opposites. Also from some scripts of the Chinese Chou dynasty, different Iching fortune methods of yarrow sticks or coins would generate different probabilities of obtaining each hexagram line. Might be interesting to have a back door in the program to check (or adapt} the different probabilities of stick or coin throws.
Under Math Check & Review, something may not be accurate? :::: The probability of rolling a specific hexagram, which is a combination of six trigrams, on the Yi Jing, also known as the I Ching, is 1/64. This is because each trigram has 8 possible outcomes (4 broken lines and 4 solid lines), and when you roll two dice, you have 64 possible outcomes (8 x 8 = 64). To roll a specific hexagram, you need both dice to land on the specific trigrams you want, which is 1/64. >>>> I understand your point.<<<<< Probability theory is indeed based on the assumption that events are random, and it provides a framework for predicting the likelihood of different outcomes. If those phenomena are non-random, then the concept of probability and random outcomes may not apply. In the context of the Yi Jing or I Ching, the focus is often on exploring the possible outcomes and gaining insights from the results, rather than calculating mere probabilities. The purpose of these Yi Jing or I Ching practices is to provide guidance or understanding, rather than predicting random events.
Push Button Operation
For the push buttons, the recommended procedure is push a testcase and fill frame, change first three entries etc, push solve, and then push report. Report allows copy and paste from console. For testcases in a computer session, the TCL calculator increments a new testcase number internally, eg. TC(1), TC(2)., TC(3), TC(4) etc. The testcase number is internal to the calculator and will not be printed until the report button is pushed for the current result numbers. The current result numbers will be cleared on the next solve button. For comparison of the Babylonian algorithm with conventional Western methods, TCL code will include redundant procs, redundant calculation paths, and printout check formulas to compute product and area.
For testcases in a computer session, the TCL calculator increments a new testcase number internally, eg. TC(1), TC(2) , TC(3) , TC(N). The testcase number is internal to the calculator and will not be printed until the report button is pushed for the current result numbers. The current result numbers will be cleared on the next solve button. The command { calculate; reportx } or { calculate ; reportx; clearx } can be added or changed to report automatically. Another wrinkle would be to print out the current text, delimiters, and numbers in a TCL wiki style table as
puts " %| testcase $testcase_number | value| units |comment |%" puts " &| volume| $volume| cubic meters |based on length $side1 and width $side2 |&"
Ways to Improve Efficiency of the TCL code
Received useful and constructive feedback from offsite, thanks to @Ava______. Some text rephrasing to apply as general advice to most TCL programs.
Here are some ideas to improve the efficiency of your TCL code:
1. Optimize some procedures by reducing their computational complexity. Instead of using the rand function, you can use a faster random number generator like mt_rand 0. Links Note: Refers to RandMT, Mersenne Twister, & random. Now this is of interest.
2. Implement memorization to avoid redundant calculations. For example, you can store the results of procedure calls in variables and reuse them when necessary.
3. Use the foreach loop more efficiently. Instead of iterating over a range of numbers, you can use the lrange command to generate a list of numbers and iterate over that list. SP may mean lrange?
4. Simplify the conditionals in the some procedures by using logical operators and reducing the number of if statements.
5. Consider breaking down the code into smaller, more manageable procedures and functions to improve readability and maintainability.
6. Use TCLs built-in profiling tools to identify performance bottlenecks and optimize the code accordingly.
7. Finally, consider using a more modern version of TCL that has better performance and additional features. As of the time of this writing, TCL8.6 is several years old, and the latest version is 8.6.12.
Useful Feedback
Received useful and constructive feedback from offsite, thanks to @Ava______. Some text rephrasing to apply advice to most TCL programs.
To improve the readability of the TCL code, consider the following suggestions:
1. Use meaningful variable names: Instead of using single letter variable names like 'i', j, m, 'msg', and 'proc', use more descriptive names that help convey the purpose of the variable. This will make the code more readable and easier to understand.
2. Break down complex procedures into smaller procedures, smaller tasks, and functions: Some codes have a single large procedure which performs multiple tasks. It would be better to break down a large procedure into smaller, more manageable functions and procedures that perform specific tasks. This will make the code easier to maintain and debug.
3. Use comments to explain the code: Adding comments to explain what each section of code does can greatly improve the readability and maintainability of the code. Use comments to explain the purpose of the code, any assumptions made, and any caveats or limitations.
4. Use consistent indentation and formatting: Ensure that the code is consistently indented and formatted. This will make it easier to read and understand the flow of the code. Use a consistent style guide for indentation, spacing, and line breaks.
5. Use meaningful error handling: Add error handling to the code to handle unexpected inputs or situations. Use descriptive error messages to help users understand what went wrong and how to fix it.
6. Use version control: Use a version control system like Git to keep track of changes to the code. This will make it easier to collaborate on the code and to roll back to previous versions if necessary.
7. Identify the main TCL version used, dates, and other TCL library dependencies in header comments.
Conclusions
gold Update 2/21/2024. I have found it easier and more tidy to start with a working TCL math template and morf a few lines into a new purpose. If one completes and tests the new TCL subroutine in a console program, then usually one can load the new TCL subroutine into a graphical user interface (gui). I am not sure how to define winning at dice games, other than the pleasure of learning more TCL. It is said that game players need to win one out of three games to keep interest up.
Table 1: Table for 6 sided single die mass probability function
Probability of a certain number with a Single Die.
Roll a single die Probability
| table 1 | Prob. Fraction | Prob. decimal printed in tcl wiki format |
|---|---|---|
| 1 | 1/6 | 16.667% |
| 2 | 1/6 | 16.667% |
| 3 | 1/6 | 16.667% |
| 4 | 1/6 | 16.667% |
| 5 | 1/6 | 16.667% |
| 6 | 1/6 | 16.667% |
Table 2: Table for two 6-sided dice, mass probability function
| table 2 | Prob. fraction | Prob. Decimal | printed in tcl wiki format |
|---|---|---|---|
| 2 | 1/36 | 2.778 | |
| 3 | 2/36 | 5.556 | |
| 4 | 3/36 | 8.333 | |
| 5 | 4/36 | 11.111 | |
| 6 | 5/36 | 13.889 | |
| 7 | 6/36 | 16.667 | |
| 8 | 5/36 | 13.889 | |
| 9 | 4/36 | 11.111 | |
| 10 | 3/36 | 8.333 | |
| 11 | 2/36 | 5.556 | |
| 12 | 1/36 | 2.778 |
Table 3: Table for two 2-sided dice, mass probability function
| Table 3 | printed in TCL WIKI format |
|---|---|
| 1 | 0.0 |
| 2 | 0.25 |
| 3 | 0.5 |
| 4 | 0.25 |
Table 4: Table for two 20-sided dice, section of mass probability function
Note. Checking math here, value for 1 is really null, not zero.
| Table 4 | two 20-sided dice print TCL WIKI format |
|---|---|
| 1 | 0.0 |
| 2 | 0.0025 |
| 3 | 0.005 |
| 4 | 0.0075 |
| 5 | 0.01 |
| 6 | 0.0125 |
| 7 | 0.015 |
| 8 | 0.0175 |
| 9 | 0.02 |
| 10 | 0.0225 |
| 11 | 0.025 |
| 12 | 0.0275 |
| 13 | 0.03 |
| 14 | 0.0325 |
| 15 | 0.035 |
| 16 | 0.0375 |
| 17 | 0.04 |
| 18 | 0.0425 |
| 19 | 0.045 |
| 20 | 0.0475 |
| 21 | 0.05 |
| 22 | 0.0475 |
| 23 | 0.045 |
| section ends |
Table 5: List of casts on dice 64
Note. Checking math here,
2 8 3 20 4 42 5 32 6 51 7 39 8 25 9 13 10 49 11 34 12 26 13 8 14 23 15 11 16 17 17 42 18 54 19 63 20 40
3 6-sided dice "output 1",10.500000000004832,2.9580398915501926,3,18 #,% 3,0.462962962963 4,1.38888888889 5,2.77777777778 6,4.62962962963 7,6.94444444444 8,9.72222222222 9,11.5740740741 10,12.5 11,12.5 12,11.5740740741 13,9.72222222222 14,6.94444444444 15,4.62962962963 16,2.77777777778 17,1.38888888889 18,0.462962962963
Testcases Section
Testcase 1 , single 6-sided die
The estimated optimum for a 6 sided die is rounded 10. Sum of throws [+ 4 6 3\] or 13 would be a loss.
| table 1 | printed in tcl wiki format | ||
|---|---|---|---|
| quantity | value years | years CE | comment, if any |
| 1: | testcase_number | ||
| 6.0 : | dice sides number, | ||
| 2024.0 : | reference year, birth year, decimal years with decimal fraction : | ||
| 1.0 : | option switch mode, usually 1 for no decay, other modes = 2, 3, 4: | ||
| 3 : | optional constant in other mode, nominal 1 :: | ||
| 1. : | experimental constant_K1 : | ||
| 6.0 : | dice sides number : | 10 ] | 6.0 |
| 4 : | probable 2 next throw : | 10 | win at 6.0 |
| 6 : | probable 3 next throw : | 10 | win at 6.0 |
| 3 : | probable 4 next throw : | 10 | loss |
| 5 : | probable 5 next throw : | 10 | loss |
| 6 : | probable 6 next throw : | 10 | loss |
| 4 : | probable 7 next throw : | 10 | loss |
| 5 : | probable 8 next throw : | 10 | loss |
Testcase 2 , single 6-sided die
The estimated optimum for a 6 sided die is rounded 10. Sum of throws [+ 2 5 3 3\] or 13 would be a loss. iNTERESTING to have successive sums of 13?
| table 2 | printed in tcl wiki format | ||
|---|---|---|---|
| quantity | value years | years CE | comment, if any |
| 2: | testcase_number | ||
| 6.0 : | dice sides number, | ||
| 2024.2 : | reference year, birth year, decimal years with decimal fraction : | ||
| 1.0 : | option switch mode, usually 1 for no decay, other modes = 2, 3, 4: | ||
| 6 : | optional constant in other mode, nominal 1 :: | ||
| 1. : | experimental constant_K1 : | ||
| 6.0 : | dice sides number : | 10 ] | 6.0 |
| 2 : | probable 2 next throw : | 10 | win at 6.0 |
| 5 : | probable 3 next throw : | 10 | win at 6.0 |
| 3 : | probable 4 next throw : | 10 | win 6.0 |
| 3 : | probable 5 next throw : | 10 | loss |
| 1 : | probable 6 next throw : | 10 | loss |
| 3 : | probable 7 next throw : | 10 | loss |
| 6 : | probable 8 next throw : | 10 | loss |
Testcase 3 , single 6-sided die
The estimated optimum for a 20 sided die is rounded 34. Still using the 6 sided die, but Sum of throws were [+ 6 5 2 5 3 6 1\].
| table 3 | printed in tcl wiki format | ||
|---|---|---|---|
| quantity | value years | years CE | comment, if any |
| 3: | testcase_number | ||
| 20.0 : | dice sides number, | ||
| 2024.5 : | reference year, birth year, decimal years with decimal fraction : | ||
| 1.0 : | option switch mode, usually 1 for no decay, other modes = 2, 3, 4: | ||
| 4 : | optional constant in other mode, nominal 1 :: | ||
| 1. : | experimental constant_K1 : | ||
| 20.0 : | dice sides number : | 34 ] | 20.0 |
| 6 : | probable 2 next throw : | 34 | win at 20.0 |
| 5 : | probable 3 next throw : | 34 | win at 20.0 |
| 2 : | probable 4 next throw : | 34 | win 20.0 |
| 5 : | probable 5 next throw : | 34 | win at 20.0 |
| 3 : | probable 6 next throw : | 34 | win at 20.0 |
| 6 : | probable 7 next throw : | 34 | win at 20.0 |
| 1 : | probable 8 next throw : | 34 | win at 20.0 |
Screenshots Section
figure 1a. Dragon Counting Dice Game V2 vaporware screenshot
figure 1b. Dragon Counting Dice Game 20 sides2
figure 2. Chinese Numbers
--- 
figure 3. Favorite camera on child, commercial game
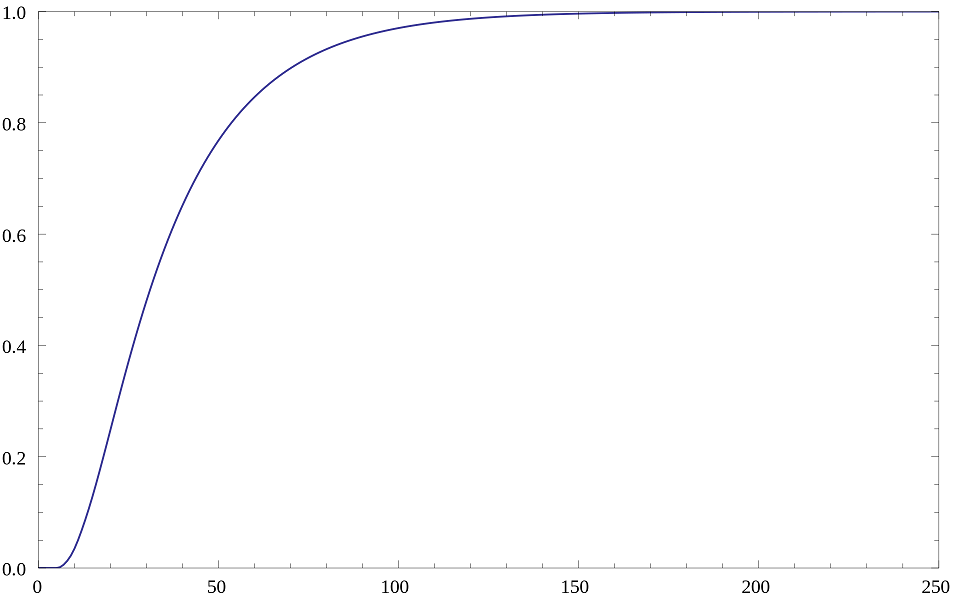
figure 4. from Wikipedia, Snakes and Ladders probability after N Turns, commercial game
Figures the number of turns for completion of Snakes and Ladders game. Y-axis is probability. X-axis is number of turns. Game Completion = 1, I think.
figure 5. from Wikipedia, Dragon Counting Dice Game V2 child snake ladder chase game jain
Gyan chaupar (Jain version of the game), National Museum, New Delhi, credit Nomu420 on Wikipedia. The association of Britain's snakes and ladders with India and gyan chauper began with the returning of colonial families from India during the British Raj. The décor and art of the early English boards of the 20th century reflect this relationship.
figure 6 . from Wikipedia, Dragon Counting Dice Game V2 child snake ladder chase game illustration
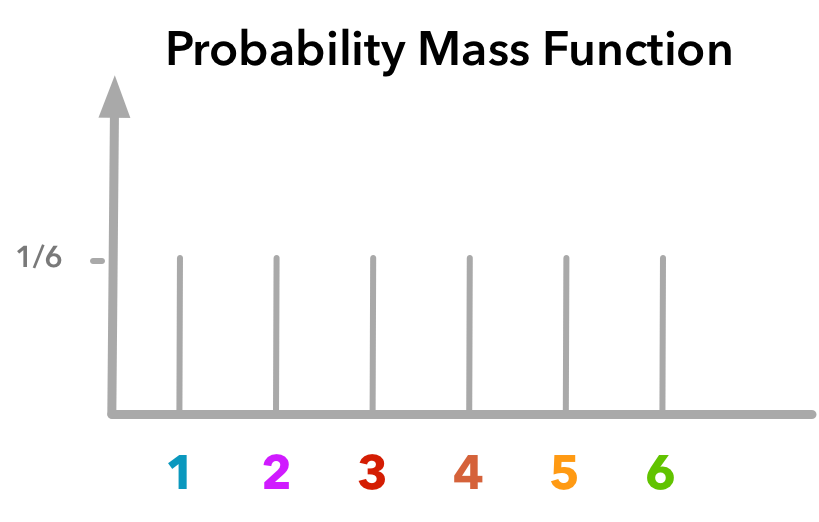
figure 7 . replicas , Dragon Counting Dice Game V2 6 sided single die mass probability function
The probability plot of a 6-sided dice. In the context of a probability plot, we are looking for the probability of each outcome (rolling a 1, 2, 3, 4, 5, or 6) and how they are distributed. Since a fair 6-sided dice is equally likely to land on any of its sides, the probability of rolling each number is the same. For a fair 6-sided dice: The probability of rolling a 1, 2, 3, 4, 5, or 6 is 1/6 or approximately 0.1667. A probability plot for a fair 6-sided dice would show a uniform distribution, with each number having an equal probability of being rolled.
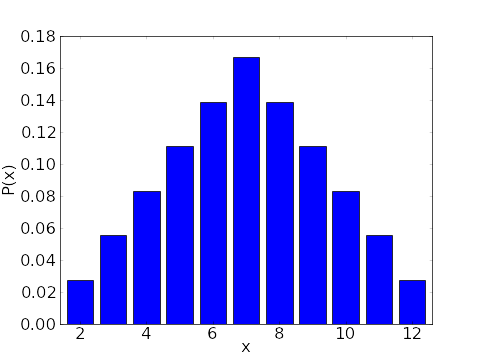
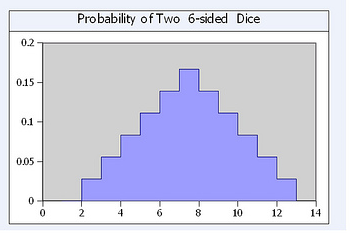
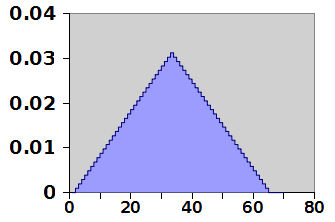
figure 8 . from Wikipedia, Dragon Counting Dice Game V3 two 6-sided dice mass probability function
The probability plot of rolling two 6-sided dice. In the context of a probability plot, we are looking for the probability of each outcome (rolling a 2, 3, 4, ..., 12) and how they are distributed. When rolling two 6-sided dice, the total number of possible outcomes is 6 * 6 = 36. The probability of each outcome is calculated by dividing the number of ways to achieve that outcome by the total number of possible outcomes (36). For example, there is only one way to roll a 2 (rolling a 1 on both dice) and one way to roll a 12 (rolling a 6 on both dice), so the
probability of rolling a 2 or a 12 is 1/36 or approximately 0.0278. Here is the probability distribution for rolling two 6-sided dice: Probability of rolling a 2: 1/36 or approximately 0.0278 Probability of rolling a 3: 2/36 or approximately 0.0556 Probability of rolling a 4: 3/36 or approximately 0.0833 Probability of rolling a 5: 4/36 or approximately 0.1111 Probability of rolling a 6: 5/36 or approximately 0.1389 Probability of rolling a 7: 6/36 or approximately 0.1667 Probability of rolling an 8: 5/36 or approximately 0.1389 Probability of rolling a 9: 4/36 or approximately 0.1111 Probability of rolling a 10: 3/36 or approximately 0.0833 Probability of rolling an 11: 2/36 or approximately 0.0556 Probability of rolling a 12: 1/36 or approximately 0.0278
A probability plot for rolling two 6-sided dice would show a bell-shaped distribution, with the most likely outcomes being rolling a 7, and the least likely outcomes being rolling a 2 or a 12.
figure 9 . from Wikipedia, Dragon Counting Dice Game V3 6 2-sided stick dice for 64 space
figure 10 . from Wikipedia, Dragon Counting Dice Game V3 child snake ladder chase game board
figure 11. Stick Dice
figure 12. Chinese Abacus
figure 13. Replica Sundial with Hexagram Marks
figure 14. Stick Dice
test reload of images from offsite
Screenshots Section
figure 2.
figure 3.
figure 4.
figure 5.
figure 6.
figure. Space probability on space of 64
The probability plot of rolling six 2-sided dice. In the context of a probability plot, we are looking for the probability of each outcome (rolling a 1, 2, 3, ..., 64) and how they are distributed. When rolling six 2-sided dice, the total number of possible outcomes is 2 * 2 * 2 * 2 * 2 * 2 = 64. The probability of each outcome is calculated by dividing the number of ways to achieve that outcome by the total number of possible outcomes (64). For example, there is only one way to roll a 1 (rolling a 1 on all six dice) and one way to roll a 64 (rolling a 2 on all six dice), so the probability of rolling a 1 or a 64 is 1/64 or approximately 0.0156. A probability plot for rolling six 2-sided dice would show a bell-shaped distribution, with the least likely outcomes being rolling a 1 or a 64.
References:
- Primary references, Google <Babylonian Multiplication by M. Lewinter and W. Widulski>
- Mathematics
- Primary reference, Pi is Evil - Numberphile, Featuring James Munro with Dragons, Dice and Evil Numbers.
- James Munro is Admissions and Outreach Coordinator for Maths at Oxford University.
- snakes_probability/snakes_probability ,
- Desmond Higham, Nicholas Higham
- Steve Althoen, Larry King, Kenneth Schilling,
- How long is a game of Snakes and Ladders?,
- The Mathematical Gazette,
- Volume 77, Number 478, March 1993, pages 71-76.
- Nick Berry,
- A Mathematical Analysis of Snakes and Ladders,
- www.datagenetics.com/blog/november
- Dr. Math articles are locked behind pay wall, things getting tough.
- I did find an online IDE, https://www.jdoodle.com/execute-tcl-online/
Pseudocode & Equations Section
more than one formula for 1) tables and 2) calculator shell
# recommended, avoids division by zero
product of 50*40*30 using modern base_60 logarithms,
# used in thinking pod
the sum of logs is expr { 0.95546+0.90096+0.830706} , 2.687126.
The antilog in base_60 is expr 60**2.687126= 59995.193.
For the tables, the int function is used to clip remainders to integers.
the precision function by [AM] is used occasionally, but not every time.
note: mental and undocumented components in the methods.
# exponent/ logarithm expressions
log (sqrt (m)) = (1/2)*log (m)
log (crt (m)) = (1/3)*log (m)
log (sqrt (m)) = (1/2)*log (m)
(1/2) = log (sqrt (m)) / log (m)
(1/2) = log (sqrt (m)) - (m))
log (crt (m)) = (1/3)*log (m)
(1/3) = log (crt (m)) / log (m)
(1/3) = log (crt (m)) - (m))
(1/2) = log (sqrt (m)) / log (m)
(2/1) = log (m) / log (sqrt (m))
2 = log (m - (sqrt (m))
(3/1) = log (m) / log (crt (m))
3 = log (m - (crt (m))
N = log (m - (N’rt(m))
N+1 = log (m - ((N+1)’rt(m))
log2 defined as ln N / ln 2 ,
log2 N =~ 1.442695 * ln N
log2 N =~ 3.321928 * log10 N
# find simple interest amount from 3 entries as < principal interest years >
proc simple_interest_amount { principal interest years } { expr { ($principal*1.)*(1.+$years*$interest )}}
# Dice in alternate procedures, checking math and format here
expr {1 + int(rand()*6)} RLE
# parens? weak eyes here.
proc dice_sides_N { dice_sides } { expr { 1 + int(rand()*$dice_sides)} }
proc dice_sides_N { dice_sides } { expr { 1 + int(rand()*$dice_sides)} }
proc optimum_N { dice_sides } { expr { int(1.718281828 *$dice_sides) }}
proc optimum_G { dice_sides } { expr { int(1.6180339887498948420 *$dice_sides) }}
# set g_constant .6180339887498948420
# golden ratio is 1.6180339887498948420 Appendix Code
Trial Calculator Shell , Mock Up for Dragon Dice Deck V3
# Mock Up for Dragon Dice Deck V3
# pretty print from autoindent and ased editor
# Dragon Counting Dice Game calculator
# rules= throw N-sided dice until => chosen optimum number,
# declare winner or loser
# written on Windows 10
# working under TCL version 8.6
# gold on TCL WIKI, 30jan2024
package require Tk
package require math::numtheory
namespace path {::tcl::mathop ::tcl::mathfunc math::numtheory }
set tcl_precision 17
frame .frame -relief flat -bg aquamarine4
pack .frame -side top -fill y -anchor center
set names {{} {dice sides number :} }
lappend names {reference year, year with decimal fraction: }
lappend names {optional switch mode, usually 1 , other modes = 2, 3, 4: }
lappend names {optional constant , nominal 1 : }
lappend names {answers, probable 2nd next throw, : }
lappend names {probable 3 next throw : }
lappend names {probable 4 next throw : }
lappend names {probable 5 next throw : }
lappend names {probable 6 next throw : }
foreach i {1 2 3 4 5 6 7 8 9} {
label .frame.label$i -text [lindex $names $i] -anchor e
entry .frame.entry$i -width 35 -textvariable side$i
grid .frame.label$i .frame.entry$i -sticky ew -pady 2 -padx 1 }
proc about {} {
set msg "Calculator Dragon Counting Dice Game V2
from TCL WIKI,
written on TCL 8.6 "
tk_messageBox -title "About" -message $msg }
proc self_help {} {
set msg "Calculator for Dragon Counting V2
from TCL ,
# self help listing
# 1 given follow.
1) initial age decimal years N1
2) reference year or birth year
3) optional switch mode, usually 1 for no decay
# optional decay modes = 2, 3, 4, experimental use
4) optional variable decay constant, not used now
# rules= throw N-sided dice until => chosen optimum number,
# declare winner or loser
# For comparison, TCL code may include redundant paths & formulas.
# The TCL calculator normally uses modern
# units for convenience to modern users and textbooks.
# Any convenient and consistent in/output units might be used
# like inches, feet, nindas, cubits, or dollars to donuts.
# Recommended procedure is push testcase and fill frame,
# change first three entries etc, push solve,
# and then push report. Report allows copy and paste
# from console to conventional texteditor. For testcases
# testcase number is internal to the calculator and
# will not be printed until the report button is pushed
# for the current result numbers.
# Use one line errorx proc to estimate percent errors.
# errorx proc is used in the report window (console).
# Additional significant figures are used to check
# the TCL program, not to infer the accuracy
# of inputs and product reports.
# Proc precisionx <AM> is loaded and may be used to
# trim lengthy mantissas.
# precisionx used on select numbers only, not used on every number.
# On variable_cycle, may have to >> exit << to clear registers
# Conventional text editor formulas or grabbed from internet
# Screens can be pasted into green report console.
# Try copy and paste following into green screen console
# set answer \[* 1. 2. 3. 4. 5. \]
# returns 120
# gold on TCL Club, 20feb2024 "
tk_messageBox -title "self_help" -message $msg }
# Dice Sides
# expr {1 + int(rand()*6)} RLE
proc dice_sides_N { dice_sides } { expr { 1 + int(rand()*$dice_sides)} }
proc optimum_N { dice_sides } { expr { int(1.718281828 *$dice_sides) }}
#set g_constant .6180339887498948420
# golden ratio is 1.6180339887498948420
proc calculate { } {
global answer2
global side1 side2 side3 side4 side5
global side6 side7 side8 side9
global side10 side11 side12 winner5
global g_constant gr age_years reference_year
global testcase_number golden_time_cycle
global option_mode optional_constant seed_date
incr testcase_number
set side1 [* $side1 1. ]
set side2 [* $side2 1. ]
set side3 [* $side3 1. ]
set side4 [* $side4 1. ]
set side10 1.
set side11 1.
set side12 1.
set age_years [ expr { $side1*1.0 } ]
set reference_year [ expr { $side2*1.0 } ]
set option_mode [ expr { $side3*1.0 } ]
set optional_constant [ expr { $side4*1.0 } ]
set seed_date [ expr { $side1 + $side2 } ]
set winner5 $side1
# golden conjugate is 0.61803398874989484820
# alternate test value for
# golden conjugate is 0.618
# but do not see much difference on small numbers
# under 20
# initialize golden ratio constants
set gr 1.61803398874989484820
set g_constant 0.61803398874989484820
# test dice section
set side4 [ dice_sides_N 6 ]
set side5 [ dice_sides_N 6 ]
set side6 [ dice_sides_N 6 ]
set side7 [ dice_sides_N 6 ]
set side8 [ dice_sides_N 6 ]
set side9 [ dice_sides_N 6 ]
set side10 [ dice_sides_N 6 ]
set side11 [ dice_sides_N 6 ]
# we have computed the set
# link to proc for study of initial conditions
}
proc winnerx {aa bb} {
global answer2
global side1 side2 side3 side4 side5
global side6 side7 side8 side9
global side10 side11 side12 winner5
global g_constant gr age_years reference_year
global testcase_number golden_time_cycle
global option_mode optional_constant seed_date
#puts "end of game"
#.t insert 1.0 "end of game"
set sumit 0
set winner5 1
set goal [optimum_N $side1]
if { $sumit >= $goal } {
puts "winner declared"
}
}
proc fillup {aa bb cc dd ee ff gg hh ii} {
.frame.entry1 insert 0 "$aa"
.frame.entry2 insert 0 "$bb"
.frame.entry3 insert 0 "$cc"
.frame.entry4 insert 0 "$dd"
.frame.entry5 insert 0 "$ee"
.frame.entry6 insert 0 "$ff"
.frame.entry7 insert 0 "$gg"
.frame.entry8 insert 0 "$hh"
.frame.entry9 insert 0 "$ii"
}
proc clearx {} {
foreach i {1 2 3 4 5 6 7 8 9 } {
.frame.entry$i delete 0 end } }
proc reportx {} {
global side1 side2 side3 side4 side5
global side6 side7 side8 side9 gr
global side10 side11 side12
global testcase_number winner5
global g_constant gr age_years reference_year
global option_mode optional_constant
console show;
puts "%|table $testcase_number| || printed in tcl wiki format|% "
puts "&| quantity| value years |years CE| comment, if any|& "
puts "&| $testcase_number:|testcase_number || |&"
puts "&| $side1 :|dice sides number, | | |&"
puts "&| $side2 :|reference year, birth year, decimal years with decimal fraction : | | |& "
puts "&| $side3 :|option switch mode, usually 1 for no decay, other modes = 2, 3, 4: | | |& "
puts "&| $side4 :|optional constant in other mode, nominal 1 :: | | |& "
puts "&| $side12 :| experimental constant_K1 : | | |& "
puts "&| $side1 :|dice sides number : | [optimum_N $side1] ] | $winner5 |& "
puts "&| $side5 :|probable 2 next throw : |[optimum_N $side1] |win at $winner5 |& "
puts "&| $side6 :|probable 3 next throw : |[optimum_N $side1] | win at $winner5 |& "
puts "&| $side7 :|probable 4 next throw : |[optimum_N $side1] |win at $winner5 |&"
puts "&| $side8 :|probable 5 next throw : | [optimum_N $side1] |win at $winner5|&"
puts "&| $side9 :|probable 6 next throw : | [optimum_N $side1] |win at $winner5|&"
puts "&| $side10 :|probable 7 next throw : | [optimum_N $side1] |win at $winner5|&"
puts "&| $side11 :|probable 8 next throw : | [optimum_N $side1] |win at $winner5|&"
}
frame .buttons -bg aquamarine4
::ttk::button .calculator -text "Solve" -command { calculate }
::ttk::button .test2 -text "Testcase1" -command {clearx;fillup 6.0 2024. 1. 1. 6. 6. 6. 6. 6. }
::ttk::button .test3 -text "Testcase2" -command {clearx;fillup 6.0 2024.2 1. 1. 6. 6. 6. 6. 6. }
::ttk::button .test4 -text "Testcase3" -command {clearx;fillup 20.0 2024.5 1. 1. 6. 6. 6. 6. 6.}
::ttk::button .clearallx -text clear -command {clearx }
::ttk::button .about -text about -command {about}
::ttk::button .self_help -text self_help -command {self_help }
::ttk::button .cons -text report -command { reportx }
::ttk::button .exit -text exit -command {exit}
pack .calculator -in .buttons -side top -padx 10 -pady 5
pack .clearallx .cons .self_help .about .exit .test4 .test3 .test2 -side bottom -in .buttons
grid .frame .buttons -sticky ns -pady {0 10}
. configure -background aquamarine4 -highlightcolor brown -relief raised -border 30
wm title . "Dragon Counting Dice Game V2 "
# end of working deck
# add cosmetics below to bottom of file
console eval {.console config -bg palegreen}
console eval {.console config -font {fixed 20 bold}}
console eval {wm geometry . 40x20}
console eval {wm title . " Report for Dragon Counting Calculator V2 "}
console eval {. configure -background orange -highlightcolor brown -relief raised -border 30}
puts " Console wrapper for solution proc"
puts " ***************************"
puts " ***************************" appendix : Script on Tables for TCL console
proc winnerx {aa bb} {
global sumit sumitland
#puts "end of game"
#.t insert 1.0 "end of game"
if { $sumit >= 500 } {
puts "winner declared"
}
if { $sumitland >= 500 } {
puts "winner declared"
}
}
appendix, counting through a list of thrown dice combos for probability
gold Here's counting through a list of thrown dice combos for probability. The worker bee is lsearch -all $lister $facen $facen is the sum of a 2-dice throw like 7. Subroutine is invoked by a foreach procedure for probability, which would be number of thrown 7's over all possible throws ($lister). Drop (-all) and lose all, returning only one position of "7" in list. See Binomial Probability Slot Calculator Example.
Other dice and random examples on Wiki. The random pick algorithm was posted by Suchenworth RS on Horseracing in Tcl. Using the random pick algorithm from Suchenworth RS is an alternate way to simulate dice play and sometimes easier for the non standard dice set ups. Other dice pages are Throwing Two Dice GWM and Dice by Keith Vetter. Also int from RLE has dice expression expr {1 + int(rand()*6)} RLE. Several Dr. Math emails may reduce some dice issues to simple paths.
console show
proc calculation { facen } {
# prob. subroutines for two 6-sided dice
set lister {2 3 4 5 6 7 3 4 5 6 7 8 4 5 6 /
7 8 9 5 6 7 8 9 10 6 7 8 9 10 11 7 8 9 10 11 12}
set ee [llength $lister ]
set kk [ llength [ lsearch -all $lister $facen ] ]
set prob [ expr { ($kk*1.) / $ee } ]
return $prob
}
set limit 12
for { set i 1 } { $i <= $limit } { incr i } {
lappend listxxx $i
lappend listxxx [ calculation $i ]
puts " $i [ calculation $i ] "
}
#end Appendix Subroutine for table in TCL Wiki Format
Adapted proc from RS
proc table_format_out n {
set sum 0
# initial level
set count 0.0
set glucose 100.
puts "%| table| | printed in|TCL format |% "
puts "%| homa_IR_2 units | insulin units |glucose units |comment, if any|% "
# adapted proc from <RS>
# printout in TCL WIKI format table
for { set i 1 } { $i <= $n } { incr i } {
set count [+ $count .1]
set insulin $count
set homa_IR_2 [ HOMA_IR2 $insulin $glucose ]
set insulin [ precisionx 3 $insulin ]
set glocose [ precisionx 3 $glucose ]
puts "&| [ precisionx 3 $homa_IR_2 ] | $insulin | $glucose | |&"
incr sum $i
}
return $sum
}
table_format_out 90 Console program for quantity_into_ratios
# pretty print from autoindent and ased editor
# quantity_into_ratios for math::stats? package
# working under TCL version 8.5.6 and eTCL 1.0.1
# console program written on Windows XP on eTCL
# gold on TCL WIKI, 2Mar2017
package require Tk
console show
package require math::numtheory
namespace path {::tcl::mathop ::tcl::mathfunc math::numtheory }
set tcl_precision 17
# adapted from tcl-wiki Stats 2011-05-22, arithmetic mean [RLE]
#
# ::math::quantity_into_ratios --
#
# Return the division of quantity by two or more given ratios
#
# Arguments:
# val first value is quantity
# args other values are two or more given ratios
#
# Results: parts of quantity divided by ratios
#
proc ::math::quantity_into_ratios {quantity args} {
set sum 0.
set N [ expr { [ llength $args ] + 1 } ]
if { $N == 1 } { return 0 }
foreach val $args {
set sum [ expr { $sum + $val } ]
}
foreach val $args {
lappend answer [ expr { $quantity * ($val/$sum) } ]
}
set answer
}
puts " ::math::quantity_into_ratios ( 84 2 2 2 ) answer 12.0 24.0 48.0 "
puts " [ ::math::quantity_into_ratios 84 1 2 4 ] "
puts " [ ::math::quantity_into_ratios 84 ] for (::math::quantity_into_ratios 84) returns zero "
#end of deckConsole program for geometric_mean
# pretty print from autoindent and ased editor
# geometric_mean for math::stats? package
# working under TCL version 8.5.6 and eTCL 1.0.1
# console program written on Windows XP on eTCL
# gold on TCL WIKI, 2Mar2017
package require Tk
console show
package require math::numtheory
namespace path {::tcl::mathop ::tcl::mathfunc math::numtheory }
set tcl_precision 17
# adapted from tcl-wiki Stats 2011-05-22, arithmetic mean [RLE]
console show
# ::math::geometric_mean --
#
# Return the geometric_mean of two or more values
#
# Arguments:
# val first value
# args other values
#
# Results:
# geometric_mean arithmetic geometric_mean value
proc ::math::geometric_mean { args } {
set product 1.
set N [ expr { [ llength $args ] } ]
foreach val $args {
set product [ expr { $product*$val } ]
}
set exponent [ expr { 1./$N } ]
set geometric_mean [ expr { $product**$exponent } ]
#puts " $N $exponent $product $args "
set geometric_mean
}
puts " ::math::geometric_mean ( 1 2 3 4 ) answer 2.2133638 "
puts " [ ::math::geometric_mean 1 2 3 4 ] answer 2.2133638 "
#end of deckAppendix on Stick Dice
Note on 13Feb2024.
2 yes-no binary sticks equals 2**2 combinations or 16 combinations. Probability of single cast 1/(2**2) or 1/4. Space = 4 items
4 yes-no binary sticks equals 2**4 combinations or 16 combinations. Probability of single cast 1/(2**4) or 1/16. Space = 16 items
5 yes-no binary sticks equals 2**5 combinations or 32 combinations. Probability of single cast 1/(2**5) or 1/32. Space = 32 items
6 yes-no binary sticks equals 2**6 combinations or 64 combinations. Probability of single cast 1/(2**6) or 1/64. Space = 64 items
7 yes-no binary sticks equals 2**7 combinations or 128 combinations. Probability of single cast 1/(2**7) or 1/128. Space = 128 items
Chinese excavations reveal a possible related divination system with space of 60 combinations.
There are current Buddhist temple methods that picking a stick from 64 sticks or some other number. Popular Game of Pick up Sticks in West. In that case, the classic formula would be 1/64 for equal Hexagram probability and the probability space would 64 items.
Bernoulli probability formula, P(Yang)= 1- P(Yin) The three most frequently occurring characters are: 吉 auspicious 无咎 no misfortune 凶 ominous Thinking in Bullet Points There are a total of 384 lines in the I Ching Oracle Book There are roughly 100 lines with character "mistake", Chinese "Liu" 100/384 = 0.2604 probability of mistake Liu appearing (384-100)= 284 number of lines without mistake Liu appearing 284/384= 0.7396 probability of mistake Liu not appearing The probability of casting a line with the character "mistake" is 0.2604, roughly 1/4 or 0.25 The probability of casting a line with no character "mistake" is 0.7396, roughly 3/4 or 0.75 The probability of casting a line with or without character "mistake" is 0.2604 + 0.7396 = 1 One might conclude the I Ching Oracle Book is rigged not to cast a character "mistake".
Appendix. Still Proof Reading Here
The probability space of hexagram diagrams generated by the cast of binary dice. While I don't have direct experience with this specific problem, I can provide some general guidance on how to approach this type of question.First, it's essential to clarify the problem statement and ensure that one have a clear understanding of the rules and constraints. In this case, one is considering dice marked with binary digits (0 or 1), and one want to calculate the probability space for the sum of the dice throws as they form the bars of a hexagram diagram.To solve this problem, one can use combinatorics and probability theory. one will need to determine the number of possible outcomes for each die throw and then calculate the probability of each outcome. This will help one to find the probability space for the hexagram diagrams. Here's a step-by-step approach to solving this problem:
Determine the number of sides on each die and the number of dice being cast. In this case, one have 6 dice, each with 2 sides (0 or 1).
Calculate the total number of possible outcomes for each die throw. Since each die has 2 sides, there are 2^6 = 64 possible outcomes for the 6 dice cast.
Determine the probability of each possible outcome. The probability of a single outcome is 1/(2^6), or 1/64.
Calculate the probability space for the hexagram diagrams by considering the sum of the dice throws. one can use combinatorics to determine the number of ways to achieve each possible sum and then multiply that number by the probability of each outcome.
Analyze the results and compare them to the Chinese diagnostics for the 64 diagrams, if applicable.
Regarding references for similar dice problems, it's likely that there is existing literature on combinatorics and probability theory that covers this type of problem. one may want to consult textbooks or research papers in these fields for more specific examples and solutions.
As for the distribution of 6 dice, it is indeed a binomial distribution. In a binomial distribution, there are a fixed number of trials (in this case, 6 dice throws), each with a binary outcome (success or failure). The probability of success for each trial is constant, and the trials are independent. In this problem, the probability of success (rolling a 1) is 0.5, and the probability of failure (rolling a 0) is also 0.5. The binomial distribution can be used to calculate the probability of observing a specific number of successes in the 6 dice throws. I hope this guidance helps one in research and analysis of hexagram diagrams and binary dice problems.
To create a probability plot for rolling three 4-sided dice with the given markings, we can follow these steps: Calculate the probability of each outcome by dividing the number of ways to achieve that outcome by the total number of possible outcomes (64).
Create a bar chart with the outcomes on the x-axis and their respective probabilities on the y-axis.
Label the x-axis with the outcomes and the y-axis with the probabilities.
Add a hexagram diagram with the sum of each cast as the base bar and the sum of the sixth dice throw as the top bar.
Check for accuracy? >>> Here's an example probability plot for rolling three 4-sided dice with the given markings, specifically for the 64 diagrams in the Chinese I Ching Oracle Book: Probability Plot for Rolling Three 4-Sided Dice with Given Markings Specific to the 64 Diagrams in the Chinese I Ching Oracle Book In this plot, the x-axis represents the possible outcomes (ranging from 1 to 16), and the y-axis represents the probability of each outcome. The bar chart shows the probability distribution, with the most likely outcomes being rolling a 10 or a 11 and the least likely outcomes being rolling a 1 or a 16. The hexagram diagram at the top represents the sum of each cast, with the base bar being the sum of the first dice throw and the top bar being the sum of the sixth dice throw.
Test Deck
Note. I did find a useful online IDE, https://www.jdoodle.com/execute-tcl-online/ . I can paste from local text file, edit, and run a test deck of TCL. I guess we should stop computing chain after so long, but kind of interested in looking at the trajectory of sum of random throws. One might wonder how one can win and lose at same time. "take the money and run" was the old saying. keep playing and empty wallet.
# Mock Up for Dragon Dice Deck V3
# pretty print from autoindent and ased editor
# throw N-sided dice until => chosen optimum number,
# declare winner or loser
# Dragon Counting Dice Game calculator
# written on Windows 10
# working under TCL version 8.6
# gold on TCL WIKI, 30jan2024
global sumit winner5 score side4
global loser5 goalpost scorecard
set winner5 0
set loser5 0
set sumit 1
set side4 1
proc dice_sides_N { dice_sides } { expr { 1 + int(rand()*$dice_sides)} }
proc optimum_N { dice_sides } { expr { int(1.718281828 *$dice_sides) }}
proc calculations_test {dummy_variable } {
# test dice casting section
global sumit winner5 score side4
global loser5 goalpost scorecard
set sumit 1
set side4 1
# not sure what cast number pops out
set side4 [ dice_sides_N 6 ]
set score $side4
set goalpost [ optimum_N 6 ]
# should be 10 for 6-sided die
winner_eval 5
}
proc winner_eval {dummy_variable} {
global sumit winner5 score side4
global loser5 goalpost scorecard
# winner5 and loser5 are global logic variables
# initialize winner5
# initialize loser5
set sumit 1
set winner5 0
set scorecard 0
set side4 5
set score 0
# goalpost calculates optimum [ optimum_N 6 }
set goalpost [ optimum_N 6 ]
set scorecard 0
# 1 2 3 4 5 6 7 8 9 10 11
foreach i { 4 5 6 7 8 9 10 11 12 } {
set side$i $i
set placeholder $i
set side$i $placeholder
puts " placeholder $placeholder "
set placeholder [ dice_sides_N 6 ]
puts " placeholder $placeholder die cast here "
set scorecard [ expr { $placeholder + $scorecard } ]
puts "sum casts for scorecard $scorecard ref goalpost $goalpost "
if { $scorecard < $goalpost} { puts "flagged less " }
if { $scorecard > $goalpost} { puts "flagged greater" }
if { $scorecard > $goalpost} { puts "loser declared"; set loser5 1 }
if { $scorecard == $goalpost} { puts "flagged equal and win" }
if { $scorecard == $goalpost} { puts "flagged equal winner declared" }
if { $scorecard == $goalpost} { set winner5 1 }
puts " goalpost $goalpost "
}
# 1 2 3 4 5 6 7 8 9 10 11
# set winner5 1
puts " winner5 $winner5 scorecard $scorecard goalpost $goalpost loser5 $loser5 "rare winner, most time fly past goalpost.
placeholder 4 placeholder 3 die cast here sum casts for scorecard 3 ref goalpost 10 flagged less goalpost 10 placeholder 5 placeholder 2 die cast here sum casts for scorecard 5 ref goalpost 10 flagged less goalpost 10 placeholder 6 placeholder 1 die cast here sum casts for scorecard 6 ref goalpost 10 flagged less goalpost 10 placeholder 7 placeholder 3 die cast here sum casts for scorecard 9 ref goalpost 10 flagged less goalpost 10 placeholder 8 placeholder 1 die cast here sum casts for scorecard 10 ref goalpost 10 flagged equal and win flagged equal winner declared goalpost 10 placeholder 9 placeholder 6 die cast here sum casts for scorecard 16 ref goalpost 10 flagged greater loser declared goalpost 10 placeholder 10 placeholder 1 die cast here sum casts for scorecard 17 ref goalpost 10 flagged greater loser declared goalpost 10 placeholder 11 placeholder 2 die cast here sum casts for scorecard 19 ref goalpost 10 flagged greater loser declared goalpost 10 placeholder 12 placeholder 3 die cast here sum casts for scorecard 22 ref goalpost 10 flagged greater loser declared goalpost 10 winner5 1 scorecard 22 goalpost 10 loser5 1
Test on pretty print
# Mock Up for Dragon Dice Deck V4
# pretty print from autoindent and ased editor
# throw N - sided dice until => chosen optimum number,
# declare winner or loser
# Dragon Counting Dice Game calculator
# written on Windows 10
# working under TCL version 8.6
# gold on TCL WIKI, 30 jan2024
global sumit winner5 score side4
global loser5 goalpost scorecard
set winner5 0
set loser5 0
set sumit 1
set side4 1
proc dice_sides_N {
dice_sides
} {
expr {
1 + int(rand() * $dice_sides)
}
}
proc optimum_N {
dice_sides
} {
expr {
int(1.718281828 * $dice_sides)
}
}
proc calculations_test {
dummy_variable
} {
# test dice casting section
global sumit winner5 score side4
global loser5 goalpost scorecard
set sumit 1
set side4 1
# not sure what cast number pops out
set side4[dice_sides_N 6]
set score $side4
set goalpost[optimum_N 6]
# should be 10
for 6 - sided die
winner_eval 5
}
proc winner_eval {
dummy_variable
} {
global sumit winner5 score side4
global loser5 goalpost scorecard
# winner5 and loser5 are global logic variables
# initialize winner5
# initialize loser5
set sumit 1
set winner5 0
set scorecard 0
set side4 5
set score 0
# goalpost calculates optimum[optimum_N 6
}
set goalpost [optimum_N 6]
set scorecard 0
# 1 2 3 4 5 6 7 8 9 10 11
foreach i {
4 5 6 7 8 9 10 11 12
} {
set side$i $i
set placeholder $i
set side$i $placeholder
puts " placeholder $placeholder "
set placeholder [dice_sides_N 6]
puts " placeholder $placeholder die cast here "
set scorecard [expr {
$placeholder + $scorecard
}]
puts "sum casts for scorecard $scorecard ref goalpost $goalpost "
if {
$scorecard < $goalpost
} {
puts "flagged less "
}
if {
$scorecard > $goalpost
} {
puts "flagged greater"
}
if {
$scorecard > $goalpost
} {
puts "loser declared";
set loser5 1
}
if {
$scorecard == $goalpost
} {
puts "flagged equal and win"
}
if {
$scorecard == $goalpost
} {
puts "flagged equal winner declared"
}
if {
$scorecard == $goalpost
} {
set winner5 1
}
puts " goalpost $goalpost "
}
# 1 2 3 4 5 6 7 8 9 10 11
# set winner5 1
puts " winner5 $winner5 scorecard $scorecard goalpost $goalpost loser5 $loser5 "One Liner Programs & Simple One Liner Procedure
These one liner procedures demonstrate the simplicity and conciseness of TCL programming, while still being able to perform useful tasks.
Appendix: Test on Pretty Print
This program, called "math::quantity_into_ratios," takes a quantity and a list of ratios as arguments and returns the parts of the quantity divided by the ratios.
package require Tk
console show
package require math::numtheory
namespace path {::tcl::mathop ::tcl::mathfunc math::numtheory }
set tcl_precision 17
proc ::math::quantity_into_ratios {quantity args} {
set sum 0.
set N [ expr { [ llength $args ] + 1 } ]
if { $N == 1 } { return 0 }
foreach val $args {
set sum [ expr { $sum + $val } ]
}
foreach val $args {
lappend answer [ expr { $quantity * ($val/$sum) } ]
}
set answer
}Efficiency of the TCL code
Comments Section
Please place any comments here with your wiki MONIKER and dates, Thanks,gold 24FEB2024
under test
gold 2/20/2024. This a big file. Check earlier editions, if not compatible. Maybe obvious and stated in TCL deck, but this page was written on Windows10 Tcl ports including ActiveTCL. I assume that the reader can cut and paste on screen, what the reader needs, and tootle on to his own bio-project and own contribution pages to the TCL Wiki. The author is retired engineer and no longer has { proofing access } to Unix machines. Unix is respected after use of so many years in engineering, but my wings are lost.
gold 2024-02-20. These calculator approaches in TCL console guis for Windows10 may seem trivial math to some, but I have submitted 4 or 5 TCLLIB tickets to improve the TCLLIB math library. For example, the math and logic functions IsOdd, IsEven, IsNegative, IsPositive, figurative_numbers, and Quadratic_Equation_Solution_for_reals were not in the TCLLIB library, as near as I can tell. Maybe these logic functions on integers and Quadratic_Equations_Solutions on reals are trivial math to some, but these Quadratic_Equations_Solutions and other math functions show up in some other math languages, TCL programs, and even TCL WIKI pages. As HE implies, the main idea of TCL or other computer language is that other users can share the faster compiled code rather than homebrew functions. Since I am retired and I do not have easy access to a UNIX machine, the only course in the USA retirement economy is to proof and study the TCL routines on a Windows10 PC.
the probability plot of rolling a 20-sided dice. In the context of a probability plot, we are looking for the probability of each outcome (rolling a 1, 2, 3, ..., 20) and how they are distributed. Since a fair 20-sided dice is equally likely to land on any of its sides, the probability of rolling each number is the same. For a fair 20-sided dice: The probability of rolling a 1, 2, 3, ..., or 20 is 1/20 or approximately 0.05 A probability plot for a fair 20-sided dice would show a uniform distribution, with each number having an equal probability of being rolled.
The probability plot of rolling three 6-sided dice. In the context of a probability plot, we are looking for the probability of each outcome (rolling a 3, 4, 5, ..., 18) and how they are distributed. When rolling three 6-sided dice, the total number of possible outcomes is 6 * 6 * 6 = 216. The probability of each outcome is calculated by dividing the number of ways to achieve that outcome by the total number of possible outcomes (216). For example, there is only one way to roll a 3 (rolling a 1 on all three dice) and one way to roll an 18 (rolling a 6 on all three dice), so the probability of rolling a 3 or an 18 is 1/216 or approximately 0.00463. Here is the probability distribution for rolling three 6-sided dice:
Probability of rolling a 3: 1/216 or approximately 0.00463 Probability of rolling a 4: 3/216 or approximately 0.0139 Probability of rolling a 5: 6/216 or approximately 0.0278 Probability of rolling a 6: 10/216 or approximately 0.0463 Probability of rolling a 7: 15/216 or approximately 0.0694 Probability of rolling a 8: 21/216 or approximately 0.0977 Probability of rolling a 9: 25/216 or approximately 0.1164 Probability of rolling a 10: 27/216 or approximately 0.1250 Probability of rolling a 11: 27/216 or approximately 0.1250 Probability of rolling a 12: 25/216 or approximately 0.1164 Probability of rolling a 13: 21/216 or approximately 0.0977 Probability of rolling a 14: 15/216 or approximately 0.0694 Probability of rolling a 15: 10/216 or approximately 0.0463 Probability of rolling a 16: 6/216 or approximately 0.0278 Probability of rolling a 17: 3/216 or approximately 0.0139 Probability of rolling a 18: 1/216 or approximately 0.00463
A probability plot for rolling three 6-sided dice would show a bell-shaped distribution, with the most likely outcomes being rolling a 10 or a 11 and the least likely outcomes being rolling a 3 or an 18.
To improve the TCL code, you can follow these suggestions: Use meaningful variable names: Instead of using single letter variable names like 'i', 'msg', and 'proc', use more descriptive names that help convey the purpose of the variable. This will make the code more readable and easier to understand. Break down complex procedures into smaller functions: The current code has a single procedure called 'calculate' which performs multiple tasks. It would be better to break down this procedure into smaller, more manageable functions that perform specific tasks. This will make the code easier to maintain and debug. Use comments to explain the code: Adding comments to explain what each section of code does can greatly improve the readability and maintainability of the code. Use comments to explain the purpose of the code, any assumptions made, and any caveats or limitations. Use consistent indentation and formatting: Ensure that the code is consistently indented and formatted. This will make it easier to read and understand the flow of the code. Use a consistent style guide for indentation, spacing, and line breaks. Use meaningful error handling: Add error handling to the code to handle unexpected inputs or situations. Use descriptive error messages to help users understand what went wrong and how to fix it. Use version control: Use a version control system like Git to keep track of changes to the code. This will make it easier to collaborate on the code and to roll back to previous versions if necessary. By following these suggestions, you can improve the readability, maintainability, and functionality of the TCL code..