Dragon Counting Dice Game V4 , dice procedure algorithm and TCL 8.6 demo example calculator, numerical analysis
This page is under development. Comments are welcome, but please load any comments in the comments section at the bottom of the page. Please include your wiki MONIKER and date in your comment with the same courtesy that I will give you. Aside from your courtesy, your wiki MONIKER and date as a signature and minimal good faith of any internet post are the rules of this TCL-WIKI. Its very hard to reply reasonably without some background of the correspondent on his WIKI bio page. Thanks,gold 20FEB2024
- Title: Dragon Counting Dice Game V4
- Preface
- Not a Replacement for TCL Core
- Introduction
- Features of Dragon Counting Dice Game
- Body
- Test Deck for Dice
- TCL is a powerful and versatile computer language
- Start with a working TCL math template or TCL math subroutine to modify it
- Comparison of the Algorithm(s)
- Stick Dice
- Push Button Operation
- Procedures and subroutines
- Main code description
- Conclusions
- Table 1: Table for 6 sided single die mass probability function
- Table 2: Table for two 6-sided dice, mass probability function
- Table 3: Table for two 2-sided dice, mass probability function
- Table 4: Table for two 20-sided dice, section of mass probability function
- Table 5: List of casts on dice 64
- Testcases Section
- Screenshots Section
- figure 1a. Dragon Counting Dice Game V2 vaporware screenshot
- figure 1t. Dragon Counting Dice Game V4, second vaporware screenshot
- figure 1r. Dragon Counting Dice Game V4, various flowcharts
- figure 1z. Dragon Counting Dice Game V4, output display for tables in TCL Wiki format
- figure 1c. Dragon Counting Dice Game 20 sides2
- figure 2. Chinese Numbers
- figure 3. Favorite camera on child, commercial game
- figure 4. from Wikipedia, Snakes and Ladders probability after N Turns, commercial game
- figure 5. from Wikipedia, Dragon Counting Dice Game V2 child snake ladder chase game jain
- figure 6 . from Wikipedia, Dragon Counting Dice Game V2 child snake ladder chase game illustration
- figure 7 . replicas , Dragon Counting Dice Game V2 6 sided single die mass probability function
- figure 8 . from Wikipedia, Dragon Counting Dice Game V3 two 6-sided dice mass probability function
- figure 9 . from Wikipedia, Dragon Counting Dice Game V3 6 2-sided stick dice for 64 space
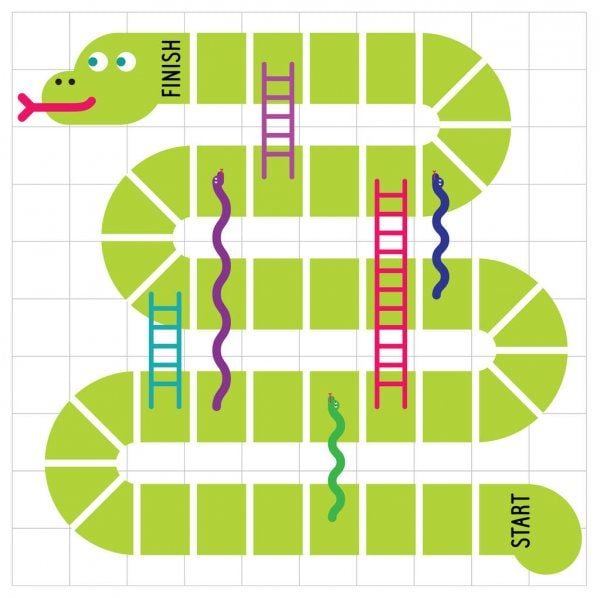
- figure 10 . from Wikipedia, Dragon Counting Dice Game V3 child snake ladder chase game board
- figure 11. Stick Dice
- figure 12. Chinese Abacus
- figure 13. Replica Sundial with Hexagram Marks
- figure 14. Stick Dice
- Screenshots Section
- References:
- Pseudocode & Equations Section
- Appendix Code
- Trial Calculator Shell , Mock Up for Dragon Dice Deck V4
- Error reconstruction on data type in List
- appendix : Script on Tables for TCL console
- appendix, counting through a list of thrown dice combos for probability
- Appendix on Stick Dice
- Appendix. Still Proof Reading Here
- Appendix: Test on Pretty Print
- Comments Section
Title: Dragon Counting Dice Game V4
Preface
gold 2/20/2024 Update. Here are some TCL scripts on the Dragon Counting Dice Game. I found some references on probability for the Snake and Ladder game. Separate console programs were developed to dump the tables and check the algorithms as independent TCL procedures. These auxiliary decks are used to proof features or subroutines of the prospective gui program. The Monopoly page from GWM seems closest in theme to what I was trying to learn. Using dice and running with random throws along a track or path like Snakes and Ladders. Received useful and constructive feedback from offsite, thanks to @Ava______. Some text rephrasing to apply as general advice to most TCL programs.
The author is retired engineer on Windows 11 and no longer has { proofing access } to Unix machines. Unix is respected after use of so many years in engineering, but my wings are lost. The impetus for this calculator was checking some probabilities on the Dragon Counting Dice Game. It is easy enough to plug in formulas/subroutines into the display formats. Most of the checked testcases involve flipping two sided objects like coins ,popsicle sticks, regular box dice, or four sided rectangular dice. This page is more an investigation into the mindset of the Chinese sages, using TCL visual and random subroutines.
Not a Replacement for TCL Core
This page on developing pseudocode examples and one line procedures is not a replacement for the current Tcl core and Tcllib, which is much improved since Tcl version 4, and other <faster> language constructs. math ops, Tcllib routines, and other compiled routines can reduce the cost of big-data tasks by about 1/3. The time savings of the core are not always obvious on small quantities of data, like 4 or 5 numbers. Performance of one-line programs may suffer degradation due to lengthy recursion calls, and may be limited by constraints on recursion. Dependence on math operator notation, helper procedures, math check examples, degradation due to lengthy recursion calls, and special library functions should be noted in the comment lines.
Introduction
One is trapped in a dungeon with a 20-sided die, and a dragon demands that one pick a specific "sweet integer" number and roll a specific total to escape. For example, one choose the number 42, and if one succeed, one can leave the dungeon. If one fails to land on the optimum number, one will be stuck with the dragon or face the dragon penalty box.
Gist. In the cited scenario for the Dragon Counting Dice Game, one must choose a "sweet number" to roll on a 20-sided die to escape. The concept of a "sweet number" in this context refers to an integer that, when rolled on the die, results in oner escape from the dungeon. To optimize one's chances, one may use mathematical approximations involving natural logarithms and large numbers to guide oner selection of the sweet number. One such approximation involves multiplying the chosen number by a specific constant to determine the optimum choice. Ultimately, the goal is to select a number that increases one's likelihood of success in escaping from the dungeon and avoiding the dragon's penalty box.
There is also possibility of a trial and error algorithm. Meaning play the game enough times, advancing a guess from trial and error might be a possible strategy.
Features of Dragon Counting Dice Game
This TCL program as a game uses a random number generator and the specified number of sides on a die. Then the game rolls the die a specified number of times. At the start of the game, the user gives either a guess or estimate from natural logarithm "e" for the optimal score. The program determines whether the total score from the rolls is less than, equal to, or greater than an optimal score. The optimal score is calculated using the formula int(1.718281828 * $dice_sides ). The program keeps track of the casts and tallies of each roll, as well as the winner and loser status.
The rule of thumb for finding the maximum of a function involving natural logarithms and large values of N is to multiply N by a certain approximation. "Sweet winning number" as optimum number in dragon counting game is reported between N and 2N. As rule of thumb, a mathematician James Munro reported that Sweet Number rule as rounded {(e-1)*N)}. However, 1 plus phi conjugate or rounded {(1.6180339887 * N)} would give equivalent answer in small number field, less than 10. Correction here: the optimal number for the original 20-sided die problem is actually ~35. This is slightly better than the first quibble guess of 42. Mathematician has been fed to the dragon as punishment for this dragonish error. Not sure what significance that a "sweet number" means to the dragon. Maybe all numbers are sweet to the dragon at meal time , short of infinity.
Under Math Check & Review, something may not be accurate? :::: The rule of thumb for finding the maximum of a function involving natural logarithms and large values of N is to multiply N by a certain approximation. This approximation is often used when dealing with functions that have a similar shape to the natural logarithm function. By multiplying N by the approximation, you can get a close estimate of the maximum of the function. This rule of thumb is particularly useful when working with large numbers, as it can save time and computational resources compared to finding the exact maximum. The specific approximation used can vary depending on the context and the function being analyzed. But the specific approximation or optimum generally involves multiplying N by a number expression using 2.718281828, which is the mathematical constant known as Euler's number. To find the maximum of a function involving natural logarithms and large values of N, you can use the approximation method. This involves multiplying N by a certain approximation factor. For example, let's consider the function f(N) = N * ln(N). To find the maximum of this function, you can use the approximation N * ln(N) ≈ (N+1) * ln((N+1)/e), where e is the base of the natural logarithm (approximately 2.71828). By applying this approximation, you can find the maximum value of N that makes the function reach its maximum.
Note. This optimization function is sometimes called expm1(x) = exp(x) − 1.
Evaled at 1, general expression is expm1(x) = exp(x) − 1., exp(1) − 1. = 1.718281828
Body
Under Math Check & Review, something may not be accurate? :::: A Snakes and Ladders Chase game is a variation of the classic board game Snakes and Ladders. In this version, two players or teams race to reach the finish line while trying to avoid getting sent back by the snakes and climb up the ladders. The game can be played on a standard Snakes and Ladders board or by using a customized board with additional rules. To play, each player or team takes turns rolling the dice and moving their game piece along the board according to the number rolled. If a player lands on a ladder, they can move up to the higher square indicated by the ladder. However, if they land on a snake's head, they must move down to the corresponding tail square. The first player to reach the finish line (usually the last square on the board) wins the game. This version of the game adds a competitive and strategic element, as players try to outmaneuver each other while navigating the snakes and ladders. It can be a fun and engaging way to introduce children to basic strategy and probability concepts while enjoying a classic board game.
By engaging in games like Snakes and Ladders Chase, children can learn to think strategically, analyze patterns, and develop their understanding of probability. These skills can be applied to various fields, including science and technology, and can help to prepare young minds for the challenges of the modern world. I hope that games like Snakes and Ladders Chase continue to be enjoyed by children and adults alike, as they provide not only entertainment but also valuable opportunities for learning and personal growth.
Under Math Check & Review, something may not be accurate? :::: The optimization function expm1(x) or exp(x) - 1 is used in numerical analysis, particularly in scientific and engineering applications, where it serves as an alternative to the standard exponential function exp(x). The expm1(x) function computes the value of e^x - 1, which is the difference between the exponential function and 1. This function is particularly useful in situations where the values of x are small, as it provides a more accurate result than the standard exp(x) function in such cases. The exp(x) - 1 function is essentially an approximation of expm1(x), and is used in situations where the precision of expm1(x) is not required, or when the function is not available in a particular programming language or library. Both functions have their specific use cases, and the choice between them depends on the accuracy requirements and the programming environment being used.
Check. The ability to compute the difference between the exponential function and 1 with greater precision when dealing with small values of x can be particularly valuable in situations where even slight inaccuracies can have significant consequences.
The canvas and buttons presented here are largely based on the Simple Canvas Demo by HJG. The random pick algorithm was posted by Suchenworth RS on Horseracing in Tcl. Using the random pick algorithm from Suchenworth RS is an alternate way to simulate dice play and sometimes easier for the non standard dice set ups. Other dice pages are Throwing Two Dice GWM and Dice by Keith Vetter. Also int from RLE has dice expression expr {1 + int(rand()*6)} RLE. Several Dr. Math emails may reduce some dice issues to simple paths. another useful wiki page was Counting Elements in a List from RWT.
The units can be changed in the internal calculator formulas as TCL code. Any convenient and consistent output units might be used like millimeters, inches, cubits, feet, or dollars to donuts.
Test Deck for Dice
I did find a useful online IDE, jdoodle. I can paste from local text file, edit, and run a test deck of TCL. I guess we should stop computing chain and endless loop after so long, but kind of interested in looking at the trajectory of sum of random throws. I guess there are lower bounds and upper bounds in the sum of dice throws. Planned to offer section of dice sides, other than one 20-sided die. One might wonder how one can win and lose at same time. "take the money and run" was the old saying, keep playing longer and empty wallet.
gold 2/20/2024 update. A console program has been modified to check the results and timing of one liner procedures in the script. The user can add new algorithms by adding a new one liners program in the source code. One may add a number line to the if statement that controls the algorithm selection in the console program. The one liner procedures and solutions can also be pasted into the TCL console easily. The accuracy of these individual solutions varies with the number of trials and some algorithms used are fairly slow, even glacial closers. Most of the one liners programs and usage examples should be pastable into the TCL console.
TCL is a powerful and versatile computer language
gold Update 2/29/2024. Received useful and constructive feedback from offsite, thanks to @Ava______. Some text rephrasing to apply as general advice to most TCL programs.
Under Math Check & Review, something may not be accurate? :::: Tool Control Language (TCL) is a programming language used in automation, especially in industrial automation and manufacturing. It is designed to control various tools, machines, and processes, allowing for precise and efficient execution of tasks. TCL is based on the IEC 61131 standard, which is an international standard for programming languages used in industrial automation. It is a high-level, text-based language that provides a clear and concise way to describe actions and sequences, making it easier for automation engineers to develop and maintain control programs. TCL can be used to program a wide range of devices and systems, including PLCs (Programmable Logic Controllers), robots, CNC machines, and other industrial equipment. By using TCL, manufacturers can optimize their production processes, reduce human error, and improve overall efficiency and productivity. Some key features of TCL include:
1. Structured programming: TCL supports structured programming concepts, such as IF-THEN-ELSE statements, FOR, Foreach, and WHILE loops, and functions, which enable the creation of modular and reusable code.
2. Data types: TCL supports various data types, including integers, floats, strings, and arrays, allowing for the manipulation and storage of different types of data.
3. Input/Output operations: TCL provides functions for reading and writing data from/to various sources, such as sensors, actuators, and data storage devices.
4. Timers and counters: TCL includes functions for creating timers and counters, which can be used to control the timing of actions and sequences.
5. User-defined functions: TCL allows users to create their own functions, which can be used to encapsulate and reuse common code sequences.
Overall, TCL is a powerful and versatile language for controlling industrial tools and processes, making it an essential tool for automation engineers and manufacturers.
Start with a working TCL math template or TCL math subroutine to modify it
gold 2/29/2024. Received useful and constructive feedback from offsite, thanks to @Ava______. Some text rephrasing to apply as general advice to most TCL programs.
To start with a working TCL math template from TCCLIB and modify it for a new purpose, follow these 6 steps:
1. Choose a TCL math template or TCL math subroutine, for example in the TCLLIB library: Find a suitable TCL math template that closely matches the functionality you want to achieve. You can find various templates online or in TCL programming books and resources.
2. Understand the template: Carefully read and understand the template's code, comments, and structure. This will help you identify the parts of the code that you need to modify to create your new purpose.
3. Identify the necessary modifications: Determine the specific changes you need to make to the template to achieve your desired functionality. This may include modifying input parameters, changing calculations, or altering the output format.
4. Modify the template code: Begin modifying the template code, following the guidelines provided by the TCL programming language. Make sure to update any comments or documentation to reflect the new purpose of the subroutine.
5. Test the new TCL subroutine: After making the necessary modifications, test the new TCL subroutine in a console program to ensure it functions as expected. This will help you identify and fix any errors or issues before integrating the subroutine into a graphical user interface (GUI).
6. Load the new TCL subroutine into a GUI: Once the new TCL subroutine has been tested and verified, you can load it into a GUI program that supports TCL scripting. Make sure to follow the GUI's documentation and guidelines for integrating TCL subroutines.
By following these steps, you can successfully start with a working TCL math template, modify it for a new purpose, and then load the new subroutine into a GUI program for further use.
Comparison of the Algorithm(s)
To make a chicken, it is said that God starts with nothing and makes a chicken, 0 --> 1. To make a chicken, man starts with two chickens and the two chickens make a chicken, 2 --> 3.
For global logic flags, the effect is cosmetic, but the flags keep confusion and gritty details out of the final accounting statements. Once the flags are set global, the flags can be reported and evaluated at all subsequent points in the subroutine. The flags can even be sent outside the subroutine with possible global statements as, global loss_this_year. In executive decisions, potential loss must be a factor.
Under Math Check & Review, something may not be accurate? :::: The approximation N * ln(N) ≈ (N+1) * ln((N+1)/e) is a well-known result in mathematics, where e is the base of the natural logarithm. It is often used in number theory and analysis. The golden ratio, on the other hand, is a mathematical concept that is found in nature and art. It is often denoted by the Greek letter phi (φ), and can be calculated as (1 + √5) / 2 ≈ 1.6180339887. It has many interesting properties, and is often used in art and design to create aesthetically pleasing compositions. expm1(x) is a mathematical function that is used to calculate the exponential of a number minus 1. It is often used in numerical analysis and scientific computing. The formula 1 plus phi conjugate {(1.6180339887 * N)} is a way of rounding a number to the nearest multiple of the golden ratio. It is often used in geometry and design, and can be used to create patterns and shapes that are pleasing to the eye.
Under Math Check & Review, something may not be accurate? :::: A single six-sided die has six equally likely outcomes, each with a probability of 1/6. The probability function for a single dice roll is: P(x) = 1/6, for x = 1, 2, 3, 4, 5, 6 This means that the probability of rolling any specific number (1 through 6) on a single dice roll is 1/6, or approximately 16.67%. A double six-sided die has 36 equally likely outcomes, each with a probability of 1/36. The outcomes are determined by the sum of the two dice rolls, ranging from 2 (both dice showing 1) to 12 (both dice showing 6). The probability function for a double dice roll is: P(x) = 1/36, for x = 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 This means that the probability of rolling any specific sum (2 through 12) on a double dice roll is 1/36, or approximately 2.78%.
Under Math Check & Review, something may not be accurate? :::: I am not sure how to define winning at dice games. It is said that some game players need to win one out of three games to keep interest up. Seems to be a common strategy in planning dice games, but it's not a hard rule or requirement for all games. It's based on the idea that players need to win occasionally to maintain their interest and enthusiasm in the game. In many dice games, winning one out of three games can be a good guideline to keep the game balanced and enjoyable for all players. However, this can vary depending on the specific game, the players' preferences, and the dynamics of the game. Some games might require more frequent wins to keep players engaged, while others might allow for longer streaks of losses without losing interest. Ultimately, it's up to the players to decide the frequency and conditions of winning that best suit their preferences and the game they're playing.
Stick Dice
The Iching is the ancient fortune telling book of China. The Iching literature mentions various methods for casting fortune patterns of Iching. The various methods include hot ironing of turtle shells (-t.), manipulations of yarrow sticks, flipping coins, throwing shaman bones, and dice. One analogy from North America is a shaman throwing or shuffling stick dice.
I made three stick dice for Iching by cutting a dowel of square cross section into three sticks. For the three stick dice, the flat sides are marked or burned with 2 or 3 holes alternately. Two sticks are marked with {3 2 3 2} dots on the sides. One stick is marked with {3 3 3 2} dots on the sides. In casting such three dice, the possible sums are 6,7,8, or 9. Further, the stick dice are cast six times to obtain whole lines or broken lines in a pattern or set of six lines. A set of six Iching lines is called a gua in the orient or a hexagram in some translations of the Chinese.
In the Iching interpretations, casts of 6 and 8 are broken or yin (female) lines, while casts of 7 and 9 are whole or yang (male) lines. The casts are recorded by pencil with the first line at bottom and marking up the column. It is possible to record the numbers from the casts with tally sticks or Chinese counting rods, which are somewhat reminiscent of the Iching patterns themselves. After marking the original pattern or hexagram, sometimes a second follow-up hexagram is developed by swapping throws of 6 for a 7 and throws of 9 for a 6. These swaps effectively trade a broken line(6) for a whole line(7) and a whole line(9) for a broken line(6). The throws for the changing lines (6&9) may not always be come out in the first hexagram or its component lines, so the followup hexagram may not exist {under consistent rules}. If the first hexagram is interpreted on a line by line basis, any changing lines(6&9) or second hexagram offers some modification or discount on the interpretation of the first hexagram.
In developing a computer program or application, it is helpful to develop analogs for the individual tasks of the application. An Iching application would have to compose, beg, or borrow TCL procedures for random casts, tallies of scores, accounting files, display hexagram lines on a screen, swapping changing lines, hexagram pattern recognition and ranking interpretations. In fact, some TCL one liner procedures and text swapping routines might be useful as utilities in a starter application program, since unruly text strings are expected in the Iching. Casting the sticks or bones for each Iching line is analog for random lpick subroutine below. Adding the top sides of three sticks and throwing six times is analog for the "for 6 times" statement in the bonereadxx procedure below. In the West, Leibniz etc recognized that the whole and broken lines in the hexagram patterns could be counted as ones and zeros, respectively in a binary number system. For example, a cast or TCL list of { 6,7,8,9,6,7 } could be expressed as a binary number, 010101. The binary numbers are the analogs for the binaryexchange subroutine below. For computer procedures, the patterns are effectively a horizontal bar code of 6 lines.
In the process of designing the basic subroutine tasks, we could throw in some switches, logic chains, or daisy chains that break the outset rules given above. For example, TCL is so good at swapping lines (6&9) for the second hexagram, that it would be easy to put a switch that generates or swaps all hexagram lines (6,7,8,&9) for their opposites. Also from some scripts of the Chinese Chou dynasty, different Iching fortune methods of yarrow sticks or coins would generate different probabilities of obtaining each hexagram line. Might be interesting to have a back door in the program to check (or adapt} the different probabilities of stick or coin throws.
Under Math Check & Review, something may not be accurate? :::: The probability of rolling a specific hexagram, which is a combination of six trigrams, on the Yi Jing, also known as the I Ching, is 1/64. This is because each trigram has 8 possible outcomes (4 broken lines and 4 solid lines), and when you roll two dice, you have 64 possible outcomes (8 x 8 = 64). To roll a specific hexagram, you need both dice to land on the specific trigrams you want, which is 1/64. >>>> I understand your point.<<<<< Probability theory is indeed based on the assumption that events are random, and it provides a framework for predicting the likelihood of different outcomes. If those phenomena are non-random, then the concept of probability and random outcomes may not apply. In the context of the Yi Jing or I Ching, the focus is often on exploring the possible outcomes and gaining insights from the results, rather than calculating mere probabilities. The purpose of these Yi Jing or I Ching practices is to provide guidance or understanding, rather than predicting random events.
Push Button Operation
For the push buttons, the recommended procedure is push a testcase and fill frame, change first three entries etc, push solve, and then push report. Report allows copy and paste from console. For testcases in a computer session, the TCL calculator increments a new testcase number internally, eg. TC(1), TC(2)., TC(3), TC(4) etc. The testcase number is internal to the calculator and will not be printed until the report button is pushed for the current result numbers. The current result numbers will be cleared on the next solve button. For comparison of the Babylonian algorithm with conventional Western methods, TCL code will include redundant procs, redundant calculation paths, and printout check formulas to compute product and area.
For testcases in a computer session, the TCL calculator increments a new testcase number internally, eg. TC(1), TC(2) , TC(3) , TC(N). The testcase number is internal to the calculator and will not be printed until the report button is pushed for the current result numbers. The current result numbers will be cleared on the next solve button. The command { calculate; reportx } or { calculate ; reportx; clearx } can be added or changed to report automatically. Another wrinkle would be to print out the current text, delimiters, and numbers in a TCL wiki style table as
puts " %| testcase $testcase_number | value| units |comment |%" puts " &| volume| $volume| cubic meters |based on length $side1 and width $side2 |&"
Procedures and subroutines
1. About: Displays information about the calculator, such as version number and author.
2. Self_help: Provides a brief guide on how to use the calculator, including input formats and recommended procedures.
3. Dice_sides_N: Generates a random number between 1 and the given dice_sides value.
4. Optimum_N: Calculates the optimal tally of throws for a given dice_sides value.
5. Random_dice_side: Generates a random number between 1 and the given dice_sides value.
6. Optimal_score_process: Calculates the optimal score for a given dice_sides value.
7. Evaluate_dice_throws: Loops through the dice game setup and casts dice, updating the scorecard and tally variables accordingly.
8. Calculate: Performs all necessary calculations based on user inputs and calls the Evaluate_dice_throws procedure, and saves items for the Report Card tables.
Main code description
1. Define constants, setup variables, and score logic, including dice_sides, dice_count, winner5, and loser5.
2. Initialize arrays and lists, such as dice_sides_array, dice_cast_array, and dice_tally_array.
3. Display the final state of variables and lists
4. Define the random_dice_side and optimal_score_process procedures.
5. Call the calculate procedure to perform all necessary calculations and display the results.
6. Display the final state of variables and lists, such as winner5, loser5, casts_tally, and tally_lister.
Conclusions
gold Update 2/21/2024. I have found it easier and more tidy to start with a working TCL math template and morf a few lines into a new purpose. If one completes and tests the new TCL subroutine in a console program, then usually one can load the new TCL subroutine into a graphical user interface (gui). I am not sure how to define winning at dice games, other than the pleasure of learning more TCL. It is said that game players need to win one out of three games to keep interest up.
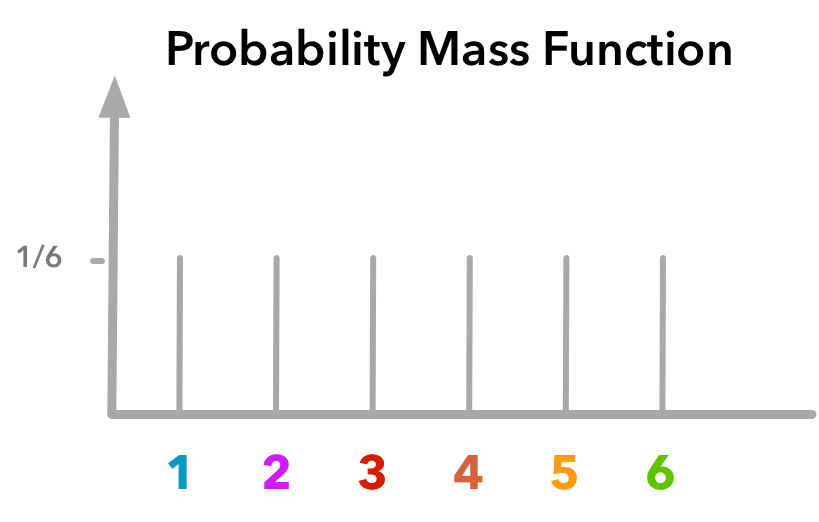
Table 1: Table for 6 sided single die mass probability function
Probability of a certain number with a Single Die.
Roll a single die Probability
| table 1 | Prob. Fraction | Prob. decimal printed in tcl wiki format |
|---|---|---|
| 1 | 1/6 | 16.667% |
| 2 | 1/6 | 16.667% |
| 3 | 1/6 | 16.667% |
| 4 | 1/6 | 16.667% |
| 5 | 1/6 | 16.667% |
| 6 | 1/6 | 16.667% |
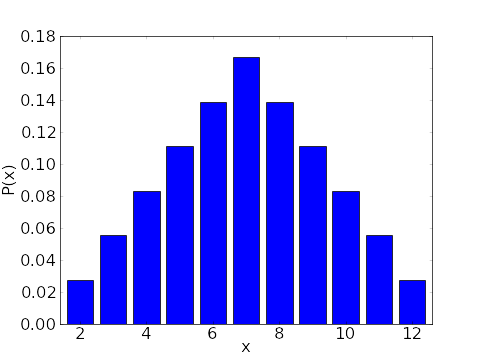
Table 2: Table for two 6-sided dice, mass probability function
| table 2 | Prob. fraction | Prob. Decimal | printed in tcl wiki format |
|---|---|---|---|
| 2 | 1/36 | 2.778 | |
| 3 | 2/36 | 5.556 | |
| 4 | 3/36 | 8.333 | |
| 5 | 4/36 | 11.111 | |
| 6 | 5/36 | 13.889 | |
| 7 | 6/36 | 16.667 | |
| 8 | 5/36 | 13.889 | |
| 9 | 4/36 | 11.111 | |
| 10 | 3/36 | 8.333 | |
| 11 | 2/36 | 5.556 | |
| 12 | 1/36 | 2.778 |
Table 3: Table for two 2-sided dice, mass probability function
| Table 3 | printed in TCL WIKI format |
|---|---|
| 1 | 0.0 |
| 2 | 0.25 |
| 3 | 0.5 |
| 4 | 0.25 |
Table 4: Table for two 20-sided dice, section of mass probability function
Note. Checking math here, value for 1 is really null, not zero.
| Table 4 | two 20-sided dice print TCL WIKI format |
|---|---|
| 1 | 0.0 |
| 2 | 0.0025 |
| 3 | 0.005 |
| 4 | 0.0075 |
| 5 | 0.01 |
| 6 | 0.0125 |
| 7 | 0.015 |
| 8 | 0.0175 |
| 9 | 0.02 |
| 10 | 0.0225 |
| 11 | 0.025 |
| 12 | 0.0275 |
| 13 | 0.03 |
| 14 | 0.0325 |
| 15 | 0.035 |
| 16 | 0.0375 |
| 17 | 0.04 |
| 18 | 0.0425 |
| 19 | 0.045 |
| 20 | 0.0475 |
| 21 | 0.05 |
| 22 | 0.0475 |
| 23 | 0.045 |
| section ends |
Table 5: List of casts on dice 64
Note. Checking math here,
2 8 3 20 4 42 5 32 6 51 7 39 8 25 9 13 10 49 11 34 12 26 13 8 14 23 15 11 16 17 17 42 18 54 19 63 20 40
3 6-sided dice "output 1",10.500000000004832,2.9580398915501926,3,18 #,% 3,0.462962962963 4,1.38888888889 5,2.77777777778 6,4.62962962963 7,6.94444444444 8,9.72222222222 9,11.5740740741 10,12.5 11,12.5 12,11.5740740741 13,9.72222222222 14,6.94444444444 15,4.62962962963 16,2.77777777778 17,1.38888888889 18,0.462962962963
Testcases Section
Testcase 1 , single 6-sided die
The estimated optimum for a 6 sided die is rounded 10. Sum of throws [+ 4 6 3\] or 13 would be a loss.
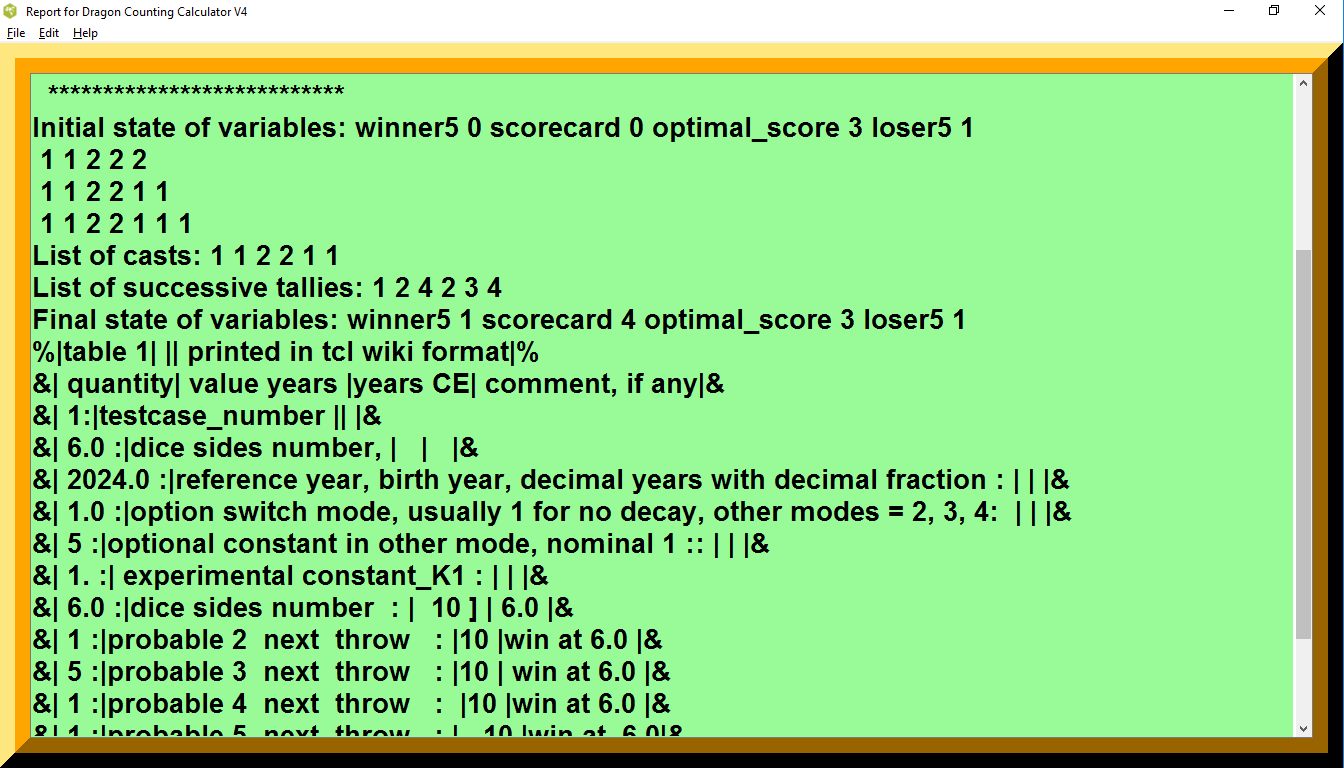
| table 1 | printed in tcl wiki format | ||
|---|---|---|---|
| quantity | value years | years CE | comment, if any |
| 1: | testcase_number | ||
| 6.0 : | dice sides number, | ||
| 2024.0 : | reference year, birth year, decimal years with decimal fraction : | ||
| 1.0 : | option switch mode, usually 1 for no decay, other modes = 2, 3, 4: | ||
| 3 : | optional constant in other mode, nominal 1 :: | ||
| 1. : | experimental constant_K1 : | ||
| 6.0 : | dice sides number : | 10 ] | 6.0 |
| 4 : | probable 2 next throw : | 10 | win at 6.0 |
| 6 : | probable 3 next throw : | 10 | win at 6.0 |
| 3 : | probable 4 next throw : | 10 | loss |
| 5 : | probable 5 next throw : | 10 | loss |
| 6 : | probable 6 next throw : | 10 | loss |
| 4 : | probable 7 next throw : | 10 | loss |
| 5 : | probable 8 next throw : | 10 | loss |
Testcase 2 , single 6-sided die
The estimated optimum for a 6 sided die is rounded 10. Sum of throws [+ 2 5 3 3\] or 13 would be a loss. iNTERESTING to have successive sums of 13?
| table 2 | printed in tcl wiki format | ||
|---|---|---|---|
| quantity | value years | years CE | comment, if any |
| 2: | testcase_number | ||
| 6.0 : | dice sides number, | ||
| 2024.2 : | reference year, birth year, decimal years with decimal fraction : | ||
| 1.0 : | option switch mode, usually 1 for no decay, other modes = 2, 3, 4: | ||
| 6 : | optional constant in other mode, nominal 1 :: | ||
| 1. : | experimental constant_K1 : | ||
| 6.0 : | dice sides number : | 10 ] | 6.0 |
| 2 : | probable 2 next throw : | 10 | win at 6.0 |
| 5 : | probable 3 next throw : | 10 | win at 6.0 |
| 3 : | probable 4 next throw : | 10 | win 6.0 |
| 3 : | probable 5 next throw : | 10 | loss |
| 1 : | probable 6 next throw : | 10 | loss |
| 3 : | probable 7 next throw : | 10 | loss |
| 6 : | probable 8 next throw : | 10 | loss |
Testcase 3 , single 6-sided die
The estimated optimum for a 20 sided die is rounded 34. Still using the 6 sided die, but Sum of throws were [+ 6 5 2 5 3 6 1\].
| table 3 | printed in tcl wiki format | ||
|---|---|---|---|
| quantity | value years | years CE | comment, if any |
| 3: | testcase_number | ||
| 20.0 : | dice sides number, | ||
| 2024.5 : | reference year, birth year, decimal years with decimal fraction : | ||
| 1.0 : | option switch mode, usually 1 for no decay, other modes = 2, 3, 4: | ||
| 4 : | optional constant in other mode, nominal 1 :: | ||
| 1. : | experimental constant_K1 : | ||
| 20.0 : | dice sides number : | 34 ] | 20.0 |
| 6 : | probable 2 next throw : | 34 | win at 20.0 |
| 5 : | probable 3 next throw : | 34 | win at 20.0 |
| 2 : | probable 4 next throw : | 34 | win 20.0 |
| 5 : | probable 5 next throw : | 34 | win at 20.0 |
| 3 : | probable 6 next throw : | 34 | win at 20.0 |
| 6 : | probable 7 next throw : | 34 | win at 20.0 |
| 1 : | probable 8 next throw : | 34 | win at 20.0 |
Screenshots Section
figure 1a. Dragon Counting Dice Game V2 vaporware screenshot
figure 1t. Dragon Counting Dice Game V4, second vaporware screenshot
figure 1r. Dragon Counting Dice Game V4, various flowcharts
figure 1z. Dragon Counting Dice Game V4, output display for tables in TCL Wiki format
figure 1c. Dragon Counting Dice Game 20 sides2
figure 2. Chinese Numbers
--- 
figure 3. Favorite camera on child, commercial game
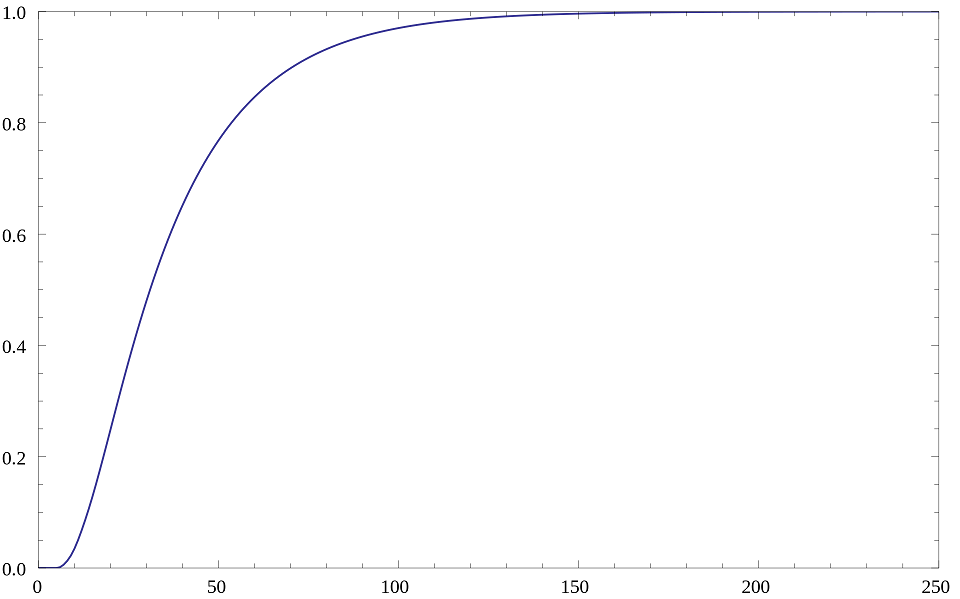
figure 4. from Wikipedia, Snakes and Ladders probability after N Turns, commercial game
Figures the number of turns for completion of Snakes and Ladders game. Y-axis is probability. X-axis is number of turns. Game Completion = 1, I think.
figure 5. from Wikipedia, Dragon Counting Dice Game V2 child snake ladder chase game jain
Gyan chaupar (Jain version of the game), National Museum, New Delhi, credit Nomu420 on Wikipedia. The association of Britain's snakes and ladders with India and gyan chauper began with the returning of colonial families from India during the British Raj. The décor and art of the early English boards of the 20th century reflect this relationship.
figure 6 . from Wikipedia, Dragon Counting Dice Game V2 child snake ladder chase game illustration
figure 7 . replicas , Dragon Counting Dice Game V2 6 sided single die mass probability function
The probability plot of a 6-sided dice. In the context of a probability plot, we are looking for the probability of each outcome (rolling a 1, 2, 3, 4, 5, or 6) and how they are distributed. Since a fair 6-sided dice is equally likely to land on any of its sides, the probability of rolling each number is the same. For a fair 6-sided dice: The probability of rolling a 1, 2, 3, 4, 5, or 6 is 1/6 or approximately 0.1667. A probability plot for a fair 6-sided dice would show a uniform distribution, with each number having an equal probability of being rolled.
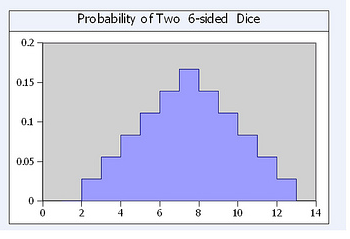
figure 8 . from Wikipedia, Dragon Counting Dice Game V3 two 6-sided dice mass probability function
The probability plot of rolling two 6-sided dice. In the context of a probability plot, we are looking for the probability of each outcome (rolling a 2, 3, 4, ..., 12) and how they are distributed. When rolling two 6-sided dice, the total number of possible outcomes is 6 * 6 = 36. The probability of each outcome is calculated by dividing the number of ways to achieve that outcome by the total number of possible outcomes (36). For example, there is only one way to roll a 2 (rolling a 1 on both dice) and one way to roll a 12 (rolling a 6 on both dice), so the
probability of rolling a 2 or a 12 is 1/36 or approximately 0.0278. Here is the probability distribution for rolling two 6-sided dice: Probability of rolling a 2: 1/36 or approximately 0.0278 Probability of rolling a 3: 2/36 or approximately 0.0556 Probability of rolling a 4: 3/36 or approximately 0.0833 Probability of rolling a 5: 4/36 or approximately 0.1111 Probability of rolling a 6: 5/36 or approximately 0.1389 Probability of rolling a 7: 6/36 or approximately 0.1667 Probability of rolling an 8: 5/36 or approximately 0.1389 Probability of rolling a 9: 4/36 or approximately 0.1111 Probability of rolling a 10: 3/36 or approximately 0.0833 Probability of rolling an 11: 2/36 or approximately 0.0556 Probability of rolling a 12: 1/36 or approximately 0.0278
A probability plot for rolling two 6-sided dice would show a bell-shaped distribution, with the most likely outcomes being rolling a 7, and the least likely outcomes being rolling a 2 or a 12.
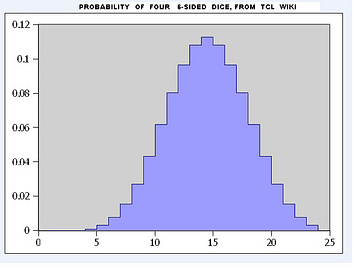
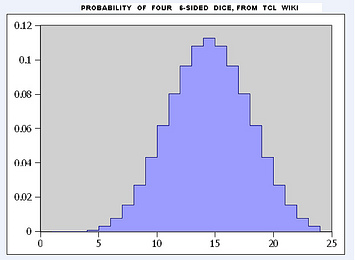
figure 9 . from Wikipedia, Dragon Counting Dice Game V3 6 2-sided stick dice for 64 space
figure 10 . from Wikipedia, Dragon Counting Dice Game V3 child snake ladder chase game board
figure 11. Stick Dice
figure 12. Chinese Abacus
figure 13. Replica Sundial with Hexagram Marks
figure 14. Stick Dice
test reload of images from offsite
Screenshots Section
figure 2.
figure 3.
figure 4.
figure 5.
figure 6.
figure. Space probability on space of 64
The probability plot of rolling six 2-sided dice. In the context of a probability plot, we are looking for the probability of each outcome (rolling a 1, 2, 3, ..., 64) and how they are distributed. When rolling six 2-sided dice, the total number of possible outcomes is 2 * 2 * 2 * 2 * 2 * 2 = 64. The probability of each outcome is calculated by dividing the number of ways to achieve that outcome by the total number of possible outcomes (64). For example, there is only one way to roll a 1 (rolling a 1 on all six dice) and one way to roll a 64 (rolling a 2 on all six dice), so the probability of rolling a 1 or a 64 is 1/64 or approximately 0.0156. A probability plot for rolling six 2-sided dice would show a bell-shaped distribution, with the least likely outcomes being rolling a 1 or a 64.
References:
- Primary references, Google <Babylonian Multiplication by M. Lewinter and W. Widulski>
- Mathematics
- Primary reference, Pi is Evil - Numberphile, Featuring James Munro with Dragons, Dice and Evil Numbers.
- James Munro is Admissions and Outreach Coordinator for Maths at Oxford University.
- snakes_probability/snakes_probability ,
- Desmond Higham, Nicholas Higham
- Steve Althoen, Larry King, Kenneth Schilling,
- How long is a game of Snakes and Ladders?,
- The Mathematical Gazette,
- Volume 77, Number 478, March 1993, pages 71-76.
- Nick Berry,
- A Mathematical Analysis of Snakes and Ladders,
- www.datagenetics.com/blog/november
- Dr. Math articles are locked behind pay wall, things getting tough.
- I did find an online IDE, https://www.jdoodle.com/execute-tcl-online/
- Monopoly from GWM
- S.K. Park & K.W. Miller, “Random number generators: good ones are hard to find,”
- Comm ACM 31(10):1192-1201, Oct 1988
- W.H. Press & S.A. Teukolsky, “Portable random number generators,”
- Computers in Physics 6(5):522-524, Sep/Oct 1992.
Pseudocode & Equations Section
more than one formula for 1) tables and 2) calculator shell
# recommended, avoids division by zero
product of 50*40*30 using modern base_60 logarithms,
# used in thinking pod
the sum of logs is expr { 0.95546+0.90096+0.830706} , 2.687126.
The antilog in base_60 is expr 60**2.687126= 59995.193.
For the tables, the int function is used to clip remainders to integers.
the precision function by [AM] is used occasionally, but not every time.
note: mental and undocumented components in the methods.
# exponent/ logarithm expressions
log (sqrt (m)) = (1/2)*log (m)
log (crt (m)) = (1/3)*log (m)
log (sqrt (m)) = (1/2)*log (m)
(1/2) = log (sqrt (m)) / log (m)
(1/2) = log (sqrt (m)) - (m))
log (crt (m)) = (1/3)*log (m)
(1/3) = log (crt (m)) / log (m)
(1/3) = log (crt (m)) - (m))
(1/2) = log (sqrt (m)) / log (m)
(2/1) = log (m) / log (sqrt (m))
2 = log (m - (sqrt (m))
(3/1) = log (m) / log (crt (m))
3 = log (m - (crt (m))
N = log (m - (N’rt(m))
N+1 = log (m - ((N+1)’rt(m))
log2 defined as ln N / ln 2 ,
log2 N =~ 1.442695 * ln N
log2 N =~ 3.321928 * log10 N
# find simple interest amount from 3 entries as < principal interest years >
proc simple_interest_amount { principal interest years } { expr { ($principal*1.)*(1.+$years*$interest )}}
# Dice in alternate procedures, checking math and format here
expr {1 + int(rand()*6)} RLE
# parens? weak eyes here.
proc dice_sides_N { dice_sides } { expr { 1 + int(rand()*$dice_sides)} }
proc dice_sides_N { dice_sides } { expr { 1 + int(rand()*$dice_sides)} }
proc optimum_N { dice_sides } { expr { int(1.718281828 *$dice_sides) }}
proc optimum_G { dice_sides } { expr { int(1.6180339887498948420 *$dice_sides) }}
# set g_constant .6180339887498948420
# golden ratio is 1.6180339887498948420 Appendix Code
Test Deck
Note. I did find a useful online IDE, https://www.jdoodle.com/execute-tcl-online/ . I can paste from local text file, edit, and run a test deck of TCL. I guess that we should stop computing chain and infinite loop after so long, but kind of interested in looking at the trajectory of sum of random throws. One might wonder how one can win and lose at same time. "take the money and run" was the old saying. keep playing and empty wallet. Multiple dice casts will fly past goalpost and winner, most times. Also a die with a large number of faces, sides >> 6, might be a problem here.
Note. There may be some kind of data type problem on the dice_sides variable. Still trying to resolve.
# Mock Up for Dragon Dice Deck V4
# pretty print from autoindent and ased editor
# throw N-sided dice until => chosen optimum number,
# declare winner or loser
# Multiple dice casts will fly past goalpost, most times.
# Dragon Counting Dice Game calculator V4
# written on Windows 10
# working under TCL version 8.6
# gold on TCL WIKI, 30jan2024
# Define globals
global winner5
global loser5 dice_sides
global dice_sides_array dice_cast_array dice_tally_array
global cast_lister tally_lister optimal_score
# Define constants and variables
set dice_sides [ expr { 2 * 1. }]
set dice_count 10
set winner5 0
set loser5 0
# Initialize arrays and lists
set dice_sides_array [list]
set dice_cast_array [list]
set dice_tally_array [list]
set cast_lister [list]
set tally_lister [list]
proc random_dice_side {dummy} {
global dice_sides
expr { 1 + int(rand()*$dice_sides)}
}
proc optimal_score_process {dummy} {
global dice_sides
expr { int(1.718281828 * $dice_sides ) }
}
# Define optimal score here, rounded integer
set optimal_score [ optimal_score_process 1 ]
# Loop through dice sides and cast dice
proc evaluate_dice_throws {dummy_variable} {
global winner5
global loser5 dice_sides
global dice_sides_array dice_cast_array dice_tally_array
global cast_lister tally_lister optimal_score
#set optimal_score [optimal_score $dice_sides]
set scorecard 0
puts "Initial state of variables: winner5 $winner5 scorecard $scorecard optimal_score $optimal_score loser5 $loser5"
foreach i { 4 5 6 7 8 9 10 11 12 } {
set cast_dice$i 0
set tally$i 1
}
foreach i { 4 5 6 7 8 9 10 11 12 } {
set side$i $i
set placeholder $i
set side$i $placeholder
set placeholder [random_dice_side $dice_sides]
set cast_dice$i $placeholder
lappend cast_lister $placeholder
puts " $cast_lister $placeholder"
set scorecard [ expr { $placeholder + $scorecard } ]
set tally$i $scorecard
lappend tally_lister $scorecard
# three if statements, not too fancy for my thinking pod
if { $scorecard < $optimal_score} { set loser5 0 }
if { $scorecard == $optimal_score} { set winner5 1 }
if { $scorecard > $optimal_score } { set loser5 1 ; break }
}
puts "List of casts: $cast_lister"
puts "List of successive tallies: $tally_lister"
puts "Final state of variables: winner5 $winner5 scorecard $scorecard optimal_score $optimal_score loser5 $loser5"
}
evaluate_dice_throws 1Multiple dice casts will fly past goalpost, most times.
initial state of variables = winner5 0 scorecard 0 goalpost 10 loser5 0 list casts 3 1 2 3 1 5 list successive tallies 3 4 6 9 10 15 finial state of variables = winner5 0 scorecard 15 goalpost 10 loser5 1 Initial state of variables: winner5 0 scorecard 0 optimal_score 10 loser5 0 1 1 1 4 4 1 4 3 3 1 4 3 1 1 1 4 3 1 2 2 List of casts: 1 4 3 1 2 List of successive tallies: 1 5 8 9 11 Final state of variables: winner5 1 scorecard 11 optimal_score 10 loser5 1 Initial state of variables: winner5 0 scorecard 0 optimal_score 10 loser5 0 2 2 2 4 4 2 4 5 5 List of casts: 2 4 5 List of successive tallies: 2 6 11 Final state of variables: winner5 0 scorecard 11 optimal_score 10 loser5 1 Initial state of variables: winner5 0 scorecard 0 optimal_score 10 loser5 0 1 1 1 6 6 1 6 5 5 List of casts: 1 6 5 List of successive tallies: 1 7 12 Final state of variables: winner5 0 scorecard 12 optimal_score 10 loser5 1 4 sided dice here, optimum left at 10 Initial state of variables: winner5 0 scorecard 0 optimal_score 10 loser5 0 1 1 1 3 3 1 3 1 1 1 3 1 2 2 1 3 1 2 1 1 1 3 1 2 1 1 1 1 3 1 2 1 1 4 4 List of casts: 1 3 1 2 1 1 4 List of successive tallies: 1 4 5 7 8 9 13 Final state of variables: winner5 0 scorecard 13 optimal_score 10 loser5 1 Initial state of variables: winner5 0 scorecard 0 optimal_score 3 loser5 0 1 1 1 2 2 1 2 2 2 List of casts: 1 2 2 List of successive tallies: 1 3 5 Final state of variables: winner5 1 scorecard 5 optimal_score 3 loser5 1
Test on printing list
set scale_factor [/ $real_estate $total_false_position ]
set counter 4
set real_scaled_results {}
foreach item $keeperlist {
lappend real_scaled_results [* $item $scale_factor ]
set side$counter [* $item $scale_factor ]
incr counter
if { [- $counter 4 ] > $number_of_brothers } {break}
}Trial Calculator Shell , Mock Up for Dragon Dice Deck V4
Error reconstruction on data type in List
set vals { 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 }
set a 1
set b 2
set c 3
set check_number 3
set check_number_2 4
puts [lindex $vals 0]
puts [lindex $vals 3]
puts [lindex $vals end]
puts [lindex $vals end-2]
puts "using check_number equals $check_number"
puts "using lindex check_number pulls [lindex $vals $check_number]"
puts "using lindex check_number_2 pulls [lindex $vals $check_number_2]"
set a [expr {$a << 0}]
set b [lrange $b 0 end]
set c [string range [append c \u1234] 0 end-1]
set d [ lindex $vals $check_number_2]
# Print the representations
puts [tcl::unsupported::representation $a]
puts [tcl::unsupported::representation $b]
puts [tcl::unsupported::representation $c]
puts [tcl::unsupported::representation $d]Based on twixt from Donal Fellows, thanks
output 1 4 15 13 using check_number equals 3 using lindex check_number pulls 4 using lindex check_number_2 pulls 5 value is a int with a refcount of 2, object pointer at 0x55bea895eb80, internal representation 0x1:0x55bea895e8b0, no string representation value is a list with a refcount of 2, object pointer at 0x55bea89603b0, internal representation 0x55bea8968c90:(nil), no string representation value is a string with a refcount of 2, object pointer at 0x55bea895e580, internal representation 0x55bea896cbe0:0x55bea895df80, no string representation value is a pure string with a refcount of 3, object pointer at 0x55bea895e340, string representation "5"
asdfasdf >>> one can write llength $a which forces a into a list representation. You really cannot rely on Tcl values having a particular type.
appendix : Script on Tables for TCL console
proc winnerx {aa bb} {
global sumit sumitland
#puts "end of game"
#.t insert 1.0 "end of game"
if { $sumit >= 500 } {
puts "winner declared"
}
if { $sumitland >= 500 } {
puts "winner declared"
}
}
appendix, counting through a list of thrown dice combos for probability
gold Here's counting through a list of thrown dice combos for probability. The worker bee is lsearch -all $lister $facen $facen is the sum of a 2-dice throw like 7. Subroutine is invoked by a foreach procedure for probability, which would be number of thrown 7's over all possible throws ($lister). Drop (-all) and lose all, returning only one position of "7" in list. See Binomial Probability Slot Calculator Example.
Other dice and random examples on Wiki. The random pick algorithm was posted by Suchenworth RS on Horseracing in Tcl. Using the random pick algorithm from Suchenworth RS is an alternate way to simulate dice play and sometimes easier for the non standard dice set ups. Other dice pages are Throwing Two Dice GWM and Dice by Keith Vetter. Also int from RLE has dice expression expr {1 + int(rand()*6)} RLE. Several Dr. Math emails may reduce some dice issues to simple paths.
console show
proc calculation { facen } {
# prob. subroutines for two 6-sided dice
set lister {2 3 4 5 6 7 3 4 5 6 7 8 4 5 6 /
7 8 9 5 6 7 8 9 10 6 7 8 9 10 11 7 8 9 10 11 12}
set ee [llength $lister ]
set kk [ llength [ lsearch -all $lister $facen ] ]
set prob [ expr { ($kk*1.) / $ee } ]
return $prob
}
set limit 12
for { set i 1 } { $i <= $limit } { incr i } {
lappend listxxx $i
lappend listxxx [ calculation $i ]
puts " $i [ calculation $i ] "
}
#end Appendix on Stick Dice
Note on 13Feb2024.
2 yes-no binary sticks equals 2**2 combinations or 16 combinations. Probability of single cast 1/(2**2) or 1/4. Space = 4 items
4 yes-no binary sticks equals 2**4 combinations or 16 combinations. Probability of single cast 1/(2**4) or 1/16. Space = 16 items
5 yes-no binary sticks equals 2**5 combinations or 32 combinations. Probability of single cast 1/(2**5) or 1/32. Space = 32 items
6 yes-no binary sticks equals 2**6 combinations or 64 combinations. Probability of single cast 1/(2**6) or 1/64. Space = 64 items
7 yes-no binary sticks equals 2**7 combinations or 128 combinations. Probability of single cast 1/(2**7) or 1/128. Space = 128 items
Chinese excavations reveal a possible related divination system with space of 60 combinations.
There are current Buddhist temple methods that picking a stick from 64 sticks or some other number. Popular Game of Pick up Sticks in West. In that case, the classic formula would be 1/64 for equal Hexagram probability and the probability space would 64 items.
Bernoulli probability formula, P(Yang)= 1- P(Yin) The three most frequently occurring characters are: 吉 auspicious 无咎 no misfortune 凶 ominous Thinking in Bullet Points There are a total of 384 lines in the I Ching Oracle Book There are roughly 100 lines with character "mistake", Chinese "Liu" 100/384 = 0.2604 probability of mistake Liu appearing (384-100)= 284 number of lines without mistake Liu appearing 284/384= 0.7396 probability of mistake Liu not appearing The probability of casting a line with the character "mistake" is 0.2604, roughly 1/4 or 0.25 The probability of casting a line with no character "mistake" is 0.7396, roughly 3/4 or 0.75 The probability of casting a line with or without character "mistake" is 0.2604 + 0.7396 = 1 One might conclude the I Ching Oracle Book is rigged not to cast a character "mistake".
Appendix. Still Proof Reading Here
The probability space of hexagram diagrams generated by the cast of binary dice. No direct experience with this specific problem, but some general guidance can be provided on how to approach this type of question. First, it's essential to clarify the problem statement and ensure that one have a clear understanding of the rules and constraints. In this case, one is considering dice marked with binary digits (0 or 1), and one want to calculate the probability space for the sum of the dice throws as they form the bars of a hexagram diagram.To solve this problem, one can use combinatorics and probability theory. one will need to determine the number of possible outcomes for each die throw and then calculate the probability of each outcome. This will help one to find the probability space for the hexagram diagrams. Here's a step-by-step approach to solving this problem:
Determine the number of sides on each die and the number of dice being cast. In this case, one have 6 dice, each with 2 sides (0 or 1).
Calculate the total number of possible outcomes for each die throw. Since each die has 2 sides, there are 2^6 = 64 possible outcomes for the 6 dice cast.
Determine the probability of each possible outcome. The probability of a single outcome is 1/(2^6), or 1/64.
Calculate the probability space for the hexagram diagrams by considering the sum of the dice throws. one can use combinatorics to determine the number of ways to achieve each possible sum and then multiply that number by the probability of each outcome.
Analyze the results and compare them to the Chinese diagnostics for the 64 diagrams, if applicable.
Regarding references for similar dice problems, it's likely that there is existing literature on combinatorics and probability theory that covers this type of problem. one may want to consult textbooks or research papers in these fields for more specific examples and solutions.
As for the distribution of 6 dice, it is indeed a binomial distribution. In a binomial distribution, there are a fixed number of trials (in this case, 6 dice throws), each with a binary outcome (success or failure). The probability of success for each trial is constant, and the trials are independent. In this problem, the probability of success (rolling a 1) is 0.5, and the probability of failure (rolling a 0) is also 0.5. The binomial distribution can be used to calculate the probability of observing a specific number of successes in the 6 dice throws. I hope this guidance helps one in research and analysis of hexagram diagrams and binary dice problems.
To create a probability plot for rolling three 4-sided dice with the given markings, we can follow these steps: Calculate the probability of each outcome by dividing the number of ways to achieve that outcome by the total number of possible outcomes (64).
Create a bar chart with the outcomes on the x-axis and their respective probabilities on the y-axis.
Label the x-axis with the outcomes and the y-axis with the probabilities.
Add a hexagram diagram with the sum of each cast as the base bar and the sum of the sixth dice throw as the top bar.
Check for accuracy? >>> Here's an example probability plot for rolling three 4-sided dice with the given markings, specifically for the 64 diagrams in the Chinese I Ching Oracle Book: Probability Plot for Rolling Three 4-Sided Dice with Given Markings Specific to the 64 Diagrams in the Chinese I Ching Oracle Book In this plot, the x-axis represents the possible outcomes (ranging from 1 to 16), and the y-axis represents the probability of each outcome. The bar chart shows the probability distribution, with the most likely outcomes being rolling a 10 or a 11 and the least likely outcomes being rolling a 1 or a 16. The hexagram diagram at the top represents the sum of each cast, with the base bar being the sum of the first dice throw and the top bar being the sum of the sixth dice throw.
Test Deck
Note. I did find a useful online IDE, https://www.jdoodle.com/execute-tcl-online/ . I can paste from local text file, edit, and run a test deck of TCL. I guess that we should stop computing chain and infinite loop after so long, but kind of interested in looking at the trajectory of sum of random throws. One might wonder how one can win and lose at same time. "take the money and run" was the old saying. keep playing and empty wallet. Multiple dice casts will fly past goalpost and winner, most times. Also a die with a large number of faces, sides >> 6, might be a problem here. Note. there is some kind of data type problem on the dice_sides variable.
Text has been pretty printed, omitting blank lines. may have to check for typos. Code is written for Windows 10 and may be Windows 10 dependent. This is not a deck from Unix.
# Mock Up for Dragon Dice Deck V4
# pretty print from autoindent and ased editor
# throw N-sided dice until => chosen optimum number,
# declare winner or loser
# Multiple dice casts will fly past goalpost, most times.
# Dragon Counting Dice Game calculator V4
# written on Windows 10
# working under TCL version 8.6
# gold on TCL WIKI, 30jan2024
# Define globals
global winner5
global loser5 dice_sides
global dice_sides_array dice_cast_array dice_tally_array
global cast_lister tally_lister optimal_score
# Define constants and variables
set dice_sides [ expr { 2 * 1. }]
set dice_count 10
set winner5 0
set loser5 0
# Initialize arrays and lists
set dice_sides_array [list]
set dice_cast_array [list]
set dice_tally_array [list]
set cast_lister [list]
set tally_lister [list]
proc random_dice_side {dummy} {
global dice_sides
expr { 1 + int(rand()*$dice_sides)}
}
proc optimal_score_process {dummy} {
global dice_sides
expr { int(1.718281828 * $dice_sides ) }
}
# Define optimal score here, rounded integer
set optimal_score [ optimal_score_process 1 ]
# Loop through dice sides and cast dice
proc evaluate_dice_throws {dummy_variable} {
global winner5
global loser5 dice_sides
global dice_sides_array dice_cast_array dice_tally_array
global cast_lister tally_lister optimal_score
set scorecard 0
puts "Initial state of variables: winner5 $winner5 scorecard $scorecard optimal_score $optimal_score loser5 $loser5"
foreach i { 4 5 6 7 8 9 10 11 12 } {
set cast_dice$i 0
set tally$i 1
}
foreach i { 4 5 6 7 8 9 10 11 12 } {
set side$i $i
set placeholder $i
set side$i $placeholder
set placeholder [random_dice_side $dice_sides]
set cast_dice$i $placeholder
lappend cast_lister $placeholder
puts " $cast_lister $placeholder"
set scorecard [ expr { $placeholder + $scorecard } ]
set tally$i $scorecard
lappend tally_lister $scorecard
# three if statements, not too fancy for my thinking pod
if { $scorecard < $optimal_score} { set loser5 0 }
if { $scorecard == $optimal_score} { set winner5 1 }
if { $scorecard > $optimal_score } { set loser5 1 ; break }
}
puts "List of casts: $cast_lister"
puts "List of successive tallies: $tally_lister"
puts "Final state of variables: winner5 $winner5 scorecard $scorecard optimal_score $optimal_score loser5 $loser5"
}
evaluate_dice_throws 1Multiple dice casts will fly past goalpost, most times.
initial state of variables = winner5 0 scorecard 0 goalpost 10 loser5 0 list casts 3 1 2 3 1 5 list successive tallies 3 4 6 9 10 15 finial state of variables = winner5 0 scorecard 15 goalpost 10 loser5 1 Initial state of variables: winner5 0 scorecard 0 optimal_score 10 loser5 0 1 1 1 4 4 1 4 3 3 1 4 3 1 1 1 4 3 1 2 2 List of casts: 1 4 3 1 2 List of successive tallies: 1 5 8 9 11 Final state of variables: winner5 1 scorecard 11 optimal_score 10 loser5 1 Initial state of variables: winner5 0 scorecard 0 optimal_score 10 loser5 0 2 2 2 4 4 2 4 5 5 List of casts: 2 4 5 List of successive tallies: 2 6 11 Final state of variables: winner5 0 scorecard 11 optimal_score 10 loser5 1 Initial state of variables: winner5 0 scorecard 0 optimal_score 10 loser5 0 1 1 1 6 6 1 6 5 5 List of casts: 1 6 5 List of successive tallies: 1 7 12 Final state of variables: winner5 0 scorecard 12 optimal_score 10 loser5 1 4 sided dice here, optimum left at 10 Initial state of variables: winner5 0 scorecard 0 optimal_score 10 loser5 0 1 1 1 3 3 1 3 1 1 1 3 1 2 2 1 3 1 2 1 1 1 3 1 2 1 1 1 1 3 1 2 1 1 4 4 List of casts: 1 3 1 2 1 1 4 List of successive tallies: 1 4 5 7 8 9 13 Final state of variables: winner5 0 scorecard 13 optimal_score 10 loser5 1 Initial state of variables: winner5 0 scorecard 0 optimal_score 3 loser5 0 1 1 1 2 2 1 2 2 2 List of casts: 1 2 2 List of successive tallies: 1 3 5 Final state of variables: winner5 1 scorecard 5 optimal_score 3 loser5 1
Test on printing list of dice throws
# Test on printing list of dice throws
# still checking here.
proc initialize_seed {} {
# srand function uses integer seed
# set srand_yada [ expr { srand (1235) } # old 1st statement
# trying for seed as some integer below 1000000000.
# maybe time expensive invoking many times
set srand_yada [expr {int(rand()*1000000000.)}]
set dummy $srand_yada
set srand_yada [ expr { srand ($dummy) } ]
}
proc cast_dice {num_sides number_dice} {
set num_throws 0
set total 0
initialize_seed
while {$num_throws < $number_dice} {
set total [expr $total + [expr { int($num_sides*rand())+1 } ]]
incr num_throws
}
return $total
}
proc cast_dice_set {num_sides num_dice number_throws} {
set all {}
set num_throws 0
while {$num_throws < $number_throws } {
lappend all [cast_dice $num_sides $num_dice ]
incr num_throws
}
return $all
}
puts " throws [ cast_dice_set 6 3 1000 ] "To use this program, simply call the cast_dice_set procedure with the desired number of sides and the number of dice in the set. The program will then throw the dice multiple times and return the results. still checking here. Example usage: puts " puts " throws cast_dice_set 6 10 5 " "
set of 10 6-sided dice thrown 5 dimes. maximum number on a set = 60. still checking here. Minimum total for snake eyes = 6
# Test on printing list of dice throws
# still checking here
puts " throws [ cast_dice_set 6 10 5 ] " # 6 sides, 10 dice, 5 throws.
throws 27 35 40 36 30 # 6 sides, 10 dice, 5 throws.
puts " throws [ cast_dice_set 6 1 5 ] " # 6 sides, 1 die, 5 throws.
throws 6 4 1 4 6
puts " throws [ cast_dice_set 6 2 5 ] " # 6 sides, 2 dice, 5 throws.
throws 11 10 4 5 4
puts " throws [ cast_dice_set 4 2 10 ] "
# For 2 4-sided dice, max should be 8,
# min should be 2,
# 10 throws are counted here
throws 6 5 6 6 8 2 3 7 6 6
puts " throws [ cast_dice_set 2 6 15 ] "
throws 10 8 9 7 8 7 6 8 9 11 10 9 8 6 10
puts " throws [ cast_dice_set 2 6 30 ] "
throws 9 7 9 7 10 10 10 10 7 10 8 10 10 11 9 8 9 8 10 8 10 10 8 9 9 9 11 9 10 11
puts " throws [ cast_dice_set 2 6 100 ] "
# a set of 6 2-sided dice.
# min number should be 6, max number should be 12, 100 numbers,
throws 9 12 10 11 8 12 9 8 8 10 6 9 8 9 10 9 11 10 9 9 8 8 10 10 9 6 10 7 8 10
cont. 10 9 8 10 10 9 9 9 10 8 9 9 7 9 8 10 10 9 11 11 8 7 9 11 8 7 8 11 9 9 8 10
cont. 7 10 10 10 9 10 10 7 8 9 9 9 10 8 9 10 10 10 10 12 9 9 10 10 10 9 7 10 10 10
cont. 11 7 8 11 10 11 10 10
# set of 3 6-sided dice with 100 throws. min should be 3? , max =18?, most common between 10 and 12?
# something seems wrong here? looking for number 3 in 200 throws, triple snake eyes for sum { 1 1 1} = 3
puts " throws [ cast_dice_set 6 3 100 ] "
throws 8 16 12 9 13 13 9 11 10 8 13 8 7 12 9 15 13 7 9 10 10 13 13 17 7 8 8 8 14
cont. 10 6 12 12 11 9 7 12 12 8 8 12 13 11 9 10 11 9 12 8 9 10 14 9 6 5 13 15 10
cont. 10 12 10 15 6 11 8 12 12 13 9 5 15 7 17 12 14 8 10 10 12 14 12 8 7 7 15 9
cont. 16 11 10 11 14 9 8 7 12 11 12 14 11 11
dummy 534769070 srand_yada 534769070 srand value 0.30021033962267
dummy 77374940 srand_yada 77374940 srand value 0.564851865901077
dummy 28732348 srand_yada 28732348 srand value 0.8699651383189322
dummy 668325065 srand_yada 668325065 srand value 0.5587440196232609
dummy 573358426 srand_yada 573358426 srand value 0.31475987905392416
dummy 667009657 srand_yada 667009657 srand value 0.26387528482073697
dummy 287128559 srand_yada 287128559 srand value 0.17412766077282263
dummy 160567037 srand_yada 160567037 srand value 0.6569224538546625
dummy 721947559 srand_yada 721947559 srand value 0.22818267495752437
dummy 564889045 srand_yada 564889045 srand value 0.03025677429058439
throws 11 9 7 8 9 13 10 16 9 11 David T. Ashley recommends the recurrence. Reference the C. code definition for rand.
Draft. From this C. code snippet, the variable x is set to an initial seed value (e.g., 12345). The random number is generated by multiplying the seed value by 16807, taking the modulus division by 2147483647, and storing the result in the variable randx. This approach uses modulus division to ensure that the generated random number falls within a specific range. The modulus operator % in TCL returns the remainder of the division operation, which will be an integer value. """ Lehmer suggested that the (Mersenne) prime m = (2**31) - 1 might be an appropriate choice for the modulus. a = 7**5 = 16807 was first suggested by Lewis, Goodman and Miller in 1969 , based largely on the fact that j(z) = 168072 mod 2147483645 """" >>> ? But I am seeing a fraction from expr {rand} in TCL? <<<< In TCL, it's important to note that the rand function in TCL generates a random floating-point number between 0 and 1. If you need an integer random number, you can multiply the result of rand by a suitable range and then convert it to an integer using the int function. This can help in generating integer random numbers within a desired range.
# ~~~~ C. code definition for rand
x = (16807 * x) MOD 2147483647
# C. code pronounced as “x mod y”. For example, 10 % 2 will be pronounced as ” Ten mod Two”.
# not sure C. code mod is exactly as TCL % or fmod?
# set a 2.9999383
# expr {fmod($a,1)} result 0.9999383000000002# Pseudocode
# this is the "Lehmer" algorithm in Pseudocode
#
const a = 16807.0
const m = 2147483647.0
function Random(seed):
temp = a * seed
seed = temp - m * Truncate (temp / m)
return seed / m# tcl
# this is the "Lehmer" algorithm in TCL
#
# constants field
# real constants, not integer arithmetic?
set a 16807.0
set m 2147483647.0
# proc to generate random number
proc randomx {seed} {
set a 16807.0
set m 2147483647.0
set temp [expr {$a * $seed}]
set seed [expr {$temp - $m * int($temp / $m)}]
return [expr {$seed / $m}]
}
# Usage example
set seed 12345
set random_num [randomx $seed]
puts "Random number generated: $random_num"
# Random number generated: 0.09661652850760917
# Unlike rand in Tcl, this randomx procedure expects a seed value
# every time invoked. Not defaulted to blank entry, though a default
# could be loaded up. Or maybe, deck run twice for seed? and randomx?One Liner Programs & Simple One Liner Procedure
These one liner procedures demonstrate the simplicity and conciseness of TCL programming, while still being able to perform useful tasks.
Appendix: Test on Pretty Print
This program, called "math::quantity_into_ratios," takes a quantity and a list of ratios as arguments and returns the parts of the quantity divided by the ratios.
package require Tk
console show
package require math::numtheory
namespace path {::tcl::mathop ::tcl::mathfunc math::numtheory }
set tcl_precision 17
proc ::math::quantity_into_ratios {quantity args} {
set sum 0.
set N [ expr { [ llength $args ] + 1 } ]
if { $N == 1 } { return 0 }
foreach val $args {
set sum [ expr { $sum + $val } ]
}
foreach val $args {
lappend answer [ expr { $quantity * ($val/$sum) } ]
}
set answer
}Comments Section
Please place any comments here with your wiki MONIKER and dates, Thanks,gold 24FEB2024
under test
gold 2/20/2024. This a big file. Check earlier editions, if not compatible. Maybe obvious and stated in TCL deck, but this page was written on Windows10 Tcl ports including ActiveTCL. I assume that the reader can cut and paste on screen, what the reader needs, and tootle on to his own bio-project and own contribution pages to the TCL Wiki. The author is retired engineer and no longer has { proofing access } to Unix machines. Unix is respected after use of so many years in engineering, but my wings are lost.
.
gold 2024-02-20. These calculator approaches in TCL console guis for Windows10 may seem trivial math to some, but I have submitted 4 or 5 TCLLIB tickets to improve the TCLLIB math library. For example, the math and logic functions IsOdd, IsEven, IsNegative, IsPositive, figurative_numbers, and Quadratic_Equation_Solution_for_reals were not in the TCLLIB library, as near as I can tell. Maybe these logic functions on integers and Quadratic_Equations_Solutions on reals are trivial math to some, but these Quadratic_Equations_Solutions and other math functions show up in some other math languages, TCL programs, and even TCL WIKI pages. As HE implies, the main idea of TCL or other computer language is that other users can share the faster compiled code rather than homebrew functions. Since I am retired and I do not have easy access to a UNIX machine, the only course in the USA retirement economy is to proof and study the TCL routines on a Windows10 PC.
the probability plot of rolling a 20-sided dice. In the context of a probability plot, we are looking for the probability of each outcome (rolling a 1, 2, 3, ..., 20) and how they are distributed. Since a fair 20-sided dice is equally likely to land on any of its sides, the probability of rolling each number is the same. For a fair 20-sided dice: The probability of rolling a 1, 2, 3, ..., or 20 is 1/20 or approximately 0.05 A probability plot for a fair 20-sided dice would show a uniform distribution, with each number having an equal probability of being rolled.
The probability plot of rolling three 6-sided dice. In the context of a probability plot, we are looking for the probability of each outcome (rolling a 3, 4, 5, ..., 18) and how they are distributed. When rolling three 6-sided dice, the total number of possible outcomes is 6 * 6 * 6 = 216. The probability of each outcome is calculated by dividing the number of ways to achieve that outcome by the total number of possible outcomes (216). For example, there is only one way to roll a 3 (rolling a 1 on all three dice) and one way to roll an 18 (rolling a 6 on all three dice), so the probability of rolling a 3 or an 18 is 1/216 or approximately 0.00463. Here is the probability distribution for rolling three 6-sided dice:
Probability of rolling a 3: 1/216 or approximately 0.00463 Probability of rolling a 4: 3/216 or approximately 0.0139 Probability of rolling a 5: 6/216 or approximately 0.0278 Probability of rolling a 6: 10/216 or approximately 0.0463 Probability of rolling a 7: 15/216 or approximately 0.0694 Probability of rolling a 8: 21/216 or approximately 0.0977 Probability of rolling a 9: 25/216 or approximately 0.1164 Probability of rolling a 10: 27/216 or approximately 0.1250 Probability of rolling a 11: 27/216 or approximately 0.1250 Probability of rolling a 12: 25/216 or approximately 0.1164 Probability of rolling a 13: 21/216 or approximately 0.0977 Probability of rolling a 14: 15/216 or approximately 0.0694 Probability of rolling a 15: 10/216 or approximately 0.0463 Probability of rolling a 16: 6/216 or approximately 0.0278 Probability of rolling a 17: 3/216 or approximately 0.0139 Probability of rolling a 18: 1/216 or approximately 0.00463
# Pseudocode const a = 16807.0 const m = 2147483647.0
function Random(seed):
temp = a * seed
seed = temp - m * Truncate(temp / m)
return seed / m
# tcl
# Constants
set a 16807.0
set m 2147483647.0
# Function to generate random number
proc randomx {seed} {
set a 16807.0
set m 2147483647.0
set temp [expr {$a * $seed}]
set seed [expr {$temp - $m * int($temp / $m)}]
return [expr {$seed / $m}]
}
# Usage example
set seed 12345
set random_num [randomx $seed]
puts "Random number generated: $random_num"
# Random number generated: 0.09661652850760917A probability plot for rolling three 6-sided dice would show a bell-shaped distribution, with the most likely outcomes being rolling a 10 or a 11 and the least likely outcomes being rolling a 3 or an 18.
1. Functional vs. Imperative Programming Functional programming computes expressions, while imperative programming modifies memory with instructions. Functional relies on automatic garbage collection, while imperative requires explicit memory management.
2. Memory and Execution Control Imperative programming offers more control over execution and memory, but may be less efficient. Functional programming provides higher abstraction, execution safety, stricter typing, and automatic memory management.
3. Historical Perspectives Historically, symbolic applications were linked to functional programming, while numerical applications were associated with imperative programming. Advances in compiling and garbage collection have enhanced efficiency for both paradigms.
4. The Appeal of Tool Control Language TCL TCL highlights the balance between efficiency and assurance, gaining popularity among software developers. It demonstrates that maintaining good efficiency does not have to compromise on reliability.
proc optimal_score_process {dice_sides} { expr { int((exp(1)-1)*1. * $dice_sides ) }}
puts " optimal_score_process [ optimal_score_process 6 ]" # answer = 10
# optimal_score_process for 20 = 34Functional and Imperative Programming Functional programming computes an expression, while imperative programming is a sequence of instructions modifying memory. The former relies on an automatic garbage collector, while the latter requires explicit memory allocation and deallocation. Memory and Execution Control Imperative programming provides greater control over execution and memory representation, but can be less efficient. Functional programming offers higher abstraction and execution safety, with stricter typing and automatic storage reclamation. Historical Perspectives Historically, functional programming was associated with symbolic applications, and imperative programming with numerical applications. However, advances in compiling and garbage collection have improved efficiency and execution safety for both paradigms. The Appeal of Tool Control Language TCL TCL emphasizes that efficiency need not preempt assurance, as long as efficiency remains reasonably good. This approach is gaining popularity among software producers.
gold prompt? Improve, elaborate, explain steps, and explain definitions in numbered steps with numbered steps with details, dates, and elaboration in regard to computer applications, and Tool Control Language TCL ; use titles on each paragraph consisting of 1,2,3 or 4 words? Restrict each paragraph to 30 words or less?
gold prompt? improve, condense, elaborate, explain steps, and explain definitions in numbered steps with numbered steps with details, dates, and elaboration in regard to computer applications, and Tool Control Language TCL ; use titles on each paragraph consisting of 1,2,3 or 4 words? Restrict each paragraph to 30 words or less? Restrict text to third person and impersonal discussion text, substitute one for you, substitute ones for your, use one for he, use ones for his?
..
gold Prompt: improve, condense, elaborate, explain steps, and explain definitions in numbered steps with numbered steps with details, dates, and elaboration in regard to computer applications, and Tool Control Language TCL ; use titles on each paragraph consisting of 1,2,3 or 4 words? Omit blank lines? Restrict each paragraph to 30 words or less? Restrict text to third person and impersonal discussion text, substitute one for you, substitute ones for your, use one for he, use ones for his?