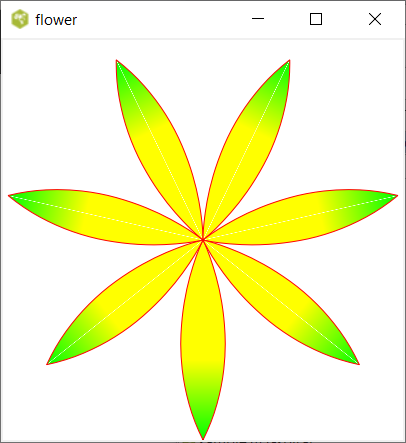
Drawing a flower with Blend2d

Arjen Markus (16 july 2024) With the new version of Blend2d that was published a few days ago I experimented a bit with the various geometries and other features. Notably:

A path object (I led myself be inspired by one of the examples) that contains a canonical petal
Various transformations, among which a rotation over 360/7 degrees to achieve a flower with seven petals
A colour gradient, just for good measure.

The code:

# flower.tcl --
#     Draw a simple flower using a single petal.
#     Use the transformation matrix to rotate it about the centre.
#     For good measure add a colour gradient.
#     The trick is to realise how the transformations are applied.
#
#     Note: I know of no natural flower that has seven petals, so
#     as far as I am concerned this is a completely new species.
#

set thisDir [file normalize [file dirname [info script]]]
set auto_path [linsert $auto_path 0 [file dirname $thisDir]]

# --flower - demo

package require Blend2d
set sfc [image create blend2d -format {400 400} ]
label .x -image $sfc ; pack .x

$sfc clear -fill.style 0xFFFFFFFF

set petal [BL::Path new]
$petal moveTo {0 0}
$petal cubicTo {0 0} {0.25  0.5} {0  1}
$petal moveTo {0 0}
$petal cubicTo {0 0} {-0.25 0.5} {0  1}

set transform [Mtx::MxM [Mtx::scale 200 200] [Mtx::translation 200 200]]
set rotation  [Mtx::rotation [expr {360.0/7.0}] degrees]

$sfc applyTransform $transform

for {set n 0} {$n < 7} {incr n} {
    #
    # For a uniform colour:
    #
    # $sfc fill   $petal  -fill.style 0xFFFFFF00

    #
    # Use the gradient:
    #
    set gradient [BL::gradient LINEAR {0.0 0.0 0.0 1.0} [list 0.0 [BL::color yellow] 0.6 [BL::color yellow] 1.0 [BL::color lime]]]
    $sfc fill   $petal  -fill.style $gradient
    $sfc stroke $petal  -stroke.style 0xFFFF0000 -stroke.transformorder BEFORE

    $sfc applyTransform $rotation
}

$petal destroy

And the resulting picture:

Flower-blend2d

This can actually be improved:

The petals show a thin yellow line in the middle. Redefining the path object eliminates that (see below).
The gradient needs to be computed once only, so you can move the computation out of the loop.

The path is better defined in this way:

set petal [BL::Path new]
$petal moveTo {0 0}
$petal cubicTo {0 0} {0.25  0.5} {0 1}

# Original:

#$petal moveTo {0 0}
#$petal cubicTo {0 0} {-0.25 0.5} {0 1}

# Improvement: reverse the order of the points

$petal cubicTo {0 1} {-0.25 0.5} {0 0}

Note: It may not be immediately clear. but the transformations are stacked and then applied last one first. For this reason adding a rotation over 360/7 degrees each iteration leads to the petals being rotated in steps over 360/7 * n degrees.