Finite State Machine
A finite state machine is a kind of state transition system
See Also
- Finomaton
- comfortably draw and typeset finite state machines

Finite State Machines
Examples
- Splitting strings with embedded strings
- includes a great example of a finite state machine that parses HTML
- Building a Respirometer using FSM, Tcl and Arduino™
- A very detailed example.
- ycl graph navigate
- A cross between a finite state machine and make. Navigate from the currnent node to some target node while tracking and avoiding dead ends.
Utilities
Misc
The mathematical model for a Finite State Machine is a mapping (D, Domain; R, Range) where
from (Din,Dstate) |--> to (Rout,Rstate) FSM(in,state) --> (out,new state)
schematically the machine applies the mapping like:
|----|
in -->| |--> out
| |
state -->| |--> next state
|----|Or machinewise,
clock ------ or 'trigger new state'
|
V
|----|
in -->| |--> out
| |
state -->| |--> next state
| |----| |
| |
-<---------The mappings from (in,state) to out and another to next_state are functions acting on domains which are respectively all possible inputs and all states (possibly minus the first or last), and which have ranges of all possible output values and all possible new state values.
From straightforward reasoning one may take it that it holds that
Domain(state) is subset of Range(newstate) minus newstate(initial)
Surely you rather meant to write
Dstate is superset of Rstate union initial_states
or something to that effect? - Lars H
{Let's see, the domain of the variable state is a subset (or equal to) of the Range for newstate (because the last state need not be in the domain of the newstate function), except that the initial state need not be in the range for newstate. Maybe nicer put, the domain for the variable state and range for the function newstate are the same except not necessarily for the initial state and the final state}
and it makes most sense practically to take
Domain(state) equals range Range(newstate) except for state(inital) and state(final)
The sequence of states which are traversed by starting from a given input and initial state is predictable and known when the model is not ill-defined. It can be a repeating sequence, or, by a changing input, infinite sequence without repetition, for instance by taking as states range and domain the decimal numbers 0 to 9 mapped to the some random output and a newstate equal to the previous input, and feeding the input with the decimals of PI.
DKF: So you have decided to stick to deterministic machines? In general, a FSM will be nondeterministic (though that is modellable as a hidden variable, it is often easier to use nondeterminism) and will have a set of terminating states (i.e., states that are not in the domain of the state input variable).
KPV: Actually a nondeterministic state machine (NDSM) can be modelled with a DSM. From a programming perspective, an NDSM can be much simpler than its equivalent DSM. Most of the faster versions of grep build an NDSM to do their searches.
TV: As a computer designer I am very certain, see also the pages on such subjects, that a computer by design is very much made into a deterministic machine, primarily. Really.
When you analyse the indeterministic aspect of what you mean I think you'd find that that is a matter of taking not the basic computer way out of the problem, a processor ticks quite deterministically in practice, and when done with so many layers of network processing, even that is quite deterministic in the end for many applications. But of course not overall, that is agreed.
The 'hidden variable' of course is a nice physicist touch, which I think you refer to as something that in nature reflects that which is behind the equations and makes up for an influence which isn't sheer randomness but isn't yet captured or even represented.
I disagree that most FSM's are inderministic, primarily because that is incorrect by the definition I gave, which quite a correct one, and practically because there is no need to introduce indeterminism so quickly, a lot of software and most 'everything' in computer hardware with notable exceptions can be completely modeled as a decent finite state machine, heck, the pentium or PA risc or sparc IS a FSM. For 99.9 percent of so. If they weren't programming them would be a lot harder I'm sure.
The hidden variable idea is interesting of course, for instance not the whole state is needed to progress between related states. But that's like limiting interest, not defining relevant information away.
The state and input variable have distinct domains as I defined, the only thing is that the range of the newstate function is the same as its 'state' argument.
A way to allow nondeterminism which is not needed that soon, but can be important, without losing mathematical grip from the start is to add a select function to resolve the ambiguity for finding a new state when two inputs arrive simulaneously.
Defining 'out of input range' or 'out of state domain range' inputs or states is mathematically not very challenging or interesting. Defining the problem and the mathematical model such that an adequate and powerful and not too involved solution is made is very interesting, I'm sure.
See also eigenvalues and electronics and bwise applications and examples for an example on what logical functions can act as building block for remembering the state, this page has the same block and the bwise code:
http://www.theover.org/Diary/ldiary6.html#bwise
This page is an example of how many bytes of source code Finite State Machines can be used to encode the number of states which often would fit in a byte, and the transitions could probably be coded pretty shortly as well. Then again, an assembly program is usually much bigger than the resulting object code.
I think after rereading the math notation is not all clear though things are overseeable, the first def line above means that the machine is defined by a function mapping of two variables to two new variables with certain domains and ranges. Actually the functions have ranges, they don't need variables added to hold the values, as in normal math. In fact, the only variable which is not a function argument is the state variable, which needs to be given an initial value. Though it is mathematically possible to define the machine as deriving its first 'stored' state from the initial input, or to define the state only after a cycle of the machine.
In the past I made a page with a special extension of the finite state machine concept, which you can try out on the web page through a javascript live animation:
http://www.theover.org/Tripod/Diary/diary62.html#machine
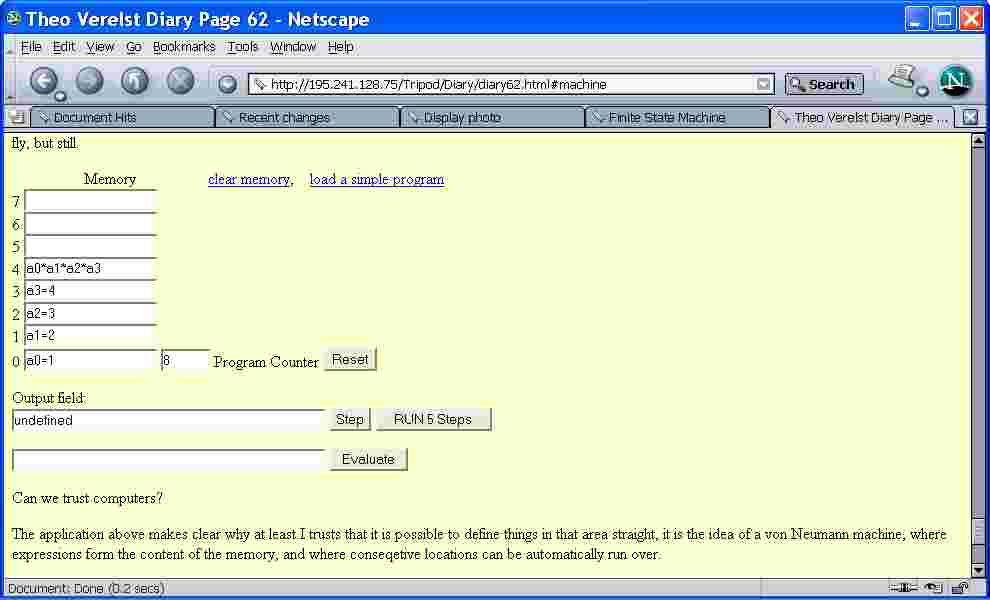
Of course on the tcl/tk wiki, one would at least have to give some code to make clear what a finite state machine can be made to tick like in tcl.
The following code makes the nextstate function by setting a array with a list of state, nextstate tuples, like a lookup table, initialized the state variable, and runs over some states. Next should be to include input, and then output. This of course is like a little program, easy enough, though quite fundamental, and interesting enough in terms of the possible traces, depending on the statespace, or domain and range of the nextstate function and the initial state. Ask dice players whether that is important.
array set nextstate {{} 1 1 2 2 3 3 inf}
proc compute_nextstate {oldstate} {
global nextstate;
puts "state $oldstate --> [set newstate $nextstate($oldstate)]";
return $newstate
}
compute_nextstate [compute_nextstate [compute_nextstate [compute_nextstate {}]]]this gives:
state --> 1 state 1 --> 2 state 2 --> 3 state 3 --> inf
Interesting for programmers here is of course is that we have an implicit state variable, the return value of the compute_nextstate function and the initial literal state value.
To list the State Transition Table in a listbox easily (assuming space in the tk toplevel . window):
pack [listbox .lb]
foreach {i j} [array get nextstate] {.lb insert end [list $i $j] }TV: I didn't realy finish the graphics idea yet. I'm starting a page on process algebra before that.
elfring 2004-02-22: There are relationships to switching networks and grammatical analysis. Do not forget the handling of stacks or buffers with FSMs...
I am interested in this design question: The execution of transitions [L1 ] can cause errors or throw exceptions. I expect that this will lead to new states. But my knowledge is so far that a transition leads to a predefined state and not to an unexpected new one. How are such situations modelled and designed with Petri nets or diagrams/graphs for finite state machines?
xnfec: 2012-03-07: Years ago I came across a multi language framework for developing FSMs called Libero. It was written by a company called Imatix and had a wacky newsletter too for a while until they got sensible. It even had a GUI written in VB3 - no tcl though. It's free and the code is available still: http://www.cs.vu.nl/~eliens/documents/libero/index.htm if any one wants to give it a try, its probably made for tcl/tk.