Monster Prime Predicting Formula
Monster Prime Predicting Formula
Many thanks to Gold for bringing this formula to my attention—
=====
gold31jan2018. Gauss-Legendre functions for number of primes has been loaded (c. 2017-05-28) in pending distribution of TCLLIB. Maybe coincidence, but sequence {7 11 13 14 } has been found on Sumerian tablet AO8862. Oeis {7 11 13 14} cited sequence property as Numbers n such that 16n+15 is prime. Tablet YBC10722 uses the input quantity 15 with the sequence {7 11 13 14}! Maybe your program could be used as example or exercise of the prime related functions in the TCLLIB.
16 * m + 15 — an amazing formula!!
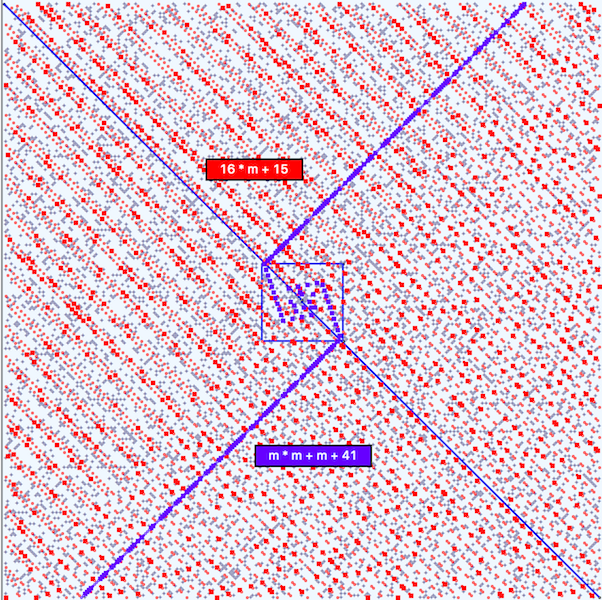
I’ve seen references to this formula in the past, but have been focused on what I’ve thought of as Prime Predictive Formulae, those which produce Prime Rich trajectories along Ulam Spirals. In my way of thinking, an important aspect of any such formula was it’s Potency, that is the ratio of predicted primes to the total number of predictions that a formula gave. Thus, for instance, Euler’s formula y = m² + m + 41 when applied to the set of all Primes Less Than 500K (PLT500K), yields 433 primes out of 706 predictions, for a potency of .394, which seemed pretty good.
For the same data set, (PLT500K), the above formula, 16 * m + 15 predicts 5197 Primes out of 31236 predictions, for a potency of 0.166. Although the Potency is not great, the fact that it calculates over 10 times as many primes is astounding and to my way of thinking, makes this simple equation Monstrously Prime Predictive.
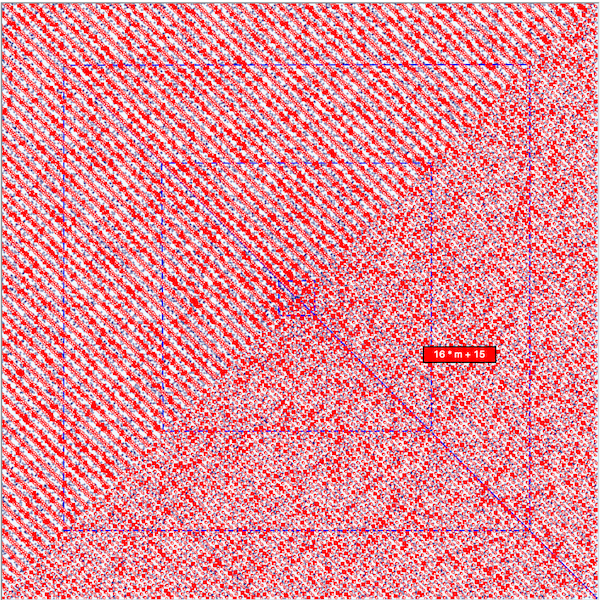
The following figure shows what these prime numbers look like on the Ulam Square Grid. The red squares represent Prime numbers and the small red circles are the non primes that the formula produces. If one draws a line through the center, from the lower left corner to the upper right corner, it appears that the upper left portion of the plot contains many more primes than does the lower right portion. This is very puzzling and seems to be somewhat analogous to the notion of Prime Rich directions, order where one might expect randomness.
The next figure is plotted on the smaller set of Primes, those Less Than 100K (PLT100K). In this case, the formula makes 6238 predictions with 1197 primes. Each red square is a prime number and the non primes are little red circles. Other Prime numbers are plotted as little blue + marks. Here the prime rich directions seem to be parallel to the Principle Axes. Euler’s formula is overlaid on the plot.
Now that we’ve introduced Triangular Ulam Spirals, Primal Screens— Part Two, we can see what our formula looks like in that system. The following figure shows the results of the formula for the (PLT500K) data set. Because of the different Spiral system, the numbers are a bit different: 5114 Primes are found out of 30657 predictions, for a potency of 0.166.
At first, it is puzzling why such a simple formula should predict so many prime numbers. I think the key to this is in the number of Predictions that a formula makes. In the Primal Screens Part two paper, we ended with a plot of two Formulae which predict empty trajectories— m * (m+1) / 2 and y = 2 * m * m + 2. The first formula yielded 988 predictions, the second 494.
If we think of a formula as a comb with many irregularly spaced teeth, then as the comb is placed over the line of positive integers, the teeth touch on integers at various locations. Some locations are Prime Numbers, others are non prime. The number of predictions depends on the Fineness of the spacing of the teeth. The first formula above has almost twice as many teeth as the second formula.
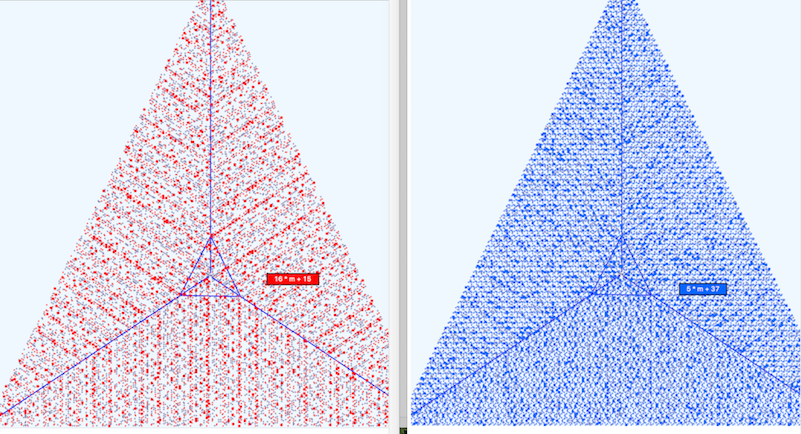
So, suppose we construct yet another formula: y = 5 * m + 37. There is nothing magical about this formula, it was just pulled out of thin air, but it represents a comb with even finer tooth spacing. Another way of saying this is that this formula walks through the number line more slowly and thus has a greater number of predictions. In fact, for the (PLT500K) data set, it makes 98100 predictions versus the 30657 predictions for our Amazing formula.
The following figure shows the two Triangular plots side by side for the (PLT100K) data set. Clearly the second formula has more predictions and finds more Primes.
The following table shows some of these results.
| Formulae showing various Predictions | |||
|---|---|---|---|
| Triangular System | For Primes Less Than 500K | ||
| Formulae | Predictions | Primes | Potency |
| Higher Predictions & Primes | |||
| 16M + 15 | 30657 | 5114 | 0.167 |
| 5M + 37 | 98100 | 10215 | 0.104 |
| Higher Potency | |||
| 2M² + 29 | 494 | 269 | 0.545 |
| 2M(M+7) - 59 | 490 | 240 | 0.490 |
| Low Potency | |||
| M(M+1)/2 | 988 | 1 | 0.001 |
| 2M² + 2 | 494 | 0 | 0.000 |
So, we see that the formula y = 16 * m + 15 isn’t really magical after all. There are many formulae which will produce large numbers of predictions and hence large numbers of Primes. The formula y = m of course will find all Primes but isn’t very interesting.
Again, many thanks to Gold for pointing this formula out to me.
I’m endebted to Arjen Markus, arjen for pointing me to the following Wikipedia page which has some additional (and amusing) information: https://en.wikipedia.org/wiki/Formula_for_primes
In that article, it states ‘In number theory, a formula for primes is a formula generating the prime numbers, exactly and without exception. No such formula which is efficiently computable is known.’
It seems that Euler and Lagrange were early practitioners of the practice.
I’ve been using the term Prime Predictive Formula in a different sense. The Formulae that I’ve been considering predict zero or more Prime Numbers. Formulae which predict Primes along Prime Rich directions have been my focus. My apologies to any Mathematicians that I may have offended.
See also:
Primal Screens, Primal Screens— Part Two and New Prime number Browser