Primal Screens— Part Two

A new way of doing Ulam Spirals

Welcome to part two of Primal Screens! In our previous note, Primal Screens, we displayed results from a TCL/TK package that plots the so called Ulam Spirals. See also [L1 ].

This installment is based around an hypothetical question — “Suppose Stanislaw Ulam had been carrying a pad of triangular graph paper rather than quadrille paper when he was trapped in his boring meeting?" Would he have still discovered lines of prime rich directions, or would he have just seen some random pattern? The short answer is 'Yes, he’d have seen prime rich directions on this different grid.’

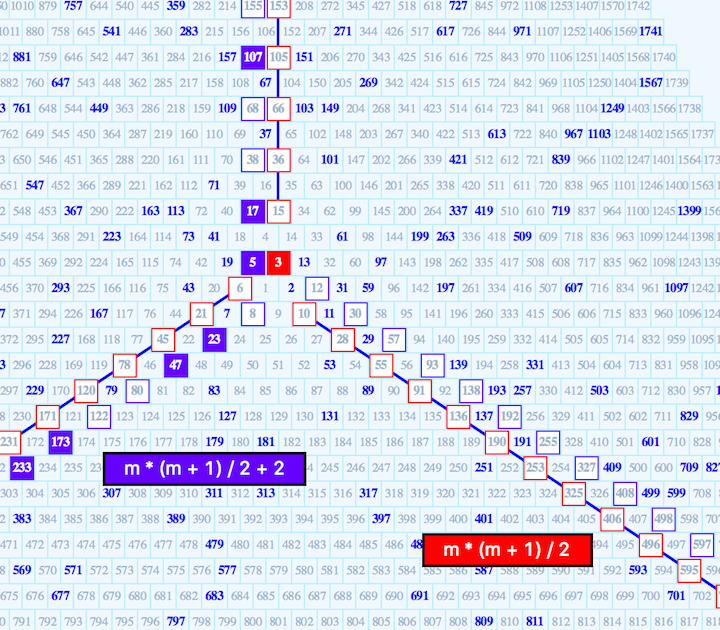
The following Triangular Grid system has been devised to explore this possibility. The basic Triangular Ulam Grid of integers appears thus:

PrSc2 #1

FIGURE 1

The integers in this scheme are laid out in a triangular, counter clockwise pattern. The basic trick, is to form an initial triangle of the first three integers, and then attach the line of integers 4, 5 and 6 downward along the upper left edge of that triangle, completing a larger triangle. Another line of integers is then added along the bottom edge of the larger triangle with integers 7, 8, 9 and 10, followed by a line to the right, going upward containing integers 11 thru 15. One then proceeds ad nauseum. Except for the integer 3, the final integer of each new strip is always a non prime. In the figure above, prime integers are in blue and bold, non primes are in italic and black or white. The black lines connect the final integers and these lines represent the Principle Axes in this system.

In the case of the Square Ulam Spirals, the Principle Axes were described by the formula y = m² . Initially, it was difficult trying to determine a formula for the Triangular Principle Axes. Fortunately Sloane’s On-Line Encyclopedia of Integer Sequences oeis.org came to the rescue. Feeding the final integers from above, 3, 6, 10, 15, 21, 28, 36, Sloane spit out the formula for Triangular Numbers — m*(m+1)/2.

The following figure shows a portion of the Coarse Triangular Grid with the Triangular Numbers plotted. Except for the integer 3, the rest of the integers are non-primes and are indicated by squares with red borders and numbers in gray. The formula for Triangular Numbers describes the Principle Axes in this system. In contrast to the Square Ulam Spirals, we see that the trajectory described by such a formula has three branches.

PrSc2 #2

FIGURE 2

In the previous note, we’d mentioned two ways of looking at Ulam Spirals— using a Coarse Grid or a Fine Grid. Figure 3 shows a portion of the Triangular Fine Grid for all primes which are less than 100,000. Here, the prime rich directions appear along lines that are antiparallel to the Principle Axes. In the Square System, the prime rich directions were parallel and perpendicular to the Principle Axes.

PrSc2 #3

FIGURE 3

To give a sense of scale, the blue triangle near the center represents the extent of the Coarse Grid, overlaid on the Fine Grid.

PrSc2 #4

FIGURE 4

As in the first paper, it’s possible to use the Coarse Grid to generate other prime predicting formulae by simple modifications of the Principle Axis formula y = m * (m + 1) / 2 . If we add the constant term 2, the new formula becomes y = m * (m + 1) / 2 + 2, and the integer sequence 3, 15, 36, 66, 105 along the vertical axis becomes 5, 17, 38, 68 etc. as seen in Figure 4. Here the primes are designated by blue squares with white numerals and non primes are white squares with blue borders. The Triangular Numbers again are indicated by the squares with red borders and numbers in gray.

Empty Channels Again

Looking closely back at Figure 3, we can see what look like empty channels going to the left and right, away from the center of the plot, just like the empty channels that appeared in the Square Ulam plots. It took a bit of experimenting to find the formulae for these channels, but the figure below on the left shows the formulas for the two horizontal trajectories as well as a third diagonal empty trajectory. It is interesting that the three branches of each trajectory are now collapsed into a single line. I have found no other instances where three branches collapse like this. In the Square Grid System, the two branches in formulae such as y = 4m² + 4m + 59 collapse into a single branch.

The figure on the right shows three branches of a trajectory in which all points but one are non prime.

PrSc2 #5

FIGURE 5

Spirals in both systems

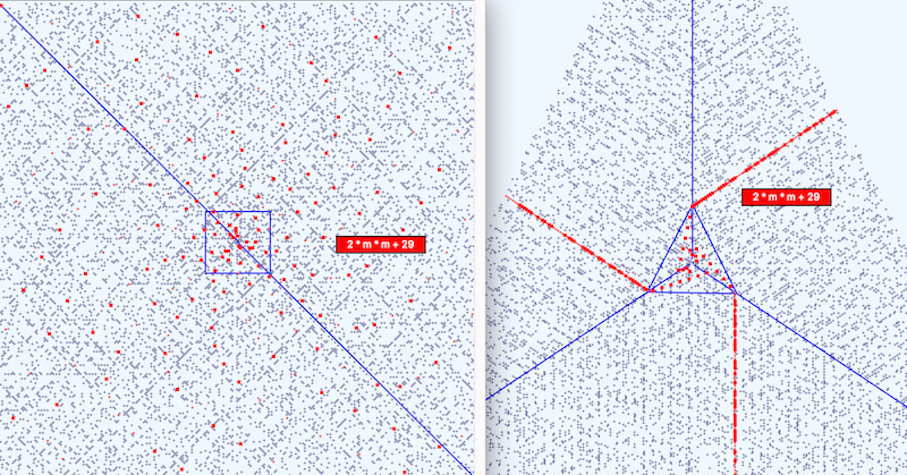
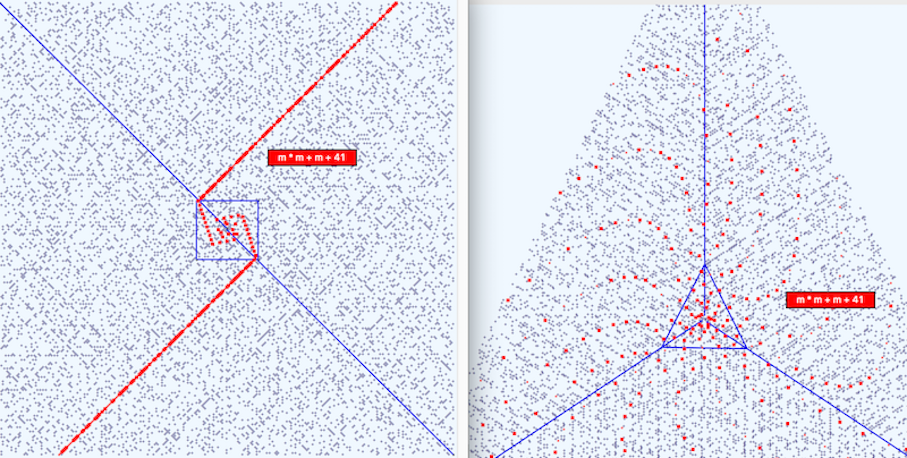
Formulas which show trajectories along prime rich directions in one system appear as spirals in the other system. Below we show the formula y = 2m² + 29 which in the previous paper was a spiral in the Square System. It now appears as a regular trajectory in the Triangular System. The next figure below shows Euler’s Trajectory in the Square and Triangular systems.

PrSc2 #6

FIGURE 6

PrSc2 #7

FIGURE 7

Larger Data Sets

PrSc2 #8

FIGURE 8

As in the Square Ulam paper, we’ve started looking at larger sets of Primes. The plot above shows a plot of all the Primes that are less than 500K. The 41538 Primes are all represented by a small black +. Four blue triangles overlay the plot. The first, inner Blue triangle is the limit of the Coarse grid, the next triangle encloses prime numbers less than 100,000, the third triangle is the limit of all prime numbers less than 300,000 and the last triangle contains all the primes less than 500,000.

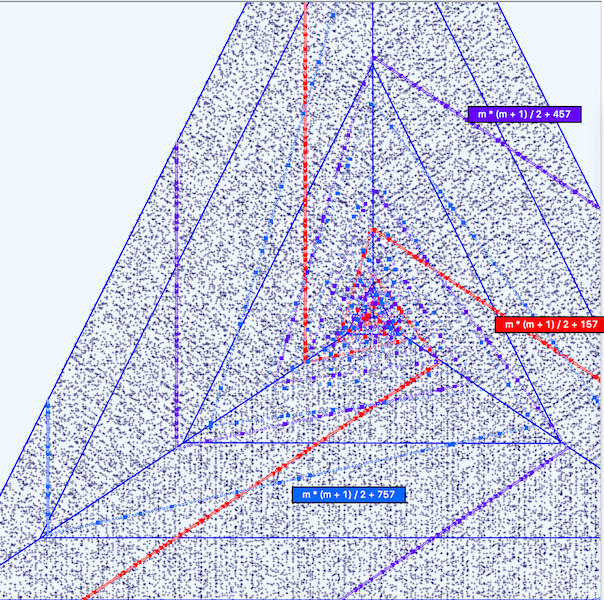
Three formulae are displayed in which the magnitude of the Constant term varies. The plot shows that bends in the trajectory branches occur further out as the constant term is increased. The plot also shows that bends occur as an individual branch crosses one of the fundamental axes, just as we had discovered with the Square system. Also, some portions along a branch are not parallel, anti-parallel or perpendicular to the principle axes.

Primes along a trajectory appear as the larger colored squares. Non Primes (barely visible at this resolution) are the small open circles with colored borders.

Had we limited our search to the primes less than100K, we’d have missed some of the bends from the formulae with 457 and 757 as constant terms.

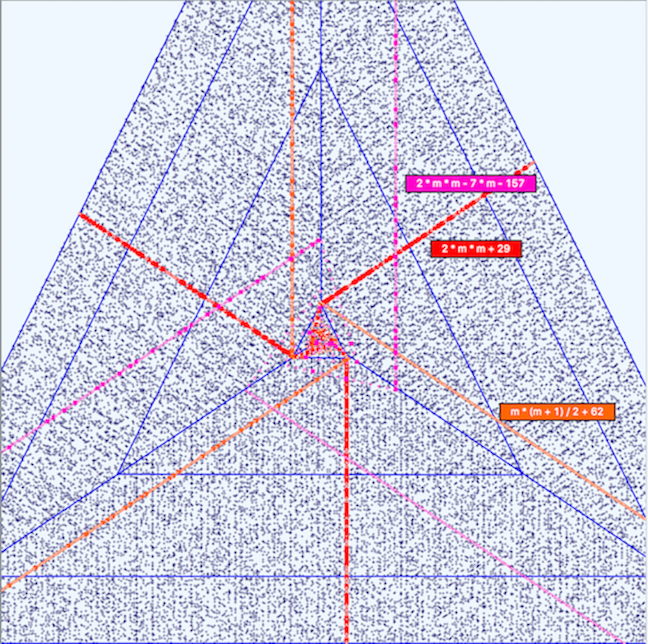
Other Kinds of Formulae

The following figure shows trajectories of three different formulae. The three branches of y = 2 * m * m + 29 are antiparallel to the principle axes. The other two formulae have branches which are parallel.

Note that all of the Triangular plots are truncated on the top and sides. Triangular images require more screen space than do Square images. The Browser has vertical and horizontal scrollbars that can be used to see those portions of an image that are cut off.

PrSc2 #9

FIGURE 9

Are Square Formulae more Potent than Triangular Formulae?

After many runs, it seems that Square Formulae have somewhat greater Potencies than do Triangular Formulae. The following table shows a few examples from the two systems. It is also interesting to see the various kinds of Formulae which produce Trajectories along Prime Rich Directions in both systems.

	Some Potencies in the Two Systems
Formulae	Predictions	Primes	Potency
Square System
M² - 79M + 1601	745	472	0.634
4M² - 2M + 41	352	216	0.614
M² - M + 41	706	433	0.613
36M² - 810M + 2753	128	76	0.594
M² - 1	705	1	0.001



Triangular System
2M² + 29	494	269	0.545
M(M+1)/2 + 457	988	203	0.205
M(M+1)/2 + 157	988	202	0.204
M(M+1)/2 + 757	988	144	0.146

M(M+1)/2	988	1	0.001
2M² + 2	494	0	0.000

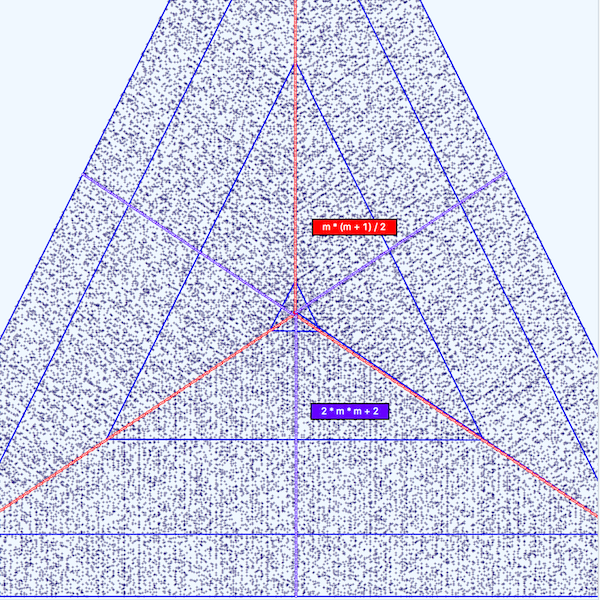
The last two Triangular Formulae which show mainly Empty Channels are depicted in the following Figure.

PrSc2 #10

FIGURE 10

The two trajectories are mirror images of one another. One trajectory is totally empty, the other has one prime. An interesting aspect of these two trajectories is that there are almost twice as many predictions for m * (m+1) / 2 as for y = 2 * m * m + 2. Hopefully this will be explained in Monster Prime Predicting Formula.

For the past 15 years I have worked on and off (mostly off) with Ulam Spirals. I’ve been mesmerized by their beauty and the many new aspects that have unexpectedly shown up over time. My hope is that others might find Ulam Spirals interesting also. Here’s to Stanislaw Ulam for his unexpected discovery.