Triangular Number Multiplication Study and demo example TCL calculator, numerical analysis
Triangular Number Multiplication Study and demo example TCL calculator, numerical analysis
This page is under development. Constructive Comments are welcome, but please load any constructive comments in the comments section at the bottom of the page. Please include your wiki MONIKER and date in your comment with the same courtesy that I will give you. Aside from your courtesy, your wiki MONIKER and date as a signature and minimal good faith of any internet post are the rules of this TCL-WIKI. Its very hard to reply reasonably without some background of the correspondent on his WIKI bio page. Thanks,gold15JUL2020
- Triangular Number Multiplication Study and demo example TCL calculator, numerical analysis
- Preface
- Introduction
- Outline Applications of Triangular Numbers
- Formulas of James_Whitbread_Lee_Glaisher, England, 1889
- Theorem of Nicomachus of Gerasa, c. 60 – c. 120 CE
- Table : Proof of Abu Al Karachi
- Formulas and Provisional Methods of Thomas Harriot, England, 1618
- Formulas and Provisional Methods of Joncourt, France ca. 1762
- Joncourt Methods on Squares
- Joncourt Methods on Cubes
- Quick Proc Fixes on Joncourt Methods
- Formulas of M. Arnaudeau, France ca. 1896
- Division with Triangular Numbers
- Conventional Identities with Triangular Numbers
- Developing Square Root Identities and Cubes from Triangular Numbers
- Gifts from the Song “ Twelve Days of Christmas
- Analogs to Volume of Boxes and Triangular Pyramids
- Cannonballs stacked into Pyramids
- BarTa Rectangle in the Babylonian math problems <draft>
- Push Button Operation
- Conclusions
- Table 1 : Triangular Numbers Study
- Table 2 : Proof of Abu Al Karachi
- Table 3 : Powers of 2 with added Modern Logarithm Notation
- Table 4 : Standard Multiplication Table
- Table 5 : Standard Multiplication Table, another
- Table 6 : Figurate Formulas and TCL Procs Table
- Testcases Section
- Screenshots Section
- figure 1. Calculator Screenshot
- figure 1b. Calculator Screenshot
- figure 2.Triangular Number chart
- figure 3. Favorite
- figure 4. Triangular Numbers in box
- figure 5a. Sum successive TN(S) and get square.
- figure 5a'. Checker Board Random Colors
- figure 5b. Sum successive TN(S) and get square of 4 coins.
- figure 5c. Sum successive TN(S) and get square
- figure 5d. Sum successive TN(S) on small checker board
- figure 5e. Sum successive TN(S) on checker board n**2=36
- figure 5f. Sum successive TN(S) on checker board
- figure 6. Euclid Multiplication proof?
- figure 7.Overshoot and Undershoot Coins
- figure 8.Coins Placed inside Circle
- figure 9.Second Try for Coins inside Circle
- figure 10. Pascal's Triangle
- figure 11. Pascal's Triangle Spreadsheet
- figure 12. Nicomachus Music Triangle Spreadsheet
- figure 13. Stacking Cannonballs use Triangular Numbers
- References:
- Pseudocode & Equations Section
- Appendix Code
- Hidden Comments Section
Preface
gold Here is some TCL scripts on the triangular number study. In reference to modern mathematics, the triangular number and modern extensions fall under the broad umbrella of the binomial theorem and algebra. Aside from the TCL calculator shell or graphics user interface gui, separate console programs were developed to dump the tables and check the algorithms as independent TCL procedures. Npte: Some tickets are closed and functions available in Tcllib. Many thanks to arjen & Andreas Kupries for the heavy lifting.
Introduction
The triangular numbers have the amazing property of multiplication in formulas using addition and and subtraction of Triangular Numbers TN. The published formulas have been adapted for the creation of multiplication products, squares, cubes, finding square roots, and division by reciprocal multiplication. The formulas for Triangular Numbers can be expressed typically either as the sum of 1,2, or 3 triangular numbers or as the polynomial functions f(n) or f(n,m). The original theorems were based on word formulas and integers only, more complicated in Greek, Latin, and Arabic manuscripts in the originals. However, many of the early methods and word forms using integers have been converted into modern math formulas, polynomial functions, or symbolic notation for the TCL computer code. For the TCL calculator, the formulas were fitted into TCL floating point fp. routines. Some testcases were developed using the available choose function in the TCLLIB math library, namespace export choose and <tcllib> ::math::choose returns the binomial coefficient C(n,k) = n!/k!(n-k)!
gold Draft. Figurate numbers are a type of mathematical sequence that can be represented geometrically. These numbers can be arranged in the form of regular, geometrical shapes or patterns, hence the term "figurate." Each figurate number corresponds to the number of points that can be arranged to form a specific geometric shape. Some common examples of figurate numbers include triangular numbers, square numbers, pentagonal numbers, hexagonal numbers, and so on. Triangular numbers, for instance, can be represented as equilateral triangles, where each successive number adds an additional row of points to form a larger triangle. Figurate numbers have various applications in mathematics, including number theory, combinatorics, and geometry. Figurate numbers can also be used to solve problems related to patterns, sequences, and geometric arrangements. Overall, figurate numbers provide a visual and intuitive way to understand and explore mathematical concepts.
gold 8/02/2020. I am shuffling some materials and reusing this older page. Unfortunately, the XXX network etc is blocking my access to this TCL WIKI page, TCLLIB, SourceForge, ActiveState, and other TCL download sites, open science materials and references etc. So the wiki prose is "catch can".
Outline Applications of Triangular Numbers
- 1) A fully connected network of n computing devices
- 2) tournament that uses a round-robin group stage of n teams
- 3) handshake problem, there are n players each have n-1 handshakes.
- 4) number ways can you pick two objects out of a set of n objects
- 5) find the binomial coefficient of choose (n+1,2)
- 6) finding a square, n**2 = TN(n) + TN(n-1)
- 7) finding a cube, n**3 = T(n) - T(n-1) = (n**2) * < n**2 +2*n +1 -n**2 +2*n - 1 )> /4, Theorem of Nicomachus of Gerasa,
- 8) multiplication product, m*n = T(m+n) - T(m) - T(n) ;# derivation by Dr. Mulatu Lemma, Savannah State university
- 9) T(m*n)= T(m)*T(n)+T(m-1)*T(n-1) ;# triangular number product law from David Radcliffe
- 10) Combinatorics, Ref. Variant construction from theoretical foundation to applications,Jeffrey Zheng,Yunnan University,China
- 11) Stacking cannonballs into stable pyramids, mathematician Thomas Herriot in 1587 and astronomer J. Kepler in 1611.
- 12) Network mesh connections in telegraph lines, roads, rails, subways, and canals
- 13) Number of legal ways to insert a pair of parentheses in a string of n letters, no adjacent back to back parentheses. credit N. J. A. Sloane, OEIS A000217
- 14) Find the grand total of gifts from the song “ Twelve Days of Christmas” using Triangular Numbers, and guest staring Tetrahedral Numbers TETN.
If there are 25 electronic devices in a mesh network, the total number of links would be the Triangular Number TN(n-1).TN(24) = expr { .5*($n*($n+1)}, general expression. TN(24) = expr { .5*(24*(24+1))} = 300
If there is a party of “n” members, the total number of handshakes would be the Triangular Number TN(n-1). For 7 members, the number of handshakes would be TN(6) = expr { .5*($n*($n+1)}, general expression. TN(6) = expr { .5*(6*(6+1))} = 21.
If there are “n” cities for a mesh network, then the number of roads that are needed would be the Triangular Number TN(n-1). For 6 cities, the number of roads would be TN(5) = expr { .5*($n*($n+1)}, general expression. TN(5) = expr { .5*(5*(5+1))} = 15
Find a square using Triangular Number TN’s. The square of 1000000 would be n**2 = T(n-1)+T(n), evaluation as n**2 = T(999999)+T(1000000). n**2 = expr (499999500000 + 500000500000} =1000000000000. n**2 = 1E12. For the square of 1E6 as n**2, the math check is multiply exponent by 2 for a square, expr {6*2} -> 12.
Find a cube using Triangular Number TN’s. The cube of 1000000 For example , r**3 = (T(n))**2- (T(n-1))**2, r**3 = (T(1000000))**2- (T(999999))**2, expr {500000500000**2-499999500000**2 } = 1E18. For the cube of 1E6 as r**3, the math check is multiply exponent by 3 for a cube, expr {6*3} -> 18.
Multiply 3*2 using Triangular Numbers. The Mulatu formula for positive integers is m*n = T(m+n) - T(m) - T(n). Subbing, m*n = 3 * 2 = T(3+2) - T(3) - T(2). From the Triangular Number tables, the product m*n = 15 - 6 - 3 = 15-9 = 6. The math check for the TCL console is expr { 2 * 3 } -> 6.
Find the number of legal ways to insert a non-adjacent pair of parentheses in a string of n elements. Number of legal ways is triangular number TN(3) = 6. There are 6 ways for three elements with 2 non-adjacent parentheses : (a)bc, (ab)c, (abc), a(b)c, a(bc), ab(c).
Find the daily number of gifts and grand total of gifts from the song “ Twelve Days of Christmas” using Triangular Numbers, and guest staring Tetrahedral Numbers TETN and Triangular Pyramids. Each subtotal for a day’s gifts is a Triangular Number TN. The gifts from Total_Twelve_Days is expr { TN(1)+TN(2)+TN(3)+TN(4)+TN(5)+TN(6)+TN(7)+TN(8)+TN(9)+TN(10) +TN(11) +TN(12) }. The TCL expression is expr {1 + 3 + 6 + 10 + 15 + 21+ 28 + 36 + 45 + 55 + 66 + 78 } = 364 gifts. The quick answer is that the Tetrahedral Number TETN has the formula (n+(n+1)+(n+2))/6. TETN(12) = expr {($n*($n+1)*($n+2))/6. } = expr {(12*(12+1)*(12+2))/6. } = 364 gifts.
Symbolic Differentiation in TCL expression in x may be of interest. symdiff { ($x*$x + $x)*.5 } x -> ((($x + $x) + 1.0) * .5).
proc tnd {x} {return [ expr { ((($x + $x) + 1.0) * .5)}]} Formulas of James_Whitbread_Lee_Glaisher, England, 1889
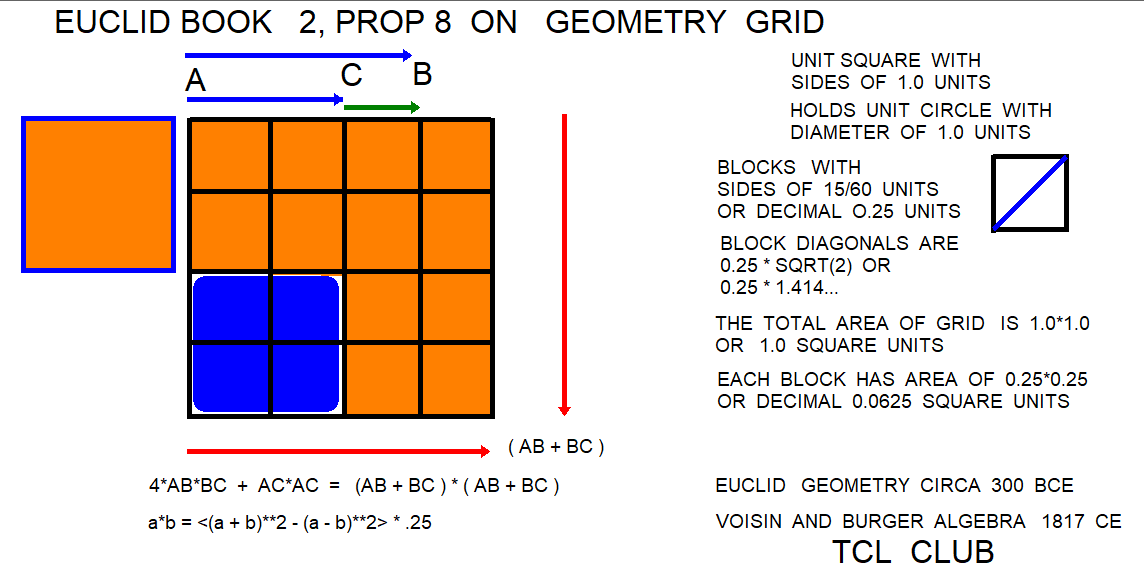
From the modern derivations and formula extensions, there are a number of formulas that can be presented into TCL code. The modern extension to the multiplication algorithm from the binomial theorem is a*b = 0.5*{a+b)**2 -a**2-b**2}. A triangular number can be presented as choose (N 2) or math::choose (n+1 2) can be expressed as (n+1)!/ (n+1−2)!2!. Simplifies to n(n+1)/2. However, many of the early methods or formulas must converted into a formula or symbolic notation for the TCL computer code. The Binomial Theorem in Euclid II, 4, is formulated as (a + b)**2 = a**2 + 2ab+ b**2, Pascal triangle coefficients <1 2 1>. Some formulas were early published by Elie de Joncourt, 1762, Netherlands. The triangular number TN = N*(N+1)/2. The sum of consecutive TN numbers are squares. TN <aa> + TN <aa+1> = square number. Joncourt used TN to calculate square roots and cube roots. Joncourt used formula as aa * bb = <(aa+bb)**2 -aa**2 -bb**2>/2. The key term is <(aa+bb)**2 -aa**2 -bb**2>, which is twice answer. The Binomial theorem is formulated as a*b = 0.5*{(a+b)**2 -a**2-b**2}. The ground breaking formula for triangular numbers was published widely from mathematician James Glaisher, as near as I can tell. James Glaisher published the triangular numbers TN formula in 1889. Triangular multiplication is formulated as aa * bb = TN <aa-1> + TN <bb> - TN <aa-bb-1>. The Glaisher formula returns the triangular multiplication product as an integer from two natural numbers. James Glaisher discussed TN and Quarter Square variants in his original papers. The conventional formula for Quarter Squares is a*b = <(a + b)**2 − (a − b)**2> * .25
The Glaisher formula returns the triangular multiplication product as an integer from two positive natural numbers. Triangular multiplication is formulated as aa * bb = TN <aa-1> + TN <bb> - TN <aa-bb-1>. The Glaisher formula is discussed as a factorial expression of n * (n-1) in the second order. The Glaisher formula does not define the Triangular Number for negative numbers. As understood here, the term TN <aa-bb-1> might return negative numbers for bb > aa, so suggest swap or reorder to avoid TN < -r >.
- T(n)= 1 + 2 + 3 ... n = n * (n + 1 ) / 2. ;# explanation in similar notation
- ab = (1/2) * (a -r) * a + (1/2) * b * (b + r) -n * (a - b -r) * (a - b) ;# derivation, from one of Glaisher reprints,r=?1,n=?(1/2)
- ab = (1/2) * (a-1) *a + (1/2) * (b+1) *b - (1/2) * (a-b-1 ) *(a-b ) ;# derivation, constraints below on a and b
- TN <aa-1> = (1/2) * (a-1) *a ;# derivation, first substitution term
- TN <bb> = (1/2) * (b+1) *b ;# derivation, second substitution term
- TN <aa-bb-1> = (1/2) * (a-b-1 ) *(a-b ) ;# derivation, third substitution term
- aa * bb = TN <aa-1> + TN <bb> - TN <aa-bb-1> ;# Glaisher formula for Triangular Number product
Theorem of Nicomachus of Gerasa, c. 60 – c. 120 CE
- proof on Nicomachus theorem from post of Jacques Distler, 13Jul2003
- T(n) = 1 + 2 + 3 + 4 ... = n*(n+1)/2
- T(n) is area of right angle triangle of sides n and n+1
- T(n)**2 = <(n**2)*(n+1)**2> / 4
- T(n) - T(n-1) = (n**2)*<(n+1)**2 - (n-1)**2 > /4
- T(n) - T(n-1) = (n**2) * < n**2 +2*n +1 -n**2 +2*n - 1 )> /4 = n**3
- T(n) - T(n-1) = n**3
Table : Proof of Abu Al Karachi
related formula 1**3 + 2**3 + 3**3 ... + N**3 = ( 1 + 2 + 3 ... + n)**2
| table 2 | printed in | TCL format | |
|---|---|---|---|
| expression | answer | comment, if any | |
| expr { 1 } | ;# -> 1 | ||
| expr { 1 + 2 } | ;# -> 3 | ||
| expr { 1 + 2 + 3 } | ;# -> 6 | ||
| expr { 1 + 2 + 3 + 4 } | ;# -> 10 | ||
| expr { 1 + 2 + 3 + 4 + 5 } | ;# -> 15 | ||
| expr { 1**3 } | ;# -> 1 | ||
| expr { 1**3 + 2**3 + } | ;# -> 9 | ||
| expr { 1**3 + 2**3 + 3**3 } | ;# -> 36 | ||
| expr { 1**3 + 2**3 + 3**3 + 4**3} | ;# -> 100 | ||
| expr { 1**3 + 2**3 + 3**3 + 4**3 + 5**3 } | ;# -> 225 |
Formulas and Provisional Methods of Thomas Harriot, England, 1618
The manuscript of Thomas Harriot suggests some interest in solving sum of cubes and some general cubes with Triangular Numbers. As the proof in Table 2 ref Abu Al Karachi in 1100 CE suggests, this cubic method was probably not original with Harriot. For example in using the TCL calculator, r**3 = (T(n))**2- (T(n-1))**2, r**3 = (T(100))**2- (T(99))**2, expr {5050**2-4950**2 } = 1E6, cube of 100 as r. For example in using the TCL calculator, r**3 = (T(n))**2- (T(n-1))**2, r**3 = (T(1000000))**2- (T(999999))**2, expr {500000500000**2-499999500000**2 } = 1E18, cube of 1E6 as r. Not sure the cubic method here applies to all n, or all cubes, or n < 2. Also one could use the Glaisher formula as aa * aa = TN <aa-1> + TN <aa> - TN <aa-aa-1> for squaring the numbers in a proc.
Formulas and Provisional Methods of Joncourt, France ca. 1762
It is reported that Joncourt used his table for finding squares, square roots, and cubic roots. For testing provisional methods, the TCL triangular number calculator may be used to develop testcases, rather than the table that Joncourt used. From the identity, the square of 5 would be the sum of successive triangular numbers as n**2 = T(n-1)+T(n), evaluation as n**2 = T(4)+T(5), from the TCL calculator n**2 = 10 + 15, n**2 = 25. The square of 100 would be n**2 = T(n-1)+T(n), evaluation as n**2 = T(99)+T(100), from the TCL calculator n**2 = 4950 + 5050, n**2 = 10000. The square of 1000000 would be n**2 = T(n-1)+T(n), evaluation as n**2 = T(999999)+T(1000000), from the TCL calculator n**2 = 499999500000 + 500000500000, n**2 = 1E12'. The Joncourt method for finding squares with triangular numbers appears to be exact answers. The Joncourt method for squares could easily be written as a proc in the calculator.
- S(n) + S(n+1) = (n + 1)**2 ;# Equivalent Joncourt method for squares in similar notation
- S(n) + S(n+1) = (1/2)* (n*(n + 1) + (n + 1)*(n + 2)) ;# Equivalent Joncourt method for squares in similar notation
proc joncourt_sq {n} {return [ expr { (1./2)* (( $n *( $n + 1)) + ( $n + 1)*( $n + 2) )}]} ;# Equivalent Joncourt method for squares in similar notation
;# Usage joncourt_sq 1 -> 4 ;# tricky, but entering 1 as n with 2 as implied (n+1) returns 4, correct
;# note >> I'd use (n-1) myself, but I was not in charge 260 years ago.
;# proc oblong_number {n} {return [ expr { $n * ( $n + 1) }]} ;# Comparison in similar notation
;# proc whats_it {n} {return [ expr { $n * ( $n - 1) }]} ;# Comparison in similar notation, n > 1Joncourt Methods on Squares
The reported Joncourt methods for square roots and cube roots include both exact formulas and more approximation formulas. sqrt(n) =~ inverse T((1/2)*n), ~ inverse T((1/2)*25), ~ inverse T(14.5) rounded up,~ inverse T(15)=5, sqrt(n) = 5. More precisely, the Joncourt methods could be used to give a lower and upper bound for the square root. In this case and if not exact, the square root would be between ~ inverse T(10) and ~ inverse T(15), between 4 and 5.
A TCL procedure was developed for the inverse triangular number as m. The general definition is triangular number m = n*(n+1)*.5 . Multiply both terms by 2 and rearrange terms, it was found that 2*m=n*(n+1). So the square root of 2*m is between n and (n+1) by the original definition. The TCL procedure in three steps is 1) multiply m by 2, 2) take square root, and 3) round down to nearest whole in the TCL expressions, int or floor. In a similar manner, the next triangular number (m+1) can be found either by adding 1 to m or by rounding up in the TCL expression, ceil. These two TCL procedures are very useful in following the Joncourt methods. Note that Joncourt was using the triangular number tables, not computer programs. But not all numbers are triangular numbers in strict definition. If m is 1) either not a triangular number to start or 2) a number in floating point with mantissa, these TCL procedures return the natural number pairs n and (n+1) that generate the triangular number pairs that bracket m with lower and upper triangular numbers.
- definition is triangular number m = n*(n+1)*.5
- 2*m=n*(n+1), sqrt of 2*m is between n and (n+1)
- trivial case for 0, m=0, 0 * 2 = 0, sqrt (0) = 0 , int ( 0 ) = 0
- trivial case for 1, m=1, 1 * 2 = 2, sqrt (2) = 1.414 , int (1.414 ) = 1, Next number (m+1)= ceil ( 1.414 ) = 2.
- m=55, 55*2=110, sqrt ( 110 ) = 10.4, floor (10.4) = 10. Next number (m+1)= ceil ( 10.4 ) = 11.
- m=1641157986, 1641157986 * 2=3282315972, sqrt ( 3282315972 ) = 57291.499, floor (57291.499) = 57291. Next number (m+1)= ceil ( 57291.499) = 57292.
proc inverse_triangular5 { m } { return [expr { floor (sqrt (2.*$m)) }] }
;# Usage inverse_triangular5 0 -> 0
;# Usage inverse_triangular5 1 -> 1
;# Usage inverse_triangular5 1641157986. -> 57291.0
;# inverse_triangular5 1641157986.999 -> 57291.0
proc inverse_next_triangular5 { m } { return [expr { ceil (sqrt (2.*$m)) }] }
;# Usage inverse_next_triangular5 1641157986. -> 57292.0
;# Usage inverse_next_triangular5 1641157986.999 -> 57292.0
;# find square root of number, if exact or perfect square (n*n), not all numbers work
proc sqrt_triangular5 { m } { return [ inverse_triangular5 [* $m .5 ] ] }
;# Usage sqrt_triangular5 9 -> 3.0
;# Usage sqrt_triangular5 121 -> 11.0
;# Usage sqrt_triangular5 10000 -> 100.
;# Usage sqrt_triangular5 3282258681 -> 57291.0- find square root of triangular number 3282258681 using Joncourt methods
- expr 3282258681*.5 = 1641129340.5
- inverse_triangular5 1641129340.5 = 57291.0
- TCL check is expr 57291.**2 = 3282258681.0
- find square root of triangular number 3283175401 using Joncourt methods
- expr {3283175401*.5} = 1641587700.5
- root = inverse_triangular5 1641587700.5 = 57299.0
- TCL check is expr {57299 ** 2} = 3283175401
- study square root of non-triangular number 3282717041.0 using Joncourt methods
- expr {3282258681 + ( 3283175401- 3282258681 )*.5 -> 3282717041.0}
- expr {3282717041.0 * .5} -> 1641358520.5
- inverse_triangular5 1641358520.5 -> 57295.0
- inverse_next_triangular5 1641358520.5 -> 57296.0
- square root should be between 57295.0 & 57296.0
- check expr 3282717041.**.5 -> 57295.0001
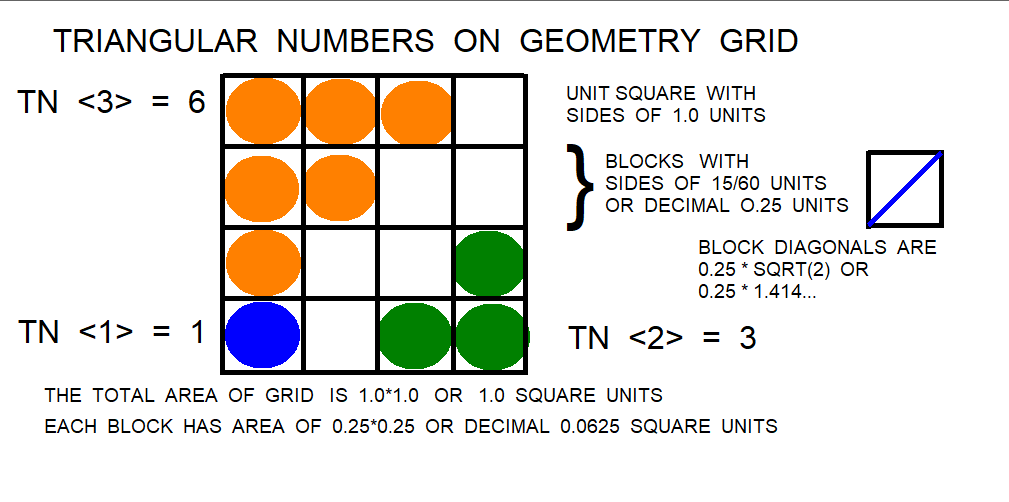
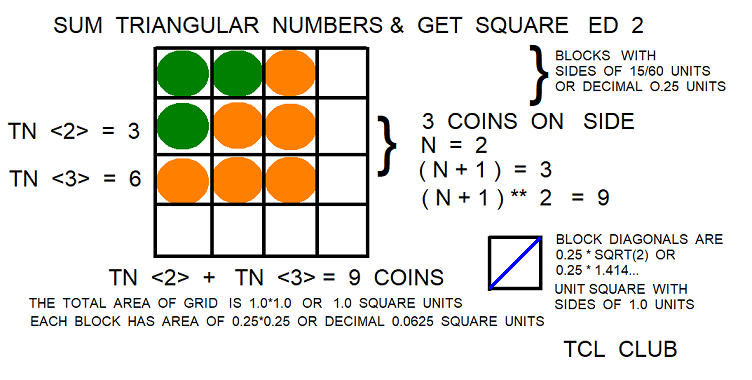
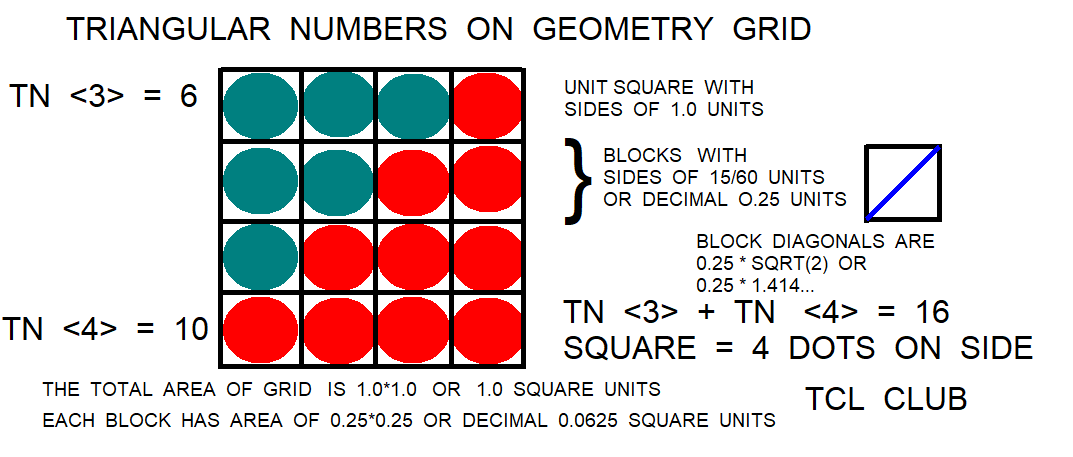
For some relief from abstract numbers, lets look at a graphical proof of the Joncourt square formulas, using coins in Figure 5. The desired square of (n+1)**2 is the sum of the 2 successive triangular numbers TNT(n) and TN(n+1). Refer to the graphical proof in Figure 5 : Sum successive TN(S) and Get Square. For the example of coins on a geometric grid in Figure 5, n=3, (n+1) = 4, TNT(3) = 6, and TN(4) = 10. In TCL expressions, the sum is expr { TNT($n) + TN($n+1) }, expr { 6 + 10 }, sum = 16. The square in Figure 5 has 16 coins total with each side of 4 coins. The TCL expression check is (n+1)**2, expr {4**2} = 16. Also check is 16**.5, expr {16**.5} = 4. Based on the Joncourt methods, the TCL procedure solve_sqrt 16 returns 4 coins. Joncourt’s point is that the methods and the same triangular numbers from the square can be used to develop the cube with his formula n**3=nn+2nt, in Joncourt notation
Continuing graphical proof of the Joncourt square formulas, the desired square of (n+1)**2 is the sum of the 2 successive triangular numbers TNT(n) and TN(n+1). Another example of coins on a geometric grid, n=1, (n+1) = 2, TNT(1) = 1, and TN(2) = 3. In TCL expressions, the sum is expr { TNT($n) + TN($n+1) }, expr { 1 + 3 }, sum = 4. The graphic square has 4 coins total with each side of 2 coins. The check in TCL expressions is the square = expr { ($n+1)**2 } = expr { 2 **2 }, square = 4 coins. Based on the Joncourt methods, the TCL procedure solve_sqrt 4 returns 2 coins. A second example of coins on a geometric grid, n= 2, (n+1) = 3, TNT(2) = 3, and TN(3) = 6. In TCL expressions, the sum is expr { TNT($n) + TN($n+1) }, expr { 3 + 6 }, sum = 9 coins. The graphic square has 9 coins total with each side of 3 coins. The check in TCL expressions is the square = expr { ($n+1)**2 }, expr { 3 **2 }, square = 9 coins.
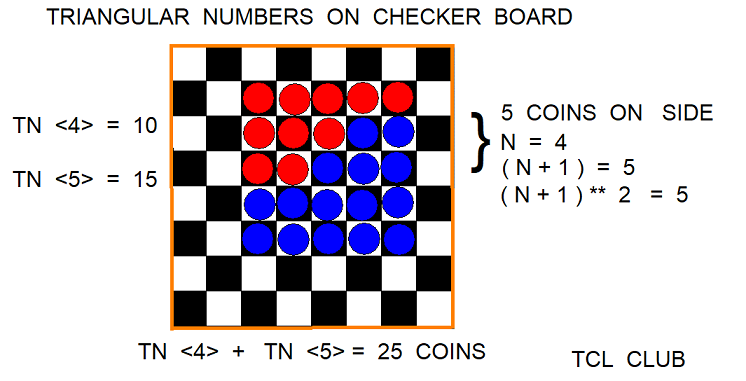
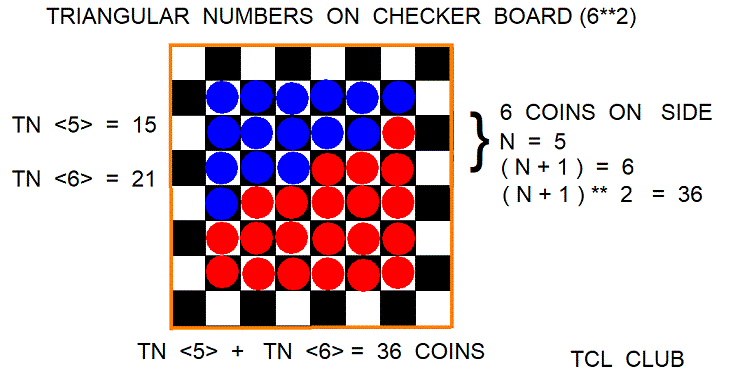
Lets place 64 coins on a checker board using the Joncourt methods for triangular numbers. The Joncourt rules are the sum of the 2 successive triangular numbers TNT(n) and TN(n+1) equals a square of 64 coins. Another Joncourt rule is that (n+1)**2 in the larger triangular number equals 64. Further on the Joncourt rules, since the sum of the two triangular numbers equals 64, TN =~ expr { 64 * .5 } or 32 coins. By inspection of the line items on the Joncourt table, 32 should lie between two triangular numbers, which are using the inverses, 28 = TNT(7) and 36 = TN(8). As a check, since n = 7 and (n+1) = 8, then the TCL check expression is expr { ($n+1)**2 } = expr { (7+1)**2 } = 64'.
The ratio of terms in the series of triangular numbers, T(n-1) over T(n), approaches 1:1 at infinity. If looks at the larger TN ratios along the diagonal in the figures with a squint eye, one can see the two sets of coins as two <two equal sides> triangles and somewhat equal areas in the larger squares, comprising squares in figures 5c and 5d .
- Joncourt Square Example 1 : n=160345.0 TN = 12855339685. T(160344)= 12855179340.0 , expr 12855339685+12855179340.0 = 25710519025.0 The desired square of 160345.0 is the sum of the 2 successive triangular numbers TN(160345) and TN(160344). The TCL expression check is expr {160345**2} = 25710519025.
- Joncourt Square Example 2 : square = 25710519025.square = TN(n) + TN(n+1).square root =~ inverse (expr 25710519025./2 ) = 12855259512.5. inverse_tn 12855259512.5 -> 160344.5. The TCL expression check is expr {160345**2} = 25710519025.
- Square Example 3: n = 17854.0,'TN( 17854)=T=159391585.0, TN( 17853)=t=159373731.0, nn= expr 159391585.0+159373731.0 = 318765316.0. The TCL expression check is expr {17854**2} = 318765316.
- Square Example 4: n=19467.0, TN(19467)=T=189491778, TN(19466)=t=189472311, nn= expr 189491778+189472311.0 = 378964089. The TCL expression check is expr {19467**2} = 378964089.
49 coins
expr { 49/2. } -> 24.5
from Joncourt table, inverse TNI(21) = 6
from Joncourt table, inverse TNI(28) = 7
24.5 between 21 and 28
sqrt (49) between 6 and 7.Joncourt Methods on Cubes
For the approximate cube root method on 27, the crt(n) =~ inverse T((1/3)*n), ~ inverse T(10) rounded, concludes 3 <= crt(n) <= 4. For the approximate cube root method on 25, the crt(n) =~ inverse T((1/6)*n), ~ inverse T(4.16) rounded to inverse T(6), concludes 2 <= crt(n) <= 3. Other method uses the Abu al-Karaji proof or identity of 1**3+2**3+3**3...n**3 = (1+2+3...n)**2 or sigma(3)=sigma(1)**2. From Joncourt in Latin version as follows. With the formula TT-tt=n**3, the majority of numbers can be fitted. If the cube has 11 digits, then the first 8 digits are used. If the cube has 12 digits, then the first 9 digits are used. Effectively multiplication of n here is by 0.001.
The first Joncourt method for cubes is inspection on cube roots. For the approximate cube root method on 27, the crt(n) =~ T((1/3)*n), ~ inverse T(10) rounded, concludes 3 <= crt(n) <= 4. For the approximate cube root method on 25, the crt(n) =~ inverse T((1/6)*n), ~ inverse T(4.16) rounded to inverse T(6), concludes 2 <= crt(n) <= 3 .
The second Joncourt method or cubes uses the Abu al-Karaji proof or identity of 1**3+2**3+3**3...n**3 = (1+2+3...n)**2 or sigma(3)=sigma(1)**2 in modern notation. From Joncourt in Latin version as follows. With the formula for triangular pair numbers TN-TT=n**3, the majority of <triangular> numbers can be fitted into cubes <but not all numbers>. If the cube has 11 digits, then the first 8 digits are used. If the cube has 12 digits, then the first 9 digits are used. Effectively multiplication of n here is by 0.001. After the pair of successive triangular numbers are resolved, the radix or cubic root crt is normally the inverse of the lesser triangular number found in the table. Effectively the Joncourt method for cubes uses the pair of successive triangular numbers as the lower bound and upper bound for the cubic root. The cubic root is between the lower bound of the lesser triangular number TT and the greater bound of the greater triangular number TN. TT >= CRT <= TN
- Joncourt Cubic Example 1 : TN=20000, tt=19900, N**2 =3961000, tt=388129401, 7880599, cube=199. The TCL expression check is expr {199**3} = 7880599. fie 19900 = 7880599000000. fie 20000 = 8000000000000.
- Joncourt Cubic Example 2 : n=10,tt=3025,tt=2025, difference=1000. n*n=100,2nt=900, 2*10* , 900+100=1000. the difference n**3 is n*n+ 2*n*t .
- Joncourt Cubic Example 3 : n=20, tt=44100,TT=36100 & difference=8000. From the Joncourt formula n*n=400, and 2N*t =40*190=7600, 400+7600=8000. difference 8000 = n*n + 2*n*T. The TCL expression check is expr {20**3} = 8000. T(20)=210. T(19)=190 The formula is n*n + 2*n*T(lesser) equals difference of TT and tt . expr 210**2=44100, The TCL expression check is expr {190**2} = 36100
- Joncourt Cubic Example 4: If the cube has 11 digits, then the first 8 digits are used, from the Latin. n=29522282571, The greater TN is 29503629, The next lesser TN is number 29522282, The radix or root is 3091 from the inverse 4778686 in the Joncourt table. The TCL expression check is expr {3091**3} = 29532282571. The cubic root is equal to or between 3091 (n ) and 3092 (n+1). T(3091 )=4778686, T(3092)=4781778
- Joncourt Cubic Example 5: If the cube has 12 digits, then the first 9 digits are used, from the Latin. n=207054415296, The cube TN= 206425071, The next lesser TT is 207054415, n= 5916 from the Joncourt table. The TCL expression check is expr {5916**3} = 207054415296. The cubic root is equal to or between 5916 (n) and 5917 (n+1). T(5916)=17502486, T(5917)=17508403.
- Joncourt Cubic Example 6: n**3 = n*n+2*n*t, n = 160345 , expr 12855339685+12855179340.0+2*160345*12855179340, expr 12855339685+12855179340.0+2*160345*12855179340 = 4122553173063625.0. The TCL expression check is expr {160345**3} = 4122553173063625.
- Joncourt’s point is that the methods and the same triangular numbers from the square can be used to develop the cube with his formula n**3=nn+2nt, in Joncourt notation.
- derivation of cube root formula into conventional notation
- n**3=nn+2nt ;# Joncourt formula and his notation.
- cube(n) = TN(n) + TN(n-1) + 2*n*TN(n-1) ;# substitute triangular numbers TN(n) & TN(n-1)
- 2*n*TN(n-1) = cube(n) - TN(n) - TN(n-1), cube root n = <cube(n) - TN(n) - TN(n-1)> / (2*TN(n-1))
- ;# solve for cube root n, assuming exact formula for integers, not fp.
- cube root = expr (4122553173063625-12855339685-12855179340.0)/ (2.*12855179340)
- cube root = 160345.0
- The TCL expression check is expr {160345**3} = 4122553173063625
- Reusing numbers in above case for square. square = 25710519025. square = TN(n) + TN(n+1).square root =~ inverse (expr 25710519025./2 ) = 12855259512.5.inverse_tn 12855259512.5. 160344.50000077958. The TCL expression check is expr {160345**2} = 25710519025
Quick Proc Fixes on Joncourt Methods
;# quick proc fixes on Joncourt methods
;# TN = expr {$n*($n+1)/2} formula for triangular number TN
proc tn {n} {return [expr { $n*($n+1)/2}]} ;# formula for triangular number TN
proc tn_sq {n} {return [expr {($n*($n+1)/2)**2}]} ;# TN squared
;# Usage tn_sq 3 -> 36 tn_sq 13 -> 8281
;# 0, 1, 9, 36, 100, 225, 441, 784, 1296, 2025, 3025, 4356, 6084, 8281, ...
;# sequence A000537 in the OEIS
;# substitute ($n-1) for lesser term TN in difference of terms
proc diff_sq_TNS {n} {return [expr {($n*($n+1)/2)**2-(($n-1)*(($n-1)+1)/2)**2}]}
;# Usage diff_sq_TNS 5916 ;# -> 207054415296, difference of successive squared TN's = r**3
;# Example TN(2)=3 , TN(3)=6
;# TN(2)**2-TN(3)**2= (n+1)**3=27
;# check that expr {6**2-3**2} = 3**3 = 27
;# solution to quadratic equation with quadratic formula
;# for inverse triangular number
;# TN = $n*($n+1)/2 #; TN = ($n**2 + $n) /2 ;# N**2 + $n -2TN = 0, quadratic in $n
;# $n = ( -1 +- (1 + 8.* $TN )) /2. from quadratic formula
;# inverse triangular number in floating point
proc inverse_tn {tn } { return [ expr { (((1.+8*$tn)**.5)-1.)*.5 }]} ;# inverse triangular number
;# Usage inverse_tn 6 -> 3 inverse_tn 4778686 -> 3091.0 inverse_tn 4781778 -> 3092.0
;# inverse_tn 17502486 -> 5916.0 inverse_tn 17508403. -> 5917.0
;# could use int() for integers output, but keeping floating point fp. for now.
;# interested in fp. interpolation of square and cube roots using Joncourt tables.
;# another solution to quadratic equation
;# for inverse triangular number
;# TN= n*(n+1)/2 = (n**2+n)/2
;# completing the square gives
;# 2*TN = (n+(1/2))**2 - (1/4)
;# solving for n with $tn as constant
;# n = (2.*$tn + (1./4. ))**.5 - (1./2.)
proc inverse_TN_int {tn} { return [ expr {round((2.*$tn + (1./4. ))**.5 - (1./2.)) } ] }
;# Joncourt's approximate method is square divided by 2, then inverse TN
;# Usage example for square root of 121, expr {121/2.} = 60.5
;# Usage inverse_TN_int 60.5 -> 11
;# from the Joncourt table, TN(10)=55 <n>, TN(11) = 66 <n+1>
;# so 10 <= sqrt(121) <=11
;# Joncourt method for square root into TCL proc
;# S(n) + S(n+1) = (n + 1)**2 = n**2 +2*n +1
;# transform equation to quadratic equation in $n
;# n**2 +2*n + { 1 - (S(n) + S(n+1)) } = 0
;# quadratic formula = (-b +- sqrt( b**2 -4ac))/2a
;# (-2 +- sqrt( 2**2 -4*1*{ 1 - (S(n) + S(n+1)) }))/2
proc solve_sqrt {ttt} {return [ expr {((-2 + sqrt( 2**2 -4*1*( 1 - $ttt )))/2)+1} ] }
;# Usage solve_sqrt 49 -> 7.0 ; solve_sqrt 121 -> 11.0
;# Usage solve_sqrt 378964089 -> 19467
;# solve_sqrt 2 -> 1.4142135623730951 ;# works in floating point
;# But proc solve_sqrt {ttt} is test bed and not checked out in FP.
Formulas of M. Arnaudeau, France ca. 1896
The works of M. Arnaudeau on triangular numbers were largely manuscript and were never completely published, but a review article by Edward L. Stabler in 1897 gave many details of the planned work of M. Arnaudeau . Apparently, these formulas used a base of the binomial theorem (a+b)**2 = a**2 + b**2 + 2ab, or follow on to ab = (1/2) * ((a+b)**2 - a**2 - b**2 ), and then substitute the algebraic quantities on the right side with quantities from triangular numbers. The planned inclusion of the Arnaudeau reciprocal tables would have made it possible to use the tables of triangular numbers to perform divisions.
- S(n)= 1 + 2 + 3 ... n = n * (n + 1 ) / 2. ;# explanation in similar notation
- ab = S(a) + S(b-1) - S(a-b) ;# constraints below on a and b
- ab = S(a-1) + S(b) - S(a-b-1)
- ab = S(a-n) + S(b+n-1) - S(a-b-n) - S(n-1) ;# for any n > 0
- ab = S((a-1)/2 +b) - S((a-1)/2 -b)
- ab = S((a/2)+b-1) - S((a/2)-b-1) + b
- ab = S(a+b) + S(a) - S(b)
Division with Triangular Numbers
The planned inclusion of the Arnaudeau reciprocal tables would have made it possible to use the tables of triangular numbers to perform divisions. Some identities have been collected and found in literature which might be useful or modified for the problem of triangular number division.
The trial definition of triangular number reciprocal TR(n) was derived. The original definition for triangular number was TN(n) = (n*(n+1)) / 2 ;# definition, n >= 1. Reciprocate both sides of equation as 1/TN(n) = 2 / (n*(n+1)). The trial definition for triangular number reciprocal is TR(n) = 2 / (n*(n+1)), n >= 1. In the TCL proc, the triangular number reciprocal is returned as floating point fp.
The Glaisher formula for Triangular Number product is aa * bb = TN <aa-1> + TN <bb> - TN <aa-bb-1>. For reciprocal multiplication, aa * bb * TR = <TN <aa-1> + TN <bb> - TN <aa-bb-1>> * TR. In a TCL proc, the result would be floating point fp.
- For reciprocal multiplication with Glaisher formula
- aa * bb = < TN <aa-1> + TN <bb> - TN <aa-bb-1>> ;# Glaisher formula for TN product
- multiply both sides by TR(), aa > bb
- aa * bb * TR() = < TN <aa-1> + TN <bb> - TN <aa-bb-1>> * TR()
- 7 * 3 * TR(2) = < TN <aa-1> + TN <bb> - TN <aa-bb-1>> * TR(2)
- 7 * 3 * 2/6 = < TN <6> + TN <3> - TN <3> > * 2/6
- 7 * 3 * 1/3 = < 21 + 6 - 6>> * 2/6
- 7 * 3 * 1/3 = 21 * 1/3
- 7 = 7
A triangular number multiplication formula was found that was thought a good model for triangular number division by reciprocal. The triangular multiplication formula was selected as m*n = TN(m+n) - TN(m) - TN(n) from the monograph, The Beauty of Triangular Numbers. The derivation was published from Mulatu Lemma, Savannah State university. As an aside, this triangular multiplication formula is exact for integer arithmetic and appears more robust and fool proof than the Glashier formula. There is less danger of a negative entry as TN(a-b-1) is not used here. And subbing for triangular number definitions, the formula would be the product m*n = (m+n)*(m+n+1)/2. -m*(m+1)/2. - n*(n+1)/2. Where m is a positive integer m>=1 and for reciprocal multiplication, positive reciprocal or eval 1./$r in floating point is loaded for n>=0. The formula was loaded in a TCL reciprocal proc as expr { ($m+$n)*($m+$n+1.)/2. -$m*($m+1.)/2. - $n*($n+1.)/2.}. The reciprocal proc with floating point entries appears to be off by one part in 10E6.
;# formula m*n = TN(m+n) - TN(m) - TN(n) ;# Theorem 2, Mulatu Lemma
;# subbing TN definitions into Theorem 2
;# multiplication formula m*n = (m+n)*(m+n+1)/2. -m*(m+1)/2. - n*(n+1)/2.
proc triangular_multiplication_tn { m n } {return [ expr { ($m+$n)*($m+$n+1)/2 - $m*($m+1)/2 - $n*($n+1)/2}] } ;# m >= 1, n>= 1
;# Usage triangular_multiplication_tn 10000000000000000000000000 2 -> 20000000000000000000000000
proc reciprocal_division_tn { m r } {set n [expr {1./ $r} ];return [ expr { ($m+$n)*($m+$n+1.)/2. -$m*($m+1.)/2. - $n*($n+1.)/2.}] }
;# m >= 1, r > = 1, {1./ $r} = $n, $n is reciprocal r in floating point
;# reciprocal proc appears to be off
;# by one part in 10E6.
;# Usage reciprocal_division_tn 4 .5 -> 2
;# Usage reciprocal_division_tn 999 .5 -> 499.5
;# Usage reciprocal_division_tn 1000000 .5 -> 500000.0
;# Usage reciprocal_division_tn 999999 .5 -> 499999.5
;# Usage reciprocal_division_tn 1000000000 .5
-> 499999999.625
;# Usage reciprocal_division_tn 1000000000000 .5
-> 499961036799.625
;# Usage reciprocal_division_tn 999999999999 .5 -> 499961036799.625- aa * bb = TN <aa-1> + TN <bb> - TN <aa-bb-1> ;# Glaisher formula for Triangular Number product
- T(m*n)= T(m)*T(n)+T(m-1)*T(n-1) ;# product law from David Radcliffe
- a*(a/b) = TN(a+(a/b)) + TN(a) - TN(a/b) ;# check Arnaudeau rewrite as a*(a/b) ,1869
- aa * (a/b) = TN <aa-1> + TN <(a/b)> - TN <aa-(a/b)-1> ;# rewrite Glaisher formula for aa * (a/b)
- Triangular Number Multiplication Formula
- derivation by Dr. Mulatu Lemma, Savannah State university
- TN(1)=1, TN(2)=3, TN(3)=6, TN(5)=15
- T(m+n) = T(m) + T(n) + m*n , Theorem 2 for positive integers
- m*n = T(m+n) - T(m) - T(n)
- 3*2 = T(3+2) - T(3) - T(2)
- 3*2 = T(5) - T(3) - T(2)
- 3*2 = 15 -6 -3 = 15 - 9
- 3*2 = 6
- 4 = 4 QED
- Triangular Number Reciprocal Formula
- TN(1)=1, TN(2)=3, TN(3)=6,
- 4*2 = TN(4-1) + TN(2) - TN(4-2-1)
- 4*2 = TN(3) + TN(2) - TN(1)
- 4*2 = 6 + 3 -1 = 8
- 4*(4/2) = TN(4-1) + TN(2) - TN(4-2-1) ;# multiply both side by 2
- 4*4 = TR(2) * < (TN(4-1) + TN(2) - TN(4-2-1)>
- Trial Definition of triangular number reciprocal TR(n)
- TN(n) = (n*(n+1)) / 2 ;# definition, n >= 1
- 1/TN(n) = 2 / (n*(n+1)) ;# reciprocate both sides of equation
- TR(n) = 2 / (n*(n+1)) ;# new legal? definition , n>= 1
;# speculative formula for reciprocals of triangular numbers
;# Sum reciprocal series to infinity 1/T(n) = 2 * ( 1 - 1/(n+1),
;# limit of reciprocal series is 2 at infinity
;# 1/(n+1) goes to zero at infinity
;# the difference of last two terms in series
;# would be T(n) - T(n-1), subbing (n-1) into nth term
;# TR = <2 * (1 - 1/ ( n + 1)> - <2 * (1 - 1/((n - 1) + 1)>
;# TR = 2 / (( n + 1 ) * n ) #; speculative formula
;# & extra spaces for clarity and bad eyes
proc reciprocal_tn {n} { return [expr { 2. / (( $n + 1 ) * $n ) } ] }
;# Usage reciprocal_tn 1 -> 1 ;# correct TN(1)=1, 1/TN(1) = 1
;# Usage reciprocal_tn 3 -> 0.166 ;# correct TN(3)=6, 1/TN(3) = 1/6
;# Usage reciprocal_tn 5 -> 0.066 ;# correct TN(5)=15, 1/TN(5) = 1/15
;# Usage reciprocal_tn 1000000 -> 1.99999E-12
;# correct TN(1000000)=500000500000.0, 1/TN(1000000) = 1/500000500000
;# Only thing is, my hokey math may conflict
;# with legal proofs of triangular numbers, n < 1 ???Conventional Identities with Triangular Numbers
Due to my bad eyes, normal subscripts are placed inside parentheses
- # constraints below on a and b , if any
- T(n)= 1 + 2 + 3 ... n = n * (n + 1 ) / 2. ;# explanation in similar notation
- choose (n+1 2) can be expressed as (n+1)!/ (n+1−2)!2!. Simplifies to n(n+1)/2
- T(0) = 0
- T(1) = 1
- T(n) = n * (n + 1 ) / 2
- T(n) + (n + 1 ) = T(n + 1 )
- T(n+1) = T(n) + (n + 1 ) ;# HOGGATT, JR., and MARJORIE BICKWELL
- n**2 = T(n) + T(n - 1) ;# HOGGATT, JR., and MARJORIE BICKWELL, also from Theon & Nicomachus
- n = T(a) + T(b) + T(c) ;# theorem for all n, n > 2
- 8 * T(n) + 1 = r**2 ;# theorem for all n, n > 2, from Plutarch
- 3 * T(n) + T(n-1) = T(2*n)
- T(n + 1 ) * T(n + 1 ) - T(n) * T(n) = (n+1)**3 ;# Joncourt uses this identity
- T(n) + (n+1) = T(n+1)
- (T(n-1))**2 - (T(n))**2 = (n+1)**3
- n*T(n+1) = (n+2)*T(n)
- square from Beauty of Triangular Numbers
- n**2 = n*(n-1)/2 + n(n+1)/2 ;# sub definitions
- n**2 = TN(n-1) + TN(n)
- 4**2 = TN(4-1) + TN(4)
- 16 = 6 + 10
- 16 = 16 QED
- deriving another TN formula for square
- test numbers: TN(1)=1, TN(2)=3, TN(3)=6, TN(4) =10 , TN(5)=15
- m*n = TN(m+n) - TN(m) - TN(n)
- m*m = TN(m+m) - TN(m) - TN(m) ;# sub m for n
- m*m = TN(m+m) - TN(m) - TN(m) ;# sub 5
- 5*5 = TN(5+5) - TN(5) - TN(5)
- 25 = 55 - 15 -15 = 55 - 30
- 25 = 25 QED
- TN(n-1):TN(n) ratio of terms in series approaches 1:1 at infinity
- TN(n)= n*(n+1)/2 = n**2/2 +n/2
- TN(n-1)= (n-1)*(n)/2 = n**2/2 - n/2
- TN(n-1):TN(n) = <n**2/2 - n/2> / <n**2/2 +n/2>
- = <n**2- n> / <n**2 +n>
- = <n- 1> / <n +1>
- = <1- 1/n> / <1 +1/n> , n -> infinity
- TN(n-1):TN(n) = 1:1 at infinity
Developing Square Root Identities and Cubes from Triangular Numbers
The formula for triangular number is m = n*(n+1)*.5 by definition. Standing back for some perspective, the triangular number definition gives the area of a right angle triangle with one side equal to n and one side equal to (n+1). Two of these triangles could form a rectangle with a short side as n and the long side as (n+1). The area of the rectangle is area2 = n*(n+1). For boundaries, n**2 =< area2 =< (n+1)**2. Also, it follows that n =< sqrt(area2) =< (n+1). The area2 may be considered the area of a square n**2 plus an additional layer and strip of one depth and n wide. The total area2 would be n**2 plus 1*n. One sees that the original definition of triangular number is partially a square, or like a figurate number sometimes called an oblong number or quasi square. A reverse triangular number might be effectively a square root function that deals with the extra strip of one depth and n wide.
- deriving another TN formula for square root
- trial for sqrt(n) = f(TN()), sqrt(n) in terms of TN’s
- test triangular numbers: TN(0)=0, TN(1)=1, TN(2)=3,
- TN(3)=6, TN(4) =10 , TN(5)=15, TN(6)=21, TN(6)=21, TN(7)=28, TN(9)=45,
- m*n = TN(m+n) - TN(m) - TN(n) ;# derivation was published from Mulatu Lemma, Beauty of Triangular Numbers
- m*m = TN(m+m) - TN(m) - TN(m) ;# sub m for n
- m*m = TN(m+m) - TN(m) - TN(m) ;# sub sqrt(n) for m
- sqrt(n) * sqrt(n) = TN(sqrt(n) + sqrt(n)) - TN( sqrt(n)) - TN( sqrt(n))
- sqrt(n) = < 1 / sqrt(n) > * < TN(sqrt(n) + sqrt(n)) - TN( sqrt(n)) - TN( sqrt(n))>
- following trials for case 0, case 1, case 4 : sqrt(4) = 2
- sqrt(0) = < 1 / (0) > * < TN(sqrt(0) + sqrt(0)) - TN( sqrt(0)) - TN( sqrt(0))> #; actual 1/(0) undefined
- sqrt(0) = 0? * < 0 - 0 - 0 >, sqrt(0) = 0?
- 0 = 0 QED
- sqrt(1) = < 1 / sqrt(1) > * < TN(sqrt(1) + sqrt(1)) - TN( sqrt(1)) - TN( sqrt(1))>
- sqrt(1) = < 1 > * < TN(2) - TN(1) - TN(1) > = < 1 > * < TN(2) - TN(1) - TN(1) >
- sqrt(1) = < 1 > * < 3 - 1 - 1 > = < 1 > * 1 = 1
- 1 = 1 QED
- sqrt(4) = < 1 / sqrt(4) > * < TN(sqrt(4) + sqrt(4)) - TN( sqrt(4)) - TN( sqrt(4))>
- sqrt(4) = < 1 / 2 > * < TN(2 + 2 ) - TN( 2 ) - TN( 2 ) >
- sqrt(4) = < 1 / 2 > * < TN(4 ) - TN( 2 ) - TN( 2 ) >
- sqrt(4) = < 1 / 2 > * < 10 - 3 - 3 > = < 1 / 2 > * < 4 >
- 2 = 2, QED
- sqrt(9) = < 1 / sqrt(9) > * < TN(sqrt(9) + sqrt(9)) - TN( sqrt(9)) - TN( sqrt(9))>
- sqrt(9) = < 1 / 3 > * < TN(3 + 3 ) - TN( 3 ) - TN( 3 ) >
- sqrt(9) = < 1 / 3 > * < TN(6 ) - TN( 3 ) - TN( 3 ) >
- sqrt(9) = < 1 / 3 > * < 21 - 6 - 6 > = < 1 / 3 > * < 9 >
- 3 = 3 , QED
gold 12/27/2020. Find square root of natural number 12.5, using inspection on Joncourt tables, using quadratic formula, and other interpolation methods. In this case, the entry number 12.5 is considered a square = n**2. Another complement square = (n+1)**2. Given from Joncourt table, TN(1)=1, TN(2)=3, TN(3)=6, TN(4)=10, TN(5)=15.
- 1) Using inspection on Joncourt tables.
- n**2 = TN(n) + TN(n+1) ;# Joncourt used this theorem
- TN(root) =~ .5 * ( n**2 ) ;# Joncourt used this theorem
- Find square root of 12.5 using triangular numbers
- expr {12.5 * .5 } = 6.25
- 6.25 is between triangular numbers 6 and 10
- inverse TN(6) <= sqrt( 12.5 ) <= inverse TN(10)
- 3 <= sqrt( 12.5 ) <= 4 ;# boundaries are natural numbers
- TN ratio expr { 6/10. }= 0.6
- 2) Using TCL procs for sqrt limits.
- sqrt_limits_joncourt 12.5 -> sqrt 12.5 from 3.0 to 4.0
- find ratio of triangular numbers 6 and 10
- expr {6./10. } -> 0.6
- 3 <= sqrt( 12.5 ) <= 4 ;# boundaries are natural numbers
- sqrt( 12.5*.5 ) = sqrt(6.25) = natural number 3 + square root fraction srtf (.25)
- root fraction srtf can be solved with the quadratic formula.
srtf 0.25 -> 0.5
- square root of 12.5 =~ 3 + 0.5 =~ 3.5
- check that expr {3.5**2} = 12.25, ~12.5
proc srtf {ttt} {return [ expr {((-2. + sqrt( 2.**2 -4.*1.*( 1. - $ttt )))/2.)+1.} ] }
# Usage srtf 0.25 -> 0.5- 3) The square root can be solved with triangular numbers using the quadratic formula.
- TN(root) =~ .5 * ( n**2 ) =~ inverse < .5 * < TN(n) + TN(n+1) > ;# Joncourt used this theorem
- sqrt_limits_joncourt 12.5 -> sqrt 12.5 from 3.0 to 4.0
- definition is triangular number m = n*(n+1)*.5
expr { 12.5 *.5 } = 6.25
- lower triangular limit = n*(n+1)*.5 = expr { 3*(3+1)*.5 } = 6.0
- upper triangular limit = n*(n+1)*.5 = expr { 4*(4+1)*.5 } = 10.0
- find ratio of triangular numbers 6 and 10
- expr {6./10. } -> 0.6
- square root = solve_sqrt 12.5 -> 3.5355339059327378
- TCL check is { 12.5**.5 } -> 3.5355339059327378
- TCL check is expr { 3.535**2 } -> 12.496 rounds to 12.5
Derive cube formula for TCL proc from Lemma Theorem 2. Clearly the Lemma Theorem 2 has opened a doorway for TCL into the theory of Triangular Numbers. Using TCL notation, almost any TCL evaluation of positive numbers can be subbed into Lemma Theorem 2 of Triangular Numbers. Sub n product with example TCL procs expr $k or [expr [k?]. Possibly sub o for floating point 1.
- derive cube formula from Lemma Theorem 2
- T(m+n) = T(m) + T(n) + m*n ;# Lemma Theorem 2
- T(m+n) = T(m) + T(n) + m*n ;# sub m with m*o
- T(m*o+n) = T(m*o) + T(n) + m*o*n
- m*o*n = T(m*o+n) -T(m*o) - T(n) ;# sub m&o with n
- n*n*n = T(n*n+n) -T(n*n) - T(n)
- ;# sub n product with example TCL procs expr $k or
expr [k? ],
- possibly sub o for floating point 1.
- sub Theorem 2, expr k?*o*n = T(expr k?*o+n) -T(expr k?*o) - T(n)
proc cube_tn3 {n} {return [+ [trinity [+ [* $n $n] $n ]] [* -1. [trinity [* $n $n] ]] [* -1. [trinity $n]] ]}
;# Usage cube_tn3 2 -> 8 ;# Usage cube_tn3 3 -> 27
;# Usage cube_tn3 1000 -> 1000000000.0
;# Usage cube_tn3 1000.999999 -> 1003002997.9940435Gifts from the Song “ Twelve Days of Christmas
Find the daily number of gifts and grand total of gifts from the song “ Twelve Days of Christmas” using Triangular Numbers, and guest staring Tetrahedral Numbers TETN and Triangular Pyramids. Each subtotal for a day’s gifts is a Triangular Number TN. The gifts from Total_Twelve_Days is expr { TN(1)+TN(2)+TN(3)+TN(4)+TN(5)+TN(6)+TN(7)+TN(8)+TN(9)+TN(10) +TN(11) +TN(12) }. The TCL expression is expr {1 + 3 + 6 + 10 + 15 + 21+ 28 + 36 + 45 + 55 + 66 + 78 } = 364 gifts. The quick answer is that the Tetrahedral Number TETN has the formula (n+(n+1)+(n+2))/6. TETN(12) = expr {($n*($n+1)*($n+2))/6. } = expr {(12*(12+1)*(12+2))/6. } = 364 gifts. What about a year of gifts? TETN(364) = expr {($n*($n+1)*($n+2))/6. } = expr {(364*(364+1)*(364+2))/6. } = 8104460 gifts. Rearranging terms, the definition for Triangular Number TN can be found hidden inside the Tetrahedral formula ($n*($n+1)/2) * (($n+2))/3.). The Tetrahedral formula as expr {($n*($n+1)*($n+2))/6. } can be proportional and related to the volume of a triangular pyramid using the $n expressions as linear dimensions. Credit Brent Yorgey, mathlesstraveled website
proc tetrahedral_TETN { n } { return [expr {($n*($n+1)*($n+2))/6. } ]}Analogs to Volume of Boxes and Triangular Pyramids
A clay tablet for solving cubic equations has found, probably from ancient city of Larsa, Sumer, Modern Iraq, BCE 2000. For the left entry values 1 to 30, the right value on the clay tablet equals { n*(n+1)*(n+2) }. The modern Tetrahedral formula in TCL notation as expr {($n*($n+1)*($n+2))/6. } can be proportional and related to the volume of a triangular pyramid using the $n expressions as linear dimensions. Treat the $n expressions as linear dimensions < width = $n> *< length = ($n+1)>* < height = ($n+2) >. The assignment of $n, ($n+1), and ($n+2) to respective width and length is arbitrary, but does seem to track with a limited set of problems. A box or cellar would have a volume of <width= $n> *< length = ($n+1)> * < height = ($n+2) >. The volume of a triangular pyramid is (1/3) * ( base_area ) * height. Subbing a right triangle as base for the triangular pyramid, the volume is (1/3) * ( 1/2 ) * width * length * height. The volume of this triangular pyramid with a triangular base is (1/3) * ( 1/2 ) *<width= $n> *< length = ($n+1)> * < height = ($n+2) >. The volume of the cellar is equivalent to the same volume of 6 triangular pyramids with triangular bases of the given dimensions. On the clay tablet n is the root and the tablet is used to find the inverse triangular number.
The volume of a triangular pyramid is (1/3) * ( base_area ) * height. Subbing a square or rectangle as base for the triangular pyramid, the volume is (1/3) * width * length* height. Continuing in a similar manner, the volume of this triangular pyramid with a rectangular base is (1/3) *<width= $n> *< length = ($n+1)> * < height = ($n+2) >. The volume of the cellar is equivalent to the same volume of 3 triangular pyramids with rectangular bases of the given dimensions.
Cannonballs stacked into Pyramids
Find the number of cannonballs in a triangular pyramid with a triangular base TP_TB using Triangular Numbers. The definition is TN = <(n)*(n+1)/2 >. The formula for cannonballs in a triangular pyramid is TP_TB = (n/6)*(n+1)*(n+2). If the TP_TB formula is transformed, one can see the Triangular Number definition hidden inside. TP_TB = <(n)*(n+1)/2 > * <(n+2)/3>. Subbing the definition, TP_TB = TN(n)* <(n+2)/3> . The infinite series is 'TP_TB(n) = {1, 4, 10, 20, 35, 56, 84, 120, …} from OEIS A000292, Tetrahedral or triangular pyramidal numbers. Using Triangular Numbers, one triangular pyramid with a triangular base TP_TB with a layer of one has one cannonball. A TP_TB with two layers has 4 cannonballs; a TP_TB with three layers has 10 cannonballs; a TP_TB with four layers has 20 cannonballs, and so on to infinity.
Find the number of cannonballs in a triangular pyramid with a square base TP_SB using Triangular Numbers. The definition is TN = <(n)*(n+1)/2 >. The formula for cannonballs in a triangular pyramid with a square base is TP_SB = (n/6)*(n+1)*(2*n+1). If the TP_SB formula is transformed, one can see the Triangular Number definition hidden inside. TP_SB = <(n)*(n+1)/2 > * <(2*n+2)/3>. Subbing the definition, TP_SB = TN(n) * <(2*n+1)/3> . The infinite series is TP_SB(n) = { 1, 5, 14, 30, 55, 91, 140, 204,.} from OEIS A000330, Square pyramidal numbers. Using Triangular Numbers, one triangular pyramid with a square base TP_SB with a layer of one has one cannonball. A TP_SB with two layers has 5 cannonballs; a TP_SB with three layers has 14 cannonballs; a TP_SB with four layers has 30 cannonballs, and so on to infinity.
;# triangular pyramid with triangular base
proc pyramid1 { n } {return [ expr { $n*($n+1)*($n+2)*(1./6)}] }
;# Usage pyramid1 0 -> 0.0 ;# pyramid1 1 -> 1.0
;# Usage pyramid1 4 -> 20.0
;# Usage pyramid1 100 -> 171700.0
;# triangular pyramid with square base TP_SB
;# formula n*(n+1)*(2*n+1)/6.
proc pyramid2 { n } {return [ expr { $n*($n+1)*(2*$n+1)*(1./6)}] }
;# Usage pyramid2 0 -> 0.0 ;# pyramid2 1 -> 1.0
;# Usage pyramid2 5 -> 55.0
;# Usage pyramid2 1000000 -> 3.333E+17
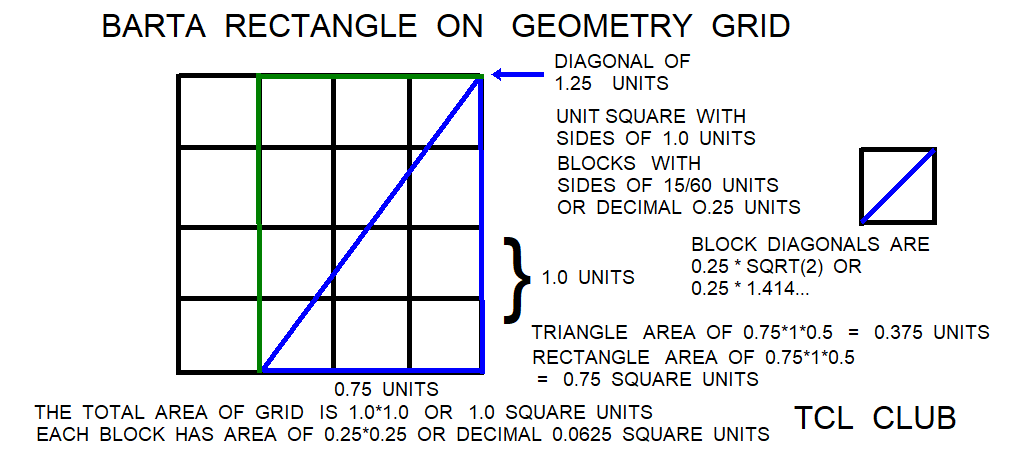
BarTa Rectangle in the Babylonian math problems <draft>
One of the favorite rectangles in the Babylonian math problems was the Bar-Ta rectangle. The linguists are saying that Bar-ta or Dar-Ta means cross bar, cross piece, or transversal in the tablet glyphs, see Muroi. The Bar-Ta rectangle is related to the 3/4/5 triangle scaled by 1/4. Meaning divide the dimensions of the 3/4/5 triangle by 4 to get 3/4 4/4 5/4>. The Bar-Ta rectangle is two of the rescaled triangles. The conceptual math problem asks for the sides of a rectangle whose area is 0:45 and whose diagonal is 1;15 in base_60. Converting to base_10, the equivalent decimal numbers are 0.75 for the area, and 1.25 for the diagonal. Then in decimal, Side a = 1 , then side b= 0.75. area a*b = 0.75 decimal.
The Barta triangle was used in terms of a comparison using the conventional modern trigonometry of sin/tangent and the concepts of Rational Trigonometry, reference to expanded P322(CR-Decimal8) table in Mansfield and Wildberger on P322 table. The first part is to identify the triangle or closest Babylonian triplet on P322. The beta or b/l equals (3/4)/1 as expr { (3/4.)/1.} or 0.75 units. The delta or d/l equals (1.25)/1 as expr { (1.25)/1.} or 1.25 units. The delta squared or (d/l)**2 equals ((1.25)/1)**2 as expr { ((1.25)/1.)**2} or 1.5625 decimal units. The equivalent line on P322 was line 11 and the triplet in base_60 was ( 45/60, 1, 1+15/60 ). Most of the linguists agree that the lines on the tablet are triangles normalized to a length l of unity. The normalized triangles are reduced mostly to sides with no common factors other than 1, hence the high proportions of prime numbers on the tablet. For comparison in modern angles, the angle A was arctangent expr { .75/1 } or 36.869 degrees. The angle B was arctangent expr { .75/1 } or 53.129 degrees. The diagonal equals expr {((1.*1)+(.75*.75))**.5 } or 1.25 decimal.
Unless the problem uses one of the special triangles, it is believed that the triangle would have to be normalized and rescaled to a middle side of 1, solved with the Babylonian triplets, then the answers rescaled and interpolated to the orignal size.
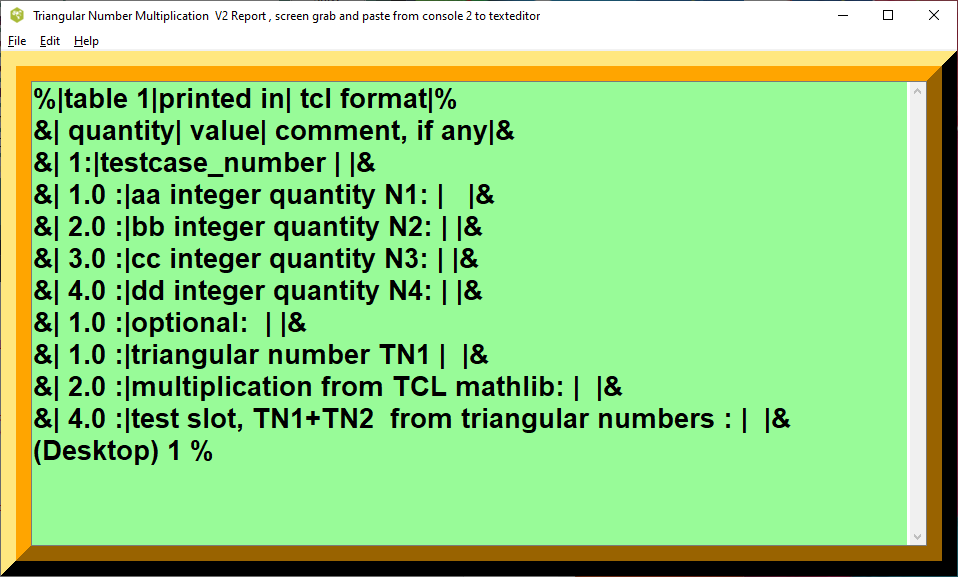
Push Button Operation
For the push buttons, the recommended procedure is push a testcase and fill frame, change first three entries etc, push solve, and then push report. Report allows copy and paste from console. For testcases in a computer session, the TCL calculator increments a new testcase number internally, eg. TC(1), TC(2)., TC(3), TC(4) etc. The testcase number is internal to the calculator and will not be printed until the report button is pushed for the current result numbers. The current result numbers will be cleared on the next solve button. For comparison of the Babylonian algorithm with conventional Western methods, TCL code will include redundant procs, redundant calculation paths, and printout check formulas to compute product and area.
Conclusions
The Old Babylonian quarter squares multiplication formula requires three math operations as opposed to one math operation in modern logarithms, per two numbers. Considering hand calculations and omitting the table lookups, the Old Babylonian quarter squares multiplication formula is about three times the work of the modern logarithm method. Under the same considerations, the Old Babylonian half squares multiplication formula requires four math operations and is about four times the work of the the modern logarithm method. In using the Babylonian multiplication formula in taking base_60 squares, using many place numbers in a hand multiplication array, there must be breakpoints where the effort of the multiplication formula is less than taking the many place square by hand calculation. Given the amount of Babylonian effort that developed the many place reciprocals in base_60 on the clay tablets, is it possible that the known Babylonian multiplication formulas, base_60 reciprocals, and terms could be manipulated into an algorithm, formula, or even modern logarithm of fewer operations?
Both the Triangular Number TN multiplication formulas used here require 3 table look ups and at least two math operations, referring to manual calculation. There was no particular time saving in Triangular Number TN multiplication over the Quarter Squares method in manual calculation. However, believe that the Triangular Number TN multiplication and other TN formulas are more flexible and easier to implement in TCL computer code.
The triangular numbers have the amazing property of multiplication in formulas using addition and and subtraction of Triangular Numbers TN. The published formulas have been adapted for the creation of multiplication products, squares, cubes, finding square roots, and division by reciprocal multiplication. Clearly the Lemma Theorem 2 has opened a doorway for TCL into the theory of Triangular Numbers. Using TCL notation, almost any TCL evaluation of positive numbers can be subbed into the Lemma Theorem 2 of Triangular Numbers.
Table 1 : Triangular Numbers Study
| Table 1: Triangular Numbers Tables | printed in | tcl format |
|---|---|---|
| a | subbing a*(a+1)*.5 number series | comments if any |
| 0 | 0.00000 | |
| 1 | 1.0000 | |
| 2 | 3.0000 | |
| 3 | 6.0000 | |
| 4 | 10.000 | |
| 5 | 15.000 | |
| 6 | 21.000 | |
| 7 | 28.000 | |
| 8 | 36.000 | |
| 9 | 45.000 | |
| 10 | 55.000 | |
| 11 | 66.000 | |
| 12 | 78.000 | |
| 13 | 91.000 | |
| 14 | 105.00 | |
| 15 | 120.00 | |
| 16 | 136.00 | |
| 17 | 153.00 | |
| 18 | 171.00 | |
| 19 | 190.00 | |
| 20 | 210.00 |
Table 2 : Proof of Abu Al Karachi
formula 1**3 + 2**3 + 3**3 ... + N**3 = ( 1 + 2 + 3 ... + n)**2
| table 2 | printed in | TCL format | |
|---|---|---|---|
| expression | answer | comment, if any | |
| expr { 1 } | ;# -> 1 | ||
| expr { 1 + 2 } | ;# -> 3 | ||
| expr { 1 + 2 + 3 } | ;# -> 6 | ||
| expr { 1 + 2 + 3 + 4 } | ;# -> 10 | ||
| expr { 1 + 2 + 3 + 4 + 5 } | ;# -> 15 | ||
| expr { 1**3 } | ;# -> 1 | ||
| expr { 1**3 + 2**3 + } | ;# -> 9 | ||
| expr { 1**3 + 2**3 + 3**3 } | ;# -> 36 | ||
| expr { 1**3 + 2**3 + 3**3 + 4**3} | ;# -> 100 | ||
| expr { 1**3 + 2**3 + 3**3 + 4**3 + 5**3 } | ;# -> 225 |
Table 3 : Powers of 2 with added Modern Logarithm Notation
| Table 3: Powers of 2 | printed in | tcl format | ||
|---|---|---|---|---|
| N | 2**N | modern notation log2 N = | base_60 reciprocal, decimals | comments if any |
| 0 | 1.0000 | log2 1 = 0.0 | 60.000 | |
| 1 | 2.0000 | log2 2 = 1.0 | 30.000 | |
| 2 | 4.0000 | log2 4 = 2.0 | 15.000 | Ref MCT |
| 3 | 8.0000 | log2 8 = 3.0 | 7.5000 | |
| 4 | 16.000 | log2 16 = 4.0 | 3.7500 | |
| 5 | 32.000 | log2 32 = 5.0 | 1.8750 | |
| 6 | 64.000 | log2 64 = 6.0 | 0.93800 | |
| 7 | 128.00 | log2 128 = 7.0 | 0.46900 | |
| 8 | 256.00 | log2 256 = 8.0 | 0.23400 | |
| 9 | 512.00 | log2 512 = 9.0 | 0.11700 | |
| 10 | 1024.0 | log2 1024 = 10.0 | 0.059000 |
Table 4 : Standard Multiplication Table
| Multiplication Table | printed in | tcl format | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 | 22 | 24 | |
| 3 | 9 | 12 | 15 | 18 | 21 | 24 | 27 | 30 | 33 | 36 | ||
| 4 | 16 | 20 | 24 | 28 | 32 | 36 | 40 | 44 | 48 | |||
| 5 | 25 | 30 | 35 | 40 | 45 | 50 | 55 | 60 | ||||
| 6 | 36 | 42 | 48 | 54 | 60 | 66 | 72 | |||||
| 7 | 49 | 56 | 63 | 70 | 77 | 84 | ||||||
| 8 | 64 | 72 | 80 | 88 | 96 | |||||||
| 9 | 81 | 90 | 99 | 108 | ||||||||
| 10 | 100 | 110 | 120 | |||||||||
| 11 | 121 | 132 | ||||||||||
| 12 | 144 |
Reference. Gnumeric Spreadsheet.
Table 5 : Standard Multiplication Table, another
| Multiplication Table | printed in | tcl format | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | X |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
| 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 | 22 | 24 | |
| 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 | 27 | 30 | 33 | 36 | |
| 4 | 8 | 12 | 16 | 20 | 24 | 28 | 32 | 36 | 40 | 44 | 48 | |
| 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 | 55 | 60 | |
| 6 | 12 | 18 | 24 | 30 | 36 | 42 | 48 | 54 | 60 | 66 | 72 | |
| 7 | 14 | 21 | 28 | 35 | 42 | 49 | 56 | 63 | 70 | 77 | 84 | |
| 8 | 16 | 24 | 32 | 40 | 48 | 56 | 64 | 72 | 80 | 88 | 96 | |
| 9 | 18 | 27 | 36 | 45 | 54 | 63 | 72 | 81 | 90 | 99 | 108 | |
| 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 | 110 | 120 | |
| 11 | 22 | 33 | 44 | 55 | 66 | 77 | 88 | 99 | 110 | 121 | 132 | |
| 12 | 24 | 36 | 48 | 60 | 72 | 84 | 96 | 108 | 120 | 132 | 144 |
Reference. Gnumeric Spreadsheet.
Table 6 : Figurate Formulas and TCL Procs Table
| Table Figurate Formulas and TCL Procs | printed in | tcl format | ||
|---|---|---|---|---|
| figurate name | formula in variable n | automatic trial TCL proc ************************ | infinite series | comment, if any |
| oblong numbers | n*(n+1) | proc figurate1 { n } {return [ expr {($n+1) }} | 0, 2, 6, 12, 20, 30, 42, 56, 72, 90, 110, ... | |
| triangular numbers | n*(n+1)/2 | proc figurate1 { n } {return [ expr {($n+1)/2}} | 1 3 6 10 15 21 28... | |
| square numbers | n**2 | proc figurate1 { n } {return [ expr {$n**2}} | 1 4 9 16 25 36 49... | |
| pentagonal numbers | n*(3n-1)/2 | proc figurate1 { n } {return [ expr {(3*$n-1)/2}} | 1 5 12 22 35 51 70... | |
| hexagonal numbers | n*(4n-2)/2 | proc figurate1 { n } {return [ expr {(4*$n-2)/2}} | 1 6 15 28 45 66 91... | |
| heptagonal numbers | n*(5n-3)/2 | proc figurate1 { n } {return [ expr {(5*$n-3)/2}} | 1 7 18 34 55 81 112... | |
| octogonal numbers | n*(3n-2) | proc figurate1 { n } {return [ expr {(3*$n-2)}} | 1 8 21 40 65 96 133... | |
| ********************** | 2D figurate numbers into 3D figurate numbers | ************************ | ||
| triangular numbers | n*(n+1)/2 | proc figurate1 { n } {return [ expr {($n+1)/2}} | 1 3 6 10 15 21... | |
| tetrahedral numbers | n*(n+1)*(n+2)/6 | proc figurate1 { n } {return [ expr {($n+1)*($n+2)/6}} | 1 4 10 20 35 56... | |
| hypertetrahedral numbers | n*(n+1)*(n+2)*(n+3)/24 | proc figurate1 { n } {return [ expr {($n+1)*($n+2)*($n+3)/24}} | 1 5 15 35 70 126... |
from Gnumeric spreadsheet
proc figurate1_oblong { n } {[ return [ expr {($n+1) }]}
proc figurate2_triangular { n } {[ return [ expr {($n+1)/2}]}
proc figurate3_square { n } {[ return [ expr {$n**2}]}
proc figurate4_pentagonal { n } {[ return [ expr {(3*$n-1)/2}]}
proc figurate5_hexagonal { n } {[ return [ expr {(4*$n-2)/2}]}
proc figurate6_heptagonal { n } {[ return [ expr {(5*$n-3)/2}]}
proc figurate7_octogonal { n } {[ return [ expr {(3*$n-2)}]}
;# ***** 2D figurate into 3D figurate $numbers ******
proc figurate8_triangular { n } {[ return [ expr {($n+1)/2}]} ;# duplicate proc for comparison
proc figurate9_tetrahedral { n } {[ return [ expr {($n+1)*($n+2)/6}]}
proc figurate10_hypertetrahedral { n } {[ return [ expr {($n+1)*($n+2)*($n+3)/24}]}Testcases Section
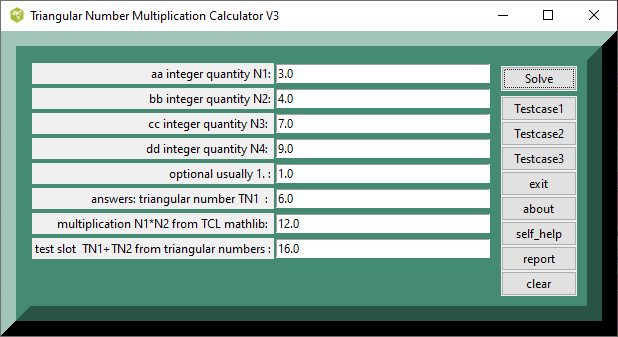
Testcase 1
| table 1 | printed in | tcl format |
|---|---|---|
| quantity | value | comment, if any |
| 1: | testcase_number | |
| 1.0 : | aa integer quantity N1: | |
| 2.0 : | bb integer quantity N2: | |
| 3.0 : | cc integer quantity N3: | |
| 4.0 : | dd integer quantity N4: | |
| 1.0 : | optional: | |
| 1.0 : | triangular number TN1 | |
| 2.0 : | multiplication from TCL mathlib: | |
| 4.0 : | test slot, TN1+TN2 from triangular numbers : |
Testcase 2
| table 2 | printed in | tcl format |
|---|---|---|
| quantity | value | comment, if any |
| 2: | testcase_number | |
| 3.0 : | aa integer quantity N1: | |
| 4.0 : | bb integer quantity N2: | |
| 7.0 : | cc integer quantity N3: | |
| 9.0 : | dd integer quantity N4: | |
| 1.0 : | optional: | |
| 6.0 : | triangular number TN1 | |
| 12.0 : | multiplication from TCL mathlib: | |
| 16.0 : | test slot, TN1+TN2 from triangular numbers : |
Testcase 3
| table 3 | printed in | tcl format |
|---|---|---|
| quantity | value | comment, if any |
| 3: | testcase_number | |
| 3.0 : | aa integer quantity N1: | |
| 6.0 : | bb integer quantity N2: | |
| 5.0 : | cc integer quantity N3: | |
| 7.0 : | dd integer quantity N4: | |
| 1.0 : | optional: | |
| 6.0 : | triangular number TN1 | |
| 18.0 : | multiplication from TCL mathlib: | |
| 27.0 : | test slot, TN1+TN2 from triangular numbers : |
Testcase 4 testing block procedure
| table 3 | printed in | tcl format |
|---|---|---|
| quantity | value | comment, if any |
| 4: | testcase_number | |
| 777.0 : | aa integer quantity N1: | |
| 778.0 : | bb integer quantity N2: | |
| 3.0 : | cc integer quantity N3: | |
| 4.0 : | dd integer quantity N4: | |
| 302253.0 303031.0 6.0 10.0 : | optional: | |
| 302253.0 : | triangular number TN1 | |
| 604506.0 : | multiplication from TCL mathlib: | |
| 604506.0 : | test slot >> multiplication TN1*TN2 from triangular numbers : | |
| >>>>> | testing block procedure | <<<< |
| 15.0 3.0 6.0 10.0 | test slot >> TN1*TN2 : | |
| TN <1 2 3 4 > returns 3.0 6.0 10.0 | test slot >> TN1 TN2 : | |
| TN <1 2 0 4 > returns 3.0 10.0 | test slot >> TN1 TN2 : | |
| TN <1 2 0 0 > returns 3.0 | test slot >> TN1 TN2 : | |
| TN <1 2 -3 4 > returns 3.0 -6.0 10.0 | test slot >> TN1 TN2 : | |
| TN < .1 .2 .3 .4 > returns 0 0 0 0 | test slot >> TN1 TN2 : | |
| TN < .1 .2 0. .4 > returns 0 0 0 | test slot >> TN1 TN2 : | |
| TN < 0. > returns 0 | test slot >> TN1 TN2 : | |
| TN < 1. > returns 0 | test slot >> TN1 TN2 : | |
| TN <10 20 30 40> returns 55.0 210.0 465.0 820.0 | test slot >> TN1 TN2 : | |
| >>>> | test invoking TCLLIB library | <<<< |
| = 0.33333333333333331 huge = 1.7976931348623157e+308 | ||
| math choose statements 45 6 55 | ||
| >>>> | testing large number | <<<< |
| 302253.0 303031.0 6.0 10.0 301476.0 303031.0 -1.0 604506.0 | ||
| 604506.0 777.0 778.0 604506.0 | ||
| Check TN<777> + TN<778> should equal square. | ||
| expr { 302253.0 + 303031.0} #= 605284.0 | ||
| expr { 605284.0**.5 } #= 778.0 clean root | ||
| Check sum of Glaisher terms should equal product. | ||
| expr { 301476.0 + 303031.0 -1.0 } #= 604506.0 | ||
| expr { 777*778 } #= 604506 from mathlibc |
Screenshots Section
figure 1. Calculator Screenshot
figure 1b. Calculator Screenshot
figure 2.Triangular Number chart
figure 3. Favorite
figure 4. Triangular Numbers in box
figure 5a. Sum successive TN(S) and get square.
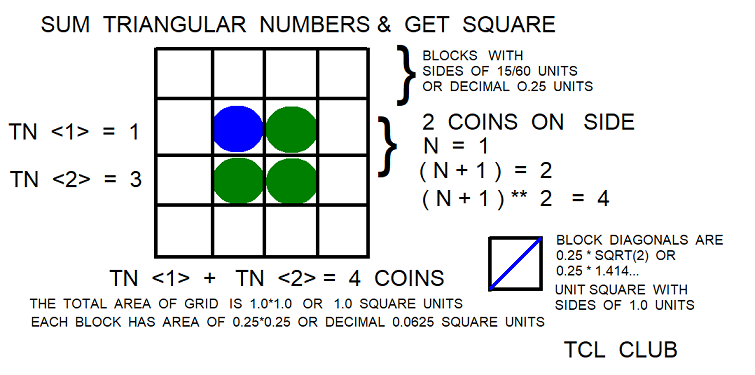
figure 5a'. Checker Board Random Colors
Note. Happenstance 3 + 1 squares on checker board of 3 random colors. These are 7 random 3+1 patterns on 3 color checker board.
figure 5b. Sum successive TN(S) and get square of 4 coins.
figure 5c. Sum successive TN(S) and get square
figure 5d. Sum successive TN(S) on small checker board
figure 5e. Sum successive TN(S) on checker board n**2=36
[L1 ]
figure 5f. Sum successive TN(S) on checker board
figure 6. Euclid Multiplication proof?
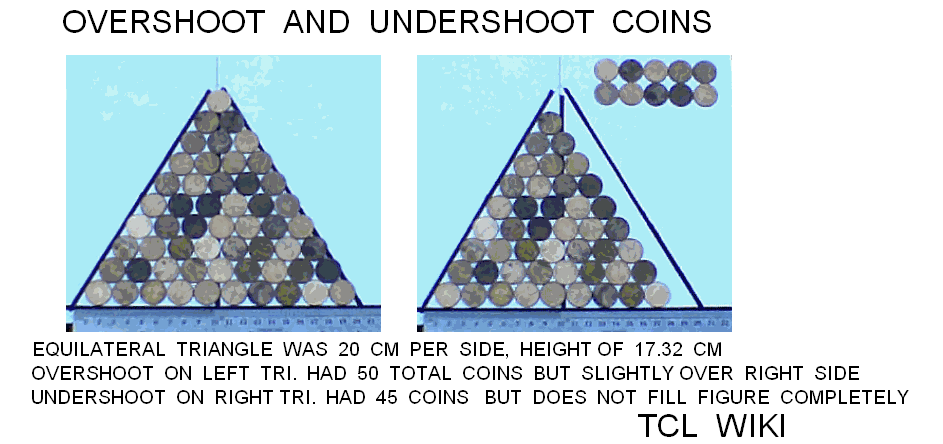
figure 7.Overshoot and Undershoot Coins
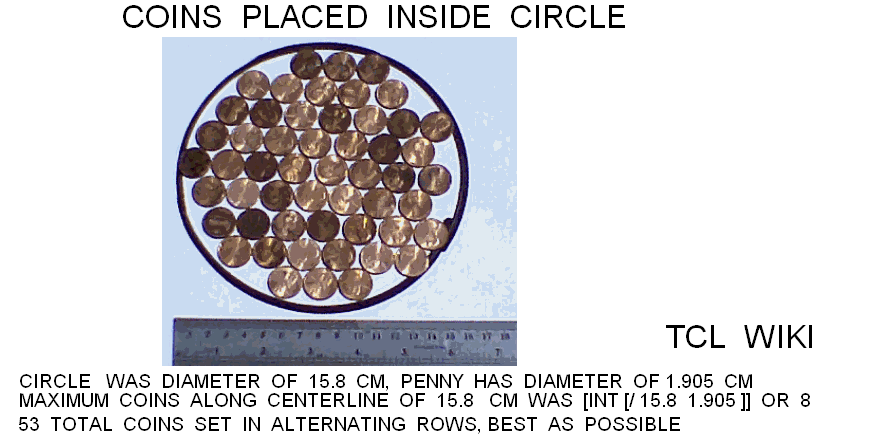
figure 8.Coins Placed inside Circle
figure 9.Second Try for Coins inside Circle
figure 10. Pascal's Triangle
Photo Attribution. By No machine-readable author provided. Drandstrom assumed (based on copyright claims). Own work assumed (based on copyright claims)., Public Domain, https://commons.wikimedia.org/w/index.php?curid=1674498
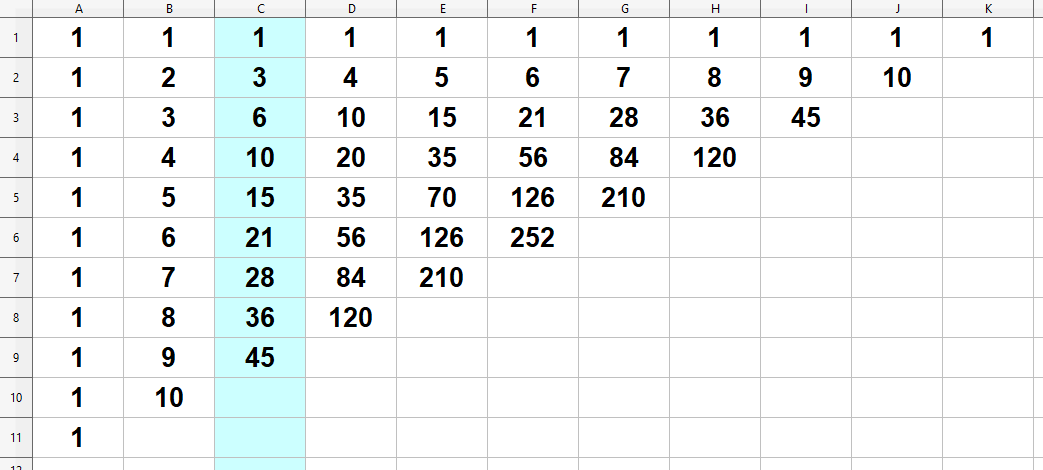
figure 11. Pascal's Triangle Spreadsheet
- triangular numbers in blue pastel
- column to left of blue pastel is natural numbers
- column to right of blue pastel is sum of triangular numbers
- column to right is Tetrahedral or triangular pyramidal numbers: 0, 1, 4, 10, 20, 35, 56, 84,
- triangular numbers in blue pastel
- column to left of blue pastel is natural numbers
- column to right of blue pastel is sum of triangular numbers
- column to right is Tetrahedral or triangular pyramidal numbers: 0, 1, 4, 10, 20, 35, 56, 84,
figure 12. Nicomachus Music Triangle Spreadsheet
- MUSIC TRIANGLE FROM NICOMACHUS TCL CLUB
- FIRST ROW IS POWERS OF 2
- LEFT SIDE IS POWERS OF 3
- TRIANGLE CONTAINS ALL NUMBERS CONSISTING OF < 2**M X 3**N >
figure 13. Stacking Cannonballs use Triangular Numbers
Fort Zachary Taylor, Florida, Photo Credit by Meriç Dağlı on Unsplash
References:
- Primary references, Google <Babylonian Multiplication by M. Lewinter and W. Widulski>
- Amazing-Traces-of-a-Babylonian-Origin-in-Greek-Mathematics,
- Joran Friberg. Primary reference
- google < Babylonian trapezoid Wikipedia >
- Wikipedia search engine < quarter square multiplication algorithm >
- Wikipedia search engine < multiplication algorithm > Primary reference
- Wikipedia search engine < Babylonian Math >
- Wikipedia search engine < history of logarithms >
- Wikipedia search engine < Special right triangle >
- precision math procedure used in TCL calculator Arjen Markus AM
- Computers and real numbers
- Floating-point formatting
- On Multiplication by a Table of Single Entry.
- J.W.L. Glaisher M.A. F.R.S., F.R.S.(1878)
- Denis Roegel. A reconstruction of Plassmann’s table of quarter-squares (1933).
- <Research Report> 2013, hal-00880838
- Denis Roegel. A reconstruction of Blater’s table of quarter-squares (1887).
- <Research Report> 2013, hal-00880836
- Denis Roegel. A reconstruction of Laundy’s table of quarter-squares (1856).
- <Research Report> 2013, hal-00880835
- Denis Roegel. A reconstruction of Joncourt's table of triangular numbers (1762)
- De natura et praeclaro usu simplicissimae
- speciei numerorum trigonalium, Autor, Joncourt, Élie
- Ancient Babylonian Algorithms, Donald E. Knuth, Stanford
- Mixed sums of squares and triangular numbers (III)
- Byeong-Kweon Oh a,1, Zhi-Wei Sun
- Department of Applied Mathematics, Sejong University
- Series of Reciprocal Triangular Numbers
- Paul Bruckman, Joseph B. Dence, Thomas P. Dence,
- and Justin Young
- On the representation of integers as sums of triangular numbers
- KEN ONO, SINAI ROBINS, AND PATRICK T. WAHL
- A reconstruction of Arnaudeau’s table of triangular numbers (ca. 1896)
- Denis Roegel
- On Triangular Numbers Which are Sums of Consecutive Squares
- RAPHAEL FINKEJSTEIN, Department of Mathematics, Bowling Green State University,
- hal-00654428v1 Reports
- Denis Roegel. A reconstruction of Gingerich's table of
- regular sexagesimals and a cuneiform version of the table (1965)
- Denis Roegel. A reconstruction of Arnaudeau’s table of triangular numbers (ca. 1896)
- Research Report LORIA - Université de Lorraine. 2014
- Denis Roegel. A reconstruction of Centnerschwer's table of quarter-squares (1825)
- Research Report, 2013
- Denis Roegel. A reconstruction of Merpaut's table of quarter-squares (1832)
- Research Report, 2013
- Denis Roegel. A reconstruction of Laundy's table of quarter-squares (1856)
- Research Report] 2013
- Denis Roegel. A reconstruction of Plassmann's table of quarter-squares (1933)
- Research Report, 2013
- Denis Roegel. A reconstruction of Blater's table of quarter-squares (1887)
- 2013
- Denis Roegel. A reconstruction of Bojko's table of quarter-squares (1909)
- 2013
- Denis Roegel. A reconstruction of Bürger's table of quarter-squares (1817)
- The Fascinating Mathematical Beauty of Triangular Numbers
- Especially see Theorem 2 on Triangular Multiplication.
- Digital Commons @ the Georgia Academy of Science.
- by Stacy Cobb, Natasha Patterson, Mulatu Lemma, Savannah State university
- Savannah, GA 3140
- Squares, triangles and other labour-saving devices, Burkard Polster and Marty Ross
- The Age, 17 March 2014, [L2 ]
- Multiplication formulas [L3 ]
- en.wikipedia.org, James_Whitbread_Lee_Glaisher
- mathforum.org/library/drmath/ Doctor Mitteldorf at MathForum
- en.wikipedia.org search engine on Multiplication_algorithm
- en.wikipedia.org search engine on Quarter square multiplication
- Triangular_numbers [L4 ]
- Figurate_numbers [L5 ]
- Orthoplex_numbers [L6 ]
- al-Karaji, Al Karachi [L7 ]
- al-Karaji, Al Karachi [L8 ]
- Dicuil (9th century) on Triangular and Square Numbers
- Helen Elizabeth Ross, British Journal for the History of Mathematics 2019, 34(2), 79-94
- Quotes from Method of Quarter Squares, James Glaisher,1889 & reprinted several times
- The American Philosophical Society Journal at Philadelphia
- Glaisher, J. The Method of Quarter Squares. Nature 41, 9 (1889).
- Journal of the Institute of Actuaries, Volume 28; Volume 28
- Glaisher, J. W. L., and G. CAREY FOSTER. “The Method of Quarter Squares.”
- Journal of the Institute of Actuaries (1886-1994), vol. 28, no. 3, 1890, pp. 227–235.
- Thomas Harriot's Doctrine of Triangular Numbers_ the `Magisteria Magna', England, 1618
- The Fascinating Mathematical Beauty of Triangular Numbers,
- Georgia Journal of Science, Vol. 66, No. 2, Article 9.2008
- The Mathematical Magic of Perfect Numbers," Georgia Journal of Science,
- Vol. 66, No. 2, Article 4.2008
- Elstak, Iwan R. and Goel, Sudhir (2014) "Find Square and Higher Order Roots,"
- Georgia Journal of Science, Vol. 72, No. 2, Article 3.
- Note On the Two Celebrity Numbers, Perfect Numbers and Triangular Numbers,
- M Lemma, R Quillet - EPH-International Journal of Mathematics and …, 2019
- Credit Brent Yorgey on Christmas series, mathlesstraveled website
- original quote in English for the Glaisher formula
- a * b = (1/2) * (a -r) * a + (1/2) * b * (b + r) - n * (a - b -r) * (a - b) ;# Glaisher general formula, variant
- or, as we may write it,
- a * b = T(a -1) + T(b) - T(a -1 -b) # Glaisher formula for multiplication
original quote in English " T (n) denotes the nth triangular number. Thus, to multiply two numbers we subtract unity from the larger number, and enter the table with the larger number so diminished, with the smaller number, and with the difference of these two numbers."-Glaisher
| Published Tables of Western Quarter-Squares | |||
|---|---|---|---|
| Table | Range | Pages | Density |
| Voisin (1817) | 20000 | 123 | 162.6 |
| Bürger (1817) | 20000 | 80 | 250.0 |
| Centnerschwer (1825) | 20000 | 40 | 500.0 |
| Merpaut (1832) | 40000 | 400 | 100.0 |
| Kulik (1851) | 30000 | 40 | 750.0 |
| Laundy (1856) | 100000 | 200 | 500.0 |
| Blater (1887) | 200000 | 200 | 1000.0 |
| Bojko (1909) | 20000 | 20 | 1000.0 |
| Plassmann (1933) | 20009 | 200 | 100.0 |
| from Denis Roegel, 2013, | Technical reports, LORIA, Nancy, France, 2013. |
Pseudocode & Equations Section
more than one formula for 1) tables and 2) calculator shell
Babylonian multiplication rule a * b = ((a + b)/2)^2 - ((a - b)/2)^2 # used in calculator shell
conventional Western formula for quarter square multiplication tables
is a * b= (1/4)*(((a+b)**2) - ( (a-b)**2 ) ) # used in Western tables circa 1600 to 1950 CE.
quarter square multiplication formula for the tables
is x*y = <.25* (x+y)**2> * <.25* (x-y)**2>.
# recommended, avoids division by zero
half square multiplication formula for the tables
may be equivalent to x*y = 0.5* <.5* (x+y)**2> * <.5* (x-y)**2> # used in tables,
# recommended, avoids division by zero
modern extension to the Babylonian multiplication algorithm
from the binomial theorem is a*b = 0.5*{a+b)**2 -a**2-b**2} # considered for calculator shell
a * b = expr { $a * $b } # TCL math.c call for check answer
QS(N) = (1/4) * N**2 , or 0.25 * N**2, or int’ed [ int [ expr 0.25*$N**2]]
HS(N) = (1/2) * N**2 , or 0.5 * N**2, or int’ed [ int [ expr 0.5*$N**2 ]]
approximate Babylonian quadrilateral formula expr <((a+c)/2) *((b+d)/2) > (not exact!!!)
product of 50*40*30 using modern base_60 logarithms, # used in thinking pod
the sum of logs is expr { 0.95546+0.90096+0.830706} , 2.687126.
The antilog in base_60 is expr 60**2.687126= 59995.193.
For the tables, the int function is used to clip remainders to integers.
the precision function by [AM] is used occasionally, but not every time.
note: mental and undocumented components in the Babylonian multiplication methods.
# exponent/ logarithm expressions
log (sqrt (m)) = (1/2)*log (m)
log (crt (m)) = (1/3)*log (m)
log (sqrt (m)) = (1/2)*log (m)
(1/2) = log (sqrt (m)) / log (m)
(1/2) = log (sqrt (m)) - (m))
log (crt (m)) = (1/3)*log (m)
(1/3) = log (crt (m)) / log (m)
(1/3) = log (crt (m)) - (m))
(1/2) = log (sqrt (m)) / log (m)
(2/1) = log (m) / log (sqrt (m))
2 = log (m - (sqrt (m))
(3/1) = log (m) / log (crt (m))
3 = log (m - (crt (m))
N = log (m - (N’rt(m))
N+1 = log (m - ((N+1)’rt(m))
log2 defined as ln N / ln 2 ,
log2 N =~ 1.442695 * ln N
log2 N =~ 3.321928 * log10 N
From: Doctor Mitteldorf at MathForum & Uri Wilensky, MathForum
a(n) = sqrt of the nth square triangle number
then a(n) = ((3 + sqrt (8))^(n+1) - (3 - sqrt (8))^(n+1)) / 2 * sqrt (8)
should be integer, maybe?Appendix Code
Trial Calculator Shell
;# calculator is sticking on TCLLIB setup, TN calculation under trials
;# pretty print from autoindent and ased editor
;# Triangular Number Multiplication calculator V3
;# written on Windows 10 on TCL
;# working under TCL version 8.6
;# gold on TCL Club, 15jul2020
;# proc adapted from TCLLIB formatting
package require Tk
package require math::numtheory
package require math::constants
package require math::trig
package require math
;# package require math::combinatorics
;# namespace path {::tcl::mathop ::tcl::mathfunc math::numtheory }
namespace path {::tcl::mathop ::tcl::mathfunc math::numtheory math::trig math::constants }
set tcl_precision 17
frame .frame -relief flat -bg aquamarine4
pack .frame -side top -fill y -anchor center
set names {{} {aa integer quantity N1:} }
lappend names {bb integer quantity N2:}
lappend names {cc integer quantity N3: }
lappend names {dd integer quantity N4: }
lappend names {optional usually 1. :}
lappend names {answers: triangular number TN1 : }
lappend names {multiplication N1*N2 from TCL mathlib: }
lappend names {test slot >> multiplication N1*N2 from triangular numbers :}
foreach i {1 2 3 4 5 6 7 8} {
label .frame.label$i -text [lindex $names $i] -anchor e
entry .frame.entry$i -width 35 -textvariable side$i
grid .frame.label$i .frame.entry$i -sticky ew -pady 2 -padx 1 }
proc about {} {
set msg "Calculator for Triangular Number Multiplication V3
from TCL Club,
written on TCL "
tk_messageBox -title "About" -message $msg }
proc self_help {} {
set msg "Calculator for Triangular Number Multiplication V3
from TCL ,
;# self help listing
;# 4 givens follow.
1) aa integer N1
2) bb integer N2
3) cc integer N3
4) dd integer N4
;# some formulas pub. Elie de Joncourt, 1762, Netherlands
;# triangular number TN = N*(N+1)/2
;# sum of consecutive TN numbers are squares
;# TN <aa> + TN <aa+1> = square
;# Joncourt used TN to calculate square roots and cube roots
;# Joncourt used mult. aa * bb = <(aa+bb)**2 -aa**2 -bb**2>/2
;# term <(aa+bb)**2 -aa**2 -bb**2> is twice answer
;# binomial theorem >> a*b = 0.5*{(a+b)**2 -a**2-b**2}.
;# James Glaisher pub. TN formula from 1889
;# t. multiplication aa * bb = TN <aa-1> + TN <bb> - TN <aa-bb-1>
;# James Glaisher discussed TN and Quarter Square variants
;# Quarter Square >> a*b = <(a + b)**2 − (a − b)**2> * .25
;# another mult. formula m*n = TN(m+n) - TN(m) - TN(n)
;# used for division by reciprocal in flpating point.
;# The TCL procedures use base_10 in calculator.
;# Decimal fraction entries <1. clipped
;# to zero for TN calculations
;# For comparison, TCL code may include redundant paths & formulas.
;# The TCL calculator normally uses modern
;# units for convenience to modern users and textbooks.
;# Any convenient and consistent in/output units might be used
;# like inches, feet, nindas, cubits, or dollars to donuts.
;# Recommended procedure is push testcase and fill frame,
;# change first three entries etc, push solve,
;# and then push report. Report allows copy and paste
;# from console to conventional texteditor. For testcases
;# testcase number is internal to the calculator and
;# will not be printed until the report button is pushed
;# for the current result numbers.
;# This posting, screenshots, and TCL source code is
;# copyrighted under the TCL/TK 8.6 license terms.
;# Editorial rights retained under the TCL/TK license terms
;# and will be defended as necessary in court.
Conventional text editor formulas or grabbed from internet
screens can be pasted into green console.
Try copy and paste following into green screen console
set answer \[* 1. 2. 3. 4. 5. \]
returns 120
;# gold on TCL Club, 10jul2020 "
tk_messageBox -title "self_help" -message $msg }
proc precisionx {precision float} {
;# tcl:wiki:Floating-point formatting, <AM>
;# select numbers only, not used on every number.
set x [ expr {round( 10 ** $precision * $float) / (10.0 ** $precision)} ]
;# rounded or clipped to nearest 5ird significant figure
set x [ format "%#.5g" $x ]
return $x
}
proc swapper {target1 target2} {
;# not used now
;# if negative difference <target1 - target2>, possible use swapper
if { $target1 > $target2 } { return }
set keeper $target1
set target1 $target2
set target2 $keeper
return $target1 $target2
}
proc pyramid_d {hh bb} { return [ acotand [expr (.5*$bb/$hh) ]] }
proc pyra_d {hh bb} { return [ acotand [* .5 [/ $bb $hh] ]] }
;# pyramid_degrees 57.692 106.346 answer 47.334157521261254
;# adapted from tcl Stats 2011-05-22, arithmetic mean <RLE>
;# ::math::triangular_number --
;#
;# Return the triangular_number for one,two, or more numbers
;# defined as quantity per price
;#
;#
;# Arguments:
;#
;# args values are one, two, or more given numbers
;#
;# Results: triangular_number
;# works for positive numbers, negative numbers,
;# and mixed positive & negative numbers.
;# arg of zero returns zero
;# arg of null returns zero
;# filter foreach drops irregular zero elements from argument
proc ::math::triangular_number { args} {
set sum 0.
set N [ expr { [ llength $args ] } ]
if { $N == 0 } { return 0 }
#if { $N == 1 || [ lindex $args 0 ] == 0 } { return 0 }
#if { $N == 1 || [ lindex $args 0 ] == 0 } { return 1 }
set res {};set counter2 0;
;# filter foreach drops irregular zero elements
foreach item $args {
if {$item != 0 } {
incr counter2 1;
#set item [ expr { abs($item)} ]
lappend res $item } }
set counter 0
foreach val $res {
#if { $val > 1. } { lappend listerx [expr { $val*($val+1.)*.5}]}
if { $val > .9999999 } { lappend listerx [expr { $val*($val+1.)*.5}]}
#if { $val < 1. && $val > -1. } {lappend listerx "*" }
if { $val < 1. && $val > -1. } {lappend listerx 0 }
if { $val < -1. } {
set val [ expr { abs($val)} ]
lappend listerx [expr { -1.* $val*($val+1.)*.5}]}
incr counter 1
}
set triangular_number1 [ lindex $listerx 0 ]
;# return $triangular_number1
return $listerx
}
;# reciprocal_division trial procs
;# used alternative multiplication_tn formula
;# multiplication related procs here reset
;# and return floating point fp.
proc trinity {aa} {expr { $aa*($aa+1.)*.5}}
;# trinity proc here resets and returns floating point fp.
;# Usage trinity 7 -> 28.0 ;# Usage trinity 5 -> 15.0
;# Usage trinity 3 -> 6.0 ;# Usage trinity 2 -> 3.0
proc beauty_multiplication_tn { aa bb } {return [+ [trinity [+ $aa $bb] ] [* -1. [trinity $aa]] [* -1. [trinity $bb]] ]}
;# Usage beauty_multiplication_tn 7 7 -> 49.0 ;# returns floating point fp.
;# Usage beauty_multiplication_tn 999999.0 777777.0 -> 777776222223.0 fp.
;# Usage beauty_multiplication_tn 999999.0 0.5 -> 499999.5 fp
;# reciprocal_division is m X 1./r in floating point
proc reciprocal_division_tn { m r } {
set n [expr {1./ $r} ];
return [ expr { ($m+$n)*($m+$n+1.)/2. -$m*($m+1.)/2. - $n*($n+1.)/2.}] }
;# m >= 1, r > = 1, {1./ $r} = $n, $n is reciprocal r in floating point
;# reciprocal proc in fp appears to be off
;# by one part in 10E6.
;# Usage reciprocal_division_tn 4 .5 -> 2
;# Usage reciprocal_division_tn 999 .5 -> 499.5
;# Usage reciprocal_division_tn 1000000 .5 -> 500000.0
;# Usage reciprocal_division_tn 999999 .5 -> 499999.5
;# Usage reciprocal_division_tn 1000000000 .5 -> 499999999.625
;# various testcases on triangular_number proc
;# puts [::math::triangular_number 1 2 3 4 ]
;# answer 1.0 3.0 6.0 10.0 "
;# puts [ ::math::triangular_number 1 2 3 3 ]
;# answer 1.0 3.0 6.0 6.0
;# ::math::triangular_number 3 4 7 9
;# answer 6.0 10.0 28.0 45.0 , correct
;# ::math::triangular_number 3 6 5 7
;# answer 6.0 21.0 15.0 28.
;# puts " for (::math::triangular_number 1)
;# returns " for 1 "
;# ::math::triangular_number 0
;# arg 0 returns 0 zero, correct.
;# addition dated 24sep2020
;# added filter foreach to remove zero's
;# irregular zeros,
;# test on fractions 0.1 0.2 0.3 0.4
;# returns 0 0 0 0 , correct
;# test on fractions and zero 0.1 0.2 0.0 0.4
;# returns 0 0 0 , correct
proc trinity_product2 {aa bb} {return [+ [trinity [- $aa 1.0] ] [trinity $bb] [* -1.0 [trinity [- $aa $bb 1.0 ] ]]]}
proc trinity_square {aa} {return [+ [trinity [+ $aa $aa] ] [* -1. [trinity $aa]] [* -1. [trinity $aa]] ]}
proc trinity_cube {aa} {
set term1 [ trinity $aa ]
set term2 [ trinity [- $aa 1 ]]
set res [ expr { $term1**2 - $term2**2 } ]
return $res }
proc calculate { } {
global answer2
global side1 side2 side3 side4 side5
global side6 side7 side8
global testcase_number
incr testcase_number
set side1 [* $side1 1. ]
set side2 [* $side2 1. ]
set side3 [* $side3 1. ]
set side4 [* $side4 1. ]
set side5 [* $side5 1. ]
set side6 [* $side6 1. ]
set side7 [* $side7 1. ]
set side8 [* $side8 1. ]
set triangular_number1 1.
set triangular_number2 1.
set triangular_number_product 1.
;# set triangular_number_product [ ::math::triangular_number_conversion 5 ]
set integer1 [ expr { int($side1)} ]
set integer2 [ expr { int($side2)} ]
set integer3 [ expr { int($side3)} ]
set integer4 [ expr { int($side4)} ]
set triangular_number1 1
set triangular_number2 1
set triangular_number1 [ expr { $integer1 * ($integer1 + 1 )*.5 } ]
set triangular_number2 [ expr { $integer2 * ($integer2 + 1 )*.5 } ]
set triangular_number_product 999999
set side5 [::math::triangular_number $integer1 $integer2 $integer3 $integer4]
set side6 $triangular_number1
set side7 [* $side1 $side2 ]
;# set side8 [+ $triangular_number1 $triangular_number2]
;# set side8 [trinity_product $side1 $side2 ]
;# set side8 [+ [trinity $side1] [trinity $side2] ]
set side8 [+ [trinity [- $integer1 1.0] ] [trinity $integer2] [* -1.0 [trinity [- $integer1 $integer2 1.0 ] ]]]
puts " $side5 [trinity [- $integer1 1.0] ] [trinity $integer2] [* -1.0 [trinity [- $integer1 $integer2 1.0 ] ]] $side8 "
set boo8 [+ [trinity [- $side1 1.0] ] [trinity $side2] [* -1.0 [trinity [- $side1 $side2 1.0 ] ]]]
puts " $boo8 $side1 $side2 [+ [trinity [- $side1 1.0] ] [trinity $side2] [* -1.0 [trinity [- $side1 $side2 1.0 ] ]]] "
}
proc fillup {aa bb cc dd ee ff gg hh} {
.frame.entry1 insert 0 "$aa"
.frame.entry2 insert 0 "$bb"
.frame.entry3 insert 0 "$cc"
.frame.entry4 insert 0 "$dd"
.frame.entry5 insert 0 "$ee"
.frame.entry6 insert 0 "$ff"
.frame.entry7 insert 0 "$gg"
.frame.entry8 insert 0 "$hh"
}
proc clearx {} {
foreach i {1 2 3 4 5 6 7 8 } {
.frame.entry$i delete 0 end } }
proc reportx {} {
global side1 side2 side3 side4 side5
global side6 side7 side8
global testcase_number
console show;
console eval {.console config -bg palegreen}
console eval {.console config -font {fixed 20 bold}}
console eval {wm geometry . 40x20}
console eval {wm title . " Triangular Number Multiplication V2 Report , screen grab and paste from console 2 to texteditor"}
console eval {. configure -background orange -highlightcolor brown -relief raised -border 30}
puts "%|table $testcase_number|printed in| tcl format|% "
puts "&| quantity| value| comment, if any|& "
puts "&| $testcase_number:|testcase_number | |&"
puts "&| $side1 :|aa integer quantity N1: | |&"
puts "&| $side2 :|bb integer quantity N2: | |& "
puts "&| $side3 :|cc integer quantity N3: | |& "
puts "&| $side4 :|dd integer quantity N4: | |&"
puts "&| $side5 :|optional: | |&"
puts "&| $side6 :|triangular number TN1 | |&"
puts "&| $side7 :|multiplication from TCL mathlib: | |&"
puts "&| $side8 :|test slot >> multiplication TN1*TN2 from triangular numbers : | |&"
puts "&| [::math::triangular_number 5 2 3 4 ] |test slot >> TN1*TN2 : | |&"
puts "&| [reciprocal_division_tn $side1 $side2] |reciprocal_division_tn test slot N1= $side1 N2= $side2 >> m * (1/r) : | fp |&"
puts "&| [ expr { $side1*(1./$side2) }] |reciprocal math library check N1= $side1 N2= $side2 >> m * (1/r) : | fp |&"
puts "&| beauty_multiplication_tn $side1 X $side2 returns [beauty_multiplication_tn $side1 $side2] |test slot >> beauty mult. formula $side1 $side2 : | |&"
puts "&| expr $side1 X $side2 returns [expr {$side1 * $side2} ] |test slot >> mathlib check mult $side1 X $side2 : | |&"
puts "&| trinity_square $side1 returns [trinity_square $side1 ] |test slot >> square formula $side1 : | |&"
puts "&| expr $side1 X $side1 returns [expr {$side1 * $side1} ] |test slot >> mathlib check square $side1 : | |&"
puts "&| trinity_cube $side1 returns [trinity_cube $side1 ] |test slot >> cube formula $side1 : | |&"
puts "&| mathlib N**3 for $side1 returns [ expr {$side1**3}] |test slot >> mathlib check $side1 : | |&"
puts "&| TN <1 2 0 4 > returns [::math::triangular_number 1 2 0 4 ] |test slot >> TN1 TN2 : | |&"
puts "&| TN <1 2 0 0 > returns [::math::triangular_number 1 2 0 0 ] |test slot >> TN1 TN2 : | |&"
puts "&| TN <1 2 -3 4 > returns [::math::triangular_number 1 2 -3 4 ] |test slot >> TN1 TN2 : | |&"
puts "&| TN <10 20 30 40> returns [::math::triangular_number 10 20 30 40 ] |test slot >> TN1 TN2 : | |&"
puts " pyramid [ pyra_d 57.692 106.346 ] "
}
frame .buttons -bg aquamarine4
::ttk::button .calculator -text "Solve" -command {set side5 1.; calculate }
::ttk::button .test2 -text "Testcase1" -command {clearx;fillup 1. 2. 3.0 4. 1.0 1. 2.0 2.0}
::ttk::button .test3 -text "Testcase2" -command {clearx;fillup 3.0 4.0 7.0 9.0 1.0 6.0 12. 12. }
::ttk::button .test4 -text "Testcase3" -command {clearx;fillup 3.0 6. 5.0 7.0 1.0 6.0 18.0 18. }
::ttk::button .clearallx -text clear -command {clearx }
::ttk::button .about -text about -command {about}
::ttk::button .self_help -text self_help -command {self_help }
::ttk::button .cons -text report -command { reportx }
::ttk::button .exit -text exit -command {exit}
pack .calculator -in .buttons -side top -padx 10 -pady 5
pack .clearallx .cons .self_help .about .exit .test4 .test3 .test2 -side bottom -in .buttons
grid .frame .buttons -sticky ns -pady {0 10}
. configure -background aquamarine4 -highlightcolor brown -relief raised -border 30
wm title . "Triangular Number Multiplication Calculator V3"appendix : TCL console Script on TN Tables
# pretty print from autoindent and ased editor
# Quarter Squares and Triangular Numbers Tables
# written on Windows XP on TCL
# working under TCL version 8.6
# gold on TCL, 10jul2020
wm title . " Quarter Squares Tables"
namespace path {::tcl::mathop ::tcl::mathfunc}
set tclprecision 17
console show
console eval {.console config -bg palegreen}
console eval {.console config -font {fixed 20 bold}}
console eval {wm geometry . 40x20}
console eval {wm title . " Quarter Squares Tables , cut and paste from console 2"}
console eval {. configure -background orange -highlightcolor brown -relief raised -border 30}
proc precisionx {precision float} {
# tcl:wiki:Floating-point formatting, <AM>
# select numbers only, not used on every number.
set x [ expr {round( 10 ** $precision * $float) / (10.0 ** $precision)} ]
# rounded or clipped to nearest 5ird significant figure
set x [ format "%#.5g" $x ]
return $x
}
proc list_quarter_squares { aa bb} {
for {set i $aa} {$i<=$bb} {incr i} {
puts " &| $i | [ precisionx 3 [ int [* .25 $i $i] ] ] | |& "; }
return 1}
proc list_half_squares { aa bb} {
for {set i $aa} {$i<=$bb} {incr i } {
puts " &| $i | [ precisionx 3 [ int [* .5 $i $i] ] ] | |& ";
puts " &| [+ $i .5 ] | [ precisionx 3 [ int [* .5 [+ $i .5] [+ $i .5] ] ] ] | |& ";}
return 1}
proc list_binomial_theorem { aa bb} {
for {set i $aa} {$i<=$bb} {incr i} {
set a $i
set b $i
puts " &| $i | [ precisionx 3 [expr { 0.5*(($a+$b)**2-$a**2-$b**2) } ] ] | |& "; }
return 1}
proc list_triangular_numbers { aa bb} {
for {set i $aa} {$i<=$bb} {incr i} {
puts " &| $i | [ precisionx 3 [ int [* .5 $i [+ $i 1]] ] ] | |& "; }
return 1}
set testcase_number 1
puts "%|Table $testcase_number: Quarter Squares Tables |printed in| tcl format|% "
puts "%|N | int <N*N*.25> | comments if any|% "
list_quarter_squares 0 18
set testcase_number 2
puts "%|Table $testcase_number: Half Squares Tables |printed in| tcl format|% "
puts "%|N | int <N*N*.5> | comments if any|% "
list_half_squares 0 20
set testcase_number 3
puts "%|Table $testcase_number: Binomial_Theorem Squares Tables |printed in| tcl format|% "
puts "%|a | a*a from subbing a*b = 0.5*(a+b)**2 -a**2-b**2) | comments if any |% "
list_binomial_theorem 0 20
set testcase_number 4
puts "%|Table $testcase_number: Triangular Numbers Tables |printed in| tcl format|% "
puts "%|a | subbing a*(a+1)*.5 number series | comments if any |% "
list_triangular_numbers 0 20
# gold on TCL Club, 10jul;2020
# This posting, prose, screenshots, and TCL source code is
# copyrighted under the TCL/TK license terms.
# Editorial rights and disclaimers retained
# under the TCL/TK license terms
# and will be defended as necessary in court.
# end of file
appendix, Console script on Triangular Numbers List
# written on Windows XP on TCL
# working under TCL version 8.6
# gold on TCL, 10jul2020
wm title . " Triangular Numbers TN List "
console show
console eval {.console config -bg palegreen}
console eval {.console config -font {fixed 20 bold}}
console eval {wm geometry . 40x20}
console eval {wm title . " Triangular Numbers TN List , cut and paste from console 2"}
console eval {. configure -background orange -highlightcolor brown -relief raised -border 30}
# Babylonian quasi_square2 is n*(n+1),
proc list_quasi_square2 { aa bb} { for {set i 1} {$i<=$bb} {incr i} {lappend boo [* 1. $i ] [* $i [+ $i 1]]};return $boo}
# usage, list_quasi_square2 1 10
# 1.0 2 2.0 6 3.0 12 4.0 20 5.0 30 6.0 42 7.0 56 8.0 72 9.0 90 10.0 110
puts " [ list_quasi_square2 1 10 ] "
# triangular_number_ref_quasi_square3 is n*(n+1)/2,
proc triangular_numbers_ref_quasi_square3 { aa bb} { for {set i 1} {$i<=$bb} {incr i} {lappend boo [* 1. $i ] [* $i [+ $i 1] .5 ]};return $boo}
# usage, list_quasi_square2 1 10
# 1.0 2 2.0 6 3.0 12 4.0 20 5.0 30 6.0 42 7.0 56 8.0 72 9.0 90 10.0 110
puts " [ triangular_numbers_ref_quasi_square3 1 10 ] "Problem Solved
gold 8/4/2020. Statements below TCLLIB library on ActiveState 8.6.
# pretty print from autoindent and ased editor
# Triangular Square Numbers V2
# console program
# written on Windows 10 on TCL
# working under TCL version 8.6
# gold on TCL Club, 15jul2020
package require Tk
package require math::numtheory
package require math::constants
package require math
namespace path {::tcl::mathop ::tcl::mathfunc math::numtheory math::constants }
# test includes invoke TCLLIB library
set tcl_precision 17
console show
console eval {.console config -bg palegreen}
console eval {.console config -font {fixed 20 bold}}
console eval {wm geometry . 40x20}
console eval {wm title . " Triangular Number Multiplication V2 Report , screen grab and paste from console 2 to texteditor"}
console eval {. configure -background orange -highlightcolor brown -relief raised -border 30}
proc precisionx {precision float} {
# tcl:wiki:Floating-point formatting, <AM>
# select numbers only, not used on every number.
set x [ expr {round( 10 ** $precision * $float) / (10.0 ** $precision)} ]
# rounded or clipped to nearest 5ird significant figure
set x [ format "%#.5g" $x ]
return $x
}
proc ::math::sum_triangular_number2 { args} {
set sum 0.
set N [ expr { [ llength $args ] } ]
if { $N == 0 } { return 0 }
#if { $N == 1 || [ lindex $args 0 ] == 0 } { return 0 }
set res {};set counter2 0;
# filter foreach drops irregular zero elements
foreach item $args {
if {$item != 0 } {
incr counter2 1;
#set item [ expr { abs($item)} ]
lappend res $item } }
set counter 0
foreach val $res {
lappend listerx [expr { $val*($val+1.)*($val+2.)/6. }]
incr counter 1
}
set triangular_number1 [ lindex $listerx 0 ]
# return $term1
return $listerx
}
proc sum_triangular_number {nn} { return [ expr { $nn*($nn+1.)*($nn+2.)/6. } ]}
# sum_triangular_number series 1, 4,m
puts " sum_triangular_number 1 = [ sum_triangular_number 1. ] "
puts " sum_triangular_number 2 = [ sum_triangular_number 2. ] "
puts " sum_triangular_number 3 = [ sum_triangular_number 3. ] "
puts " expanded proc for sum_triangular_number 1 = [ precisionx 3 [ ::math::sum_triangular_number2 1. ] ]"
::math::constants::constants radtodeg degtorad
::math::constants::constants onethird
::math::constants::constants huge
puts "OneThird = $onethird huge = $huge";
puts " math choose statements [::math::choose 10 2 ] [math::choose [+ 3 1 ] 2 ] [math::choose [+ 10 1 ] 2 ] "
# end of file output sum_triangular_number 1 = 1.0 sum_triangular_number 2 = 4.0 sum_triangular_number 3 = 10.0 expanded proc for sum_triangular_number 1 = 1.0000 OneThird = 0.33333333333333331 huge = 1.7976931348623157e+308 math choose statements 45 6 55
Hidden Comments Section
Please place any comments here with your wiki MONIKER and dates, Thanks,gold12JUL2020
gold Removed copyright.