A little math language revisited
Arjen Markus (7 may 2004) Recent interest in the possibilities of using Tcl for numerical analysis, brought back the page A little math language. I decided to explore this a bit further ... It is not complete yet, but you get the drift, I think, from the examples/test code.
AM (10 may 2004) One thing I'd like to add is support for such mathematical tools like:
y = lim x->inf x*(atan(2x)-atan(x)) y = int x=0 to 1 exp(x**2) y = deriv x=0 atan(x+sqrt(x))
(oh, none of these have any practical value as far as I am concerned, I just made them up whilst typing ...). This did bring me to consider a Simple method for computing mathematical limits.
AM (8 july 2004) A slight update to the original script: I added the possibility to use array elements. This does assume a fixed list of math functions in [expr] and it does not yet work with:
x(i+1) = x(i) * a
and such ... (Makes me wonder: how does Tcl handle:
set i 1
set a [expr {$b($i-1)+$b($i)]assuming b(0) and b(1) are defined ... After all these years still some puzzles to solve and a little interactive tclsh session led to the answer:
% set b(0) 1
1
% set b(1) 2
2
% set i 1
1
% set a [expr {$b($i-1)+$b($i)}]
can't read "b(1-1)": no such element in array
% )
The reason I added support for array elements is that Shen-Yeh Chen, who is working on a package called OpTcl - optimisation with Tcl - asked for this. For his customers, Tcl is a way to use the optimisation package (written in Fortran) without having to program in C or Fortran themselves.
Because statements like
G1=0.52*X1*X1-3.12*X1+0.72*X1*X2-21.6*X2+0.73*X2*X2-3.68 G1=G1/100.0 G2=225.0-pow(X1+30.0,2.0)-pow(X2-30.0,2.0) G2=G2/225.0
are much more natural for them than the ordinary Tcl syntax, this little script helps a lot.
(His project provides me with a nice opportunity to further develop my Ftcl library that makes the combination of Fortran and Tcl possible - see: Combining Fortran and Tcl in one program).
Code
# mathlang.tcl --
# Provide commands that allow a more usual mathematical syntax:
#
# mathfunc {x} {
# sinc = sin(x)/x if x != 0
# sinc = 0 otherwise
# }
# math {
# a = x*x + y*y
# }
#
# Still to do: mathfunc
#
# (7 july 2004) Small improvement:
# recognise array elements
#
namespace eval ::mathsyntax {
namespace export math
variable cached_calcs {}
variable func_names \
{abs acos asin atan atan2 ceil cos cosh double
exp floor fmod hypot int log log10 pow rand round
sin sinh sqrt srand tan tanh wide}
}
# ToExpr --
# Transform an expression to the form expr wants
# Arguments:
# expression A right-hand side of an assignment
# Result:
# Valid Tcl expression
#
proc ::mathsyntax::ToExpr { expression } {
variable func_names
set rhs [string map {" " ""} $expression]
set indices [regexp -inline -all -indices {[a-zA-Z][a-zA-Z0-9_]*} $rhs]
set offset 0
foreach idx $indices {
foreach {start stop} $idx {break}
set start [expr {$start+$offset}]
set stop [expr {$stop+$offset}]
set next [expr {$stop+1}]
if { [string index $rhs $next] != "(" } {
set char [string index $rhs $start]
set rhs [string replace $rhs $start $start "\$$char" ]
incr offset
} else {
set char [string index $rhs $start]
set name [string range $rhs $start $stop]
if { [lsearch $func_names $name] < 0 } {
set rhs [string replace $rhs $start $start "\$$char" ]
}
}
}
return $rhs
}
# Transform --
# Transform a series of mathematical expressions into Tcl code
# Arguments:
# id ID to use
# calc One or more mathematical assignments
# Result:
# None
# Side effects:
# A private procedure is created
# Note:
# No conditions yet
#
proc ::mathsyntax::Transform { id calc } {
set calc [split $calc "\n"]
set body {"uplevel 2 \{"}
foreach assign $calc {
set assign [string trim $assign]
if { $assign != "" } {
regexp {([a-zA-Z][a-zA-Z0-9_()]*) *= *(.*)} $assign ==> lhs rhsfull
#
# Is there a condition?
#
set cond1 [string first " if" $rhsfull]
# PM: set cond2 [string first " otherwise" $rhsfull]
set cond ""
if { $cond1 > 0 } {
set rhs [string range $rhsfull 0 [expr {$cond1-1}]]
set cond [string range $rhsfull [expr {$cond1+3}] end]
lappend body "if { [ToExpr $cond] } \{"
} else {
set rhs $rhsfull
}
# If the left-hand side refers to an array element,
# we need to add a dollar-sign
#
set lhs [string map {"(" "($"} $lhs]
#
# Prepare the assignment
#
set rhs [ToExpr $rhs]
lappend body "set $lhs \[expr {$rhs}\]"
if { $cond != "" } {
lappend body "\}"
}
}
}
lappend body "\}"
proc Cached$id {} [join $body "\n"]
}
# math --
# Allow mathematical expressions inside Tcl code
# Arguments:
# calc One or more mathematical assignments
# Result:
# None
# Side effects:
# As the code is executed in the caller's scope, variables
# in the calling procedure are set
# The code is transformed into a procedure that is cached
#
proc ::mathsyntax::math { calc } {
variable cached_calcs
set id [lsearch $cached_calcs $calc]
if { $id < 0 } {
lappend cached_calcs $calc
set id [expr {[llength $cached_calcs]-1}]
Transform $id $calc
}
::mathsyntax::Cached$id
}
#
# Simple test
#
namespace import ::mathsyntax::math
set a 1
set b 1
set c ""
set d ""
set sinc ""
math {
c = a + b
d = a + cos(b+c)
}
puts "$c $d"
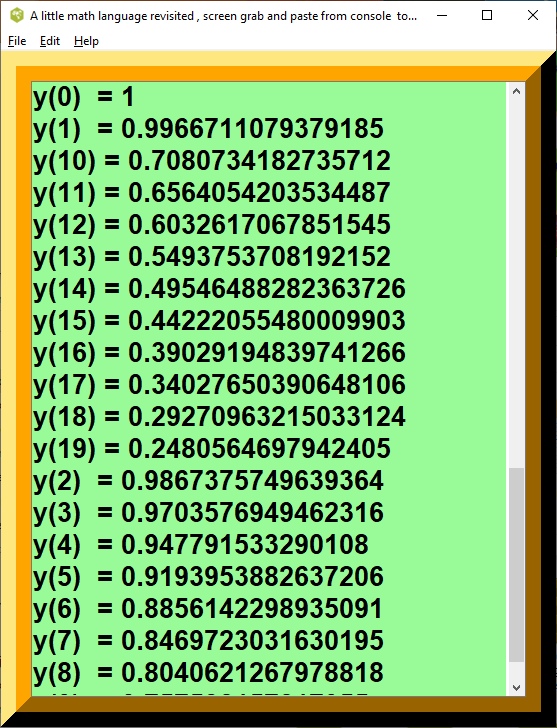
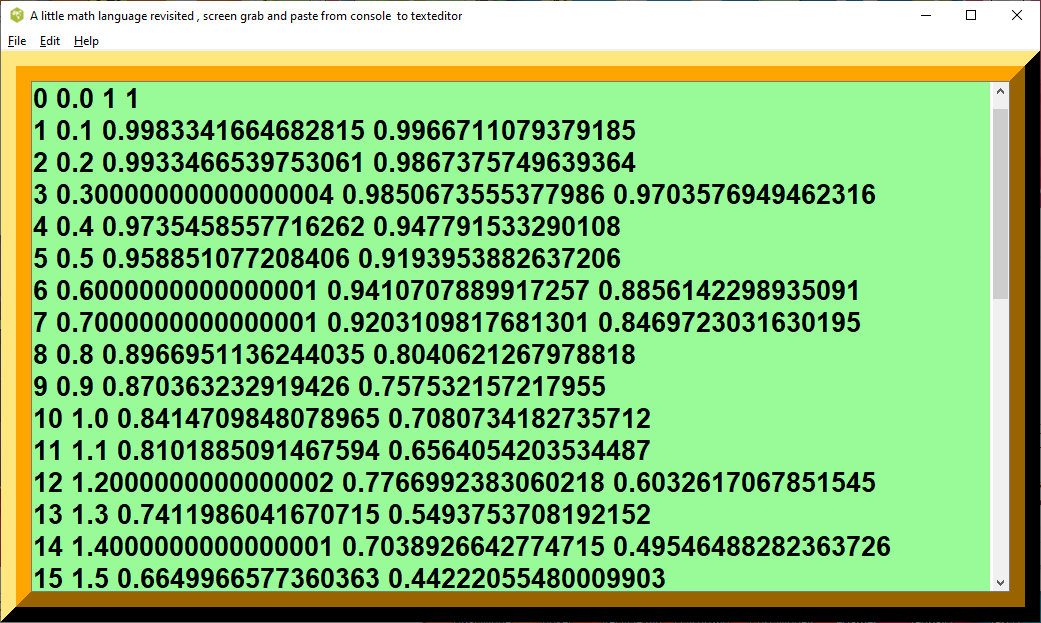
for {set i 0} {$i < 20} {incr i} {
math {
x = 0.1*i
sinc = 1 if x == 0
sinc = sin(x)/x if x != 0
y(i) = sinc*sinc
}
puts "$i $x $sinc $y($i)"
}
#
# Just to check
#
parray yDiscussion
FM maybe we should return a list, because it should be sometime interesting to get all the values. To illustrate, here is what how I did that :
I added :
variable Res [list]
in namespace eval ::mathsyntax { ... }
In proc ::mathsyntax::Transform { id calc } { ... }
set calc [split $calc "\n\;"]
instead of : set calc [split $calc "\n"]
lappend body "lappend ::mathsyntax::Res \[set $lhs \[expr {$rhs}\]\]"instead of lappend body "[[set $lhs [[expr {$rhs}\]\]"
Adding at the end of proc ::mathsyntax::math { calc } { ... }
lindex $::mathsyntax::Res
## to test :
pack [canvas .c]
.c create line {*}[set L [list]; for {set i -200} {$i < 200} {incr i} {
math {
x = 0.1*i
sinc = 1 if x == 0
sinc = sin(x)/x if x != 0
}
lappend L {*}[math {X=200+10*x;Y=200-100*sinc}]
}; set L]gold9/20/2020, added appendix and pix, but above text and code unchanged.
Figure 1. A little math language revisited screenshot one
Figure 2. A little math language revisited screenshot two
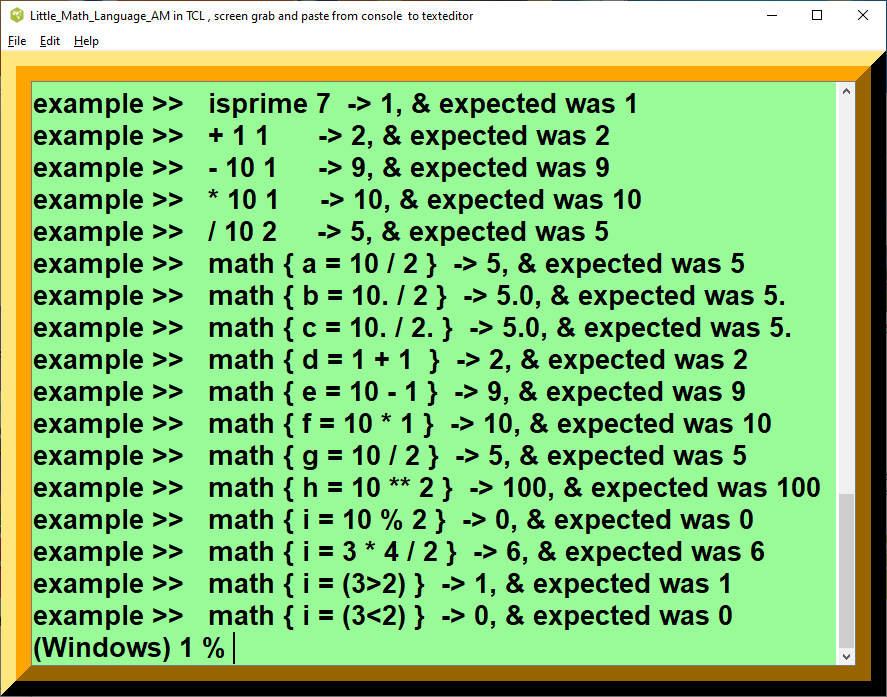
figure 3. A little math language revisited screenshot 3
References
- A little math language revisited
- Playing with Recursion by RS
- Functional Programming
- recursion
- func
- John McCarthy: A basis for a mathematical theory of computation, in:
- Computer Programming and Formal Systems.
- P.Braffort, D.Hirschberg (ed.), Amsterdam:North Holland 1963,
- several versions, archived pdf [L1 ]
- McCarthy’s LISP and Basis for Theory of Computation, archived pdf[L2 ]
- en.wikipedia.org search on <John McCarthy computer> [L3 ]
- John McCarthy at Stanford web site, archived [L4 ]
- Towards a Mathematical Science of Computation, J. McCarthy,
- Computer Science Department,Stanford University, archived pdf [L5 ]
- Elephant 2000: A Programming Language Based on Speech Acts
- John McCarthy, Stanford University, archived [L6 ]
- Elephant input and output statements are characterized
- as speech acts and programs, which
- can refer directly to the past.
- Elephant proposal contains summary
- on McCarthy mathematical theory of computation
- King that learns? A Program That Learns
- upvar sugar
- Salt and Sugar
- Math sugar
- A little math language
- args
- RS
- LV
- Radical Language Modification
- Functional Programming
- Custom curry
- Playing with recursion
- Modeling COND with expr
- Sample Math Programs
- Professor Frisby's Mostly Adequate Guide to Functional Programming [L7 ]
- expr shorthand for Tcl9
- Steps towards functional programming
- Tacit programming
- The fortran call statement appeared in Fortran2 (1958). example of call exit, fortran 4
- Thocp code, http://www.thocp.net/software/languages/fortran.htm
- Natural User Interface
- Natural Languages category
- Game kingdom of strategy
- wikipedia.org wiki The_Sumerian_Game
- Find all words
- Things German
- How to synthesize a query
- Writing Tk programs so that the user can extend or interact with them without modifying the application
- Ruslish
- Accumulator Generators
- Accumulator Generator
- Whadjasay
- disassemble byte code [L8 ]
- One Liners Programs Compendium [L9 ]
- One Liners
- Oneliner's Pie in the Sky
- Ref. WIKI BOOKS, Tcl_Programming_Introduction, [L10 ]
- Book Section contrasts one liners programs
- versus traditional procedural approach,
- Multiple Wiki Books on TCL programming [L11 ]
- if
- New Control Structures
- Kernighan and Pike: The practice of programming
Hidden Comments Section
Please include your wiki MONIKER and date in your comment Thanks, gold 12Aug2020
| Category Numerical Analysis | Category Toys | Category Calculator | Category Mathematics | Category Example | Toys and Games | Category Games | Category Application | Category GUI |