Collatz_Sequences (3*N+1) V4
This page is under development. Comments are welcome, but please load any comments in the comments section at the bottom of the page. Please include your wiki MONIKER and date in your comment with the same courtesy that I will give you. Aside from your courtesy, your wiki MONIKER and date as a signature and minimal good faith of any internet post are the rules of this TCL-WIKI. Its very hard to reply reasonably without some background of the correspondent on his WIKI bio page. Thanks, gold 3/27/2024
- Title: Collatz_Sequences (3*N+1) V4
- Preface
- Introduction
- Modified Collatz_Sequence
- Piece-wise Curve Fit to the Terminus of Collatz_Sequence
- Gamblers_Ruin_Expectation, Probability, and Bound Limits on Collatz_Sequences
- Bounds and Limits on the Collatz_Sequences help define the CS. trajectory and envelope
- Body : Comments and Rewrite by HE
- Easy Eye Concept for Windows10 Console
- Test Suite
- Pushbutton Operation
- Insights into the Collatz Infinite Sequences
- Possible Uses of Collatz Sequences Conjecture
- Gist and Outline on the applications on the Collatz Sequences
- Conclusions
- References:
- References on Turing machines:
- Screenshots Section
- figure 1a. Screenshot, Collatz_Sequences_(3*N+1) _screenshot
- figure 1b. Screenshot, Collatz_Sequences_screenshot_gui
- figure 2. Collatz_Sequences_double_collatz
- figure 3. [Collatz_Sequences_residuals
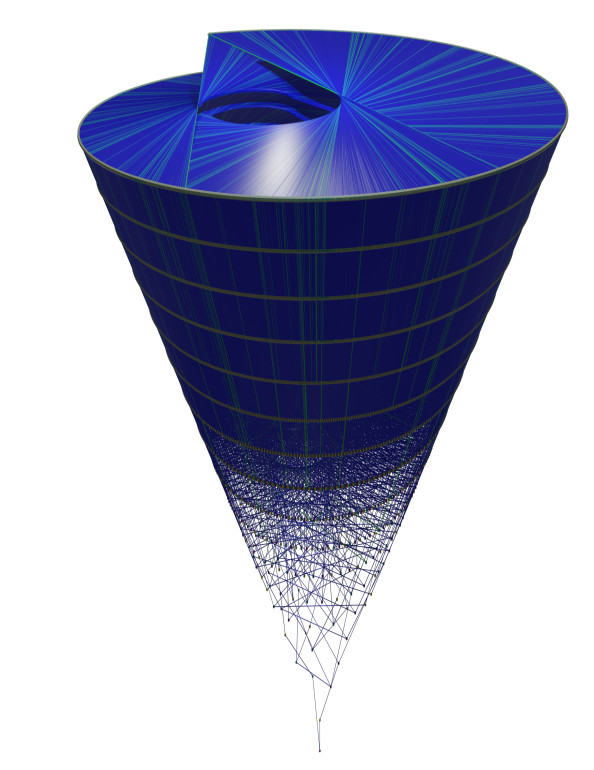
- figure 4. Collatz_Sequences (3*N+1) Collatz cone side view , credit Idriss J. Aberkane
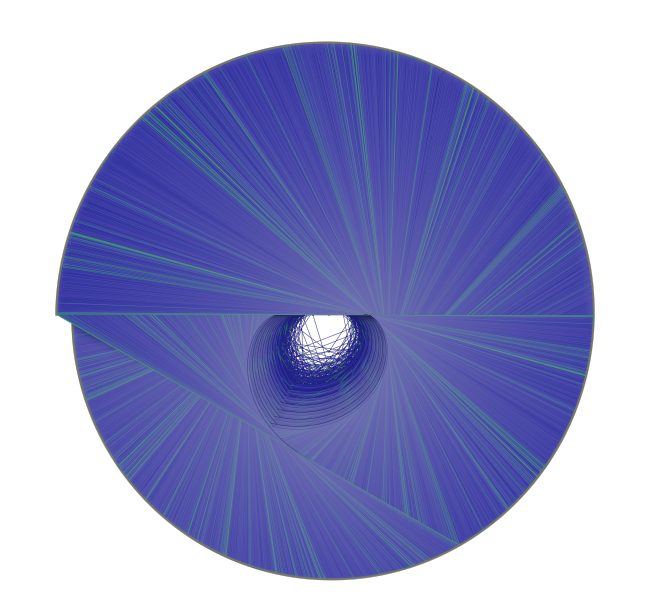
- figure 5. Collatz_Sequences (3*N+1) Collatz cone top view , credit Idriss J. Aberkane
- Testcases Section
- Testcase 1, Partial Collatz_Sequences
- Testcase 2, Collatz_Sequence for integer 7 from Windows10 gui
- Testcase , Collatz_Sequence for integer 27 from Windows10 gui
- Testcase , Collatz_Sequence for integer 10 from Windows10 gui
- Testcase , Collatz_Sequence for integer 7 from Windows10 gui
- Testcase , modified__Sequence for integer 10 from Windows10 gui
- Testcase , modified__Collatz_Sequence for integer 10 from Windows10 gui
- Testcase , Partial Collatz_Sequence for integer 7 from Windows10 gui
- Appendix TCL programs and scripts
- Pretty Print Version
- Main Deck
- Pseudocode and Equations Section
- Hidden Comments Section
- Hidden Comments Section
Title: Collatz_Sequences (3*N+1) V4
Preface
gold 3/27/2024 updated. In 1937, Lothar Collatz conjectured that the Collatz Sequence of any positive number would begin repeating and coalesce to 1. The dependency of the Collatz Sequence gui graphical user interface on the ActiveState TCL and Windows10 Console TK widget is noted on the page title and source code. Many thanks to HE for comments and feedback on Unix side. In terms of use on other TCL platforms, I am interested in proving and petitioning the Collatz Sequences code to the TCLLIB. The main task for me was getting the Tcllib ticket on Collatz Sequences out the door!!! I believe that the proposed implementation of the Collatz_Sequences functions in the Tcllib will accommodate both the Windows10 and UNIX users of TCL. Note: Many thanks to arjen & Andreas Kupries for the heavy lifting Tcllib. I have added the offline feedback and feedback png's. As one can appreciate, we are approaching the asymptotic limit of high school algebra, some 50 years ago. Thanks to all for your comments.
gold Update 3/2/2024. This page on developing pseudocode examples and one line procedures is not a replacement for the current Tcl core and Tcllib, which is much improved since Tcl version 4, and other <faster> language constructs. math ops, Tcllib routines, and other compiled routines can reduce the cost of big-data tasks by about 1/3. The time savings of the core and Tcllib are not always obvious on small quantities of data, like 4 or 5 numbers. Performance of one-line programs may suffer degradation due to lengthy recursion calls, and may be limited by constraints on recursion. Dependence on math operator notation, helper procedures, math check examples, degradation due to lengthy recursion calls, and special library functions should be noted in the comment lines.
Introduction
gold updated 9/29/2021. Here are TCL calculations on the Collatz Sequences. The Collatz Sequences were named after German mathematician Lothar Collatz (1910–1990). Collatz conjectured that the Collatz Sequence of any positive number would begin repeating and coalesce to 1. The proc collatz_sequence was substantially rewritten by HE and replaced in the main deck with good valuable comments, which I will have to chew on. Primarily, I am interested in petitioning the code for Collatz_Sequences and modified_Collatz_Sequences to the TCLLIB. Many thanks to HE for comments and feedback.
The collatz_sequence proc returns the partial collatz_sequence from positive integers. This collatz_sequence proc can easily generate an endless loop without a conditional stop. In fact, the known collatz_sequences are an endless list or repetitive string of integers. The iteration or calculation step limit is a stop or limit to iteration. By custom, the end of the partial collatz_sequence is 1 or start of repetition. For example, the collatz_sequence for integer 5 would be < 5 16 8 4 2 1 4 2 1 4 2 1 4 2 1 4 2 1 4 2 1 4 ...> The proc with entry 5 is intended to report the partial collatz_sequence of < 5 16 8 4 2 1 >. In the literature, the sequence < ... 16 8 4 2 1 ... > is called the tail on the known collatz_sequences. Many of the known collatz_sequences coalize or boil down to end and tail in < ... 16 8 4 2 1 ... > , so it is somewhat counter intuitive to me that various positive integers have the same terminus in their collatz_sequence.
The logic order here for Collatz_Sequence is if odd, then N = ((3*$N+1)/3) and if even, then N = ( $N / 2 ). Others put logic as if $N even, return { $N / 2 } and If $N odd, return (3*$N+1). Continue the collatz_sequence until returned item is 1 or start of repetition. The speed of the supporting procs IsOdd and IsEeven were undetermined.
# formula for Collatz_Sequence
# By custom, the end of the partial collatz_sequence
# is 1 or start of repetitive integers.
# if odd, then N = ((3*$N+1)/2)
# if even, then N = ( $N / 2 )
if {$number % 2} {
# Odd ;
set number [expr {(3 * $number) + 1}]
} else {
# Even ;
set number [expr {$number / 2}]
}Modified Collatz_Sequence
The modified_Collatz_Sequence is slightly different 2nd equation ((3*$N+1)/2), used for faster and different numbers resolution as outlined in [L1 ]. The formula for modified_Collatz_Sequence produces different terms, but resolves quicker in fewer terms. The logic is if odd, then N = ((3*$N+1)/2) and if even, then N = ( $N / 2 ). The modified formula in the following code may switched in the main _Collatz_Sequence proc.
Returning to the previous example, the collatz_sequence for integer 5 is < 5 16 8 4 2 1 > Whereas the modified_collatz_sequence for integer 5 is < 5 8 4 2 1 >. The modified_collatz_sequence offers fewer terms and faster resolution.
# formula for modified_Collatz_Sequence
# produces different terms, but resolves quicker in fewer terms
# By custom, the end of the partial collatz_sequence
# is 1 or start of repetitive integers.
# if odd, then N = ((3*$N+1)/2)
# if even, then N = ( $N / 2 )
if {$number % 2} {
# Odd ;
set number [expr {((3 * $number) + 1) / 2}]
} else {
# Even ;
set number [expr {$number / 2}]Piece-wise Curve Fit to the Terminus of Collatz_Sequence
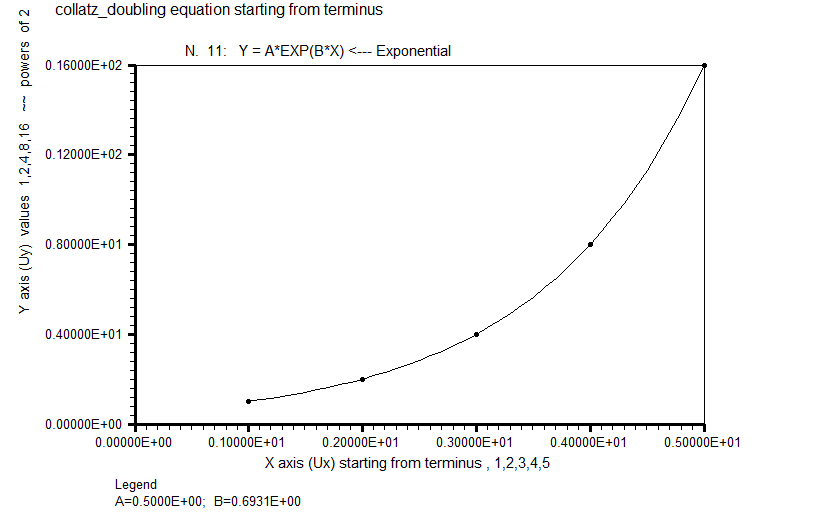
My back ground is engineering. When I am told to set a machine control system on the on the "safe part" of a complex curve, I will attempt a piece-wise curve fit on a complex curve. I look for parts of the curve that I know how to fit or understand. The start and middle of the Collatz_Sequence seems random looking, very unpredictable, and subject to initial conditions, meaning the starting integer which gives random looking results. In contrast and looking backwards from 1 at the end, the terminus of the known Collatz_Sequences is very familiar, known as the doubling equation of integer 2. The fit to the collatz_doubing equation as Y = A*EXP(B*X) Exponential.Returning to the previous example, the collatz_sequence for integer 5 is < 5 16 8 4 2 1 >. The exponential curve is matching 5/6 or 83.3 percent of the Collatz_Sequence for integer 5. Obviously, the fit will degrade with the longer Collatz_Sequence. But i think this is a start. Maybe the Collatz_Sequence is related to the doubling equation, exponentials, interest rate curves, and Gauss_Legendre correction constant. Refer to Gauss_Legendre correction constant using prime functions in TCLLIB primes::primesLowerThan [L2 ]. The accuracy of the Gauss_Legendre functions on prime number density is amazing to me, but I am not a pure mathematician.
Bottom Line. We now have exponential equation coefficients modeling the Collatz_Sequence tail as B or Beta constant 0.69314718055 (12 places) from double precision Fortran. Double precision Fortran at 12 places is roughly equivalent to TCL statement "set tclprecision 17" in the Collatz_Sequence test suite. Maybe this is overkill on precision. But the famous mathematicians Gauss and Legendre used rational numbers, exponential, and log equations to model the density of prime integer numbers on the number line. Legendre employed a corrective factor A of either 1 or approximately 1.08366 in his Gauss_Legendre formula, Prime integer number density P= N1 / (log (N1)-A). This is roughly equivalent to single precision in Fortran, although the mathematics of Gauss and Legendre predated the invention of the electronic computer and Fortran. Refer to Gauss_Legendre correction constant in the prime functions employed in TCLLIB primes::primesLowerThan [L3 ]. I agree that modeling parts of the Collatz_Sequences with exponentials and logs in rational numbers is a contrarian strategy and long shot. Frankly, my bets are on the rational number horses of Gauss and Legendre.
Exponential curve fit to reverse_Collatz_Sequence , similar to doubling equation
1 1
2 2
3 4
4 8
5 16
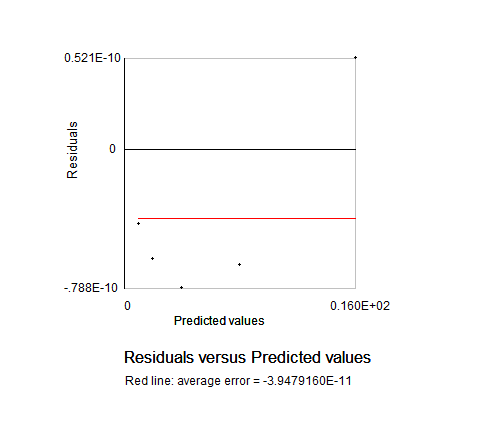
Y = A*EXP(B*X) Exponential curve fit, Levenberg_Marquadt fit to 12 places in double precision Fortran.
A = 0.50000000003E+00 SIGMAA = 0.15660160550E-10 0.319282E+11 0.000
B = 0.69314718055E+00 SIGMAB = 0.66408795386E-11 0.104376E+12 0.000
Res_av = 0.301611E-09 / 5 => Res_av = 0.603222E-10
Chi-Square:
Deg. Freed.= 3 ChiSq.=0.300001E+01 Red. ChiSq.=0.100000E+01 => P(Red. ChiSq.)=0.391
Correlation Coeficient:
R²yy(x) = 0.1000000E+01 adjR²yy(x) = 0.1000000E+01
Ryy(x) = 0.100000E+01 => P(NP,|R|) = 0.000E+00
B or Beta constant 0.69314718055 (12 places) is expr { (exp (1))**0.69314718055 } evals 1.99999999998, rounds to 2
found exact match on 5 of 6 points, expr { 5./6. * 100. } # returns 83.33 percent Gamblers_Ruin_Expectation, Probability, and Bound Limits on Collatz_Sequences
Terence Tao has published some auxiliary formulas for probability quantities etc from his Collatz_Sequences developments, which might be treated as large real precision numbers in TCL. Although Terence Tao does not use the TCL terms, as one might expect from the "pure" mathematician. The Collatz_Sequence Orbit Expectation has the form expr { (1./2.)*log(3./4.)}, which approximates Negative -0.143 from the Tao paper. Generally, the Orbit Expectation E(P(N)) is negative or a reduction over the region < 0 ... N >. But the region < 0 ... (N+1) > might be different. The Gauss_Legendre formula, Prime integer number density P(N) = N1 / (log (N1)-A) is also over the region < 0 ... N >. Maybe comparing apples and oranges, the Gauss_Legendre formula is effectively a reduction of numbers to primes on the region < 0 ... N >. The Orbit Expectation E(P(N)) is effectively a reduction of the probability envelope striking individual N's over the same region < 0 ... N >. The qualifiers in comparing other previous reports and different symbolic notation are tricky to me, but Allouche reported theta approx 0.869 and Korec reported theta approx 0.7924. Check that expr 4**(0.869**2) returns 2.848 and that expr 5**(0.869**2) returns 3.371.
An example from a wildly different subject is the Gamblers Ruin Expectation E(P(N)). The Gamblers Ruin Expectation E(P(N)) is included under the topics of Random Walks. As defined here, expectation E(P(N)) is the combined probability over 1 or more games with a constant win probability for each game. The example here is 50 percent chance of winning for each game and complement percentage for losing. The Expectation E(P(N)) or Gamblers chance of going broke after N successive games is E(P(N)) = < 0.5 + 0.25 + 0.125 + . . Nth game >. The general E(P(N) formula over the total games until finish is formula E(P(N)) = expr {1. - (1./2.)**$N} . The more games, the closer the E(P(N)) approaches 1. The Expectation E(P(N) for an infinte set of games is 1, meaning a dead loss over all total games. Check for 1 game is expr {0.5 } returns 0.5. Check for 2 games is expr {0.5 + 0.25 } returns 0.75 Check for 3 games is expr {0.5 + 0.25 + 0.125 } returns 0.875 and ''expr { 1. - (1./2.)**3. } returns 0.875. Check for 4 games is expr { 1. - (1./2.)**4. } returns 0.9375. The Gamblers Expectation of win over all games or original flush state at E(P(N)) = 0 is not expected here, but still can not be ruled out.
proc Gamblers_Ruin_Expectation {games probability_win} {
if { $games <1 } {
return -code error "The games must be 1 or larger "
}
expr {(1.-($probability_win**$games))} }
# game 1 0.5 returns 0.5
# game 2 0.5 returns 0.75
# game 3 0.5 returns 0.875
# game 4 0.5 returns 0.9375
# game 3 .14 returns 0.997256
proc collatz_sequences_Krasikov_Lagarias_limit {limit} {
if { $limit <= 1 } {
return -code error "The limit must be larger than 1"
}
expr {$limit** 0.84}
}
# Krasikov and Lagarias limit 4 3.204
# Krasikov and Lagarias limit 5 3.864
# Krasikov and Lagarias limit 10 6.918
# Krasikov and Lagarias limit 20 12.384
# Krasikov and Lagarias limit 50 26.738
set Rehder_limit_collatz_sequences [ return [ expr { (log(3)/log(2))/(log(3)/log(2)+1.)} ] ]
# returns 0.61314719276545848 or or 61.3 percent
set Rehder_limit_collatz_sequences [ return [ expr { 1.- (log(3)/log(2))/(log(3)/log(2)+1.)} ] ]
# returns 0.3868528072345415 or 38.6 percent
# Crandal developed some limits on his Collatz-like crandal_sequences,
# which are much different and shorter from Collatz_Sequences.
proc crandal_sequences_height_crandal {m } {return [expr {( log($m)) / ( log(4./3.))}]}
proc crandal_sequences_height_crandal_modified {n} {return [expr { 2.* (log( $n))/(log(16./9.))}]} Bounds and Limits on the Collatz_Sequences help define the CS. trajectory and envelope
Recent results have indicated that there are bounds and limits on the Collatz_Sequences that might be useful in TCL expressions.Motta, Oliveira, and Cataban reported that the growth between successive odds is 3/4 . Hence, the reasonable expectation or guess that the sequence will reduce in time. A rigorous result from Krasikov and Lagarias was that the number of N's that inside the region 1 to N that will coalesce or reduce to 1 is greater than expr { $N**.84} . Wulf Rehder reported that the bound on the Collatz_Sequences return to the original entry integer was a constant. The Rehder_limit_collatz_sequences constant is expr { (log(3)/log(2))/(log(3)/log(2)+1.)} returns 0.61314719276545848 or 61.3 percent. The complement or < 1 - Rehder_limit> is 0.3868528072345415 or 38.6 percent . Meaning for long Collatz_Sequences and N>20 is that if one is at the Rehder_limit or return boundary of a long Collatz_Sequence, one can estimate the length of remaining steps of the tail. The Collatz_Sequence has 38.6 percent of tail left. It is curious that some of the TCLLIB Gauss_Legendre estimates for numbers of primes less than N are hovering over the lengths or step numbers of some Collatz_Sequences, N<50. Maybe numerical coincidence, but possibly these Gauss_Legendre procs could be hacked into predicting the length of some Collatz_Sequences. These results are not complete mathematical proofs of the Collatz Conjecture, but believe that the bounds will help characterize the envelope or trajectory of the longer Collatz_Sequences.
Trial formulas and boundary limits. Lopsy posted that a number n has rough approximate ~A*log(n) Collatz steps to reach 1. Some Collatz_Sequences with 2 or more downward sequences and multiple breakpoints may be outliers to this ~A*log(n) formula. From trial calculations, it appears that A*log(n) is only useful to model in small regions and must be continually rescaled over the numberline. There are other possibilities such that Gompertz, Logistic and other S curves looked promising. Have to check out ~A*log(n) Collatz steps. There are 7 steps for integer 10 whereas numberPrimesLegendre 10 returns 7.677. There are 23 steps for integer 100 whereas numberPrimesLegendre 100 returns 27.73, a little off. The Collatz_Sequence for 10 is < 10 5 16 8 4 2 1 > with 7 elements. By inspection, the Collatz_Sequence returns or drops below 10 between elements 3 and 4 or numbers 16 and 8 in the sequence. The Rehder_limit estimates the break point as expr { 7. * .613 } returns 4.291 , rounds to 4. The approximate number of terms or computer steps is 7. Using the Rehder_limit, Rehder_complement, and the expected tail of < 16 8 4 2 1 > , the approximate number of elements is estimated as expr { ( 4.* .613 ) / .386 } returns 6.352, a little off. The Collatz_Sequence for 27 has 112 elements. Sequence for 27 has two breakpoints on elements 96 and 104. At 96, breaks between 46 and 23. The Rehder_limit estimates the break point as expr { 112. * .613 } returns 68.656 , rounds to 69. llength sequence_27_breakpoint returns 96. Sequence for 27 has 16 elements in tail.
Trial formulas and boundary limits. Crandal developed some limits on his Collatz-like crandal_sequences, which are much different and shorter from Collatz_Sequences. Crandal reported two approximate estimate fouas for the “ height” of crandal_sequences_height_crandal {m} approximate $m)) / ( log(4./3.))} and crandal_sequences_height_crandal_modified {n} approximates expr { 2.* (log( $n))/(log(16./9.)), particularly looking in the region between 1 and 10E5. The definitions and terms used here are from Crandal’s paper.
Body : Comments and Rewrite by HE
HE 2021-09-11: Hello Gold, I have a bunch of suggestions/questions about the code. Mainly in respect to other operating systems but, also if one is using your code in a win10 or related system. This is not to bother you.
As far as I understand your code is planned to be executed on a command line. There is no input. And, output is completely done by using 'puts'. It also use only commands/procedures provided by a Tcl only installation (beside some lines I will discuss below). That means the code should be possible to execute everywhere where we can call a tclsh and copy or source the code into it.
Poorly this doesn't work. Because the code contains "package require Tk" without using any GUI and some installation will not have a Tk. And using the command 'console' which is only available in wish.exe but not in wish compiled for Linux, for example.
For sure some could simply copy the code between "package require Tk" and the usage of 'console' at the end to try to get it running. That will not work because there is a 'console show' in between. This needs also to be excluded. At the end the user interested of the result of your script needs to investigate the code to get it running. A bit inconvenience from my point of view. Particularly because all the problematic lines are mainly for eye candy only.
How would I try to execute this type of scripts: On win10 I would open a wish. It displays a console window. I would make a copy and past (c&p) of the code into this console window. The output would be crude to read because of:
- all the output before "proc table_format_out ..." would not be easy to read because the 'puts' lines and the output are interchanging.
- The change of font and geometry left a console window far to big on some displays and not able to show the text in a readable way. At least not for me.
- I don't discuss the format of the able output here, because this also not help to read the results.
Next try would be to open a tclsh on win10 and c&p the code into it. The result is similar. The font size and console background can't be changed so it is more comfortable to read. But the other issues mentioned above still exists and in addition we have the error message in between about the 'console' command.
Next try would be to store it in a file, start a tclsh on win10 (because "package require Tk" let me think it is planned to do so) and source the file into it. This simply raise a "Invalid command name "console"". This will be the same on Linux.
Next try would be to start a wish on win10 and source the stored file into it. I think that is the result you wanted. But, eye candy for you on your computer doesn't fit well on my computer. You also don't know if the user will have problems with a green background. And a smaller font size would show more from the table. At least on the computer I tried your code.
Now I tried all four variants on Linux. Sourcing the file lead in both cases to error message "invalid command name "console"" without any other output. C&p into a wish or tclsh lead to the ugly output where it is not clear where to look for the wanted result.
What I would change:
- To be platform independent I would remove "package require Tk" and the 'console' lines.
- To be able to run it by double-click inside win10 I would add somewhere at the top of the script:
if {$tcl_platform(platform) == {windows}} {
console show
}- I would put all output into one procedure so that the last command could this procedure and afterwards all output is generated.
Sorry again, for all the comments only because of output and executing. I tend to write to much in case I try to explain my view. But look how easy it is to make the code run in 8 different conditions instead only running under one condition.
Until here, I read so often this piece of code that I found some small other items:
- Procedures isPositive and isNegative are not used. Perhaps, isPositive was planned to be used in collatz_sequence as a protection not to use negative numbers?
- "set tclprecision 17" is used. The Tcl 8.6 documentation tells "It defaults to 0. Applications should not change this value;". I'm not sure to understand why it is used. The whole math of that problem should be integer calculation. At least until the limit of 8 byte integer is crossed. And as long as no fraction is forced the math should stay integer. Perhaps, I'm wrong. But, that is I understood how Tcl calculation works.
- Where you are using the math packages you load in the beginning? I can't find the usage of it. I would understand "package require math::bignum" to be able to calculate behind the 8 byte integer limit. But the named one?
HE 2021-09-12: Since my comment yesterday, all comment lines are changed from '#' to ';#' at the beginning. Is there a reason for this? From my knowledge a ';' is not need for a proper comment at the beginning of a line. Only if the comment is behind a command on the same line a ';' is needed before the '#' to separate both commands.
HE 2021-09-12: As an answer of your question on Ask, and it shall be given # 13 here my version of collatz_sequence based on your one.
- For loop provide everything to control iteration.
- Some tests in the beginning to assure that positive integers are used for number and iteration.
That makes it easier to stop as we find 1 as a result. At least the first 10 million integer I tried to use for number will all end with 1 and then go to the endless sequence. As far as I understood others are tried far higher numbers with the same end. Also I would not check separately for odd and even. One check is enough. And I used the expression itself instead of put it into a separate procedure. This will spare calculation power with bigger numbers.
Easy Eye Concept for Windows10 Console
The easy eye calculator includes large black font on green background. The human eye is peaked for yellow/green and various ergonomic studies have shown that black font on green background is one of the easiest to read. The easy eye concept is similar to the more legible screens in the older monochrome green screens and monochrome yellow screens, as well as the old MS-DOS texteditor program Wordstar. Used in military green screens, also. My small notepad has a linked script and icon for easy eye calculator, posted on the windows desktop of small screen, 22 by 12 cm. One advantage of the easy eye calculator is that the calculations are posted to a console window as a sort of paper tape. The easy eye calculations can be cut and paste, saved to a word processor. The easy eye calculator is a compilation of several eval calculators on the TCL wiki.
gold However, HE suggestion for Windows10 Console programs allowing user preference for screen background and choose fonts is good. One can change the color and fonts right now through the top boxes on the Windows10 console. Probably one would need to access a storage file for saving preferences. Have to think on this. Not everybody has my bad eyes, so tired from 50 years of tiny computer fonts.
Test Suite
The test suite for Collatz_Sequences has been completed and forwarded attached to ticket e035b93f36. However, the Collatz_Sequences test suite has many dependencies on the Windows10 PC and the ActiveState TCL Comsole window. At present, all i do is tap once on the icon on the Windows PC; the icon text is linked to ActiceState TCL. And I am up and running on test suite gui for Collatz_Sequences. I am not sure how one could test a numeric program without some listing of canned test cases, printout, or other wiki style printout? I might point that to test compatibility with TCLLIB, I do test homebrew code loaded in the local copy of TCLLIB math and associated libraries. This is a local setup on Windows10 PC and ActiceState TCL libraries, so references in code here to a my local TCLLIB::math library and the ( ActiveState ) TCL Comsole window might not be easily portable, based on UNIX comments received here. I suppose that the Collatz_Sequences test suite could be compiled to a Windows10 executable. But then the testing and issues on UNIX machines still remain unclear at present.
Pushbutton Operation
Alternate Draft text from test suite. 1) initial integer N1 2) iteration limit $iteration 3) optional index for heads and tails, usually 4 4) optional mode constant 1 or 2, calc reverts to number of calc steps This calculator returns the partial Collatz_Sequence based on initial integer and iteration number of steps optional constant mode, usually 1 for no decay, not used & open yet, optional constant iteration is safety break for brevity and counter endless loops iteration maybe cut short for brevity The collatz_sequence proc returns the partial collatz_sequence from positive integers. This collatz_sequence proc can easily generate an endless loop. In fact, the known collatz_sequences are an endless list or coalesce to 1 or a repetitive string of integers. The iteration number is a stop or limit steps of iteration. By custom, the end of the partial collatz_sequence is 1 or start of repetition integers max_values_list is short list of maximum values in list, number of maximum values controlled by an index number collatz_sequence_head is initial values at start of sequence collatz_sequence_tail is initial values at end of sequence optional mode constant 1 or 2, calc reverts to number of calculation steps: mode_option 1 is collatz_sequence mode_option 2 is modified_collatz_sequence if mode 2 used, best to clear and recycle with another testcase collatz_sequence_length is maximum length of partial collatz sequences warning!!! if index & iteration activated for brevity, sequence list maybe cut short collatz_sequence is list of collatz_sequence warning!!! if index & iteration activated for brevity, sequence list maybe cut short steps_iteration_total is total number of steps used in calc proc For comparison, TCL code may include redundant paths & formulas. The TCL calculator normally uses modern units for convenience to modern users and textbooks. Any convenient and consistent in/output units might be used like inches, feet, nindas, cubits, or dollars to donuts. Recommended procedure is push testcase and fill frame, change first three entries etc, push solve, and then push report. Report allows copy and paste from console to conventional texteditor. For testcases testcase number is internal to the calculator and will not be printed until the report button is pushed for the current result numbers. Use one line errorx proc to estimate percent errors. errorx proc is used in the report window (console). Additional significant figures are used to check the TCL program, not to infer the accuracy of inputs and product reports. index is number of sequence values displayed from start of sequence warning!!! if index & iteration activated for brevity, sequence list maybe cut short, including integers, maximum values, heads and tails reported comments are placed outside these working routines because comments are deleted in final TCLLIB version, I think.
For the push buttons on the TCL calculator, the recommended procedure is push testcase and fill frame, change first three entries etc, push solve, and then push report. Report allows copy and paste from console. For testcases in a computer session, the TCL calculator increments a new testcase number internally, eg. TC(1), TC(2) , TC(3) , TC(N). The testcase number is internal to the calculator and will not be printed until the report button is pushed for the current result numbers. The current result numbers will be cleared either on the next clear button or on the next solve button.
Insights into the Collatz Infinite Sequences
Clipping off the repeating terminus of the known Collatz Sequences means the sequence is still fundamentally an infinite sequence. However, the mathematicians have changed some of the original formula to make the Collatz sequence close faster. The modified Collatz sequence does close faster and has a smaller envelope with the term (3*N+1)/2. As an analogy, this is similar to the converging and diverging of a series. The original Collatz sequence is a divergent sequence in that sense, because the Collatz sequence never closes to an exact numerical limit. Briefly, similar terms to Collatz sequences are possible as generic ($C1 * N + $C2)/2. Another breakdown in similar terms to Collatz sequences is (N+2*N+1)/2. The advantage of (4*N-1*N+1)/2 is that a fourth math operation {+-*/} is added to in the original setup {+*/}. Since I have worked more with converging series on this wiki etc, I would be interested in turning the Collatz sequences into a converging series. Possibly a Collatz sequence morfed into successive ratios like the successive Fibonacci series produce the Golden Ratio (1.618) . From the previous examples, the collatz_sequence of 5 is < 5 16 8 4 2 1 >. Converts to < 8/16 4/8 2/4 1/2 > and sum from expr { 8/16. + 4/8.+ 2/4.+ 1/2. } , 2. Possibly, sum is number of terms times half?, $ND*(1./2).
Possible Uses of Collatz Sequences Conjecture
Offsite query from Senior TCL Enginner. 9/22/2021 was "What are the possible computer application uses of the Collatz Sequences Conjecture?
As understood here, the Collatz Sequences Conjecture is called pure mathematics. Paul Erdos said about the Collatz conjecture: “Mathematics may not be ready for such problems.” The Collatz Sequences Conjecture is at the forefront of human mathematics. The topic of the Collatz Conjecture was rated "High Priority" by WikiProject Mathematics circa Sep2021, a collective measure of Mathematicians priorities and popularity to be sure. From what an outsider can tell, the Collatz Sequences are being generated with supercomputers and distributed computing algorithms on the numeric issues. Apparently, the Collatz Sequences are as valid a test for computing machines, parallel algorithms, and distributed computing algorithms as the 1) search for pi, 2) search for highest prime number, 3) Twin Prime Conjecture, and 4) factoring numbers. In 2020, starting values up to 2**268 approximating 2.95*1020 have been checked in the Collatz conjecture. In 2019, a paper proposed using Collatz Sequences for signal encryption, High-uncertainty audio signal encryption based on the Collatz conjecture. Other papers have mentioned the buzzwords "quantum mechanics computing" and fuzzily implied that the Collatz conjecture may be analogous to setting quantum levels in a quantum device. I am a retired engineer. I have put some queries out to the pure mathematicians.
Alan Turing created the concept of a “universal computing machine” about 1937. The seminal 1937 paper was titled: On Computable Numbers With an Application to the Entscheidungsproblem. A Turing machine is a theoretical abstraction of a computing engine, but usually is presented and resolved to a computer program on existing physical computers today. There have been a number of papers laying out concepts for Turing machines based on the Collatz Sequences Conjecture. These Turing machine concepts usually use the Collatz Sequence calculations and procedures <+,/,*> in a decision matrix and rate how the conceptual Turing machine smoothly solves for Collatz Sequences in a continuous computation loop without halts and flaws. I might point out that the original Collatz Conjecture procedures involving simple <+,/,*> operations here have been spun out into Collatz-like problems, different formula approaches, and radical looking reformulations.
gold 9/24/2021. Provisional text. I still have some queries out to pure mathematician associations and institutions on Collatz Sequences uses. If they answer queries, the pure mathematicians may come back with different and more authoritative uses of Collatz Sequences than the retiree brigade.
It is fascinating to witness the diverse applications of mathematical concepts like the Collatz Sequences Conjecture in various fields, including computer science and engineering. The potential uses of the Collatz Sequences Conjecture in signal encryption and quantum mechanics computing demonstrate the far-reaching impact of these mathematical theories on the development of new technologies. The exploration of Turing machine concepts based on the Collatz Sequences Conjecture highlights the ongoing efforts to understand the limitations and capabilities of computing systems. These mathematical theories can be applied to improve communication technologies and systems. It is also intriguing to see how the Collatz Sequences Conjecture has inspired new mathematical problems and reformulations, leading to a deeper understanding of the underlying principles of these theories. These developments will continue to shape the course of scientific discovery and technological progress in the years to come.
Gist and Outline on the applications on the Collatz Sequences
The Collatz Sequence, also known as the 3n + 1 problem, is a mathematical sequence that starts with a positive integer n and follows a specific rule: if n is even, divide it by 2; if n is odd, multiply it by 3 and add 1. The sequence continues until it reaches the number 1. The Collatz Sequences serve as a fascinating and versatile mathematical concept with applications in various fields of study. Its simplicity and complexity make it a valuable tool for exploring mathematical patterns and phenomena. The Collatz Sequence has several applications and implications in mathematics and computer science:
1. Mathematical research and Number Theory: The Collatz Conjecture, which states that the sequence will always reach the number 1 regardless of the starting integer, remains an unsolved problem in mathematics. Collatz sequences have been a subject of interest in number theory and combinatorics. Researchers study the behavior of these sequences, trying to determine if they always reach 1 for any given starting number, or if there are any patterns or properties that can be derived from them. Studying the properties of the Collatz Sequence can lead to insights into number theory and the behavior of integers.
2. Algorithm Analysis: Collatz sequences are a popular example of a simple algorithm that can be implemented on a computer to demonstrate the power and limitations of computational methods. The Collatz Sequence is often used as a benchmark for testing algorithms and computational methods. Analyzing the sequence can help researchers understand the efficiency and complexity of different algorithms.
3. Cryptography: The Collatz Sequence has been used in certain cryptographic algorithms and protocols. The unpredictable nature of these Collatz sequences can be exploited to create secure encryption schemes, random number generators, and hash functions. The iterative properties of the Collatz sequence make it a potential candidate for generating random sequences or cryptographic keys. There are nebulous comments that the Collatz sequence forms have been considered for backing Bitcoin or other digital currency.
4. Chaos Theory: The Collatz Sequence exhibits chaotic behavior, with seemingly random fluctuations and patterns. Studying the dynamics of the sequence can provide insights into chaos theory and nonlinear systems. There has been major breakthroughs on Collatz studies in base 3 and unusual bases, ref papers of Idriss J. Aberkane.
5. Artificial Intelligence: Collatz sequences can be used in the development of artificial intelligence algorithms. For example, researchers have used them to study the behavior of neural networks and to develop algorithms for solving complex problems.
6. Educational Purposes: The Collatz Sequences are often used as a teaching tool in mathematics and computer science courses. Collatz sequences are a great tool for teaching basic concepts in mathematics and computer science. Collatz sequences can be used to introduce students to algorithms, recursion, and problem-solving techniques. Collatz sequences can help students understand recursion, iteration, and the concept of proof by induction.
Conclusions
gold Many thanks to HE for comments and feedback. In terms of use on other TCL platforms, I am interested in proving and petitioning the collatz_sequence code to the TCLLIB. On my own PC on Windows 10, mostly I attach a proven subroutine to the command line interface and type into the TCL Windows10 console, meaning Easy Eye [L4 ]. At present, all i do is tap once on the icon (text linked to ActiceTCL) of the Easy Eye console and I am up and running. I am not sure how one could test a numeric program without some listing of canned test cases, printout, or other wiki style printout? I might point that to test compatibility with TCLLIB, I do test homebrew code loaded in the local copy of TCLLIB math and associated libraries.This is a local setup on Windows10, so references to a my local TCLLIB::math library would not be portable.
gold 2021-09-13. "And slowly, I turn inch by inch" - Movies. I have swapped ;# for # in comment lines. I have seen punctuation ;# semicolon hash and set list_values { 1 2 3 4 } before as a list creation, meaning from some professional coders on the internet. But I will defer to your judgement here. In 2020, starting values up to 2**268 approximating 2.95*1020 have been checked in the Collatz conjecture. Yes, one would need math::bignum and math::bigfloat package for that and to check all speed savings on supporting integer procs for Collatz sequences at that size. Recognize that collatz_sequence are considered integer sequences, but Gauss and Legendre used exponential and logs on real numbers to predict the Prime integer number density on the numberline. Terence Tao has published some auxiliary formulas for probability quantities etc from his Collatz_Sequences developments, which might be treated as large real precision numbers in TCL. Although Terence Tao does not use the TCL terms of real decimal numbers, as one might expect from the "pure" mathematician. I am loading my exponential cannon with real numbers and TCL gunpowder, set tclprecision 17. Refer to Gauss Approximate Number of Primes and eTCL demo example calculator. According to Richard Suchenwirth on TCL wiki, and quoting directly " Since the console is a TK text widget, you can use all text widget commands and options on it." Refer to [L5 ] The grid Tk widget, grid Tk widget, and Tk::button all support the panel display of the Windows10 gui here. I am still learning TCL/TK. And I can not rule out that dropping the statement "package require Tk" in the Windows10 decks might have unforeseen consequences, to include other user Windows10 machines if not my own Windows10 setup. The title of wiki page and original TCL program included words '"Console Example" and "written on Winidows10". I think that the TCL WIKI is big enough to support both UNIX and Windows10 in separate groups, modus vivendi. However, your good comments have catalyzed me. I will start looking for a graphical user interface gui or template code that is cross platform, equally accessible to UNIX and Windows10. Aside from Windows10, and TCL, I wrote about 20 years of calculator guis on Javascript and UNIX at work. The main task for me was getting the Tcllib ticket on Collatz_Sequences out the door.
gold 2021-09-21. I have the TCL gui graphical user interface for Collatz_Sequences working on Windows10 Console TK widget in under 288 lines of code. Meaning, one tap on the icon of the ActiveState TCL Console gets one up and running on Windows10. The gui dependency on the ActiveState TCL and Windows10 Console Tk widget has been noted sufficiently on the page title and source code. Respectfully, I remind one that I have been out of the classroom for 50+ years, and Fortran77 classes at that. I hope I may be forgiven for a few UNIX faux pas in a Window10 Console program. I welcome others on the Wiki to proof, improve, or proof the code on UNIX machines on any independent UNIX pages. I believe that the proposed implementation of the Collatz_Sequences functions in the Tcllib will accommodate the UNIX users of TCL. Sep2021 PM quote, "ActiveTcl users are overwhelmingly on Windows (80% or so), and tend to have a high proportion of novice to intermediate users." One may infer that the UNIX users of ActiveState TCL are a very intelligent, more experienced Linux users, and very sophisticated set of TCL users, if not driving the pack. I do not have all the answers. Maybe, as one infers, the ActiveState TCL Windows10 Console and TK widgets are not the best path?
gold 2021-09-13. Solved problem. The proc collatz_sequence was substantially rewritten by HE and I replaced in the main deck and good feedback comments, which I will have to chew on. Many thanks to HE. I checked the proc collatz_sequence in small test suite and proc looks good, so I will pass ticket on to TCLLIB math. I have loaded the ticket e035b93f36 Title: Collatz_Sequence, modified_Collatz_Sequence, positive & negative logic test for integers.
gold 2021-09-13. These calculator approaches in TCL console guis for Windows10 may seem trivial math to some, but I have submitted 4 or 5 TCLLIB tickets to improve the TCLLIB math library. For example, the math and logic functions IsOdd, IsEven, IsNegative, IsPositive, figurative_numbers, and Quadratic_Equation_Solution_for_reals were not in the TCLLIB library, as near as I can tell. Maybe these logic functions on integers and Quadratic_Equations_Solutions on reals are trivial math to some, but these Quadratic_Equations_Solutions and other math functions show up in some other math languages, TCL programs, and even TCL WIKI pages. As HE implies, the main idea of TCL or other computer language is that other users can share the faster compiled code rather than homebrew functions. Since I am retired and I do not have easy access to a UNIX machine, the only course in the retirement economy is to proof the TCL routines on a Windows10 PC.
References:
- A popular introduction to the Collatz and Furstenberg conjectures
- Keynote at Huelva University
- Idriss J. Aberkane
- Collatz Attractors Are Space-Filling
- by Idriss J. Aberkane
- An Algorithm for Linearizing the Collatz Convergence
- by Alexander Rahn, Idriss J. Aberkane, etc
- Wikipedia search engine < Collatz Sequences >
- Wikipedia search engine < Lothar Collatz Sequences >
- Wikipedia search engine < Programming Examples >
- Google search engine < vaporware >
- Google search engine < Collatz_Sequences >
- Book >> How to Prove The Collatz Conjecture Paperback, 2005, by Danny Fleming
- Ultimate Challenge: the 3x + 1 problem: edited by Jeffrey Lagarias,
- One Liners Programs Pie in the Sky
- One Liners
- Playing Recursion V2 >> demo examples for one liner programs
- One Liners Programs Compendium [L6 ]
- WIKI BOOKS, Programming_Examples pdf
- WIKI BOOKS, Tcl_Programming_Introduction pdf
- google search engine < Collatz Conjecture >
- switch
- Tcl Tutorial Lesson 6
- Math Sugar Richard Suchenwirth RS
- Practical_Advice_on_Quotes_and_Brackets_in_TCL
- tmml.sourceforge.net/doc/tcllib [L7 ]
- rosettacode.org/wiki/Even_or_odd [L8 ]
- en.wikipedia.org/wiki/Collatz_conjecture
- Tao, Terence , 2019. "Almost all Collatz orbits attain almost bounded values".
- Project Euler 14: Longest Collatz sequence, Peter Prevos
- Mathematician Proves Huge Result on ‘Dangerous’ refer to Terence Tao
- Terence Tao realized that the Collatz conjecture was similar to partial differential equations.
- The Tao starting sample weighs toward numbers that
- have a remainder of 1 after being divided by 3,
- and away from numbers that have a remainder of 2 after being divided by 3.
- TCL pseudocode
- remove all numbers divisible by 3 on a list of integers,
- find all numbers that have a remainder of 1, when divided by 3.
- see modified Collatz formula in en.wikipedia.org/wiki/Collatz_conjecture
- Barina, David (2020). "Convergence verification of the Collatz problem". The Journal of Supercomputing.
- Random Walk Equation Slot Calculator Example
- oeis.org/A070165, abbreviation for "The On-Line Encyclopedia of Integer Sequences"
- docs.google.com/spreadsheets/d/1TB5FpgjsYVAyuqQKu4WDrmB5u7UDUY5KaQZfjqPNr9I/edit#gid=0
- Collatz Conjecture: Spreadsheet 2021,
- Project: Spreadsheet Based Modelling for Education and Research
- Amro Mohamed Elfeki, Mansoura University
- rosettacode.org/wiki/Rosetta_Code
- rosettacode.org/wiki/Hailstone_sequence, not sure of permissions and usage
- But I suppose these Rosetta_code functions would be useful in Collatz Sequences, proposed library in TCLLIB.
- (Awaiting Moderator Approval) Add Collatz_Sequences and modified Collatz_Sequences to ticket e035b93f36
- Ticket completed. Gauss / Legendre functions for number of primes in TCLLIB
- Ticket completed, Request for math::number_theory.
- would be handy to have 3 prime number functions like approx_number_primes = N1 / ln (N1),
- legendre_primes2 = N1 / (ln (N1)-1),modified_legendre_primes3 = N1 / (ln (N1)-1.08366).
- (Awaiting Moderator Approval) New ticket 5af6381a8b Quadratic Equation Solution, 2 reals from Muller's method.
- New ticket f8adb7a036 figurate numbers and sums of powers.
- Ticket completed, prime gap function and sets of twin primes,cousin primes,twin primes
- Krasikov, Ilia; Lagarias, Jeffrey C. Bounds for the $3x+1$ problem using difference inequalities.
- Acta Arith. 109 (2003), no. 3, 237–258.
- Wulf Rehder, from post. Rephrase the Collatz Conjecture, 29 Aug 2021, mentioned Rehder_limit constant
- Wulf Rehder, from post. Calculating the Total Stopping Time N(T):,31 Aug 2021, looks very useful
- paper. ALMOST ALL ORBITS OF THE COLLATZ MAP ATTAIN ALMOST BOUNDED VALUES, TERENCE TAO
- Terence Tao and Wolf Rehder and Tao on blog wordpress.com, try google search <wordpress Tao Rehder blog >
- wordpress.com, try google search <wordpress Tao Rehder blog >
- wordpress.com, Many articles and posts on TCL computer language. Looked high quality from preliminary searches.
- wordpress.com, try google search <wordpress TCL Tool Control Language >
- ALMOST ALL ORBITS OF THE COLLATZ MAP ATTAIN ALMOST BOUNDED VALUES, by TERENCE TAO
References on Turing machines:
- The Man Who Loved Only Numbers:
- The Story of Paul Erdos and the Search for Mathematical Truth
- 1999 by Paul Hoffman
- The Collatz Conjecture and the Quantum Mechanical Harmonic Oscillator
- Carlos Castro Perelman
- On Computable Numbers With an Application to the Entscheidungsproblem, Alan TUring, 1937
- Superb Post on Turing machines, Hector Zenil , Senior Researcher, Oxford, Lab Leader, Karolinska Institute
- Mathematical Foundation of Computers and Programs by Theo Verelst.
- Turing machine, Page originally by Lars H
- Finite state machines
- A little Deterministic Turing Machine. Richard Suchenwirth, 2005-05-03:
- A lambda calculus interpreter with arithmetic NEM 10 Sept 2006 (updated 2008-06-24):
- Small Turing machines and generalized busy beaver competition by P. Michel (2004),
- features Collatz-like problems between decidable TMs,
- where the halting problem is decidable, and Universal TMs.
- The complexity of small universal Turing machines: a survey" by D. Woods and T. Neary, 2007.
- On the boundaries of solvability and unsolvability in tag systems.
- Theoretical and Experimental Results" by L. De Mol ,2009.
- Hofstadter's MIU game
- An Automated Approach to the Collatz Conjecture by Emre Yolcu, Scott Aaronson, Marijn J.H. Heule
- Reverse engineering Turing Machines and insights into the Collatz conjecture. by John Harold Nixon, 2021
- article. www.quantamagazine.org/computer-scientists-attempt-to-corner-the-collatz-conjecture-20200826
- article. Methods for understanding Turing machine computations, 2013, by John Harold Nixon
- Quanta article. How Ancient War Trickery Is Alive in Math Today, September 14, 2021
proposed Collatz_Sequences and modified Collatz_Sequences functions in TCLLIB.
collatz_sequence_head (27, 4 ) evals 27 82 41 124 collatz_sequence_head (27, 3 ) evals 27 82 41 collatz_sequence_head (27, 2 ) evals 27 82 collatz_sequence_head (27, 1 ) evals 27 , initial entry collatz_sequence_head (10, 3 ) evals 5 16 8 collatz_sequence_tail (27, 4 ) evals 8 4 2 1 collatz_sequence_tail (27, 3 ) evals 4 2 1 collatz_sequence_tail (27, 2 ) evals 2 1 collatz_sequence_tail (27 , 1 ) evals 1, final entry collatz_sequence_tail (10 , 3 ) evals 4 2 1 collatz_sequence_tail (27, 4 ) evals 8 4 2 1 collatz_sequence_max_sequence_value (27) evals 9232? collatz_sequence_max_sequence_value (10) evals 6 collatz_sequence_length (10) evals 6 collatz_sequence_length (27) evals 111? collatz_sequence_generate (5) evals 5 16 8 4 2 1 collatz_sequence_generate (27) evals 27 82 41 124 62 31 94 47 142 71 214 107 322 161 484 242 121 364 182 91 274 137 412 206 103 310 155 466 233 700 350 175 526 263 790 395 1186 593 1780 890 445 1336 668 334 167 502 251 754 377 1132 566 283 850 425 1276 638 319 958 479 1438 719 2158 1079 3238 1619 4858 2429 7288 3644 1822 911 2734 1367 4102 2051 6154 3077 9232 4616 2308 1154 577 1732 866 433 1300 650 325 976 488 244 122 61 184 92 46 23 70 35 106 53 160 80 40 20 10 5 16 8 4 2 1 reverse_collatz_sequence_generate (5) 1 2 4 8 16 5 reverse_collatz_sequence_generate (7) 1 2 4 8 16 5 10 20 40 13 26 52 17 34 11 22 7 reverse_collatz_sequence_generate (10) 1 2 4 8 16 5 10 reverse_collatz_sequence_generate (27) 1 2 4 8 16 5 10 20 40 80 160 53 106 35 70 23 46 92 184 61 122 244 488 976 325 650 1300 433 866 1732 577 1154 2308 4616 9232 3077 6154 2051 4102 1367 2734 911 1822 3644 7288 2429 4858 1619 3238 1079 2158 719 1438 479 958 319 638 1276 425 850 283 566 1132 377 754 251 502 167 334 668 1336 445 890 1780 593 1186 395 790 263 526 175 350 700 233 466 155 310 103 206 412 137 274 91 182 364 121 242 484 161 322 107 214 71 142 47 94 31 62 124 41 82 27 # using index number in second position # Many known collatz_sequences coalesce to 1 to similiar tail, 16 8 4 2 1 # so may have to index to 8 or 9 to show any differences in reverse_collatz_sequence(N) reverse_collatz_sequence_head (10 3) 1 2 4 reverse_collatz_sequence_head (5 4) 1 2 4 8 # reporting number of computation steps for collatz_sequence(N) , would also be useful collatz_sequence_steps (27) returns 112? collatz_sequence_steps (10) returns 6? collatz_sequence_steps (50) returns 21? # collatz_sequence sorted from maximum to minimum value collatz_sequence_maximum_values (5) returns 16 8 5 4 2 1 collatz_sequence_maximum_values_short_list (10 3) returns 16 8 10?
Screenshots Section
figure 1a. Screenshot, Collatz_Sequences_(3*N+1) _screenshot
figure 1b. Screenshot, Collatz_Sequences_screenshot_gui
figure 2. Collatz_Sequences_double_collatz
figure 3. [Collatz_Sequences_residuals
figure 4. Collatz_Sequences (3*N+1) Collatz cone side view , credit Idriss J. Aberkane
figure 5. Collatz_Sequences (3*N+1) Collatz cone top view , credit Idriss J. Aberkane
Testcases Section
In planning any software, it is advisable to gather a number of testcases to check the results of the program. ---
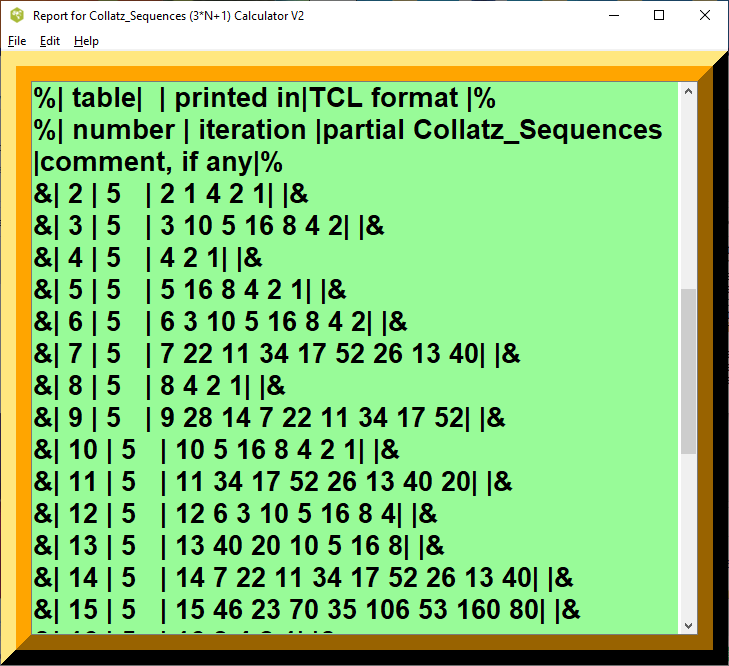
Testcase 1, Partial Collatz_Sequences
| table, Partial Collatz_Sequences | printed in | TCL format | |
|---|---|---|---|
| number | iteration | partial Collatz_Sequences | comment, if any |
| 3 | 5 | 3 10 5 16 8 4 2 1 | |
| 4 | 5 | 4 2 1 | |
| 5 | 5 | 5 16 8 4 2 1 | |
| 6 | 5 | 6 3 10 5 16 8 4 2 | |
| 7 | 5 | 7 22 11 34 17 52 26 13 40 | |
| 8 | 5 | 8 4 2 1 | |
| 9 | 5 | 9 28 14 7 22 11 34 17 52 | |
| 10 | 5 | 10 5 16 8 4 2 1 | |
| 11 | 5 | 11 34 17 52 26 13 40 20 | |
| 12 | 5 | 12 6 3 10 5 16 8 4 | |
| 13 | 5 | 13 40 20 10 5 16 8 | |
| 14 | 5 | 14 7 22 11 34 17 52 26 13 40 | |
| 15 | 5 | 15 46 23 70 35 106 53 160 80 | |
| 16 | 5 | 16 8 4 2 1 | |
| 17 | 5 | 17 52 26 13 40 20 10 | |
| 18 | 5 | 18 9 28 14 7 22 11 34 17 52 | |
| 19 | 5 | 19 58 29 88 44 22 11 34 | |
| 20 | 5 | 20 10 5 16 8 4 2 |
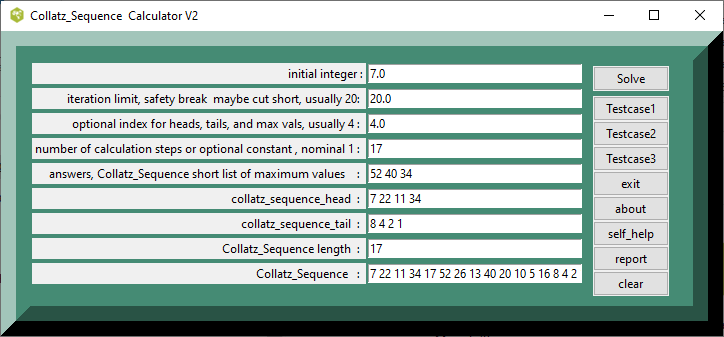
Testcase 2, Collatz_Sequence for integer 7 from Windows10 gui
| table 2, Collatz_Sequence for integer 7 from Windows10 gui | printed in tcl wiki format | ||
|---|---|---|---|
| quantity | value | value | comment, if any |
| 1: | testcase_number | ||
| 7.0 : | initial integer | ||
| 20.0 : | iteration limit , safety maybe cut short : | ||
| 4.0 : | optional index_tails for heads, max values, and tails, usually 4 : | ||
| 17 : | number of calculation steps or optional constant , nominal 1 : | ||
| 17 : | steps_iteration_total: | ||
| 52 34 26 : | collatz_sequence short list of maximum values : | ||
| 7 22 11 34 17 : | collatz_sequence_head : | ||
| 16 8 4 2 1 : | collatz_sequence_tail : | ||
| 17 : | collatz_sequence_length: | ||
| 7 22 11 34 17 52 26 13 40 20 10 5 16 8 4 2 1 : | Collatz_Sequence values : | ||
| Collatz_Sequence : | 7 22 11 34 17 52 26 13 40 20 10 5 16 8 4 2 1 |
Testcase , Collatz_Sequence for integer 27 from Windows10 gui
| table 2 :Collatz_Sequence for integer 27 | printed in tcl wiki format | ||
|---|---|---|---|
| quantity | value | value | comment, if any |
| 2: | testcase_number | ||
| 27.0 : | initial integer | ||
| 200.0 : | iteration limit , safety maybe cut short : | ||
| 4.0 : | optional index_tails for heads, max values, and tails, usually 4 : | ||
| 112 : | optional constant , nominal 1, calc reverts to number of calc steps : | ||
| 112 : | steps_iteration_total: | ||
| 9232 : | collatz_sequence short list of maximum values : | ||
| 27 82 41 124 : | collatz_sequence_head : | ||
| 8 4 2 1 : | collatz_sequence_tail : | ||
| 112 : | collatz_sequence_length: | ||
| 1 2 4 8 : | reverse_Collatz_Sequence head : | ||
| 1 2 4 8 16 5 10 20 40 80 160 53 106 35 70 23 46 92 184 61 122 244 488 976 325 650 1300 433 866 1732 577 1154 2308 4616 9232 3077 6154 2051 4102 1367 2734 911 1822 3644 7288 2429 4858 1619 3238 1079 2158 719 1438 479 958 319 638 1276 425 850 283 566 1132 377 754 251 502 167 334 668 1336 445 890 1780 593 1186 395 790 263 526 175 350 700 233 466 155 310 103 206 412 137 274 91 182 364 121 242 484 161 322 107 214 71 142 47 94 31 62 124 41 82 27 : | reverse_Collatz_Sequence values : | ||
| 27 82 41 124 62 31 94 47 142 71 214 107 322 161 484 242 121 364 182 91 274 137 412 206 103 310 155 466 233 700 350 175 526 263 790 395 1186 593 1780 890 445 1336 668 334 167 502 251 754 377 1132 566 283 850 425 1276 638 319 958 479 1438 719 2158 1079 3238 1619 4858 2429 7288 3644 1822 911 2734 1367 4102 2051 6154 3077 9232 4616 2308 1154 577 1732 866 433 1300 650 325 976 488 244 122 61 184 92 46 23 70 35 106 53 160 80 40 20 10 5 16 8 4 2 1 : | Collatz_Sequence values : |
Testcase , Collatz_Sequence for integer 10 from Windows10 gui
| table 2, Collatz_Sequence for integer 7 from Windows10 gui | printed in tcl wiki format | ||
|---|---|---|---|
| quantity | value | value | comment, if any |
| 2: | testcase_number | ||
| 10.0 : | initial integer | ||
| 100.0 : | iteration limit , safety maybe cut short : | ||
| 4.0 : | optional index_tails for heads, max values, and tails, usually 4 : | ||
| 6 : | optional constant , nominal 1, calc reverts to number of calc steps : | ||
| 6 : | steps_iteration_total: | ||
| 10 : | collatz_sequence short list of maximum values : | ||
| 10 5 8 4 : | collatz_sequence_head : | ||
| 8 4 2 1 : | collatz_sequence_tail : | ||
| 6 : | collatz_sequence_length: | ||
| 10 5 8 4 2 1 : | Collatz_Sequence values : | ||
| Collatz_Sequence : | 10 5 8 4 2 1 |
Testcase , Collatz_Sequence for integer 7 from Windows10 gui
| table 3, Collatz_Sequence for integer 7 from Windows10 gui | printed in tcl wiki format | ||
|---|---|---|---|
| quantity | value | value | comment, if any |
| 3: | testcase_number | ||
| 7.0 : | initial integer | ||
| 100.0 : | iteration limit , safety maybe cut short : | ||
| 4.0 : | optional index_tails for heads, max values, and tails, usually 4 : | ||
| 12 : | optional constant , nominal 1, calc reverts to number of calc steps : | ||
| 12 : | steps_iteration_total: | ||
| 26 : | collatz_sequence short list of maximum values : | ||
| 7 11 17 26 : | collatz_sequence_head : | ||
| 8 4 2 1 : | collatz_sequence_tail : | ||
| 12 : | collatz_sequence_length: | ||
| 7 11 17 26 13 20 10 5 8 4 2 1 : | Collatz_Sequence values : | ||
| Collatz_Sequence : | 7 11 17 26 13 20 10 5 8 4 2 1 |
Testcase , modified__Sequence for integer 10 from Windows10 gui
| table 2 modified_Collatz_Sequence | printed in tcl wiki format | ||
|---|---|---|---|
| quantity | value | value | comment, if any |
| 2: | testcase_number | ||
| 10.0 : | initial integer | ||
| 100.0 : | iteration limit , safety maybe cut short : | ||
| 4.0 : | optional index_tails for heads, max values, and tails, usually 4 : | ||
| 6 : | optional constant , nominal 1, calc reverts to number of calc steps : | ||
| 6 : | steps_iteration_total: | ||
| 10 : | collatz_sequence short list of maximum values : | ||
| 10 5 8 4 : | collatz_sequence_head : | ||
| 8 4 2 1 : | collatz_sequence_tail : | ||
| 6 : | collatz_sequence_length: | ||
| 10 5 8 4 2 1 : | Collatz_Sequence values : | ||
| Collatz_Sequence : | 10 5 8 4 2 1 |
Testcase , modified__Collatz_Sequence for integer 10 from Windows10 gui
| table 4, modified__Sequence for integer 10 | printed in tcl wiki format | ||
|---|---|---|---|
| 4: | |||
| 10.0 : | initial integer | ||
| 20.0 : | iteration limit , safety maybe cut short : | ||
| 4.0 : | optional index_tails for heads, max values, and tails, usually 4 : | ||
| 7 : | optional constant , nominal 1, calc reverts to number of calc steps : | ||
| 7 : | steps_iteration_total: | ||
| 16 : | collatz_sequence short list of maximum values : | ||
| 10 5 16 8 : | collatz_sequence_head : | ||
| 8 4 2 1 : | collatz_sequence_tail : | ||
| 7 : | collatz_sequence_length: | ||
| 10 5 16 8 4 2 1 : | Collatz_Sequence values : | ||
| Collatz_Sequence : | 10 5 16 8 4 2 1 |
Testcase , Partial Collatz_Sequence for integer 7 from Windows10 gui
| table 3, Regular Collatz_Sequences (3*N+1) for integer 7 from Windows10 gui | printed in tcl wiki format | ||
|---|---|---|---|
| quantity | value | value | comment, if any |
| 3: | testcase_number | ||
| 27.0 : | initial integer | ||
| 120.0 : | iteration limit , safety maybe cut short : | ||
| 4.0 : | optional index_tails for heads, max values, and tails, usually 4 : | ||
| 112 : | optional constant , nominal 1, calc reverts to number of calc steps : | ||
| 112 : | steps_iteration_total: | ||
| 9232 : | collatz_sequence short list of maximum values : | ||
| 27 82 41 124 : | collatz_sequence_head : | ||
| 8 4 2 1 : | collatz_sequence_tail : | ||
| 112 : | collatz_sequence_length: | ||
| Collatz_Sequence : | 27 82 41 124 62 31 94 47 142 71 214 107 322 161 484 242 121 364 182 91 274 137 412 206 103 310 155 466 233 700 350 175 526 263 790 395 1186 593 1780 890 445 1336 668 334 167 502 251 754 377 1132 566 283 850 425 1276 638 319 958 479 1438 719 2158 1079 3238 1619 4858 2429 7288 3644 1822 911 2734 1367 4102 2051 6154 3077 9232 4616 2308 1154 577 1732 866 433 1300 650 325 976 488 244 122 61 184 92 46 23 70 35 106 53 160 80 40 20 10 5 16 8 4 2 1 |
Appendix TCL programs and scripts
Pretty Print Version
Main Deck
proc collatz_sequence {number iteration} {
# Check parameter
if {!([string is wideinteger $number] && $number > 0)} {
error "Number '$number' is not positiv integer!"
}
if {!([string is wideinteger $iteration] && $iteration > 0)} {
error "Iteration '$iteration' is not positiv integer!"
}
# Initialisation
set sequence [list $number]
# Interations
for {set n 0} {$n <= $iteration} {incr n} {
if {$number == 1} {
return $sequence
}
if {$number % 2} {
# Odd
set number [expr {(3 * $number) + 1}]
} else {
set number [expr {$number / 2}]
}
lappend sequence $number
}
# After value reach 1 it is a endless sequence of 4 2 1 4 2 1 ...
# If we reach not 1 during the given ammount of iteration
# we raise an error to signal that number of iterations are to small
# or we reach the case all looking for.
error "Number of iteration '$iteration' reached without getting 1!"
}Pseudocode and Equations Section
#pseudocode can be developed from rules of thumb.
#pseudocode: some problems can be solved by proportions (rule of three), to some order of magnitude
#pseudocode: enter quantity1, quantity2, quantity3 and expected output (quantity4) for testcases.
#pseudocode: enter time in years, number of remaining items
#pseudocode: output fraction of (remaining items) over (items at time zero)
#pseudocode: ouput remaining items as fraction or percent
#pseudocode: output fraction of (quantity4 ) over ( quantity1 at time zero)
#pseudocode: output fraction of (quantity2) * (quantity3 ) over (quantity1 at time zero)
#pseudocode: outputs should be in compatible units.
#pseudocode: rules of thumb can be 3 to 15 percent off, partly since g..in g..out.
#pseudocode: need test cases > small,medium, giant
#pseudocode: need testcases within range of expected operation.
#pseudocode: are there any cases too small or large to be solved?
; Terence Tao realized that the Collatz conjecture was similar to partial differential equations.
; The Tao starting sample weighs toward numbers that
; have a remainder of 1 after being divided by 3,
; and away from numbers that have a remainder of 2 after being divided by 3.
; TCL pseudocode
; remove all numbers divisible by 3 on a list of integers,
; find all numbers that have a remainder of 1, when divided by 3.FeedBack Section
gold 8/24/2023 Thanks to all for your comments. I have added the feedback png's. As one can appreciate, we are approaching the asymptotic limit of high school algebra, some 50 years ago.
X-Non >>>>>>> 8/24/2023 >>>>>>>
All this is quite interesting! ...
The most intriguing attachment is the one about Collatz sequence or Hailstone sequence. So, for example, if one considers only the odd numbers in the sequence generated by a Collatz sequence, then each odd number is on average 3/4 of the previous one. (More precisely, the geometric mean of the ratios of outcomes is 3/4, which I believe correlates to your attachment's discussion that "the growth between successive odds is 3/4"). So, I would add that this also yields a heuristic argument establishing that every Collatz sequence should decrease in the long run, although there is no evidence against other cycles, but only against divergence. Nevertheless, the argument is not a proof because it assumes that Collatz sequences are assembled from uncorrelated probabilistic events, as you already implicitly indicate in your attachment. (But, it does rigorously establish, for instance, that the 2-adic extension of the Collatz process has 2 division steps for every multiplication step for almost all 2-adic starting values.) Under this scenario, a 2-adic will have 2 as the prime number p in a p-adic extension of rational numbers which is distinct from the real numbers, even though with some similar properties; the p-adic numbers can be written in a form similar to (possibly infinite) decimals, but with digits based on a prime rather than a composite number, and extending (possibly infinitely) to the left rather than to the right. So, given any prime number p, a p-adic number can be defined as a series
{\displaystyle s=\sum _{i=k}^{\infty }a_{i}p^{i}=a_{k}p^{k}+a_{k+1}p^{k+1}+a_{k+2}p^{k+2}+\cdots }
where k is an integer (possibly negative), and each a_{i} is a integer such that {\displaystyle 0\leq a_{i}<p.} Besides, a p-adic integer is a p-adic number such that {\displaystyle k\geq 0.} In general, the series that represents a p-adic number is not convergent in the usual sense, but it is convergent for the p-adic absolute value {\displaystyle |s|_{p}=p^{-k},} where k is the least integer i such that {\displaystyle a_{i}\neq 0} (if all a_{i} are zero, one has the zero p-adic number, which has 0 as its p-adic absolute value).
gold 8/24/2023, Not sure the math expressions display properly here. Maybe work around png's would be useful.
gold 4/11/2024 Update. Thanks for feedback. You have given a tiny spark of an idea. The tail end of the Collatz function descending to terminus might imply a delta trajectory in closing, that possibly could be related to the Exponential Doubling Function. Given the theory and papers from Idriss J. Aberkane, the Collatz trajectories using Base 3 generate a geometric cone like figure, as pixed. I might point that to test compatibility with Tcllib, I do test homebrew code loaded in the local laptop copy of Tcllib math and associated libraries. This is a local setup for ActiveState TCL on Windows10, so references to a my local TCLLIB::math library would not be portable. As one can appreciate, we are approaching the asymptotic limit of high school algebra, some 50 years ago. Many thanks to arjen & Andreas Kupries for the heavy lifting Tcllib Thanks to all for your comments.
Hidden Comments Section
Please include your wiki MONIKER and date in your comment with the same courtesy that I will give you. Thanks, gold 12Aug2020
HE 2021-09-11: Hello Gold, I have a bunch of suggestions/questions about the code. Mainly in respect to other operating systems but, also if one is using your code in a win10 or related system. This is not to bother you.
As far as I understand your code is planned to be executed on a command line. There is no input. And, output is completely done by using 'puts'. It also use only commands/procedures provided by a Tcl only installation (beside some lines I will discuss below). That means the code should be possible to execute everywhere where we can call a tclsh and copy or source the code into it.
Poorly this doesn't work. Because the code contains "package require Tk" without using any GUI and some installation will not have a Tk. And using the command 'console' which is only available in wish.exe but not in wish compiled for Linux, for example.
For sure some could simply copy the code between "package require Tk" and the usage of 'console' at the end to try to get it running. That will not work because there is a 'console show' in between. This needs also to be excluded. At the end the user interested of the result of your script needs to investigate the code to get it running. A bit inconvenience from my point of view. Particularly because all the problematic lines are mainly for eye candy only.
How would I try to execute this type of scripts: On win10 I would open a wish. It displays a console window. I would make a copy and past (c&p) of the code into this console window. The output would be crude to read because of:
- all the output before "proc table_format_out ..." would not be easy to read because the 'puts' lines and the output are interchanging.
- The change of font and geometry left a console window far to big on some displays and not able to show the text in a readable way. At least not for me.
- I don't discuss the format of the able output here, because this also not help to read the results.
Next try would be to open a tclsh on win10 and c&p the code into it. The result is similar. The font size and console background can't be changed so it is more comfortable to read. But the other issues mentioned above still exists and in addition we have the error message in between about the 'console' command.
Next try would be to store it in a file, start a tclsh on win10 (because "package require Tk" let me think it is planned to do so) and source the file into it. This simply raise a "Invalid command name "console"". This will be the same on Linux.
Next try would be to start a wish on win10 and source the stored file into it. I think that is the result you wanted. But, eye candy for you on your computer doesn't fit well on my computer. You also don't know if the user will have problems with a green background. And a smaller font size would show more from the table. At least on the computer I tried your code.
Now I tried all four variants on Linux. Sourcing the file lead in both cases to error message "invalid command name "console"" without any other output. C&p into a wish or tclsh lead to the ugly output where it is not clear where to look for the wanted result.
What I would change:
- To be platform independent I would remove "package require Tk" and the 'console' lines.
- To be able to run it by double-click inside win10 I would add somewhere at the top of the script:
if {$tcl_platform(platform) == {windows}} {
console show
}- I would put all output into one procedure so that the last command could this procedure and afterwards all output is generated.
Sorry again, for all the comments only because of output and executing. I tend to write to much in case I try to explain my view. But look how easy it is to make the code run in 8 different conditions instead only running under one condition.
Until here, I read so often this piece of code that I found some small other items:
- Procedures isPositive and isNegative are not used. Perhaps, isPositive was planned to be used in collatz_sequence as a protection not to use negative numbers?
- "set tclprecision 17" is used. The Tcl 8.6 documentation tells "It defaults to 0. Applications should not change this value;". I'm not sure to understand why it is used. The whole math of that problem should be integer calculation. At least until the limit of 8 byte integer is crossed. And as long as no fraction is forced the math should stay integer. Perhaps, I'm wrong. But, that is I understood how Tcl calculation works.
- Where you are using the math packages you load in the beginning? I can't find the usage of it. I would understand "package require math::bignum" to be able to calculate behind the 8 byte integer limit. But the named one?
HE 2021-09-12: Since my comment yesterday, all comment lines are changed from '#' to ';#' at the beginning. Is there a reason for this? From my knowledge a ';' is not need for a proper comment at the beginning of a line. Only if the comment is behind a command on the same line a ';' is needed before the '#' to separate both commands.
HE 2021-09-12: As an answer of your question on Ask, and it shall be given # 13 here my version of collatz_sequence based on your one. For loop provide everything to control iteration. Some tests in the beginning to assure that positive integers are used for number and iteration. That makes it easier to stop as we find 1 as a result. At least the first 10 million integer I tried to use for number will all end with 1 and then go to the endless sequence. As far as I understood others are tried far higher numbers with the same end. Also I would not check separately for odd and even. One check is enough. And I used the expression itself instead of put it into a separate procedure. This will spare calculation power with bigger numbers.
Main Deck
proc collatz_sequence {number iteration} {
# Check parameter
if {!([string is wideinteger $number] && $number > 0)} {
error "Number '$number' is not positiv integer!"
}
if {!([string is wideinteger $iteration] && $iteration > 0)} {
error "Iteration '$iteration' is not positiv integer!"
}
# Initialisation
set sequence [list $number]
# Interations
for {set n 0} {$n <= $iteration} {incr n} {
if {$number == 1} {
return $sequence
}
if {$number % 2} {
# Odd
set number [expr {(3 * $number) + 1}]
} else {
set number [expr {$number / 2}]
}
lappend sequence $number
}
# After value reach 1 it is a endless sequence of 4 2 1 4 2 1 ...
# If we reach not 1 during the given ammount of iteration
# we raise an error to signal that number of iterations are to small
# or we reach the case all looking for.
error "Number of iteration '$iteration' reached without getting 1!"
}Hidden Comments Section
gold 9/30/2021. Thinking point from Alex post. It looks like what you've written is: "pick a random number x (nevermind that there's no uniform distribution on N), then with the expectation probability(x) is 1/2, it is even and 1/2, that it's odd. Now, you're right that P(x)=(1/2)*P(x/2)+(1/2)*P(3*x+1). But P(x) is NOT constant.
E(3) ~? expr { (1/2.)*(3/2.) + (1/2.)*(3*3.+1.) }, 5.75?
E(4) ~? expr { (1/2.)*(4/2.) + (1/2.)*(3*4.+1.) }, 7.5?
E(1) ~? expr { (1/2.)*(1/2.) } , 0.25 ???
E(2) ~? expr { (1/2.)*(2/2.) } , 0.5 ???
E(3) ~? expr { (1/2.)*(3/2.) } , 0.75 ???
E(4) ~? expr { (1/2.)*(4/2.) } , 1. ???
E(5) ~? expr { (1/2.)*(5/2.) } , 1.25 ???gold 9/30/2021. For the example of integer is 3. The probability(x) that x is even and P(3) approximates { (1/2.)*(3/2.) } returns 0.75. The complement probability that P(x) is not even and is something else (not x/2) approximates expr { 1.- (1/2.)*(3/2.) } returns 0.25. The Expectation E(3) or sum of joint probability for two games as even and odd results is expr { 0.75 + 0.25}, 1.0. The general E(P(N) formula over the total games until finish is formula E(P(N)) = expr {1. - (1./2.)**$N} . ???? < formula E(K)*(P(N)) ~?? expr { K * ( 1. - (1./2.)**$N )} The more games, the closer the (P(N)) approaches 1. The more games, the closer E(K) approaches and approximates expr { K * P(N)} . > ?????
Please include your wiki MONIKER and date in your comment with the same courtesy that I will give you. Thanks, gold 12Sep2021 Works with: Tcl version 8.5 Use the {*} expansion operator to substitute the list value with its constituent elements
package require Tcl 8.5
set values {4 3 2 7 8 9} ::tcl::mathfunc::max {*}$values ;# ==> 9
Draft. The Collatz Sequence has several applications and implications in mathematics and computer science:
1. Number Theory: The Collatz Conjecture, which states that the sequence will always reach the number 1 regardless of the starting integer, remains an unsolved problem in mathematics. Studying the properties of the Collatz Sequence can lead to insights into number theory and the behavior of integers.
2. Algorithm Analysis: The Collatz Sequence is often used as a benchmark for testing algorithms and computational methods. Analyzing the sequence can help researchers understand the efficiency and complexity of different algorithms.
3. Cryptography: The Collatz Sequence has been used in certain cryptographic algorithms and protocols. Its unpredictable nature and iterative properties make it a potential candidate for generating random sequences or cryptographic keys.
4. Chaos Theory: The Collatz Sequence exhibits chaotic behavior, with seemingly random fluctuations and patterns. Studying the dynamics of the sequence can provide insights into chaos theory and nonlinear systems.
5. Educational Purposes: The Collatz Sequence is often used as a teaching tool in mathematics and computer science courses. It can help students understand concepts such as recursion, iteration, and mathematical reasoning.
Overall, the Collatz Sequence serves as a fascinating and versatile mathematical concept with applications in various fields of study. Its simplicity and complexity make it a valuable tool for exploring mathematical patterns and phenomena.
Draft. Collatz sequences, also known as the "3n + 1" problem, have applications in various fields, including mathematics, computer science, and cryptography. Here are some examples of their applications:
1. Mathematical research: Collatz sequences have been a subject of interest in number theory and combinatorics. Researchers study the behavior of these sequences, trying to determine if they always reach 1 for any given starting number, or if there are any patterns or properties that can be derived from them.
2. Cryptography: Collatz sequences have been used in the design of cryptographic algorithms and protocols. The unpredictable nature of these sequences can be exploited to create secure encryption schemes, random number generators, and hash functions.
3. Computer Science: Collatz sequences are a popular example of a simple algorithm that can be implemented on a computer to demonstrate the power and limitations of computational methods. They are often used as a benchmark for testing the efficiency of programming languages and algorithms.
4. Artificial Intelligence: Collatz sequences can be used in the development of artificial intelligence algorithms. For example, researchers have used them to study the behavior of neural networks and to develop algorithms for solving complex problems.
5. Education: Collatz sequences are a great tool for teaching basic concepts in mathematics and computer science. They can be used to introduce students to algorithms, recursion, and problem-solving techniques.
Collatz sequences have a wide range of applications in mathematics, computer science, and cryptography, making them an interesting and important topic for research and study.
test! seems to work
gold 9/11/2021. first edit XXS
gold 9/12/2021. replaced original proc with HE proc, dropped extraneous procs isPositive, isNegative, isOdd, and isEven as confusing to readers. Procs still on ticket if feasible for TCLLIB. In 2020, starting integer values up to 2**268 approximating 2.95*1020 and associated sequences have been checked in the Collatz conjecture. Yes, one would need math::bignum package for that and to check all speed savings on supporting integer procs for Collatz sequences at that size. x
gold 9/13/2021. added modified_collatz_sequence formulas, replaced :# with #.
gold 9/13/2021. forwarded ticket on collatz_sequences to TCLLIB. I have loaded the ticket e035b93f363dc62153375b77ad3bcf339a68d407 Title: Collatz_Sequence, modified_Collatz_Sequence, posiitve & negative logic test for integers.
gold 9/21/2021. Forwarded query to ActiveState on percentage of Unix users vs PC vs Apple. Received PM. quote " ActiveTcl users are overwhelmingly on Windows (80% or so), and tend to have a high proportion of novice to intermediate users. "
| Category Numerical Analysis | Category Toys | Category Calculator | Category Mathematics | Category Example | Toys and Games | Category Games | Category Application | Category GUI |