Divisible by 7
Keith Vetter 2016-04-18 -- How can you quickly determine if a number is evenly divisible by 7? There are nice tricks for 2, 3, 4, 5, 6, 8 and 9 but 7 is trickier.
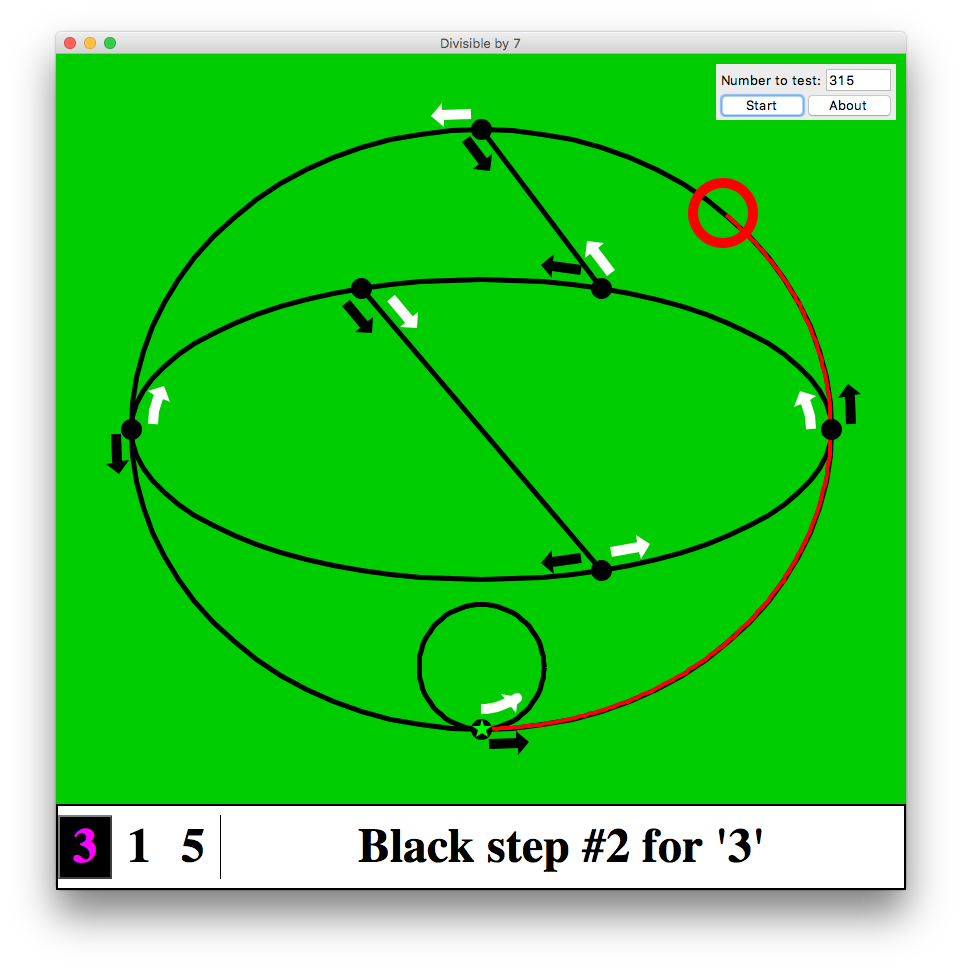
Here's a simple, graphical way to test for divisibility by seven. Start at the starred node at the bottom. Now take each digit in turn from left to right in your number. For each digit, follow that many black arrows in a row, and then add one white arrow. If you finish at the bottom, then your number is divisible by 7.
How does it work? Here's a hint: the white arrows correspond to 10x mod 7.
Jeff Smith 2019-04-21 : Below is an online demo using CloudTk
##+########################################################################## # # 7div.tcl -- Animation to test for divisibility by 7 # by Keith Vetter 2013-08-07 package require Tk set PTS(0) {at 270 circle 0} set PTS(1) {at 0 circle 0} set PTS(2) {at 90 circle 0} set PTS(3) {at 70 circle 1} set PTS(4) {at 110 circle 1} set PTS(5) {at 290 circle 1} set PTS(6) {at 180 circle 0} set ARCS(0,black) {circle 0 to 1} set ARCS(0,white) {circle 2 to 0} set ARCS(1,black) {circle 0 to 2} set ARCS(1,white) {circle 1 to 3} set ARCS(2,black) {line 10 to 3} set ARCS(2,white) {circle 0 to 6} set ARCS(3,black) {circle 1 to 4} set ARCS(3,white) {line 10 to 2} set ARCS(4,black) {line 11 to 5} set ARCS(4,white) {line 11 to 5} set ARCS(5,black) {circle 1 to 6} set ARCS(5,white) {circle 1 to 1} set ARCS(6,black) {circle 0 to 0} set ARCS(6,white) {circle 1 to 4} set ARROW(0) {black_delta 8 15 white_delta 0 -20} set ARROW(1) {black_delta 20 -5 white_delta -20 0} set ARROW(2) {black_delta -15 10 white_delta -10 -15} set ARROW(3) {black_delta -20 -18 white_delta 10 -15} set ARROW(4) {black_delta -15 15 white_delta 30 10} set ARROW(5) {black_delta -20 -12 white_delta 10 -18} set ARROW(6) {black_delta -15 5 white_delta 22 -5} set S(rad,0,a) 350 set S(rad,0,b) 300 set S(rad,0,y) 0 set S(rad,1,a) 350 set S(rad,1,b) 150 set S(rad,1,y) 0 set d [expr {($S(rad,0,b) - $S(rad,1,b))}] set r [expr {$d * 5 / 12.0}] set S(rad,2,a) $r set S(rad,2,b) $r set S(rad,2,y) [expr {$S(rad,0,b) - $r}] set S(cross,10) {2 3} set S(cross,11) {4 5} set S(animate,stepSize) 5 set S(animate,delay) 20 set S(animate,extraDelay) 1000 set S(number,candidate) 315 set S(box) 10 set S(digits,font) {Times 48 bold} set S(breadcrumbs) 1 set S(w) [expr {2*$S(rad,0,a) + 150}] set S(h) [expr {2*$S(rad,0,b) + 150}] set S(state) unstarted proc DoDisplay {} { global S wm title . "Divisible by 7" frame .digits -bd 2 -relief solid -pady 3m pack .digits -side bottom -fill x ShowNumber $S(number,candidate) canvas .c -width $S(w) -height $S(h) -bd 0 -highlightthickness 0 -bg green4 bind .c <Configure> {CenterCanvas %W %w %h} pack .c -side top -fill both -expand 1 DrawOval 0 -width 5 DrawOval 1 -width 5 DrawOval 2 -width 5 DrawPoints DrawCrossing 10 -width 5 DrawCrossing 11 -width 5 DrawArrows -width 10 .c create oval [Box {*}$S(0,xy) 30] -tag animate -fill {} -width 10 -outline red ::ttk::frame .ctrl -padding 1m ::ttk::frame .ctrl.top ::ttk::label .ctrl.l -text "Number to test:" ::ttk::entry .ctrl.e -textvariable ::S(number,candidate) -width 5 bind .ctrl.e <Key-Return> {.ctrl.test invoke} ::ttk::button .ctrl.test -text "Start" -command Start ::ttk::button .ctrl.about -text "About" -command About grid .ctrl.l .ctrl.e -sticky ew -in .ctrl.top grid columnconfigure .ctrl.top 1 -weight 1 pack .ctrl.top -fill x pack .ctrl.test .ctrl.about -expand 1 -side left place .ctrl -in .c -relx 1 -rely 0 -x -10 -y 10 -anchor ne } proc ShowNumber {number} { destroy {*}[winfo child .digits] set digits " " if {[string is integer -strict $number]} { set ::S(msg) "Testing if $number is divisible by 7" set digits $number } elseif {[string trim $number] eq ""} { set ::S(msg) "" } else { set ::S(msg) "$number is not an integer" } for {set i 0} {$i < [string length $digits]} {incr i} { set digit [string index $digits $i] label .digits.d$i -text $digit -font $::S(digits,font) pack .digits.d$i -side left } frame .digits.bar -bg black -padx 1 label .digits.msg -textvariable ::S(msg) -font $::S(digits,font) pack .digits.bar -side left -fill y pack .digits.msg -side left -fill both -expand 1 } proc HighlightDigit {how digits subIdx idx} { global S set w .digits.d$idx if {$how eq "over"} { if {$idx == 0} { set S(msg) "$digits is divisible by 7" } else { set S(msg) "$digits is not divisible by 7" } } elseif {$how eq "done"} { $w config -bd 0 -bg [lindex [$w config -bg] 3] } elseif {$how eq "begin"} { set digit [string index $digits $idx] $w config -bd 2 -relief raised -bg black -fg magenta .c itemconfig breadcrumbs -fill cyan -tag breadcrumbs,old set S(msg) "Processing digit '$digit'" return $S(animate,extraDelay) } elseif {$how eq "black"} { set digit [string index $digits $idx] incr subIdx set S(msg) "Black step #$subIdx for '$digit'" } elseif {$how eq "white"} { set digit [string index $digits $idx] $w config -bg white set S(msg) "White step for '$digit'" } else { error "unknown how: $how" } return 1 } proc ArcCoords {from color} { global S PTS ARCS lassign $ARCS($from,$color) type which . to if {$type eq "line"} { set xy [concat $S($from,xy) $S($to,xy)] } else { set startAngle [lindex $PTS($from) 1] set endAngle [lindex $PTS($to) 1] set xy [OvalCoords $which $startAngle $endAngle 5] } return $xy } proc ArrowCoords {from color distance} { global S ARCS set xy [ArcCoords $from $color] set axy {} set soFar 0 lassign $xy x0 y0 foreach {x1 y1} $xy { set leg [expr {hypot($x1-$x0, $y1-$y0)}] if {$soFar + $leg < $distance} { lappend axy $x1 $y1 set soFar [expr {$soFar + $leg}] } else { set short [expr {$distance - $soFar}] lassign [ResizeLine $x0 $y0 $x1 $y1 $short] x y lappend axy $x $y break } lassign [list $x1 $y1] x0 y0 } return $axy } proc LineLength {xy} { set total 0 lassign $xy x0 y0 foreach {x1 y1} $xy { set leg [expr {hypot($x1-$x0, $y1-$y0)}] set total [expr {$total + $leg}] lassign [list $x1 $y1] x0 y0 } return $total } proc SegmentLine {xy maxLen} { set segments {} lassign $xy x0 y0 set segment [list $x0 $y0] set segmentLength 0 for {set idx 2} {$idx < [llength $xy]} {incr idx 2} { lassign [lrange $xy $idx $idx+1] x1 y1 set leg [expr {hypot($x1-$x0, $y1-$y0)}] while {$segmentLength + $leg > $maxLen} { set short [expr {$maxLen - $segmentLength}] lassign [ResizeLine $x0 $y0 $x1 $y1 $short] x y lappend segments [concat $segment $x $y] set segment [list $x $y] set segmentLength 0 lassign [list $x $y] x0 y0 set leg [expr {hypot($x1-$x0, $y1-$y0)}] } lappend segment $x1 $y1 set segmentLength [expr {$segmentLength + $leg}] lassign [list $x1 $y1] x0 y0 } if {$segmentLength > 0} { lappend segments $segment } return $segments } proc ResizeLine {x0 y0 x1 y1 newLength} { set leg [expr {hypot($x1-$x0, $y1-$y0)}] set dx [expr {$x1 - $x0}] set dy [expr {$y1 - $y0}] set x [expr {$x0 + $dx * $newLength / $leg}] set y [expr {$y0 + $dy * $newLength / $leg}] return [list $x $y] } proc CenterCanvas {W w h} { set w [expr {$w / 2}] set h [expr {$h / 2}] $W config -scrollregion [list -$w -$h $w $h] } proc DrawOval {who args} { global S set xy [OvalCoords $who 0 360 5] .c create line $xy -tag oval$who {*}$args return "oval$who" } proc OvalCoords {who start end {delta 5}} { global S set a $S(rad,$who,a) set b $S(rad,$who,b) set y0 [expr {[info exist S(rad,$who,y)] ? $S(rad,$who,y) : 0}] set xy {} # Which direction set clockwise [expr {($end - $start) % 360}] set anticlockwise [expr {($start - $end) % 360}] set dir [expr {$clockwise <= $anticlockwise ? "clockwise" : "anticlockwise"}] if {$dir eq "anticlockwise"} { lassign [list $start $end] end start } if {$end <= $start} { incr end 360 } for {set deg $start} {$deg <= $end} {incr deg $delta} { set rad [expr {acos(-1) * $deg / 180}] set x [expr {$a * cos($rad)}] set y [expr {$y0 - $b * sin($rad)}] set x [format %.2f $x] set y [format %.2f $y] if {$dir eq "anticlockwise"} { set xy [concat $x $y $xy] } else { lappend xy $x $y } } return $xy } proc DrawArrows {args} { global S for {set who 0} {$who < 7} {incr who} { set dx0 0 ; set dy0 0 ; set dx1 0 ; set dy1 0 lassign $::ARROW($who) . dx0 dy0 . dx1 dy1 set xy [ArrowCoords $who black 40] set id [.c create line $xy -tag arrow,$who,black -fill black -arrow last -arrowshape {12 12 7} {*}$args] .c move $id $dx0 $dy0 set xy [ArrowCoords $who white 40] set id [.c create line $xy -tag arrow,$who,white -fill white -arrow last -arrowshape {12 12 7} {*}$args] .c move $id $dx1 $dy1 } } proc DrawPoints {} { global S for {set i 0} {$i < 7} {incr i} { #lassign $S($i) who degree lassign $::PTS($i) . degree . whichOval set a $S(rad,$whichOval,a) set b $S(rad,$whichOval,b) set S($i,xy) [PointOnEllipse $degree $a $b] .c create oval [Box {*}$S($i,xy) $S(box)] -fill black -tag [list points p$i] } set id [.c create poly [MakeStar {*}$S(0,xy) $S(box)] -fill green1 -tag {points p0}] .c move $id 1 0 } proc DrawCrossing {who args} { set xy [CrossingCoords $who] .c create line $xy {*}$args } proc CrossingCoords {who} { global S lassign $S(cross,$who) node1 node2 return [concat $S($node1,xy) $S($node2,xy)] } proc Box {x y r} { return [list [expr {$x-$r}] [expr {$y-$r}] [expr {$x+$r}] [expr {$y+$r}]] } proc PointOnEllipse {degree a b} { set rad [expr {acos(-1) * $degree / 180}] set x [expr {$a * cos($rad)}] set y [expr {-$b * sin($rad)}] set x [expr {round($x)}] ; set y [expr {round($y)}] return [list $x $y] } proc MakeStar {x y delta} { set pi [expr {acos(-1)}] # Compute distance to inner corner #set x1 [expr {$delta * cos(54 * $pi/180)}] ;# Unit vector to inner point set y1 [expr {sin(54 * $pi/180)}] set y2 [expr {$delta * sin(18 * $pi/180)}] ;# Y value to match set delta2 [expr {$y2 / $y1}] # Now get all coordinates of the 5 outer and 5 inner points for {set i 0} {$i < 10} {incr i} { set d [expr {($i % 2) == 0 ? $delta : $delta2}] set theta [expr {(90 + 36 * $i) * $pi / 180}] set x1 [expr {$x + $d * cos($theta)}] set y1 [expr {$y - $d * sin($theta)}] lappend coords $x1 $y1 } return $coords } proc About {} { set msg "7 Graphical Divisibility Test\nby Keith Vetter -- April, 2016\n\n" append msg "Here's a simple, graphical way to test for divisibility by seven.\n\n" append msg "Start at the starred node at the bottom. Now take each digit in turn " append msg "from left to right in your number. For each digit, follow that many " append msg "black arrows in a row, and then add one white arrow. If you finish at " append msg "the bottom, then your number is divisible by 7.\n\n" append msg "How does it work? Here's a hint: the white arrows correspond to 10x mod 7." tk_messageBox -message $msg } namespace eval ::Animate {} proc ::Animate::StepsForLeg {whichNode idx digits} { global ARCS set digit [string index $digits $idx] set steps {} lappend steps "begin" [list - $idx] for {set i 0} {$i < $digit} {incr i} { lappend steps "black" [list $i $idx] lappend steps {*}[::Animate::Xy2Steps [ArcCoords $whichNode black]] set whichNode [lindex $ARCS($whichNode,black) 3] } lappend steps "white" [list - $idx] lappend steps {*}[::Animate::Xy2Steps [ArcCoords $whichNode white]] lappend steps "done" [list - $idx] set whichNode [lindex $ARCS($whichNode,white) 3] return [list $whichNode $steps] } proc ::Animate::Xy2Steps {xy} { global S set segments [SegmentLine $xy $S(animate,stepSize)] set steps [lrange [lindex $segments 0] 0 1] set steps {} foreach segment $segments { lappend steps {*}[lrange $segment end-1 end] } return $steps } proc Start {} { global S set S(number,candidate) [string trim $S(number,candidate)] if {$S(state) eq "unstarted"} { ResetAnimation set S(state) started 7Test $S(number,candidate) } else { set S(state) unstarted } } proc 7Test {digits} { ShowNumber $digits if {[string is integer -strict $digits]} { DoAnimation $digits 0 {} 0 } else { set ::S(state) "unstarted" } } proc ResetAnimation {} { .c delete breadcrumbs breadcrumbs,old .c coords animate [Box {*}$::S(0,xy) 30] } proc DoAnimation {digits idx steps where} { global S if {$S(state) ne "started"} return if {$steps eq {} && $idx >= [string length $digits]} { HighlightDigit "over" $digits - $where set S(state) "unstarted" return } set nextWhere $where if {$steps eq {}} { set digit [string index $digits $idx] lassign [::Animate::StepsForLeg $where $idx $digits] nextWhere steps incr idx } set extraDelay 1 if {$steps ne {}} { set nextSteps [lassign $steps newX newY] if {$newX in {"begin" "black" "white" "done"}} { set extraDelay [HighlightDigit $newX $digits {*}$newY] } else { lassign [.c bbox animate] x0 y0 x1 y1 set x [expr {($x1 + $x0)/2}] ; set y [expr {($y1 + $y0)/2}] set dx [expr {$newX - $x}] ; set dy [expr {$newY - $y}] if {$S(breadcrumbs)} { set xy [.c coords breadcrumbs] if {$xy eq {}} { .c create line $x $y $x $y -tag breadcrumbs -fill red -width 4 .c raise points .c raise animate } else { lappend xy $x $y .c coords breadcrumbs $xy } } .c move animate $dx $dy } set delay $S(animate,delay) if {$extraDelay > 1} { set delay $extraDelay } after $delay [list DoAnimation $digits $idx $nextSteps $nextWhere] } return } ################################################################ DoDisplay return