General Tianji' Horse Race Strategy from China and eTCL demo example calculator, numerical analysis
General Tianji' Horse Race Strategy from China and eTCL demo example calculator, numerical analysis
This page is under development. Comments are welcome, but please load any comments in the comments section at the bottom of the page. Please include your wiki MONIKER and date in your comment with the same courtesy that I will give you. Aside from your courtesy, your wiki MONIKER and date as a signature and minimal good faith of any internet post are the rules of this TCL-WIKI. Its very hard to reply reasonably without some background of the correspondent on his WIKI bio page. Thanks, gold10Dec2018
- General Tianji' Horse Race Strategy from China and eTCL demo example calculator, numerical analysis
- Preface
- Introduction
- Pseudocode Section
- Appendix Code
- Console program for race output as CVS spreadsheet, includes > equal probability horses <
- cvs output for > wins only < of horse_c
- Console program for tianji horse race and combined unequal probability
- output follows for list of winners in trial races with three 3 heats, > unequal probability horses <
- Example eTCL code for selecting winners for random horses in a race
- Example eTCL code for horse accidents or shortfalls
- Comments Section
Preface
gold Here is some eTCL starter code for General Tianji' Horse Race Strategy from China in calculator shell. Additional console programs below are used to check or improve subroutines in calculator shell.
Introduction
Here is the contrarian viewpoint of General Tianji' Horse Race Strategy from China in calculator shell. Both the King and General Tianji have sets of 3 horses. Each set of three horses has low grade horse, middle grade horse and best grade horse. As a contrarian strategy, Sun Bin advised that the General Tianji run the General's low grade horse against the King's best grade horse, the General's middle grade horse against the King's low grade horse, and the General's best grade horse against the King's middle grade horse. The result was that all three of the General Tianji 's horses won that day circa 500 BCE. Each round of the horse race won 200 silver dollars. General Tianji and General Sun Bin's share of the winnings was a big bag of silver, worth expr{3*$200} or 600 silver dollars. When this bit of strategy was explained later to the King, the King promoted General Tianji to chief of all armies and promoted Sun Bin to General and military strategy advisor of General Tianji. Not sure an elegant proof can be drummed up, but there are many random horses in TCL. This racehorse problem can be loaded into the TCL calculator shell and each horse of three heats can be simulated with a random race score. The TCL calculator from the Random Walk Equation offers some analogies.
Contrarian Strategy has Many Applications
The contrarian strategy of General Sun Bin and General Tianji has been a favorite topic among Chinese scholars and war colleges for over 2500 years. Contrarian strategy has many applications. The name Tianji is believed to mean literally “heaven gold “ or “gold from heaven” in Chinese. Typically the ancient battle lines in both East and West grouped the army and commanders into three sections, 1) left wing (weakest) , 2) center (strongest) , and 3) right wing (middle grade). Adapting the contrarian Tianji strategy to the ancient battle ranks, put the weakest unit against the strongest opposition in the center, put the strongest unit against the middle opposition (presumed right wing), and put the middle strength unit against the weakest opposition (presumed left wing).
Not familiar with the Chinese ancient battles, but this contrarian strategy was the favorite tactic of General Hannibal and won the greatest victories against Rome in the Punic wars. At the battle of Cumae (Italy), General Hannibal deliberately collapsed his center as the weakest force, allowing his stronger left and right forces to attack the Roman forces from the side and rear. Note that in some modern warfare, the strongest unit in the center against heavy entrenched opposition does not progress and effectively loses. Some modern battles are actually won by arriving first at the scene of a strategic point and by outflanking the opposition. This contrarian strategy is also used in man to man combat (kung fu, tai chi fist, tai chi sword). One common strategy in martical is to retreat in the center file and save the strongest blows in advancing to the side files, as the tai chi circular motion of side strikes and strikes to the rear.
Expected Wins for Different Grades of Horses
The tale of the General Tianji and General Sun Bin ( died 316 BCE) was found in the Chinese history book, Shujing. The Shujing history book was literally saved from the flames of the book burning during first Chinese empire. I have a very rare English translation of the Shichih (sic) commentary in my library. Here the particular issue was how the grades of horses were defined in ancient China. The analysis assumed the best grade horse won 50 percent of his races, the middle grade won 35 percent, and the low grade won 15 percent. The TCL calculator has entries for the grade probabilities to be changed so the effects or rewards of better or lesser random models can be studied.
An alternate method for selecting winners for random horses is somewhat like the sieve method or throwing different colored apples into separate buckets for each horse. The output of the random generator is a decimal fraction between 0.0 and 1.0. Each random horse is assigned a range or band between 0.0 and 1.0, or between the equivalent 0 percent and 100 percent probability. Meaning, the developed formula is 100 percent times the probability of the variable 1.0 from the generator. For example, random horse_a could be assigned the band 0 to 20 percent, random horse_b could be assigned 20 to 30 percent, and random horse_c could be assigned 50 to 100 percent. In different expressions, the probability bands for the horses are 0. > horse_a < 20. , 20> horse_b < 50., and 50. > horse_c < 100.
The strategy of General Tianji is very good for this type of problem and I would not like to bet against General Tianji. However, in this calculator the horses are random and their performance is uncertain. Meaning on the start gun or solve button, the individual horses may not win every heat and every purse for General Tianji. In working the calculator a number of times, the King may win a race and there were rare occasions where the King won all three races. The strategy of General Tianji can only be proved over a certain cumulative number of races, probably >> 50 races.
Code Extensions for Racehorses
Some trial code for racehorse accidents or racehorse troubles can be developed for random horses. For the example below, there is a 15 percent chance of hoof infection. If the statement on hoof infection fires, there is a 0.1 factor or 10 percent loss as short_fall of the finish line or 10 percent reduction in normal horse speed. Also, horse speed may not be constant, so a different exponential curve or exponential constant could be selected, reduced, or changed for the horse speed. Notice the potential loss for the horse is calculated independent of whether the hoof infection flag is yes or no (0 or 1). The potential for trouble is there whether or not the accident actually occurs. The potential for trouble can be calculated, so strategy or insurance can be adjusted for the horse race. And as a follow-on hint for the interested student, there is an application for the Tainji strategy in the modern insurance industry.
It is possible to handicap random horces. Suppose 2 low grade horses were rated at 15 percent probability. Setting the random scores for each low grade horse for between boundaries of 0 and 15 percent. There should be an equal probability in the random selection of a score between 0 and 15 percent for each horse. Now consider a low grade horse rated at 15 percent ran against a medium grade horse rated at 35 percent. In most cases, the random selection of a low grade horse score between 0 and 15 percent would lose to a random selection of a medium grade horse score between 0 and 35 percent. We can make the race of low and medium grade more fair by introducing a handicap factor. In the code, one can either add 20 percent to the low grade horse rating or subtract 20 percent to the medium grade horse rating. The calculator has run out of slots on the external display, but internal commands for { set $low + $low 20 } and { set $medium - $medium 20} should be easy in a local copy of the TCL program.
Conclusions
Over the years, the Tainji horserace as a computer contest problem is featured in international ACM student contests with an average of 6000 Chinese entries ( computer programs ). Most of the entries featured bipartite matching algorithms. For the TCL calculator, the calculator is returning the results of random models so the random results are not always the same with each solve. Over a number of cases, the cumulative or average results should approach the results or winnings of General Tianji. And the author is betting that bag of silver to fall from heaven (translated tian jin)!
Pseudocode Section
# using pseudocode
proc test1 {
# possible problem instances,
low vs high
middle vs low
high vs middle}
proc test2 {
initialize algorithm_result = 1.
initialize terms of tianji combined probability
proc test3 {
combined probability of winning as tianji_win_prob
tianji_win_prob has terms of unequal probability
proc test4 {
use llength(lsearch)/llength winner list
to calculate probilities of
1) prob_1(tianji_low vs king_high) horses
2) prob_2(tianji_middle vs king_low) horses
3) prob_3(tianji_high vs king_middle)} horses
proc test5 {
prob_1 = tianji high probability * [expr { rand() } ]
prob_2 = tianji medium probability * [expr { rand() } ]
prob_3 = tianji low probability * [expr { rand() } ]
would need ~100 trials for answer to gel, in iterative solution }
proc test6 {
check algorithm
f(solution) =? initial product
check_sum = a+b+c+d+e
set answers and printout with resulting values
pseudocode: need test cases > small,medium, giant
pseudocode: need testcases within range of expected operation.
pseudocode: are there any cases too small or large to be solved?
pseudocode: limit to size of eTCL list, ref versions. }
#end of fileTestcases Section
In planning any software, it is advisable to gather a number of testcases to check the results of the program. The math for the testcases can be checked by pasting statements in the TCL console. Aside from the TCL calculator display, when one presses the report button on the calculator, one will have console show access to the capacity functions (subroutines).
Testcase A1
| table 1 | printed in | tcl wiki format |
|---|---|---|
| quantity | value | comment, if any |
| 1: | testcase_number | |
| 50.0 : | high grade horse probability percent (a) , usually 50 | |
| 35.0 : | medium grade horse probability percent (b) , usually 35 | |
| 15.0 : | low grade horse probability percent (c) , usually 15 | |
| 1.0 : | optional: | |
| 1.0 : | optional: | |
| 1.0 : | optional: | |
| 3.0 : | optional: number Tianji wins, 0 to max 3 | random results |
| 600.0 : | answer: total winnings silver dollars | random results |
Testcase A2
| table 1 | printed in | tcl wiki format |
|---|---|---|
| quantity | value | comment, if any |
| 2 : | testcase_number | |
| 50.0 : | high grade horse probability percent (a) , usually 50 | |
| 30.0 : | medium grade horse probability percent (b) , usually 35 | |
| 20.0 : | low grade horse probability percent (c) , usually 15 | |
| 1.0 : | optional: | |
| 1.0 : | optional: | |
| 1.0 : | optional: | |
| 1.0 : | optional: number Tianji wins, 0 to max 3 | random results |
| 200.0 : | answer: total winnings silver dollars | random results |
Testcase A3
| table 3 | printed in | tcl wiki format |
|---|---|---|
| quantity | value | comment, if any |
| 3 : | testcase_number | |
| 50.0 : | high grade horse probability percent (a) , usually 50 | |
| 40.0 : | medium grade horse probability percent (b) , usually 35 | |
| 10.0 : | low grade horse probability percent (c) , usually 15 | |
| 1.0 : | optional: | |
| 1.0 : | optional: | |
| 1.0 : | optional: | |
| 1.0 : | optional: number Tianji wins, 0 to max 3 | random results |
| 200.0 : | answer: total winnings silver dollars | random results |
Testcase 1
| table 1 | printed in | tcl wiki format |
|---|---|---|
| quantity | value | comment, if any |
| 1: | testcase_number | |
| 50.0 : | high grade horse probability percent (a) , usually 50 | |
| 35.0 : | medium grade horse probability percent (b) , usually 35 | |
| 15.0 : | low grade horse probability percent (c) , usually 15 | |
| 200.0 : | Optional: Tianji bets on each heat (usually 200 silver dollars ): | |
| 3.0 : | answers: check sum all wins =? 3 : | |
| {heat_1 tl?kh win? 0.809 4.6 0. } { heat_2 tm?kl win? 10.2 14.5 0. } { heat_3 th?km win? 40.4 25.3 1. } : | list of horse race scores | |
| 0. logic : | tianji_low_horse_win logic, 0 or 1 | |
| 0. logic : | tianji_medium_horse_win logic, 0 or 1 | |
| 1. logic : | tianji_high_horse_win logic, 0 or 1 | |
| 2.0 : | number king wins, 0 to max 3 | random results |
| 1.0 : | number Tianji wins, 0 to max 3 | random results |
| 200.0 : | total winnings for Tianji silver dollars | random results |
Testcase 2
| table 2 | printed in | tcl wiki format |
|---|---|---|
| quantity | value | comment, if any |
| 2: | testcase_number | |
| 50.0 : | high grade horse probability percent (a) , usually 50 | |
| 30.0 : | medium grade horse probability percent (b) , usually 35 | |
| 20.0 : | low grade horse probability percent (c) , usually 15 | |
| 200.0 : | Optional: Tianji bets on each heat (usually 200 silver dollars ): | |
| 3.0 : | answers: check sum all wins =? 3 : | |
| {heat_1 tl?kh win? 14.9 21.6 0. } { heat_2 tm?kl win? 9.4 13.5 0. } { heat_3 th?km win? 26.9 24.7 1. } : | list of horse race scores | |
| 0. logic : | tianji_low_horse_win logic, 0 or 1 | |
| 0. logic : | tianji_medium_horse_win logic, 0 or 1 | |
| 1. logic : | tianji_high_horse_win logic, 0 or 1 | |
| 2.0 : | number king wins, 0 to max 3 | random results |
| 1.0 : | number Tianji wins, 0 to max 3 | random results |
| 200.0 : | total winnings for Tianji silver dollars | random results |
Testcase 3, Change in Probabilty Rating on Horse Grades
| table 3 | printed in | tcl wiki format |
|---|---|---|
| quantity | value | comment, if any |
| 3: | testcase_number | |
| 50.0 : | high grade horse probability percent (a) , usually 50 | |
| 40.0 : | medium grade horse probability percent (b) , usually 35 | |
| 10.0 : | low grade horse probability percent (c) , usually 15 | |
| 200.0 : | Optional: Tianji bets on each heat (usually 200 silver dollars ): | |
| 3.0 : | answers: check sum all wins =? 3 : | |
| {heat_1 tl?kh win? 6.7 49.0 0. } { heat_2 tm?kl win? 17.6 6.3 1. } { heat_3 th?km win? 48.7 35.1 1. } : | list of horse race scores | |
| 0. logic : | tianji_low_horse_win logic, 0 or 1 | |
| 1. logic : | tianji_medium_horse_win logic, 0 or 1 | |
| 1. logic : | tianji_high_horse_win logic, 0 or 1 | |
| 1. : | number king wins, 0 to max 3 | random results |
| 2.0 : | number Tianji wins, 0 to max 3 | random results |
| 400.0 : | total winnings for Tianji silver dollars | random results |
Testcase 4, Classic Case of General Wins All 3 Races. Agrees with history, but no sure thing
| table 4 | printed in | tcl wiki format |
|---|---|---|
| quantity | value | comment, if any |
| 4: | testcase_number | |
| 50.0 : | high grade horse probability percent (a) , usually 50 | |
| 35.0 : | medium grade horse probability percent (b) , usually 35 | |
| 15.0 : | low grade horse probability percent (c) , usually 15 | |
| 200.0 : | Optional: Tianji bets on each heat (usually 200 silver dollars ): | |
| 3.0 : | answers: check sum all wins =? 3 : | |
| {heat_1 tl?kh win? 10.1 1. } { heat_2 tm?kl win? 31.1 13.8 1. } { heat_3 th?km win? 37.7 28.0 1. } : | list of horse race scores | |
| 1. logic : | tianji_low_horse_win logic, 0 or 1 | |
| 1. logic : | tianji_medium_horse_win logic, 0 or 1 | |
| 1. logic : | tianji_high_horse_win logic, 0 or 1 | |
| 0. : | number king wins, 0 to max 3 | random results |
| 3.0 : | number Tianji wins, 0 to max 3 | random results |
| 600.0 : | total winnings for Tianji silver dollars | random results |
Testcase 5, Rare Case of King Wins All 3 Races
| table 5 | printed in | tcl wiki format |
|---|---|---|
| quantity | value | comment, if any |
| 5: | testcase_number | |
| 50.0 : | high grade horse probability percent (a) , usually 50 | |
| 30.0 : | medium grade horse probability percent (b) , usually 35 | |
| 20.0 : | low grade horse probability percent (c) , usually 15 | |
| 200.0 : | Optional: Tianji bets on each heat (usually 200 silver dollars ): | |
| 3.0 : | answers: check sum all wins =? 3 : | |
| {heat_1 tl?kh win? 18.9 28.8 0. } { heat_2 tm?kl win? 13.1 18.7 0. } { heat_3 th?km win? 7.7 10.7 0. } : | list of horse race scores | |
| 0. logic : | tianji_low_horse_win logic, 0 or 1 | |
| 0. logic : | tianji_medium_horse_win logic, 0 or 1 | |
| 0. logic : | tianji_high_horse_win logic, 0 or 1 | |
| 3.0 : | number king wins, 0 to max 3 | random results |
| 0. : | number Tianji wins, 0 to max 3 | random results |
| 0.0 : | total winnings for Tianji silver dollars | random results |
Screenshots Section
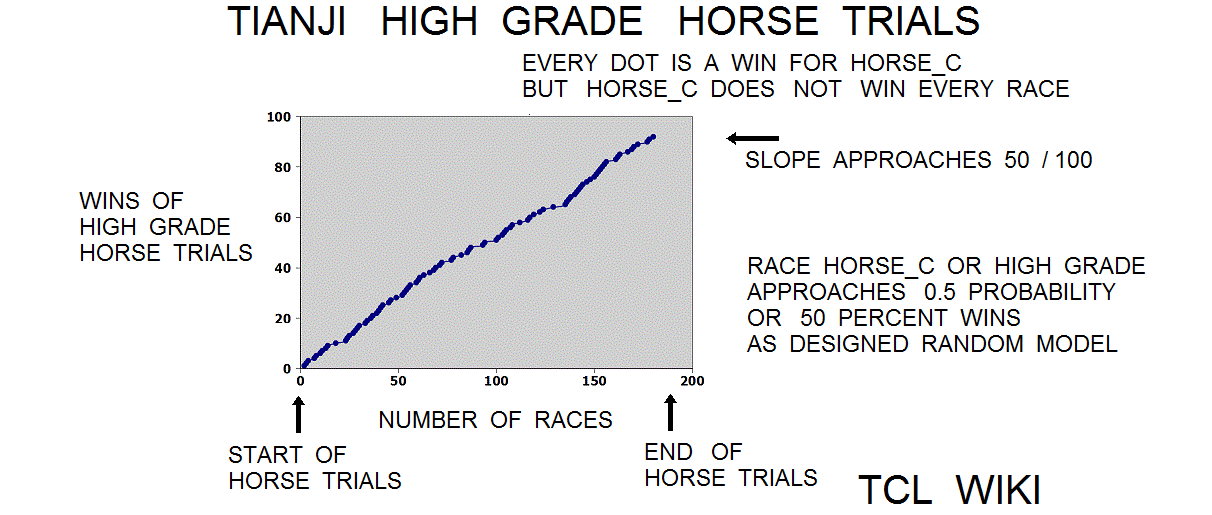
figure 1.
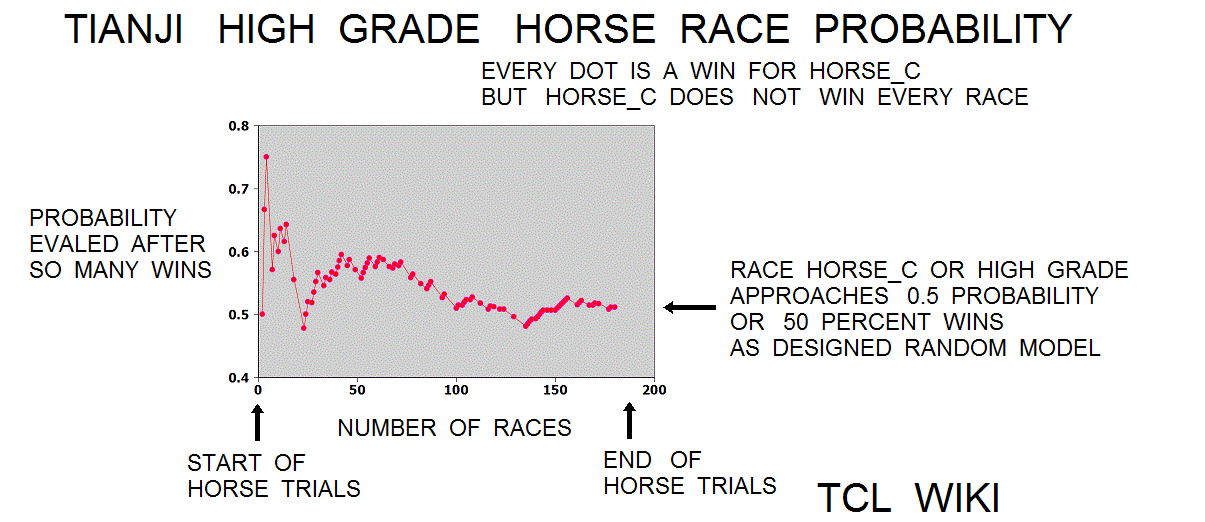
figure 2.
figure 3.
References:
- Horseracing in Tcl by RS
- Plugging a Math Gap with Harvard mathematician Shing-Tung Yau,
- Forbes Magazine 2007, Institute of Mathematical Sciences
- in Hong Kong studies betting on horse races and predicting the weather.
- Tian Ji , The Horse Racing, Peking University, Ying Fuchen,Xu Pengcheng,Xie Di, ACM Programmer's Contest
- The Ambitious Horse, Ancient Chinese Mathematics Problems, Lawence W. Swienciki, Ph.D.
- Game-theoreticanalysis of anancient Chinese horse race problem, Mingming Leng, Mahmut Parlar,
- DeGroote School of Business, McMaster University, Hamilton, Ont., Canada L8S 4M4
- 10 December 2004
- Random Walk Equation Slot Calculator Example
- Plugging a Math Gap with Harvard mathematician Shing-Tung Yau, Forbes Magazine 2007,
- Institute of Mathematical Sciences
- in Hong Kong studies betting on horse races and predicting the weather
- Sumerian Construction Rates and eTCL Slot Calculator Demo Example
- Chabert, J. "Methods of False Position." Ch. 3 in A History of Algorithms: From the Pebble to the Microchip. , 1999.
- John Hannah , False position in Leonardo of Pisa's Liber Abbaci,Historia Mathematica Volume 34 issue 3 2007
- Eugene C. Boman,False Position, Double False Position and Cramer's Rule, College Mathematics Journal
- Howard Eves ,On the practicality of the rule of false position, Mathematics Teacher Volume 51
- Joy B. Easton, the rule of double false position, Mathematics Teacher Volume 60
- Vera Sanford, the rule of false position, Mathematics Teacher Volume 44 issue 5 1951
- Karine Chemla, Reflections on the World-wide History of the Rule of False Double Position, or: How a Loop Was Closed
- Thomas G. Edwards -- Using the Ancient Method of False Position to Find Solutions, Mathematics Teaching in the Middle School Volume 14 issue 4 2008
- Oneliner's Pie in the Sky
- One Liners
- Category Algorithm
- Babylonian Number Series and eTCL demo example calculator
- Brahmagupta Area of Cyclic Quadrilateral and eTCL demo example calculator
- Gauss Approximate Number of Primes and eTCL demo example calculator
- Taking a Weighted Average, Dr Math, mathforum.org/dr.math, dated 03/20/2003
- google <Weighted Average, Dr Math>, mathforum.org/dr.math
- Using Weighted Criteria to Make Decisions, Dr Math>, mathforum.org/dr.math, dated 07/18/2008
- google <Weighted sum product model Decision >
- harmonic mean discussed in Additional math functions
- harmonic mean discussed in Tcl Normalized Extended Benchmarks
- see arithmetic mean on tcl-wiki Stats 2011-05-22, RLE
- see similar 1/(1/nth) terms method used in
- Babylonian Combined Market Rates and eTCL demo example calculator, numerical analysis
- Zhang Baichun and Jürgen Renn (eds.) , Transformation and Transmission:
- Chinese Mechanical Knowledge and the Jesuit Intervention
- Joint Research Group of the MPIWG and its Partner Group at the IHNS of the CAS.
- Probability models on horse-race outcomes,
- MUKHTAR M. ALI, Department of Economics, University of Kentucky, USA
- Probability and Optimization Probability and Optimization Models for Racing Horse Models,
- Victor S. Y. Lo University of British Columbia University of British Columbia, Fidelity Investments
- Designing competitions between teams of individuals, Pingzhong Tanga,Yoav Shohamb,c, Fangzhen Lina,
- Mentions ACM horse race problems relative to teams of computer students.
- Sun Bin: Distinguished Military Strategist After Sun Zi, By David Wu, Epoch Times
- Lecture 4: Matching Algorithms for Bipartite Graphs
- Professor: Clifford Stein
- Lecture notes on bipartite matching
- 100: “Matchings” Fall 2012
- Matching (graph theory) From Wikipedia, the free encyclopedia
- Bayes Theorem,Bayes Theorem in short is a method of analysing data.
- Massachusetts Institute of Technology Handout 3
- Combinatorial Optimization February 9th, 2009 Michel X. Goemans
- Paper mentions Tianji horse race problem.
- Designing competitions between teams of individuals,
- Pingzhong Tanga, Yoav Shohamb, Fangzhen Lin,
- Department of Computer Science, Hong Kong University of Science and Technology,
- Clear Water Bay, Hong Kong
- Computer Science Department, Stanford University, CA 94305, United States
- Microsoft Israel R&D Center, Herzliya, Israel.
- Quanta mag article. How Ancient War Trickery Is Alive in Math Today
Appendix Code
appendix TCL programs and scripts
# pretty print from autoindent and ased editor
# General Tianji' Chinese Horse Race Strategy Calculator
# written on Windows XP on eTCL
# working under TCL version 8.5.6 and 1.0.1
# gold on TCL WIKI, 25feb2017
package require Tk
package require math::numtheory
namespace path {::tcl::mathop ::tcl::mathfunc math::numtheory }
set tcl_precision 17
frame .frame -relief flat -bg aquamarine4
pack .frame -side top -fill y -anchor center
set names {{} { high grade horse probability percent (a) , usually 50 :} }
lappend names { medium grade horse probability percent (b) , usually 35:}
lappend names { low grade horse probability percent (c) , usually 15: }
lappend names { optional: : }
lappend names { answers: check sum all wins =? 3 }
lappend names { number of King wins, 0 to max 3 }
lappend names { number of Tianji wins, 0 to max 3 : }
lappend names { total winnings for Tianji silver dollars :}
foreach i {1 2 3 4 5 6 7 8} {
label .frame.label$i -text [lindex $names $i] -anchor e
entry .frame.entry$i -width 35 -textvariable side$i
grid .frame.label$i .frame.entry$i -sticky ew -pady 2 -padx 1 }
proc about {} {
set msg "Calculator for General Tianji's Chinese Horse Race Strategy
from TCL WIKI,
written on eTCL "
tk_messageBox -title "About" -message $msg }
proc tianji_horse_race { xxx1 } {
global side1 side2 side3 side4 side5
global side6 side7 side8
set high_grade_prob 50.
set medium_grade_prob 35.
set low_grade_prob 15.
set tianji_winnings 0.
set king_winnings 0.
# normal 15 percent = low_grade_prob
# normal 35 percent = medium_grade_prob
# normal 50 percent = high_grade_prob
set high_grade_prob $side1
set medium_grade_prob $side2
set low_grade_prob $side3
set tianji_low [expr $low_grade_prob * [expr { rand() } ] ]
set king_high [expr $high_grade_prob * [expr { rand() } ] ]
set tianji_low 1.0
set tianji_medium 1.0
set tianji_high 1.0
set king_low 1.0
set king_medium 1.0
set king_high 1.0
set check_sum 0.0
# 15 percent = low_grade
# 35 percent = medium_grade
# 50 percent = high_grade
set tianji_low [expr $low_grade_prob * [expr { rand() } ] ]
set king_high [expr $high_grade_prob * [expr { rand() } ] ]
if { [max $tianji_low $king_high ] == $tianji_low } { set tianji_winnings 1. }
if { [max $tianji_low $king_high ] == $king_high } { set king_winnings 1. }
set tianji_medium [expr $medium_grade_prob * [expr { rand() } ] ]
set king_low [expr $low_grade_prob * [expr { rand() } ] ]
if { [max $tianji_medium $king_low ] == $tianji_medium } { set tianji_winnings [+ $tianji_winnings 1.] }
if { [max $tianji_medium $king_low ] == $king_low } { set king_winnings [+ $king_winnings 1. ] }
set tianji_high [expr $high_grade_prob * [expr { rand() } ] ]
set king_medium [expr $medium_grade_prob * [expr { rand() } ] ]
if { [max $tianji_high $king_medium ] == $tianji_high } { set tianji_winnings [+ $tianji_winnings 1.] }
if { [max $tianji_high $king_medium ] == $king_medium } { set king_winnings [+ $king_winnings 1. ] }
set check_sum [+ $king_winnings $tianji_winnings ]
set side5 $check_sum
set side6 $king_winnings
return $tianji_winnings }
proc calculate { } {
global answer2
global side1 side2 side3 side4 side5
global side6 side7 side8
global testcase_number
incr testcase_number
set side1 [* $side1 1. ]
set side2 [* $side2 1. ]
set side3 [* $side3 1. ]
set side4 [* $side4 1. ]
set side5 [* $side5 1. ]
set side6 [* $side6 1. ]
set side7 [* $side7 1. ]
set side8 [* $side8 1. ]
# initialize placeholder answer
set answer2 [tianji_horse_race 3 ]
set side7 $answer2
set side8 [* 200. $answer2 ]
}
proc fillup {aa bb cc dd ee ff gg hh} {
.frame.entry1 insert 0 "$aa"
.frame.entry2 insert 0 "$bb"
.frame.entry3 insert 0 "$cc"
.frame.entry4 insert 0 "$dd"
.frame.entry5 insert 0 "$ee"
.frame.entry6 insert 0 "$ff"
.frame.entry7 insert 0 "$gg"
.frame.entry8 insert 0 "$hh"
}
proc clearx {} {
foreach i {1 2 3 4 5 6 7 8 } {
.frame.entry$i delete 0 end } }
proc reportx {} {
global side1 side2 side3 side4 side5
global side6 side7 side8
global testcase_number
console show;
puts "%|table $testcase_number|printed in| tcl wiki format|% "
puts "&| quantity| value| comment, if any|& "
puts "&| $testcase_number:|testcase_number | |& "
puts "&| $side1 :|high grade horse probability percent (a) , usually 50 | |&"
puts "&| $side2 :|medium grade horse probability percent (b) , usually 35 | |& "
puts "&| $side3 :|low grade horse probability percent (c) , usually 15 | |& "
puts "&| $side4 :|optional:| |&"
puts "&| $side5 :|answers: check sum all wins =? 3 : | |& "
puts "&| $side6 :|number king wins, 0 to max 3 | random results |& "
puts "&| $side7 :|number Tianji wins, 0 to max 3 | random results |& "
puts "&| $side8 :|total winnings for Tianji silver dollars | random results |&"
}
frame .buttons -bg aquamarine4
::ttk::button .calculator -text "Solve" -command { calculate }
::ttk::button .test2 -text "Testcase1" -command {clearx;fillup 50. 35. 15. 1.0 0. 0. 0. 0.}
::ttk::button .test3 -text "Testcase2" -command {clearx;fillup 50. 30. 20. 1.0 0. 0. 0. 0. }
::ttk::button .test4 -text "Testcase3" -command {clearx;fillup 50. 40. 10. 1.0 0. 0. 0. 0. }
::ttk::button .clearallx -text clear -command {clearx }
::ttk::button .about -text about -command {about}
::ttk::button .cons -text report -command { reportx }
::ttk::button .exit -text exit -command {exit}
pack .calculator -in .buttons -side top -padx 10 -pady 5
pack .clearallx .cons .about .exit .test4 .test3 .test2 -side bottom -in .buttons
grid .frame .buttons -sticky ns -pady {0 10}
. configure -background aquamarine4 -highlightcolor brown -relief raised -border 30
wm title . "General Tianji' Chinese Horse Race Strategy Calculator"
# end of deck Pushbutton Operation
For the push buttons, the recommended procedure is push testcase and fill frame, change first three entries etc, push solve, and then push report. Report allows copy and paste from console.
For testcases in a computer session, the eTCL calculator increments a new testcase number internally, eg. TC(1), TC(2) , TC(3) , TC(N). The testcase number is internal to the calculator and will not be printed until the report button is pushed for the current result numbers. The current result numbers will be cleared on the next solve button. The command { calculate; reportx } or { calculate ; reportx; clearx } can be added or changed to report automatically. Another wrinkle would be to print out the current text, delimiters, and numbers in a TCL wiki style table as
puts " %| testcase $testcase_number | value| units |comment |%" puts " &| volume| $volume| cubic meters |based on length $side1 and width $side2 |&"
Console program for race output as CVS spreadsheet, includes > equal probability horses <
# pretty print from autoindent and ased editor
# initial console program, Chinese horse race problem
# comma delimited spreadsheet for number of horse races
# written on Windows XP on eTCL
# working under TCL version 8.5.6 and eTCL 1.0.1
# gold on TCL WIKI, 10feb2017
package require Tk
package require math::numtheory
namespace path {::tcl::mathop ::tcl::mathfunc math::numtheory }
set tcl_precision 17
console show
set i 2000
set horse_race_days 1
puts "horse race number , trial heat, winner, wins of particular horse, cum. probability, loser,loser, horse_a , horse_b , horse_c , last place "
while {$i>0} {
if { $horse_race_days > 180 } { break }
set horse_a [ expr { rand() } ]
set horse_b [ expr { rand() } ]
set horse_c [ expr { rand() } ]
set trial [ expr { rand() } ]
if { $trial > 0 && $trial < .2 } { set winner_name "horse_a" ; set loser_name "horse_b,horse_c" }
if { $trial > .2 && $trial < .5 } { set winner_name "horse_b" ; set loser_name "horse_a,horse_c" }
if { $trial > .5 && $trial < 1. } { set winner_name "horse_c" ; set loser_name "horse_a,horse_b" }
set winner [max $horse_a $horse_b $horse_c]
set last [min $horse_a $horse_b $horse_c]
lappend winner_list $winner_name
lappend loser_list $loser_name
#set number_wins [ lsearch -all $winner_list $winner_name ]
set ee [ llength $winner_list ]
set kk [ llength [ lsearch -all $winner_list $winner_name ] ]
set prob [ expr { ($kk*1.) / $ee } ]
if {$winner_name == "horse_c" } {
puts "$horse_race_days ,$trial ,$winner_name,$kk,$prob,$loser_name,$trial, $winner, $horse_a , $horse_b , $horse_c , $last "}
incr horse_race_days
incr i -1
}
#end of deckcvs output for > wins only < of horse_c
horse race number , trial heat, winner, wins of particular horse, cum. probability, loser,loser, horse_a , horse_b , horse_c , last place 2 ,0.72403450297379612 ,horse_c,1,0.5,horse_a,horse_b,0.72403450297379612, 0.86678423540051297, 0.13588783151278638 , 0.86678423540051297 , 0.042644376420716001 , 0.042644376420716001 3 ,0.87722261151169545 ,horse_c,2,0.66666666666666663,horse_a,horse_b,0.87722261151169545, 0.84789148059109765, 0.84789148059109765 , 0.51211429457744317 , 0.104948963087494 , 0.104948963087494 4 ,0.86264225927304583 ,horse_c,3,0.75,horse_a,horse_b,0.86264225927304583, 0.61519644810594454, 0.48043167706599071 , 0.61519644810594454 , 0.60670331660970267 , 0.48043167706599071 7 ,0.73498046013292873 ,horse_c,4,0.5714285714285714,horse_a,horse_b,0.73498046013292873, 0.27436126688232704, 0.27436126688232704 , 0.18981249127062619 , 0.17854078541441856 , 0.17854078541441856 8 ,0.96185003824618176 ,horse_c,5,0.625,horse_a,horse_b,0.96185003824618176, 0.81659345413399553, 0.81659345413399553 , 0.48618363006328402 , 0.28827047361446101 , 0.28827047361446101 10 ,0.76152973378148381 ,horse_c,6,0.59999999999999998,horse_a,horse_b,0.76152973378148381, 0.95698579864436095, 0.078298148735565204 , 0.95698579864436095 , 0.060317815775199707 , 0.060317815775199707
Console program for tianji horse race and combined unequal probability
# pretty print from autoindent and ased editor
# subroutine for tianji horse race and combined unequal probability
# working under TCL version 8.5.6 and eTCL 1.0.1
# console program written on Windows XP on eTCL
# written on Windows XP on eTCL
# working under TCL version 8.5.6 and eTCL 1.0.1
# gold on TCL WIKI, 2mar2017
package require Tk
package require math::numtheory
namespace path {::tcl::mathop ::tcl::mathfunc math::numtheory }
set tcl_precision 17
console show
proc tianji_horse_race { xxx1 } {
set i 2000
set horse_race 1
set trial 1.
set trialx 1.
set tianji_low 1.
set tianji_middle 1.
set tianji_high 1.
set king_low 1.
set king_middle 1.
set king_high 1.
set program_result {}
set winner_list1 {}
set winner_list2 {}
while {$i>0} {
if { $horse_race > 10 } { break }
set trial [ expr { rand() } ]
set counter 1
set tianji_low [expr 15.* [expr { rand() } ] ]
set king_high [expr 50.* [expr { rand() } ] ]
# 15 percent = low_grade
# 35 percent = medium_grade
# 50 percent = high_grade
if { [max $tianji_low $king_high ] == $tianji_low } { lappend winner_list2 " horse_race$horse_race heat$counter " tianji_low }
if { [max $tianji_low $king_high ] == $king_high } { lappend winner_list2 " horse_race$horse_race heat$counter " king_high }
incr counter
set tianji_middle [expr 35.* [expr { rand() } ] ]
set king_low [expr 15.* [expr { rand() } ] ]
if { [max $tianji_middle $king_low ] == $tianji_middle } { lappend winner_list2 " horse_race$horse_race heat$counter " tianji_middle }
if { [max $tianji_middle $king_low ] == $king_low } { lappend winner_list2 " horse_race$horse_race heat$counter " king_low }
incr counter
set tianji_high [expr 50.* [expr { rand() } ] ]
set king_middle [expr 35.* [expr { rand() } ] ]
if { [max $tianji_high $king_middle ] == $tianji_high } { lappend winner_list2 " horse_race$horse_race heat$counter " tianji_high \n}
if { [max $tianji_high $king_middle ] == $king_middle } { lappend winner_list2 " horse_race$horse_race heat$counter " king_middle \n }
incr horse_race
incr i -1
}
return $winner_list2 }
set program_result [ tianji_horse_race 3 ]
puts " list of winners = \n $program_result "
#end of deckoutput follows for list of winners in trial races with three 3 heats, > unequal probability horses <
list of winners =
{ horse_race1 heat1 } king_high { horse_race1 heat2 } tianji_middle { horse_race1 heat3 } tianji_high {
} { horse_race2 heat1 } king_high { horse_race2 heat2 } king_low { horse_race2 heat3 } king_middle {
} { horse_race3 heat1 } tianji_low { horse_race3 heat2 } tianji_middle { horse_race3 heat3 } tianji_high {
} { horse_race4 heat1 } king_high { horse_race4 heat2 } tianji_middle { horse_race4 heat3 } tianji_high {
} { horse_race5 heat1 } king_high { horse_race5 heat2 } tianji_middle { horse_race5 heat3 } tianji_high {
} { horse_race6 heat1 } king_high { horse_race6 heat2 } tianji_middle { horse_race6 heat3 } tianji_high {
} { horse_race7 heat1 } king_high { horse_race7 heat2 } king_low { horse_race7 heat3 } tianji_high {
} { horse_race8 heat1 } tianji_low { horse_race8 heat2 } tianji_middle { horse_race8 heat3 } tianji_high {
} { horse_race9 heat1 } king_high { horse_race9 heat2 } king_low { horse_race9 heat3 } king_middle {
} { horse_race10 heat1 } king_high { horse_race10 heat2 } tianji_middle { horse_race10 heat3 } king_middle {
} Example eTCL code for selecting winners for random horses in a race
# random horses in a race
set horse_a [ expr { rand() } ]
set horse_b [ expr { rand() } ]
set horse_c [ expr { rand() } ]
set trial [ expr { rand() } ]
if { $trial > 0 && $trial < .2 } { set winner_name "horse_a" ; set loser_name "horse_b,horse_c" }
if { $trial > .2 && $trial < .5 } { set winner_name "horse_b" ; set loser_name "horse_a,horse_c" }
if { $trial > .5 && $trial < 1. } { set winner_name "horse_c" ; set loser_name "horse_a,horse_b" }
set winner [max $horse_a $horse_b $horse_c]Example eTCL code for horse accidents or shortfalls
if { [ expr { rand() } ] <= .15 } {set hoof_infection_this_year 1 }
set race_meters_shortfall [ expr { $meters*.1*rand() } ]
set race_meters_shortfall [ expr { int($race_meters_shortfall ) } ]
(...many...)
set total_meters [ expr { $meters - $race_meters_shortfall*.1*$hoof_infection_this_year
# or decrement speed of horse if more effective in program
set total_meters_speed [ expr { $normal_meters_speed - $race_speed_shortfall*.1*$hoof_infection_this_year
set total_meters_speed_exponent [ expr { $normal_meters_speed_exponent*.1*$hoof_infection_this_yeargold10Dec2018. This page is copyrighted under the TCL/TK license terms, this license .
Comments Section
Please place any comments here with your wiki MONIKER and date. Thanks. gold 10Dec2018
| Category Numerical Analysis | Category Toys | Category Calculator | Category Mathematics | Category Example | Toys and Games | Category Games | Category Application | Category GUI |