Playing Recursion V2 >> demo examples for one liner programs
Playing Recursion V2 >> demo examples for one liners programs
This page is under development. Constructive comments are welcome, but please load any constructive comments in the comments section at the bottom of the page. Please include your wiki MONIKER and date in your comment with the same courtesy that I will give you. Aside from your courtesy, your wiki MONIKER and date as a signature and minimal good faith of any Internet post are the rules of this Tcl-WIKI. Its very hard to reply reasonably without some background of the correspondent on his WIKI bio page. Thanks, gold 6/8/2021 update.
- Playing Recursion V2 >> demo examples for one liners programs
- Pseudocode Section
- Console Session from Namespace ::liner
- if, if, and iffy Table
- McCarthy Symbolic Logic Table
- Table for List of Recursion Procs and Funcs
- Screenshots Section
- Figure 1. Playing Recursion Screenshot 1
- Figure 2. Playing Recursion Screenshot Two
- Figure 3. Playing Recursion Screenshot Three
- Figure 4. Playing Recursion V2 triangle function
- Figure 5. Playing Recursion V2 step function
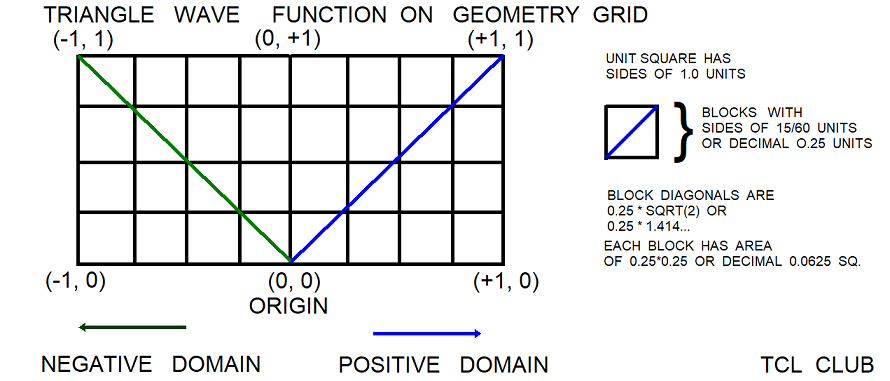
- Figure 6. Playing Recursion V2 triangle wave function
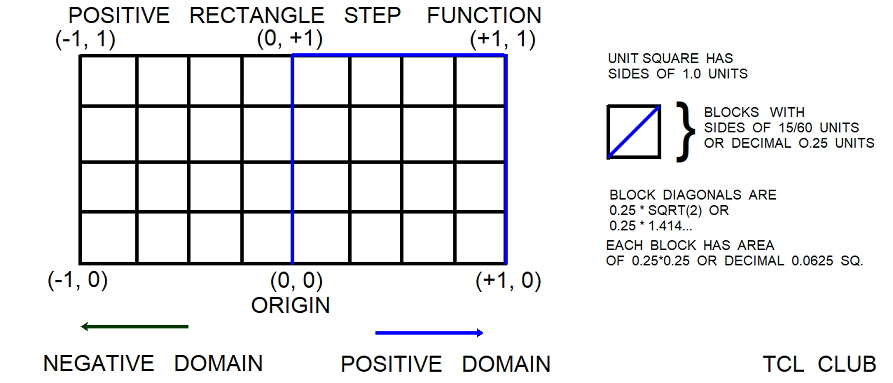
- Figure 7. Playing Recursion V2 positive step function
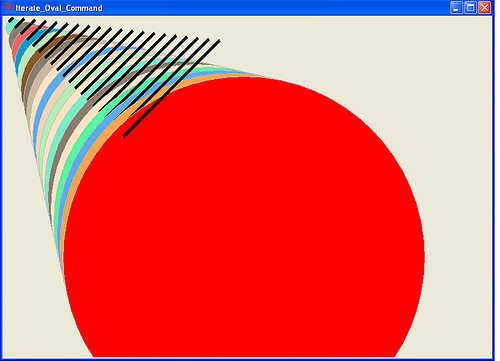
- Figure 8. Iteration on Canvas
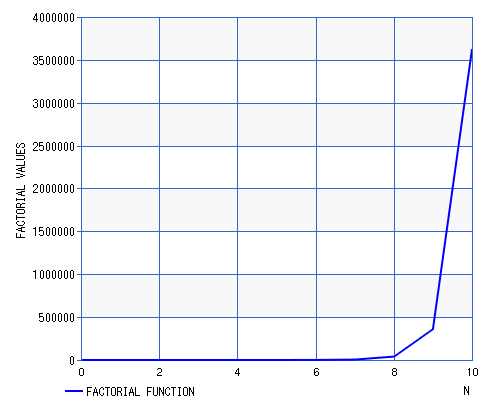
- Figure 9. Factorial Function N!
- Testcases Section
- Testcase 4, One Liner Programs Approach to the Fibonaci series
- Testcase 5, One Liners Programs Approach to the Golden Section
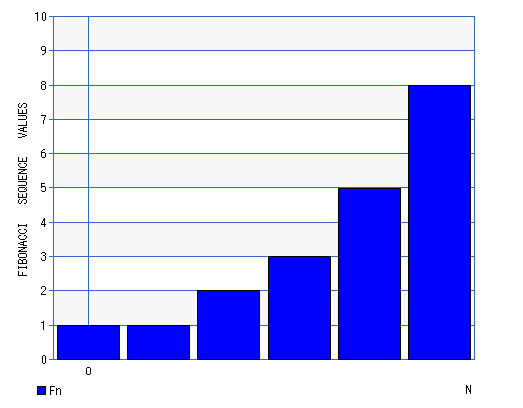
- Figure 10. Fibonaci small numbers
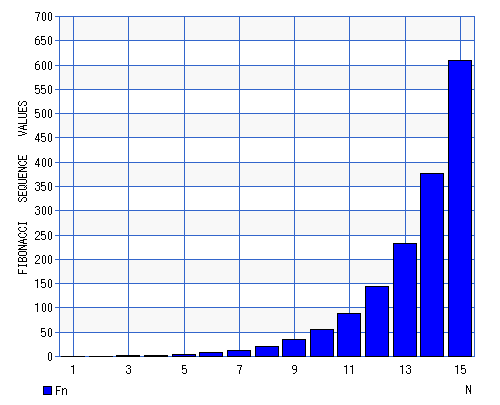
- Figure 11. Fibonaci large numbers
- Testcase 6, One Liners Programs Approach to the Approximate Pie
- testing recursion on infinite series pi = 4* atan(fib(2*$n+1)], 1 < f($n) terms < $n
- Figure 12. minimal polynomial x**2 − x − 1
- Figure 13. Unit Circle
- Figure 14. Circle with radius of phi
- Figure 15. MACHIN PI 2 TERM FORMULA ed2
- Testcase 7, Polynomials, Sum of Integers, Sum of Squares, Sum of Cubes, and Sum of Nth Powers
- Testcase 8, Triangular Number Multiplication
- References
- References on Golden Ratio and pi Math
- Appendix Code
- Hidden Comments Section
Preface
gold 2020-10-08: Here is some source code to supplement the TCL Wiki page Playing with Recursion by RS. This supplemental code is intended for study of McCarthy theorems on computer arithmetic into one-line programs.
Introduction
Playing with Recursion by RS translates the McCarthy theorems into one-line Tcl scripts. To further qualify, some of the one-line programs require additional helper functions. With supplemental code and extensions to the original code, the "easy eye" console was used as a testbed for one-line programs in ActiveTcl on Windows 10. Using the easy eye testbed, the code in Playing with Recursion was extended with a few more functions. The "Easy Eye" console testbed has large black type on green background for bad eyes. The "easy eye" console testbed includes an extra Self_Help button under the normal Help button of ActiveTcl console display. This "easy eye" console testbed was written on Windows10 Console in ActiveTCL and has dependencies on same. The dependency of the "easy eye" console testbed on the ActiveState TCL and Windows10 Console TK widget is noted on the page introduction and source code. I believe that the proposed implementation of some TCL examples below in the Tcllib will accommodate both the Windows10 and UNIX users of TCL.
The development of programming languages and techniques has been influenced by the work of researchers such as John McCarthy and others who have contributed to our understanding of the mathematical theory of computation. The use of McCarthy's notation for the mathematical theory of computation is a valuable tool for developing algorithms and systems that can handle complex and challenging problems. Overall, the ongoing exploration of new programming techniques and approaches is a critical aspect of the scientific and technological landscape. The insights gained through this research will continue to inspire and inform future generations of scientists and inventors, and will help to shape the course of our technological progress for years to come.
Not a Replacement for TCL Core
This page on developing pseudocode examples and one line procedures is not a replacement for the current Tcl core and Tcllib, which is much improved since Tcl version 4, and other <faster> language constructs. math ops, Tcllib routines, and other compiled routines can reduce the cost of big-data tasks by about 1/3. The time savings of the core are not always obvious on small quantities of data, like 4 or 5 numbers. Performance of one-line programs may suffer degradation due to lengthy recursion calls, and may be limited by constraints on recursion. Dependence on math operator notation, helper procedures, math check examples, degradation due to lengthy recursion calls, and special library functions should be noted in the comment lines.
Discussion
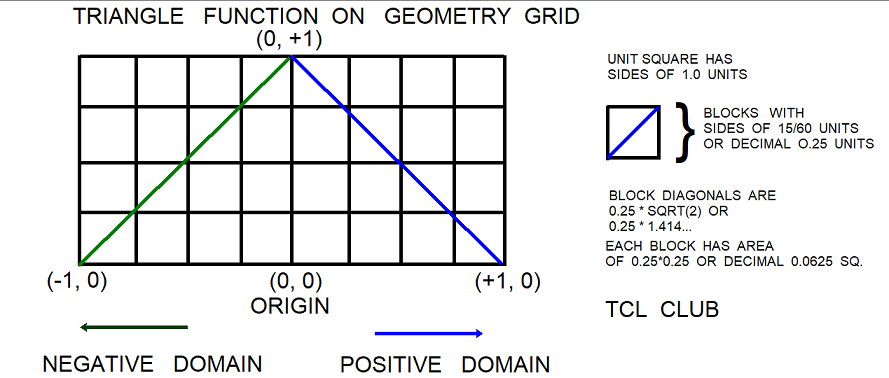
Professor McCarthy advocates "conditional expressions", where a conditional expression is a sequence alternating condition and result clauses. Each condition may represent one or more domains on the number line. In Tcl, the condition is a domain defined by if or the ? in a?b:c operator of expr. In Playing with Recursion, the conditional was mostly ?. The result, or estimated variable function f(v), is sort of hovering and ambiguous cloud of values over the condition domain. For the triangle function, the condition domains are:
- $variable < 0
- $variable = 0
- 0 < $variable < 1
- $variable > 1
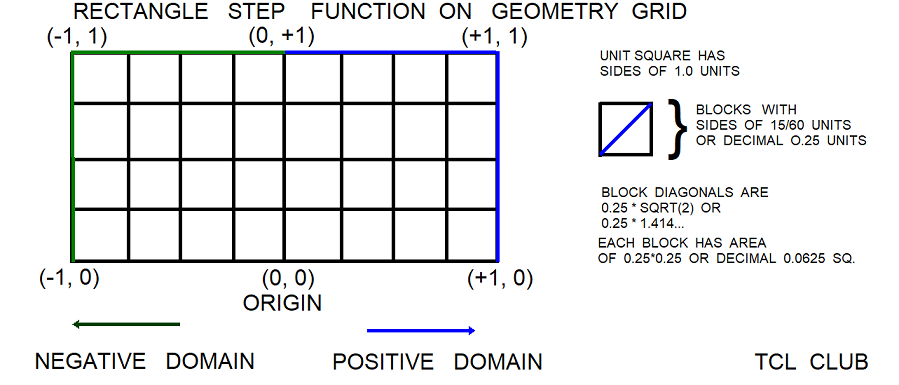
However, since the Playing with Recursion is concerned primarily with positive integer arithmetic, the number of condition domains may be abbreviated, merged, or constrained to the positive domain only. As another example for the rectangle step function, the condition domains might be:
- $variable < -1
- -1 < $variable < 0
- $variable = 0
- 0 < $variable < 1
- $variable > 1
Yet another example is the triangle wave function centered at the origin. After the algorithm using "conditional expressions" was developed and "rigorously proved" though known functions, parts of the recursion algorithm could possibly be sped up with equivalent methods of iteration, mapping tables, or executing compiled rather than interpreted code.
Not a Replacement for TCL Core
This page on developing McCarthy based algorithms is not a replacement for the current Tcl core and Tcllib, which is much improved since Tcl version 4, and other <faster> language constructs. math ops, Tcllib routines, and other compiled routines can reduce the cost of big-data tasks by about 1/3. The time savings are not always obvious on small quantities of data. Performance of one-line programs may suffer degradation due to lengthy recursion calls, and may be limited by constraints on recursion. Dependence on math operator notation, helper procedures, math check examples, degradation due to lengthy recursion calls, and special library functions should be noted in the comment lines.
Added Functions
Some functions were added in the Easy Eye testbed. Factorial recursion quickly exceeds domain. fac is limited by recursion constraints, and excessive time delay beyond factorial 4. Functions min and max are basic integer functions, but may need some error checks for entry zeros and equality, $m == $n. Logic tested for <= as puts {< 5 0} returns 0, puts {<= 0 5} returns 1, and puts {<= 10 10} returns 1. Logic tested for func < as puts {< 5 0} returns 0 and puts {< 0 5} returns 1. Swap brackets for {}. zero_killer replaces 0 with 0.0000001 to avoid division by zero. It proved useful for observed data loaded from Tcl programs into spreadsheet calculation charts. An RS proc with the x?y:z operator seemed a good model in regular Tcl as proc sgn5 x {set temp [expr {$x>0? 1 : $x<0? -1 : 0}]}. In the Playing_Recursion code, the proc sgn5 seemed to work well as func sgn5 n { [expr {$n>0? 1 : $n<0? -1 : 0}]}. But when [> $n 0 ]? and [< $n 0 ]? was substituted, could not get the func sgn5 to work. The most understandable RS derived code was proc sgn7 nn { if {$nn>0} { return 1 } elseif {$nn<0} { return -1 } else { return 0 }}. The timimg was time { sgn7 7 } 5000 , which returned 0.4554 microseconds per iteration. I have to say that McCarthy and RS have a different take on setting up the algorithms as <conditional regions> of variable space, which seems to apply well to regular Tcl coding.
Naughty Nots in Knots
In the original set of Playing with Recursion, there was the positive equal, proc eq {m n} {string equal $m $n} ;# RS. What was intriguing is that the proc eq works on strings as well as integers. This proc eq is very fast at 0.65 microseconds delay and does not rely on expr or math. It seemed desirable to have an equally fast not equal or ne. Most of the algorithm textbooks and McCarthy papers assume 6 comparison operators are available. For example, Fortran 77 has logic operators EQ,NE,LT,LE,GT, and GE as well as 3 relational operators AND,OR, and NOT. Qbasic has Operator Relation Expressions as = Equality, <> not equal , > Greater than, < Less than, >= Greater Than or Equal, and <= Less than. For Qbasic, the logical operators are NOT, AND, XOR, NOR, or EQV. Several variants of ne were loaded and tested in the Playing Recursion testbed for performance and speed.
gold 2/26/2024 update. Gist. In the original Playing with Recursion set, there was a positive equal function, proc eq, that checked for equality between two values, m and n. This function worked on both strings and integers, was very fast with a delay of 0.65 microseconds, and did not rely on expr or math. The goal was to create an equally fast not equal or ne function.
# testing negative logic for =! and ne
# procs =! and ne work on strings too
proc =! {m n} { if {[string equal $m $n]} then {return 0} else {return 1} }
# Usage liner::=! 5 5 r> 0, liner::=! 5 6 r> 1
# Usage time {liner::=! 5 5 } 5 returns 8.6 microseconds per iteration
proc ne {m n} { abs [string compare $m $n]}
# Usage liner::ne 5 5 r> 0, liner::ne 5 6 r> 1
time {liner::ne 5 5 } 5 returns 12.6 microseconds per iteration
proc fie {m n} { abs [string compare $m $n]}
time {fie b b } 5 ;# returns 1.6 microseconds per iteration
proc fibber {m n} { if {[string equal $m $n]} {return 0} {return 1} }
# fibber works on strings but slow
time {fibber b b } 5 ;# returns 8.0 microseconds per iteration
# gold standard proc for eq in global space
# liner::= is same proc in namespace liner::
proc eq {m n} {string equal $m $n} ;# RS
time {eq 1 1 } 1000 returns 0.608 microseconds per iteration in global space
time { liner::= 1 1} 1000 returns 0.436 microseconds per iteration in namespace ::linerPlaying Recursion V2 in a Namespace
One can load the the bulk of Playing Recursion V2 into a namespace called ::liner. The advantage of the namespace ::liner is that Playing Recursion is no longer overwriting the math commands for +,-,*, and others in the global space of the TCL script. In the global side of the testbed, one can write regular TCL procs that either call the global math commands in the TCL core and Tcllib library or else call the func commands in the ::liner namespace. Somewhat like the expr command, the func commands in the ::liner::Playing_Recursion namespace have their own set of rules, logic, and a limited set of commands that may conflict with the different set of commands in the global namespace. So a typical console session in the Playing Recursion testbed might have the entire command set of global commands, the limited ::liner::Playing_Recursion set of namespace commands, and the temporary Playing_Recursion funcs and procs under test. The command to invoke the lists of functions inside namespace would be ::liner::* and the command for the demo would be ::liner::demo. The original func command of RS in installed inside the namespace, so ::liner::func would be used to create a new func inside the namespace ::liner::. The available commands, procs, and funcs in the namespace are listed with info commands ::liner::* While good for studying the McCarthy algorithm math theorems, the Playing_Recursion funcs are recursion limited with lengthy return times compared to the precompiled core in the TCL core. So it is suspected that the testbed session on the console would have to develop a McCarthy based algorithm in ::liner::Playing_Recursion and then transfer the algorithm into the regular TCL commands in the global namespace.
Some algorithm examples petitioned in ticket to Tcclib
gold 10/5/2021 updated. From some of the algorithm examples below, I have petitioned a ticket to Tcclib, figurate numbers and sums of powers. The ticket is f8adb7a036 2021-09-18 08:29:50, Patch Open math figurate numbers and sums of powers. From the algorithm testing recorded below, some of the figurate functions developed inside the namespace liner:: are running into recursion limits. For example, the function liner::square has lengthy recursion and too many nested evaluations beyond 30. The liner::cube has lengthy recursion and too many nested evaluations beyond 10. The Glaisher formula returns the triangular multiplication product TNX as an integer from two positive natural numbers. The test algorithm liner::trix 30 5 -> 150 is working, but too many nested evals beyond m equals 30.
gold 10/5/2021 updated. Examples for procs IsEven, IsOdd, IsNegative, and IsPositive have been added to Ticket E035b93f36, Collatz_sequences And Modified Collatz_sequences. These one liner procs for logic were based on IsPrime by RS and others on this TCL Wiki, using the expr logic feature. These are logic procs that are effectively segmenting or bisecting the infinite numberline using the McCarthy based algorithms in his paper. I suppose IsZero and IsNotZero might be useful logic also in some situations.
proc IsOdd { N } { return [ expr {$N % 2} ] }
proc IsEven { N } { return [ expr { ( $N + 1 ) % 2} ] }
proc IsNegative { x } { return [ expr {$x<0}]}
proc IsPositive { x } {return [ expr {$x>0}]}gold 10/5/2021 updated. I have installed the TCL recursion deck inside the namespace liner, so I can invoke recursion math functions without conflicts to the regular TCL functions in the TCL core. I am not that familiar with the use of namespaces. This TCL deck has gotten to be one tricky set of code, if one inadvertently drops a critical bracket or omits critical spaces. The numerous examples on this wiki page include code lines that might be incompatible, inefficient, recursion limited, dead_weights, or redundant if installed in the same program. The main point of the deck is that one can develop a TCL subroutine or algorithm using the McCarty theorems inside the namespace liner::. Once the subroutine is working inside the namespace, one can either translate from McCarthy recursion functions or otherwise continue the development outside the namespace in the TCL core. One alternative might be to load the namespace liner into the local copy of Tcllib with some pointers. This TCL recursion deck was written in Windows10 Console in ActiveTCL and has dependencies on same. Note: Namespace liner:: has to have mathop and mathfunc installed for some functions and procs to work inside the namespace.
Conclusions
Professor McCarthy and RS have a different take on setting up the algorithms as <conditional regions> of variable space, which seems to apply well to regular Tcl coding. McCarthy developed his own notation for the mathematical theory of computation in several papers. And later, McCarthy applied much of his mathematical theory of computation to the development of the Lisp computer language.
There are pros and cons to one-line programs. Working with recursion, primes, and timing the procedures will quickly show the warts on the one-line programs. To gain speed and shorter computation times, one will generally have to access the Tcl core distribution and Tcllib. Functions math::numtheory::isprime , math::numtheory::firstNprimes, and math::numtheory::primesLowerThan are available in the Tcllib math library. See Tcllib & Tklib core contents & math::numtheory Category Numerical Analysis.
Important Note
gold 6/8/2021 update. Important Note. This page were largely developed under the earlier TCL4, ETCL, and TCL8.~~ versions on an outdated personal computer. This page is not a replacement for the current TCL core and TCLLIB with much improvement since TCL4 and other <faster> language constructs. See better routines and current methods for angle reduction, sin, cos, pi, etc in the TCL core distribution and TCLLIB. As of Jul2018, the TCLLIB has developed code for trig angles in degrees, trig inverse, and hyper functions in degrees, and angle reduction in radians and degrees. This supplemental trig.tcl, trigtest.tcl, and trig.man code is posted on the TCLLIB website. This math::trig.tcl seems really exciting work, which will keep TCL in pace with some of the other brand name languages (math oriented, I mean). Some of the TCL library code is posted as pending on the TCLLIB website, and sometimes not really in the main TCL distribution yet, so its worthwhile to investigate and run searches on the pending TCLLIB code, the SourceForge bins, and [L1 ] locations also. The TCLLIB math library is generally quicker and more accurate by a third over some homebrew code, see math::mean , Additional math functions, [L2 ]. The numerous examples on this wiki page include code lines that might be incompatible, inefficient, recursion limited, dead_weights, or redundant if installed in the same program. The local math procedures in scripts and one-line procedures may not be as fast and efficient as importing mathop , mathfunc, and math from TCLLIB and SourceForge, so check with the precompiled code in the TCL core and TCLLIB libraries >> first <<, then homebrew your one liners programs and scripts in TCL.
Pseudocode Section
# **********Extensions from gold **********
source playing_recursion_V2.tcl
# Suggest maintain air gaps, dead spaces, brackets;#-- >= greater than or equal to logic function
func >= {m n} {[= $n 0]? 1: [= $m 0]? 0: [>= [pred $m] [pred $n]]}
#-- > greater than logic function
func > {m n} {[= $m $n]? 0: [>= $m $n]}
proc flipper n { [expr {$n * -1 } ] }
# func abs n { [> $n 0]? $n: [< $n 0]? [ flipper $n]:0}
set sgn5 [expr {$x>0? 1 : $x<0? -1 : 0}] ;# RS
proc sgn5 x {set temp [expr {$x>0? 1 : $x<0? -1 : 0}]} ;# RS
proc sgn x {expr {($x>0) - ($x<0)}} ;# RS & rmax
proc sgn7 nn { if {$nn>0} { return 1 } elseif {$nn<0} { return -1 } else { return 0 }}
time { sgn7 7 } 5000 ;# 0.4554 microseconds per iteration.
#-- triangular number. Tricky code
# and Suggest maintain air gaps, spaces, brackets
func tri { n} {[< $n 2]? 1: [/ [* $n [+ $n 1] ] 2 ]}
test {tri 3} 6 {tri 2} 3 {tri 5} 15
#-- factorial recursion, but quickly exceeds domain
# fac is recursion limited, & excessive time beyond factorial 7
func fac n {$n<2? 1: [* $n [fac [pred $n ]]]}
#-- min, max, basic integer funcions
# but may need some error checks
# for entry zeros and equality, $m = $n
func min {m n} {$m<$n? $m: $n}
func max {m n} {$m>$n? $m: $n}
# zero_killer function swaps points of zero
# for 0.0000001 in observed data to avoid
# computer division by zero
func kzero { n } {[= $n 0]? 0.0000001: [= $n 0.]? 0.0000001: $n }
# ******* end extensions ************Console Session from Namespace ::liner
# under Pseudocode Section
namespace eval ::liner {
namespace export math
}
proc ::liner::convert { } { ;# before Playing Recursion deck
# yada yada } ;# after Playing Recursion deck
***** enter >::liner::convert< for invoking namespace **********
***** enter >::liner::demo< for code test **********
********* but considerable lengthy recursions ****
(System) 1 % ::liner::convert
(System) 2 % ::liner::demo
example >> gcd 12 24 -> 12, & expected was 12
example >> gcd 12 18 -> 6, & expected was 6 ;# ommitted lengthy reply here
info commands ::liner::*(System) 2 % ::liner::sgn ::liner::fac ::liner::sum_tri ::liner::pred ::liner::prime ::liner::abs ::liner::gcd ::liner::' ::liner::test ::liner::<= ::liner::test1 ::liner::convert ::liner::flipper ::liner::* ::liner::kzero ::liner::>= ::liner::+ ::liner::min ::liner::| ::liner::rem ::liner::< ::liner::func ::liner::demo ::liner::- ::liner::pred2 ::liner::= ::liner::max ::liner::> ::liner::eq ::liner::succ ::liner::tri ::liner::prime2 ::liner::/
(System) liner::func square { n} {[< $n 2]? 1: [* $n $n ] }
# liner::square has lengthy recursion and too many nested evaluations beyond 30
(System) 4 % liner::square 5 ;# returns 25
(System) 4 % liner::square 30 ;# returns 900
# liner::cube has lengthy recursion and too many nested evaluations beyond 10
(System) 8 % liner::func cube { n} {[< $n 2]? 1: [* [* $n $n ] $n ]}
(System) 9 % liner::cube 2 ;# returns 8
(System) 10 % liner::cube 4 ;#returns 64
(System) 11 % liner::cube 5 ;# returns 125
# func rectangle_area is test of redundant logic with 5 elements
liner::func rectangle_area {l w} {[= $l 0]? 0: [= $w 0]? 0: [* $l $w]}
(System) 13 % liner::rectangle_area 5 10 ;# returns 50
# constant for golden section, have to exactly name sqrt inside mathfunc::
liner::func gm { n} {[< $n 2]? 1: [expr (1 + [::tcl::mathfunc::sqrt 5] )*.5]}
liner::test {liner::gm 4 } 1.618033988749895
example >> liner::gm 4 -> 1.618033988749895, & expected was 1.618033988749895
# Playing Recursion was written originally for integers.
# But now passing pointing point calculations thru ::liner::func
# The global namespace is recognizing the func liner::gm.
set rook [liner::gm 4] ;# returns 1.618033988749895
# guess could put in a switch for ::liner::func to pass on floating points?
# or manually swap function calls
liner::func rectangle_area2 {l w} {[= $l 0]? 0: [= $w 0]? 0: [::tcl::mathop::* $l $w]}
(System) set house [ liner::rectangle_area2 5.2 10.1 ] ;# returns 52.52
# reciprocal func r! has several exceptions , [= $mm 0]? avoid division by zero
# reciprocal r! has exception , [= $mm 1]? defaults to 1
# exception tests performed before main calculation of 1/$mm
# maybe case liner::r! -2 -> -1 on negative integers has problem?
liner::func r! {mm} { [= $mm 0]? 0: [= $mm 1]? 1: [::tcl::mathop::/ 1 $mm] }
# Usage liner::r! 1 -> 1 ;# liner::r! 0 -> 0 ;# liner::r! 0.000001 -> 1000000.0
# liner::r! 0.000001 -> 1000000.0 ;# liner::r! -2. -> -0.5 if, if, and iffy Table
See section Noise Words of if by AMG. Seemed to call for a table, if one is studying recursion on one liner programs.
| table | printed in | TCL format | |
|---|---|---|---|
| elements | short hand for if | long hand for if | comment, if any |
| 2 | if a b | ;# if {a} then {b} | |
| 3 | if a b c | ;# if {a} then {b} else {c} | ;# 2*n+1 elements odd |
| 4 | if a b c d | ;# if {a} then {b} elseif {c} then {d} | |
| 5 | if a b c d e | ;# if {a} then {b} elseif {c} then {d} else {e} | ;# 2*n+1 elements odd |
| ***** | alternate | expressions for expr | **** |
| 8 | if a b c ...c1,c2,c3... d e | ;# if {a} then {b} elseif {c} ...elseif {c1} elseif {c2} elseif {c3} .... then {d} else {e} | multiple successive elseif?, but not seen example |
| 3 | a?b:c | expr equivalent;# if {a} then {b} else {c} ;# 2*n+1 elements odd | expr command has an internal if conditional ? in a?b:c |
| 5 | a?b:c?d:e | expr equivalent ;# 2*n+1 elements odd | expr command has an internal if conditional ? in a?b:c |
| 7 | a?b:c?d:e?f:g | expr equivalent ;# 2*n+1 elements odd | expr command has an internal if conditional ? in a?b:c |
| 9 | a?b:c?d:e?f:g?h:i | expr equivalent ;# 2*n+1 elements odd | expr command has an internal if conditional ? in a?b:c |
| 11 | a?b:c?d:e?f:g?h:i?j:k | expr equivalent ;# 2*n+1 elements odd | expr command has an internal if conditional ? in a?b:c |
McCarthy Symbolic Logic Table
Meaning symbols used in the McCarthy books and papers, along with equivalents mentioned on this TCL wiki page.
| table | printed in | TCL format | ||
|---|---|---|---|---|
| order of precedence for symbolic logic | name | conventional definition | possible McCarthy, alternate liner::proc on page , or TCL ‘equivalent | comment, if any |
| 1 | ( ) | connectives within parentheses | innermost parentheses first | |
| 2 | ‘ | negation | =!, ne, ! | hard to see on computer screen [L3 ] ,! = U+0021 |
| 3 | ^ | conjunction | U+2038 U+2227 ‸ CARET [L4 ][L5 ] | |
| 3 | ∨ | disjunction | U+2228 bottom hat not on some keyboards [L6 ][L7 ] | |
| 4 | -> | implication | [L8 ][L9 ] | |
| 5 | <-> | equivalence | = | U+21D4, U+2261, U+2194 |
| ******* | **** working list from symbolic logic **** | ***** | ||
| NA. | Universal quantification (For all X ) | |||
| NA. | Existential quantification (There exists X ) | |||
| NA. | Uniqueness quantification (There is a unique X ) | |||
| NA. | Non-existence quantification (There is no X )) | |||
| NA. | Numerical quantification (There are exactly n * X ) | |||
| NA. | Numerical quantification (There are at least n * X ) | |||
| NA. | Numerical quantification (There are at most n * X ) |
Table for List of Recursion Procs and Funcs
Includes procs and funcs mentioned on this TCL wiki page [L10 ] & Playing with recursion from RS.
| table | printed in | TCL format | ||
|---|---|---|---|---|
| subject | name | conventional definition | possible McCarthy func, alternate liner::proc on page , or TCL ‘equivalent | comment, if any |
| math | +,-,*,/ | math precedence | ||
| math | func | proc loads func expressions | ::liner::func | proc func {name argl body} {proc $name $argl list expr $body} ;# RS |
| math | test | proc test args | ::liner::test | multi-case tester: -RS |
| math | + | plus | ::liner::+ | add 2 elements, integer sum |
| math | - | minus | ::liner::- | subtract 2 integers, N1 => N2, difference defined only for ( m >= n) |
| math | * | multiply | ::liner::* | multiply 2 integers |
| math | / | divide | ::liner::/ | divide 2 integers , integer division |
| math | % | Integer division remainder | ::liner::rem | Integer division remainder (% in expr) |
| math | 1 | yes | logic value returned from some funcs | |
| math | 0 | no | logic value returned from some funcs | |
| math | -1 | negative | logic value returned from some funcs | |
| math | = | equal to | ::liner::eq , :liner::= | compare 2 integers, proc eq works for strings too |
| math | > | greater than | ::liner::> | compare 2 integers |
| math | < | lesser than | ::liner::< | compare 2 integers |
| math | => | lesser than or equal to | ::liner::>= | compare 2 integers |
| math | =< | lesser than or equal | ::liner::<= | compare 2 integers |
| math | =! | not equal | ::liner::=! , ::liner::=! | compare 2 integers |
| math | n+1 | increment | ::liner::succ, ::liner::' | similar function to TCL incr command |
| math | n-1 | decrement, the non-negative integer before n | ::liner::pred | similar function to TCL incr command |
| math | 2X | double | ::liner::int_2x | |
| math | 3X | triple | ::liner::int_3x | |
| math | 1/X | reciprocate | reciprocate ::liner::r! | |
| math | n! | factorial | ::liner::fac | |
| math | fib(n) | Fibonacci Number n | ::liner::fib | |
| math | * -1. | flips sign | ::liner::flipper | |
| math | $X * $X | square | ::liner::square | |
| math | $X * $X * $X | cube | ::liner::cube | |
| math | Phi | golden ratio constant | ::liner::gm | -> 1.618033988749895 |
| math | phi | golden ratio conjugate | ::liner::golden_ratio_conjugate | -> 0.618033988749895 |
| math | gcd | greatest common denominator | ::liner::gcd | argument of two elements |
| math | tri | triangle number | ::liner::tri | |
| math | sgn | sign | returns sign logic, 1 for positive number, 0 for 0, -1 for negative, used in validation logic Modeling COND with expr | |
| math | sum_int | sum of integers to n | ::liner::sum_int {n} | returns sum of integers to n |
| math | sum_squares | sum of squares | ::liner::sum_squares {n} | returns sum of squares to n |
| math | sum_cubes | sum of cubes | ::liner::sum_cubes {n} | ;# formula for Sum of Cubes is (n**2) ((n + 1)**2) / 4 |
| math | sum_4th_power | sum of 4th powers | ::liner::sum_4th_power {n} | formula sum_4th_power = n* (n+1)* (2*n+1 )* ( 3*n**2 + 3*n -1)/30 |
| math | sum_5th_power | sum of 5th powers | liner::sum_5th_power | ;# formula sum_5th_power = n*n* (n+1)* (n+1 )* ( 2*n**2 + 2*n -1)/12 |
| math | kzero | zero killer | ::liner::kzero | $n == 0, replace by 0.0000001 , used to avoid division by zero in observed data |
| math | max | maximum | ::liner::max | maximum of 2 numbers |
| math | min | minimum | ::liner::min | minimum of 2 numbers |
| math | prime | test n for prime | ::liner::prime | 1 for prime zero for non-prime, defined for integers, similar to TCL wiki isprime Primes |
| math | prime2 | helper func to prime | ::liner::prime2 | integer helper func to prime |
| math | abs | absolute value | ::liner::abs | returns absolute value from one number, TCL expr abs |
| math | pi | circle constant | liner::pi -> 3.141592653589793 | proc pi {} {expr acos(-1)} ;# AMG |
| math | fix | circle constant experiment ;# returns pi from atan formula with 2 terms | ::liner::fix | proc fix {} {expr {4. * (atan(1./fib2 3) + atan(1./fib2 4))}} |
| math | IsEven | even logic test | liner::IsEven | if even , return logic 1, if odd, return logic 0 |
| math | IsOdd | odd logic test | liner::IsOdd | if odd, return logic 1, if even, return logic 0 |
| math | IsPositive | positive logic test | liner::IsPositive | if positive , return logic 1, if negative, return logic 0 |
| math | IsNegative | negative logic test | liner::IsNegative | if positive , return logic 0, if negative, return logic 1 |
| math | tri | triangular number | ||
| math | trix | triangular number multiplication | ||
| math | ||||
| math | ||||
Also Ref. Mathematical Structures for Computer Science, Judith L. Gersting, Indiana University, 2014
Screenshots Section
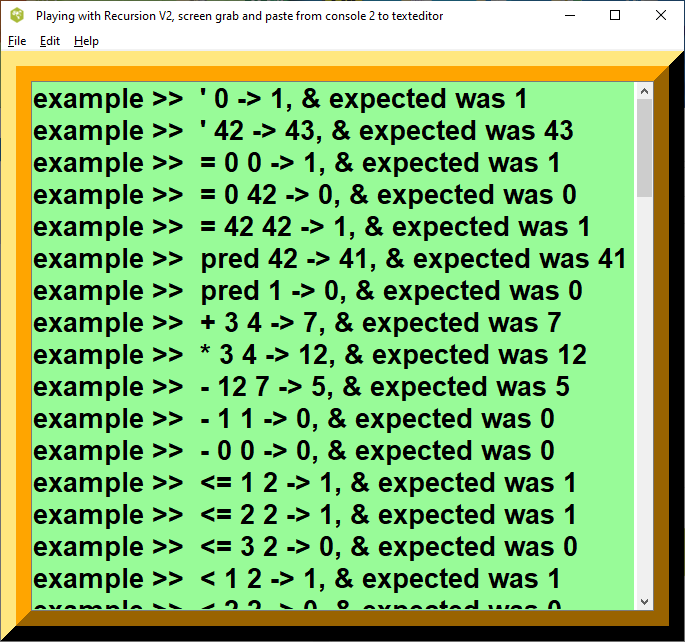
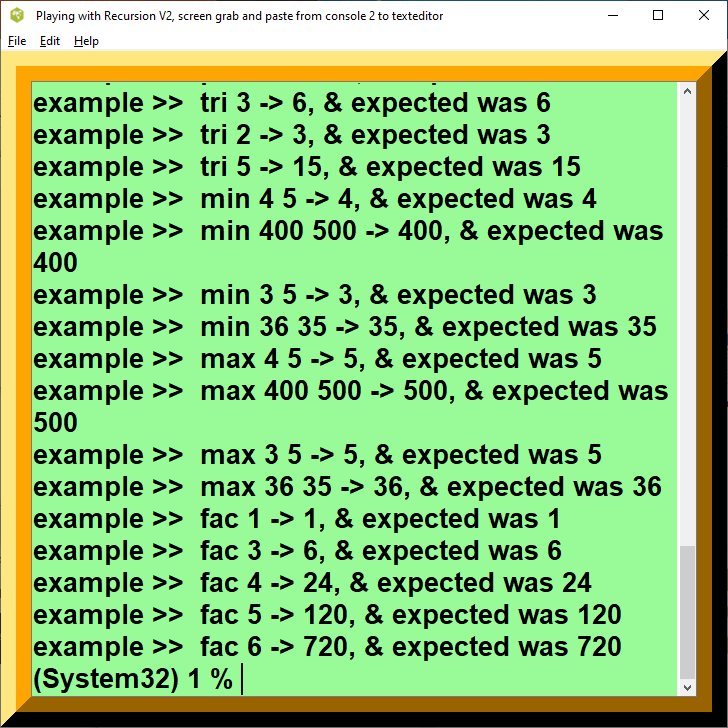
Figure 1. Playing Recursion Screenshot 1
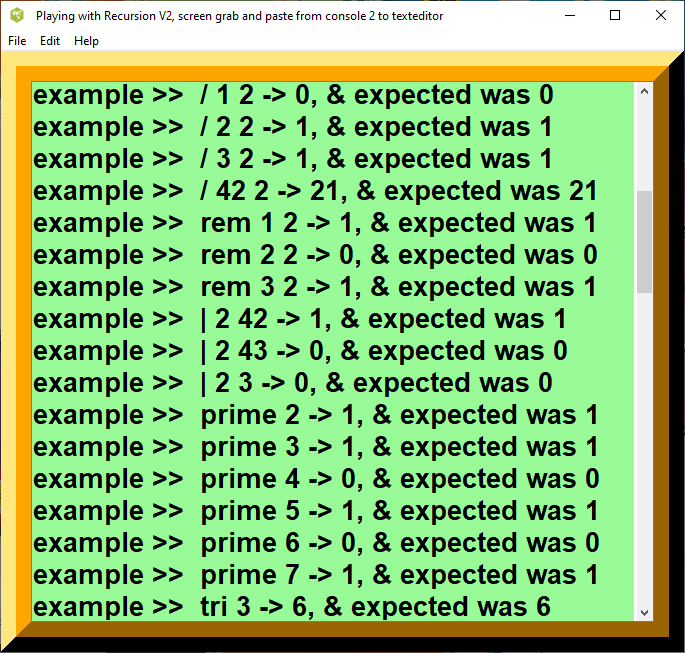
Figure 2. Playing Recursion Screenshot Two
Figure 3. Playing Recursion Screenshot Three
Figure 4. Playing Recursion V2 triangle function
Figure 5. Playing Recursion V2 step function
Figure 6. Playing Recursion V2 triangle wave function
An example is the triangle wave function centered at the origin. These are linear equations for the wave near the origin, but the slope constants of the wave can be different in sign and magnitude. Slopes with different -/+ signs and equal magnitude are shown. The condition domains for the triangle wave function might be:
- $variable < -1
- -1 < $variable with negative slope -$s1 < 0
- $variable = 0
- 0 < $variable with positive slope +$s2 < 1
- $variable > 1
Figure 7. Playing Recursion V2 positive step function
As another example for the positive rectangle step function, the condition domains might be:
- $variable = 0 d < 0
- $variable = 0 d = 0
- 0 < positive $variable < 1
- $variable = 0 d > 1
Figure 8. Iteration on Canvas
Figure 9. Factorial Function N!
Testcases Section
Testcase 1, step_function Starts at -1
| table | printed in Tcl format | |
|---|---|---|
| session | proc & mean value | comment, if any |
| -2.0 | step_function 0 | |
| -1.8 | step_function 0 | |
| -1.6 | step_function 0 | |
| -1.4 | step_function 0 | |
| -1.2 | step_function 0 | |
| -1.0 | step_function 1 | 1st breakpoint |
| -0.8 | step_function 1 | |
| -0.6 | step_function 1 | |
| -0.4 | step_function 1 | |
| -0.2 | step_function 1 | |
| 0.0 | step_function 1 | zero point |
| 0.2 | step_function 1 | |
| 0.4 | step_function 1 | |
| 0.6 | step_function 1 | |
| 0.8 | step_function 1 | |
| 1.0 | step_function 1 | 2nd breakpoint |
| 1.2 | step_function 0 | |
| 1.4 | step_function 0 | |
| 1.6 | step_function 0 | |
| 1.8 | step_function 0 | |
| 2.0 | step_function 0 | |
| 2.2 | step_function 0 | |
| 2.4 | step_function 0 | |
| 2.6 | step_function 0 | |
| 2.8 | step_function 0 | |
| 3.0 | step_function 0 |
Testcase 2, step_function Starts at Zero
| table | printed in Tcl format | |
|---|---|---|
| session | proc & mean value | comment, if any |
| -2.0 | step_function 0 | |
| -1.8 | step_function 0 | |
| -1.6 | step_function 0 | |
| -1.4 | step_function 0 | |
| -1.2 | step_function 0 | |
| -1.0 | step_function 0 | |
| -0.8 | step_function 0 | |
| -0.6 | step_function 0 | |
| -0.4 | step_function 0 | |
| -0.2 | step_function 0 | |
| 0.0 | step_function 1 | 1st breakpoint |
| 0.2 | step_function 1 | |
| 0.4 | step_function 1 | |
| 0.6 | step_function 1 | |
| 0.8 | step_function 1 | |
| 1.0 | step_function 1 | 2nd breakpoint |
| 1.2 | step_function 0 | |
| 1.4 | step_function 0 | |
| 1.6 | step_function 0 | |
| 1.8 | step_function 0 | |
| 2.0 | step_function 0 |
Testcase 3, Impulse step_function Starts at Zero
| table | printed in Tcl format | |
|---|---|---|
| session | proc & mean value | comment, if any |
| -2.0 | step_function 0 | |
| -1.8 | step_function 0 | |
| -1.6 | step_function 0 | |
| -1.4 | step_function 0 | |
| -1.2 | step_function 0 | |
| -1.0 | step_function 0 | |
| -0.8 | step_function 0 | |
| -0.6 | step_function 0 | |
| -0.4 | step_function 0 | |
| -0.2 | step_function 0 | |
| 0.0 | step_function 1 | 1st breakpoint at zero |
| 0.2 | step_function 1 | 2nd breakpoint at zero plus small amount |
| 0.4 | step_function 0 | |
| 0.6 | step_function 0 | |
| 0.8 | step_function 0 | |
| 1.0 | step_function 0 | |
| 1.2 | step_function 0 | |
| 1.4 | step_function 0 | |
| 1.6 | step_function 0 | |
| 1.8 | step_function 0 | |
| 2.0 | step_function 0 |
Testcase 4, One Liner Programs Approach to the Fibonaci series
AMG posted me a really good recursion proc on the Fibonaci series. I have recast this proc into the Playing Recursion namespace ::liner. Now the construction of a recursion problem can be sequenced into generic steps. -> is the return symbol. fib(n) is the Fibonaci function and f(n) is the generic function.
- n! = n*(n-1)*(n-2)*(n-3) ... 3*2*1
- (n-1)! = (n-1)*(n-2)*(n-3) ...3*2*1
- int fac (int 0) -> 1
- fib (1) = f(1) if n=> 1, -> 1
- fib (0) = f(0) else {-> 1 }
- fib (n) = f(1) -> 1
- fib (4) = f(4) -> 4 * fib (3)
- fib (3) = f(3) -> 3 * fib (2)
- fib (2) = f(3) 2 * fib (2-1) -> 2! * fib (1) = 2 * 1 = 2
# AMG proc w/a?b.c recast to func inside namespace liner::
proc fib2 {n} {expr {$n < 2 ? $n : [fib2 [expr {$n - 1}]] + [fib2 [expr {$n - 2}]]}} ;# AMG
# func has little different notation but understandable
func fib { n } {[< $n 2 ]? $n: [+ [fib [- $n 1 ]] [fib [- $n 2 ]] ]}
# Usage fib 2 ;# returns 1 fib 5 ;# returns 5
# Usage fib 10 ;# returns 55Testcase 5, One Liners Programs Approach to the Golden Section
Continuing with the really good recursion proc AMG posted me. This proc can be recast or morphed into the Playing Recursion namespace ::liner. In the higher Fibonaci numbers, the ratio or dividend of successive Fibonaci numbers fib(n)/ fin(n-1) begins to approximate' the Golden Section or Golden Mean. An exact solution func gm was loaded into the namespace::liner (1+sqrt(5))*.5 = 1.618033988749895. One may develop a liner::func for approximating the Golden Section using recursion.
However, since lengthy recursion calls are anticipated, lets check the speed of the AMG proc which used the expr method. Using mathop in part of the proc fib3 in global space does save about 1 microsecond.
Initial trial calculations: Hand calculations for fib3 (38) = 39088169 over (fib3 37) = 24157817, expr (1.*39088169) / 24157817 returns 1.618033988749894. The textbook value for phi was 1.618033988749895. The golden ratio conjugate approximates (fib3 37) = 24157817 over fib3 (38) = 39088169, expr (1.*24157817) / 39088169 -> 0.6180339887498951. The textbook value for 1/phi was 0.618033988749895
The golden ratio conjugate is 1/phi or phi-1 is 0.618033988749894. One can develop the golden ratio conjugate by installing the reciprocal fib(n-1)/ fin(n) into liner::func golden. The formula pi =~ 4 * sqrt phi can be used to approximate pi through the golden section. Steve Lautizar posted pi =~ 6/5 * Phi^2, which looks easier to implement in Playing Recursion. expr { (6./5)*1.618033988749894*1.618033988749894 } returns 3.1416407864998708.
# AMG proc w/a?b.c recast to func inside namespace liner::
proc fib2 {n} {expr {$n < 2 ? $n : [fib2 [expr {$n - 1}]] + [fib2 [expr {$n - 2}]]}} # AMG
time { fib2 10 } 1000 # fib2 10 -> 65.842 microseconds per iteration
proc fib3 {n} {expr {$n < 2 ? $n : [fib3 [- $n 1]] + [fib3 [- $n 2]]}} # AMG
time { fib3 10 } 1000 # fib3 10 -> 64.722 microseconds per iteration
# using mathop in part of the proc does save about 1 microsecond
# func has little different notation from the liner:: rules but understandable
liner::func golden { n } { [::tcl::mathop::/ [fib $n] 1. [fib [- $n 1]] ]}
# liner::golden 10 # -> 1.6176470588235294, liner::golden 18 # -> 1.6180338134001253
# but the liner::golden was recursion limited to 18,
# analysis went back to a proc in global space to further check the solution
proc golden2 { n } { [/ [fib3 $n] 1. [fib3 [- $n 1]] ]}
# golden2 20 # -> 1.6180339631667064
golden2 38 # -> 1.618033988749894 was highest fib($n)/fib($n-1) without cobwebs on programmer
# installing the reciprocal '''fib(n-1)/ fin(n)''' into liner::func golden and proc golden2
liner::func golden_ratio_conjugate { n } { [::tcl::mathop::/ [fib [- $n 1]] 1. [fib $n] ]}
# Usage liner::golden_ratio_conjugate 18 -> 0.6180340557275542
proc golden2_ratio_conjugate { n } { [/ [fib3 [- $n 1]] 1. [fib3 $n ] ]}
# Usage golden2_ratio_conjugate 18 # -> 0.6180340557275542 reasonable time delay
# Usage golden2_ratio_conjugate 38 # -> 0.6180339887498951 cobwebs fallingFigure 10. Fibonaci small numbers
Figure 11. Fibonaci large numbers
Testcase 6, One Liners Programs Approach to the Approximate Pie
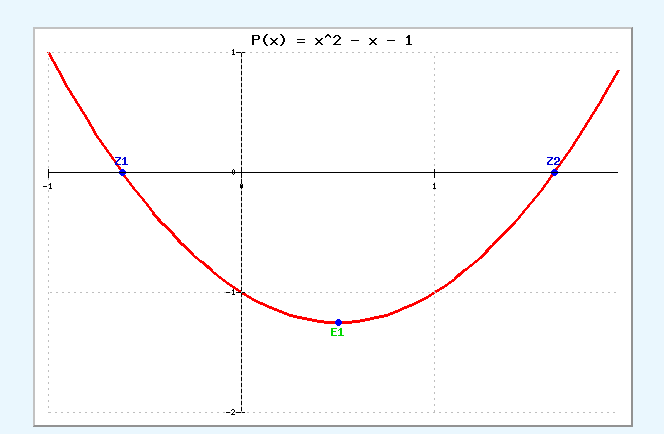
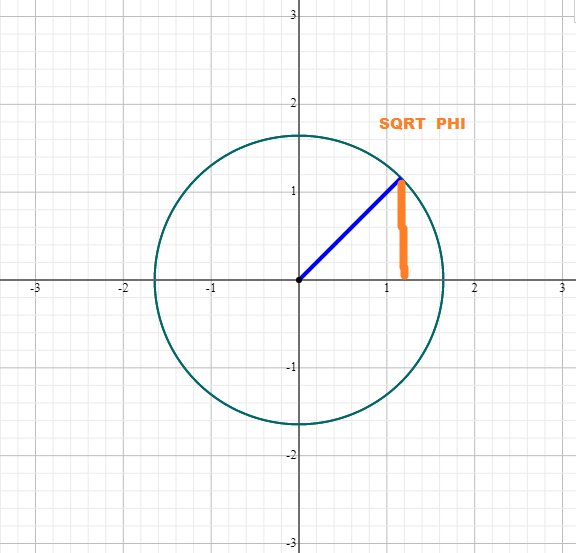
The analysis starts out with with the AMG proc for pi using acos -1, which returns 3.141592653589793 correct. We would like to develop a recursive formula for pi in the liner:: testbed. The formula pi oc 4 * sqrt (phi_conjugate) or pi oc 4 * sqrt (1/phi) can be used to approximate pi through the golden section phi. The formula expr 4. * sqrt (1/1.618033988749894) returns 3.144605511029694. Something wrong, contra-check was expr 4.* sqrt (0.618) -> 3.144. Steve Lautizar posted pi =~ 6/5 * Phi^2, which looks easier to implement in Playing Recursion. The trial calculation { (6./5)*$phi*$phi } returns 3.14164, pi to 2 decimal places. Subbing the exact formula for phi gives another avenue, phi = expr (1+sqrt(5))*.5, pi =~ expr (6./5)*(((1+sqrt(5))*.5)**2)
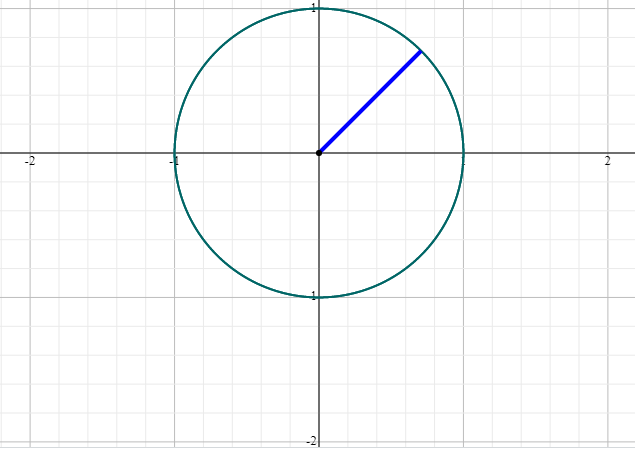
The positive root and negative conjugate root to the minimal polynomial x**2 − x − 1 is phi 1.61803 and -0.618033. There was a graphical method for finding square roots using circle and inner right triangle on the number line. Rene Descartes gave a proof from symmetric triangles. The circle radius was n; the circle radius was 2*n; the center of circle was positioned at N on the number line;the adjacent side of the triangle was 2*N-1; the opposite side of the triangle was sqrt (2n-1). For our problem and somewhat expanding the unit circle with radius of 1 from X**2 + y**2 = 1. The new circle equation is X**2 + y**2 = 1.616. The opposite side of triangle is sqrt phi. We can see the vector lies in or near the pi/4 sector or arc length, which may give the pi/4 or 45 degree factor in the problem.
# procs below should should be pastable into TCL Console
proc pi {} {expr acos(-1)} # AMG
# Usage pi # returns 3.141592653589793 correct
# expr 4.* sqrt (0.618) -> 3.1445190411253674 phi conjugate formula
proc approx_pie2 { } {expr 4.* sqrt (.618033988749894) }
# Usage approx_pie2 #; 3.144605511029691 approximate pi to 2 decimal places
# Note approx_pie2 number slightly above correct answer?
proc approx_pie { n } { [* [/ 6. 5] [** [/ [fib3 $n] 1. [fib3 [- $n 1]]] 2]]}
# Usage approx_pie 20 # -> 3.141640 approximate pi to 3 decimal places
# Note approx_pie number slightly above correct answer?
proc pix { } {return [expr { (4. * ( [atan .5] + [atan [/ 1 3.] ]))}]}
# exact double atangent formula from Euler
# Using expr methods on *,+,& atan archtangent
proc pieatan2 { } {return [expr { (4. * ( atan(.5) + atan(1/ 3.) ))}]}
# using mathop method on *&+ and mathfunc method on atan
proc pieatan { } { return [* 4. [+ [atan .5] [atan [/ 1 3.] ] ] ]}
# Usage proc pieatan { } # returns 3.141592653589793 exact
time {pieatan} 5000 # 1.1686 microseconds per iteration,
# fairly fast using both mathop and mathfunc calls
# pi formula from Jorge Xerxes
[* 2 [+ [atan [/ 1. [sqrt .618033988749894]]] [atan [sqrt .618033988749894]] ]]
# returns 3.141592653589793
# piex passes through namespace liner::
liner::func piex {} {[* 2. [::tcl::mathfunc::+ [::tcl::mathfunc::atan [/ 1. [::tcl::mathfunc::sqrt .618033988749894]]] [::tcl::mathfunc::atan [::tcl::mathfunc::sqrt .618033988749894]] ]]}testing recursion on infinite series pi = 4* atan(fib(2*$n+1)], 1 < f($n) terms < $n
# following under test
# proc fib3 has to be loaded first
proc fib3 {n} {expr {$n < 2 ? $n : [fib3 [- $n 1]] + [fib3 [- $n 2]]}} # AMG
proc pie5 {} {expr {4* (atan(1./[fib3 3]) + atan(1./[fib3 4]))}}
# Usage pie5 # 3.141592653589793 # 2 terms for atan(1./[fib3 $n] series
# checking terms for infinite series atan(fib(2*$n+1)]
proc fix2 {n} {expr {$n < 2 ? $n : [fix2 [expr 4* (atan(1./[fib3 [expr 2*$n+1]]))]]}}
# Usage fix2 3 -> 0.30708756507911217 terms of infinite series
proc fix3 {n} {expr {$n < 2 ? $n :[- [fix [expr 4* (atan(1./[fib3 [expr 2*$n+1]]))]] [fix [expr 4* (atan(1./[fib3 [expr 2*$n+1+2]]))]] ] }}
foreach i {1 2 3 4 5 6 7 8 9} {lappend rook [fix $i] };$rook' set rook {}
proc vik {n} { return [expr { 8./ ((4.*$n+1. )*( 4.*$n+3. ))}]}
# Usage vik 7 -> 0.008898776418242492 # individual terms for pi series
foreach i {1 2 3 4 5 6 7 8 9} {lappend rook " [vik $i] + " };$rook ; set rook {}
# following is experimental kludge combination,
# but some of the atan series for pi have
# 2,3,4, or more terms, which can be
# zeroed out or fill in the blanks.
proc fix {n} {expr {$n < 2 ? $n : [fix [expr {.000001* atan ( 1. / (2.*$n-1) )+ .0000001* atan ( 1. / (2.*$n-1) )}]] + [- [* 16. [atan [/ 1. 5]]] [* 4. [atan [/ 1. 239]] ] ]}}
# Usage fix 3 # -> 3.1415928509853535
# Chinese fractions for pi from Zu Chongzhi, fifth century, 429-500 CE
# Jiu zhang suanshu, Nine chapters of the mathematical art
liner::func pie_poly2 {} {[::tcl::mathop::/ 355. 113. ] } # liner:: namespace use
proc pie_poly {} {[/ 355. 113.]} # global namespace use
# Usage pie_poly # -> 3.1415929203539825 accurate to 6 places
# TCLLIB integration of expr expression in x
# of OEIS formula for pi, ref notes on sequence A003881
proc pie_tcllib {} {set return [::math::calculus::integralExpr 0 100 10000 {(4.* $x)/($x**4 + 1)}]}
# Usage pie_tcllib -> 3.1413926535904273
proc piez {} {[expr {4.*atan (1./sqrt(2))+2.*atan(1./sqrt(8))}]}
# Usage piez # returns 3.141592653589793- Phi**3=2*phi+1
- Phi**4=3*phi+2
- Phi**5=5*phi+3
- Phi**6=8*phi+5
Figure 12. minimal polynomial x**2 − x − 1
- minimal polynomial x**2 − x − 1
Figure 13. Unit Circle
- unit circle, radius =1, circle equation x**2 + y**2 = 1**2
Figure 14. Circle with radius of phi
- for circle with sqrt phi, radius =1.616 , circle equation x**2 + y**2 = phi
- subbing sqrt into equation x**2 + y**2 = (sqrt phi)**2
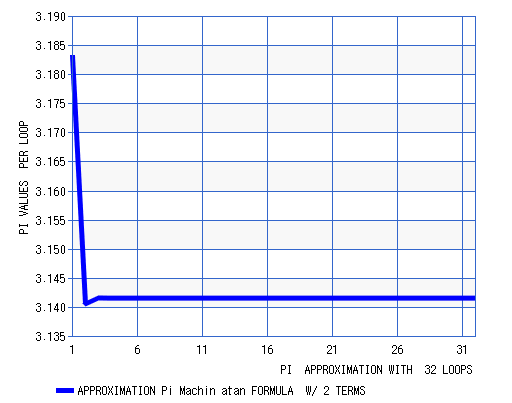
Figure 15. MACHIN PI 2 TERM FORMULA ed2
Testcase 7, Polynomials, Sum of Integers, Sum of Squares, Sum of Cubes, and Sum of Nth Powers
The formula for Sum of Integers is n*(n+1)/2. The formula for Sum of Squares is n*(n+1)*(2*n+1)/6. Initial code reporting too many nested evaluations with 4 terms in row. Added helper procs to contend with this.
# base functions loaded into namespace liner::
proc eq {m n} {string equal $m $n} # RS
proc succ x {incr x} # RS
# liner:: has shorter symbolic names
# for the two basic functions:
proc ' x {incr x} # RS
proc = {m n} {string equal $m $n} # RS
# formula for Sum of Integers is n*(n+1)/2
# initial sum of integers code
# reporting endless loops with w/4 terms
liner::func sum_int { n} {[< $n 2]? 1: [expr [/ [* $n [succ $n ]] 2 ]]}
# Usage liner::sum2 3 # -> 6 correct for sum 1 + 2 + 3
# helper functions 2X and 3X,
# following liner:: rules
liner::func int_2x { n} {[< $n 1]? 1: [expr [* $n 2 ]]}
liner::func int_3x { n} {[< $n 1]? 1: [expr [* $n 3 ]]}
# formula for Sum of Squares is n*(n+1)*(2*n+1)/6
liner::func sum_squares { n} {[< $n 1]? 1: [expr [/ [* [* $n [succ $n ]] [succ [int_2x $n] ] ] 6 ]]}
# Usage liner::sum_squares 3 # -> 14 correct for sum 1 + 4 + 9Scratch Code on Sum of Cubes
# formula for Sum of Cubes is (n**2) ((n + 1)**2) / 4
func sum_cubes { n} {[< $n 1]? 0:[= $n 1]? 1: [expr [/ [* [* $n $n] [* [succ $n] [succ $n] ] ] 4 ]]}
# defined for positive integers, two ? conditionals in expr
# Usage sum_cubes 0 -> 0, sum_cubes 1 -> 1, sum_cubes 2 -> 9Scratch Code on Sum of 4th Powers
func sum_4th_power2 reporting errors on too many nested evaluations (infinite loop?) inside the liner:: namespace. The TCL proc using the expr method is working well. The two helper funcs are working well inside liner:: namespace, but when the helper funcs are combined, the func sum_4th is reporting too many nested evaluations. Maybe have to go to conventional multiple statement proc to work around.
# formula sum_4th_power = n* (n+1)* (2*n+1 )* ( 3*n**2 + 3*n -1)/30
# using integer arithmetic for the long digit answers
proc sum_4th_power {n} { expr { $n* ($n+1)* (2*$n+1 )* (3*$n**2 + 3*$n -1)/30}}
# Usage sum_4th_power 0 -> 0 # Usage sum_4th_power 1 -> 1
# Usage sum_4th_power 1000 -> 200500333333300
# Usage sum_4th_power 200 -> 64802666660
# Usage sum_4th_power 1000000000
# -> 200000000500000000333333333333333333300000000
func helper {n } { [ + [ int_3x [square $n] ] [pred [ int_3x $n ]]]}
func helper2 {n} { [* $n [* [ succ $n ] [succ [int_2x $n ]]]] }
func sum_4th_power2 { n} {[< $n 1]? 0:[= $n 1]? 1: [expr [/ [* [helper $n] [helper2 $n] ] 30 ]]}
proc tester_4x {n} {
if { [< $n 1] } { set res 0; break}
if { [= $n 1] } { set res 1; break}
set term1 [helper $n]
set term2 [helper2 $n]
set res [expr { ($term1 * $term2 ) / 30 } ]
}
# Usage liner::tester_4x 5 -> 979
# reporting nested evals after 5Scratch Code on Sum of 5th Powers
# formula sum_5th_power = n*n* (n+1)* (n+1 )* ( 2*n**2 + 2*n -1)/12
proc sum_5th {n} {return [expr {($n*$n* ($n+1)*($n+1 )*(2*($n**2)+2*$n-1))/12}] }
# internal ? in expr testing for 2 conditions
proc sum_5th_power {n} {expr { $n < 1? 0: $n > 1 ? 1 : ($n*$n* ($n+1)*($n+1 )*(2*($n**2)+2*$n-1))/12}}
# Usage sum_5th_power 0 -> 0 ;# Usage sum_5th_power 1 -> 1
# Usage sum_5th_power 2 -> 33Testcase 8, Triangular Number Multiplication
The Glaisher formula returns the triangular multiplication product TNX as an integer from two positive natural numbers. Triangular multiplication is formulated as aa * bb = TN <aa-1> + TN <bb> - TN <aa-bb-1>. The Glaisher formula does not define the Triangular Number for negative numbers. As understood here, the term TN <aa-bb-1> might return negative numbers for bb > aa, so suggest swap or reorder to avoid TN<-n>. The original liner::- subtraction calls for $m > $n. However, it should be possible to redefine subtraction in liner::- for both cases $m > $n and $n > $m, but hate to monkey too much with original RS code. Maybe a dual subtraction based on liner::func max could be called as a helper function. For now, using m > n in liner::func for triangular multiplication.
Test. for TNX 6 3, the first term is 15, the second term is 6, and the third term is 3. Glaisher formula gives 15+6-3 equals 18, correct.
Scratch Code on triangular multiplication product
# TNX = aa * bb = TN <aa-1> + TN <bb> - TN <aa-bb-1>
# may need some helper functions inside liner:: if n>m
# for now, m > n
liner::func max {m n} {$m>$n? $m: $n}
# -- the difference (defined only for m >= n)
func - {m n} {[= $n 0]? $m: [- [pred $m] [pred $n]]}
# test {- 12 7} 5 {- 1 1} 0 {- 0 0} 0
liner::func first_term {m n} { [+ [tri [pred $m ]] [tri $n]] }
liner::first_term 5 3 # -> 16
liner::func third_term {m n} { [tri [- [- $m $n ] 1 ] ] }
liner::third_term 5 3 # -> 1
liner::func trix {m n} { [- [+ [tri [pred $m ]] [tri $n]] [tri [- [- $m $n ] 1 ] ] ]}
# Usage liner::trix 5 3 -> 15 # m > n because subtraction call for this
# Usage liner::trix 30 5 -> 150 # m > n
# but too many nested evals beyond m = 30References
- Playing with Recursion by RS
- Functional Programming
- recursion
- func
- Recursive functions
- John McCarthy: A basis for a mathematical theory of computation, in:
- Computer Programming and Formal Systems.
- P.Braffort, D.Hirschberg (ed.), Amsterdam:North Holland 1963,
- several versions, archived pdf [L11 ]
- McCarthy’s LISP and Basis for Theory of Computation, archived pdf[L12 ]
- en.wikipedia.org search on <John McCarthy computer> [L13 ]
- John McCarthy at Stanford web site, archived [L14 ]
- Towards a Mathematical Science of Computation, J. McCarthy,
- Computer Science Department,Stanford University, archived pdf [L15 ]
- Elephant 2000: A Programming Language Based on Speech Acts
- John McCarthy, Stanford University, archived [L16 ]
- Elephant input and output statements are characterized
- as speech acts and programs, which
- can refer directly to the past.
- Elephant proposal contains summary
- on McCarthy mathematical theory of computation
- Mysteries and other Matters, development of Lisp , archived [L17 ]
- King that learns? A Program That Learns
- upvar sugar
- Salt and Sugar
- Math sugar
- A little math language
- args
- RS
- LV
- Tcl and LISP Richard Suchenwirth
- Radical Language Modification
- Functional Programming
- Custom curry
- Playing with recursion
- Modeling COND with expr
- Sample Math Programs
- Professor Frisby's Mostly Adequate Guide to Functional Programming [L18 ]
- expr shorthand for Tcl9
- Steps towards functional programming
- Tacit programming
- The fortran call statement appeared in Fortran2 (1958). example of call exit, fortran 4
- Thocp code, http://www.thocp.net/software/languages/fortran.htm
- Natural User Interface
- Natural Languages category
- Game kingdom of strategy
- wikipedia.org wiki The_Sumerian_Game
- Find all words
- Things German
- How to synthesize a query
- Writing Tk programs so that the user can extend or interact with them without modifying the application
- Ruslish
- Accumulator Generators
- Accumulator Generator
- Whadjasay
- disassemble byte code [L19 ]
- One Liners Programs Compendium [L20 ]
- One Liners
- Oneliner's Pie in the Sky
- Ref. WIKI BOOKS, Tcl_Programming_Introduction, [L21 ]
- Book Section contrasts one liners programs
- versus traditional procedural approach,
- Multiple Wiki Books on TCL programming [L22 ]
- if
- New Control Structures
- Kernighan and Pike: The practice of programming
References on Golden Ratio and pi Math
- Golden Ratio pdf [L23 ]
- Golden section ratio: Phi [L24 ]
- High quality Wolfram, Golden_Ratio [L25 ][L26 ]
- Mathematics Galore!, pub 2012 by James Tanton
- The golden ratio, Fibonacci numbers and BBP-type formulas,Kunle Adegoke†
- Department of Physics, Obafemi Awolowo University, Ile-Ife, Nigeria
- Random Fibonacci sequences and the number 1.13198824
- Author: Divakar Viswanath, Journal: Math. Comp. 69 (2000), 1131-1155
- Hayashi, Ko, Fibonacci Numbers and the Arctangent Function, manuscript (1995).
- Abel-Plana Formula [L27 ]
- The encyclopedia of integer sequences, hardcopy, , 1995 ,
- by N. J.A. Sloane & Simon Plouffe
- non-alternating infinite series pi/4 = expr 2./ (4.*$n+1. )*( 4.*$n+3. )[L28 ]
- The On-Line Encyclopedia of Integer Sequences® (OEIS®) Wiki [L29 ]
- OEIS notes on infinite series pi/4 = expr 2./ (4.*$n+1. )*( 4.*$n+3. )
- sequence A003881 [L30 ]
- From Peter Bala, Nov 05 2019: (Start)
- Quote . Pi/4 = k!*Sum_{n = -inf..inf} 1/((4*n+1)*(4*n+3)*...*(4*n+2*k+1))
- Equals Integral_{x = 0..inf} sin(x)^4/x^2 dx = Sum_{n >= 1} sin(n)^4/n^2,
- by the Abel-Plana formula.
- Equals Integral_{x = 0..inf} sin(x)^3/x dx = Sum_{n >= 1} sin(n)^3/n,
- by the Abel-Plana formula. Unquote (End)
- individual terms for pi series
- From Amiram Eldar, Aug 19 2020: (Start)
- Quote. Equals arcsin(1/sqrt(2)).
- Equals Product_{k>=1} (1 - 1/(2*k+1)^2).
- Equals Integral_{x=0..oo} x/(x^4 + 1) dx.
- Equals Integral_{x=0..oo} 1/(x^2 + 4) dx. unquote (End)
- A Viète-like formula for pi based on infinite sum of the arctangent functions with nested radicals
- posted on 03.01.2017, 21:34 by Sanjar Abrarov, Brendan Quine
- OEIS notes on Fibonaci sequence A000045 [L31 ]
- OEIS notes on atan related "sequence" expansion, A333691 [L32 ]
- OEIS notes on pi 3.14... related "sequence" expansions plural, A000796 [L33 ] & [L34 ]
- Pi: A Source Book, Lennart Berggren, Jonathan Borwein, and Peter Borwein,
- Third Edition, Simon Fraser University, July 5, 1999
- Mathematical Structuresfor Computer Science, 2014
- Discrete MatheMatics anD its applications, Judith L. Gersting,
- Indiana University-Purdue University at Indianapolis
Appendix Code
appendix Tcl programs and scripts
Console Program for Playing Recursion V2
demo examples for one liner programs
# pretty print autoindent from ased editor
# trial console operation
# Playing Recursion V2
# demo examples for one liner programs
# written on Windows 10 on ActiveTcl
# working under TCL version 8.6
# gold on TCL Club , 05ct2020
# console has large black type on green
# used as testbed for integer arithmetic
# Playing with Recursion V2 ???
# Playing with Recursion is TCL wiki page by RS
# < positive integers > function procs written by RS
# gold added cosmetics in console deck
package require Tk
package require math::numtheory
package require math::constants
package require math::trig
package require math
namespace path {::tcl::mathop ::tcl::mathfunc math::numtheory math::trig math::constants }
namespace path {::tcl::mathop ::tcl::mathfunc}
set tclprecision 17
# RS main deck
proc succ { x } {incr x}
# Note. procs succ and proc eq loaded in both decks
# for global and namespace ::liner::
# equality of integers in canonical form can,
# without using expr, be had as
proc eq {m n} {string equal $m $n}
# proc eq works with strings and numbers
# McCarthy advocates "conditional expressions",
# alternating sequences of {condition} {result} like
# A B C D ...
# which can in Tcl (and many other languages)
# be implemented as variables & conditionals
# if $A then $B elseif $C then $D ...
# or more compactly with expr's ?: ternary operator:
# $A? $B: $C? $D: ...
# using expr in these experiments only for the ?: operator
# before Playing Recursion deck
# begin namespace liner
namespace eval ::liner {
namespace export math
namespace path {::tcl::mathop ::tcl::mathfunc}
# before Playing Recursion deck RS
proc eq {m n} {string equal $m $n}
proc succ { x } {incr x}
proc func {name argl body} {proc $name $argl [list expr $body]}
# here's a tiny multi-case tester: -RS
# added puts for console result to original proc test1
proc test1 args {
foreach {case expected} $args {
catch {uplevel 1 $case} res
if {$res != $expected} {error "$case->$res, expected $expected"}
}
}
proc test args {
foreach {case expected} $args {
catch {uplevel 1 $case} res
if {$res != $expected} {error "$case->$res, expected $expected"}
puts "example >> $case -> $res, & expected was $expected"
}
}
proc demo {} {
test {gcd 12 24} 12 {gcd 12 18} 6 {gcd 17 19} 1
test {' 0} 1 {' 42} 43
test {= 0 0} 1 {= 0 42} 0 {= 42 42} 1
test {pred 42} 41 {pred 1} 0
test {+ 3 4} 7
test {* 3 4} 12
test {- 12 7} 5 {- 1 1} 0 {- 0 0} 0
test {<= 1 2} 1 {<= 2 2} 1 {<= 3 2} 0
test {< 1 2} 1 {< 2 2} 0 {< 3 2} 0
test {/ 1 2} 0 {/ 2 2} 1 {/ 3 2} 1 {/ 42 2} 21
test {rem 1 2} 1 {rem 2 2} 0 {rem 3 2} 1
test {| 2 42} 1 {| 2 43} 0 {| 2 3} 0
test {prime 2} 1 {prime 3} 1 {prime 4} 0 {prime 5} 1 {prime 6} 0 {prime 7} 1
test {flipper 2} -2 {flipper -5} 5 {flipper 111} -111 {flipper 1} -1
test {kzero 2 } 2 {kzero -5 } -5 {kzero 0 } .0000001 {kzero 5 } 5
}
# Following McCarthy's notation, use from RS
# shorter symbolic names for the two basic functions:
proc ' { x } {incr x}
# test {' 0} 1 {' 42} 43
proc = {m n} {string equal $m $n}
# RS main deck
proc succ { x } {incr x}
# equality of integers in canonical form can,
# without using expr, be had as
proc eq {m n} {string equal $m $n}
# proc eq works with strings and numbers
# McCarthy advocates "conditional expressions",
# alternating sequences of {condition} {result} like
# A B C D ...
# which can in Tcl (and many other languages)
# be implemented as variables & conditionals
# if $A then $B elseif $C then $D ...
# or more compactly with expr's ?: ternary operator:
# $A? $B: $C? $D: ...
# using expr in these experiments only for the ?: operator
# before Playing Recursion deck
# Following McCarthy's notation, use -RS
# shorter symbolic names for the two basic functions:
proc ' { x } {incr x}
# test {' 0} 1 {' 42} 43
proc = {m n} {string equal $m $n}
# test {= 0 0} 1 {= 0 42} 0 {= 42 42} 1
# The partial converse of the successor function is the predecessor
# "the non-negative integer before"),
# where the auxiliary function pred2 uses recursion
# - it calls itself (as most of the following will).
# The next definitions are a mechanical
# transcription to Tcl of McCarthy's:
func pred { n } {[pred2 $n 0]}
func pred2 {n m} {[= [' $m] $n]? $m: [pred2 $n [' $m]]}
# test {pred 42} 41 {pred 1} 0
#-- This allows us to define the sum:
func + {m n} {[= $n 0]? $m: [+ [' $m] [pred $n]]}
# test {+ 3 4} 7
#-- the product
func * {m n} {[= $n 0]? 0: [+ $m [* $m [pred $n]]]}
# test {* 3 4} 12
#-- the difference (defined only for m >= n)
func - {m n} {[= $n 0]? $m: [- [pred $m] [pred $n]]}
# test {- 12 7} 5 {- 1 1} 0 {- 0 0} 0
#-- the inequality predicate <=
func <= {m n} {[= $m 0]? 1: [= $n 0]? 0: [<= [pred $m] [pred $n]]}
# test {<= 1 2} 1 {<= 2 2} 1 {<= 3 2} 0
#-- leading to the strict inequality <
func < {m n} {[= $m $n]? 0: [<= $m $n]}
# test {< 1 2} 1 {< 2 2} 0 {< 3 2} 0
#-- Integer division goes like this:
func / {m n} {[< $m $n]? 0: [' [/ [- $m $n] $n]]}
# test {/ 1 2} 0 {/ 2 2} 1 {/ 3 2} 1 {/ 42 2} 21
#-- Integer division remainder (% in expr)
func rem {m n} {[< $m $n]? $m: [rem [- $m $n] $n]}
# test {rem 1 2} 1 {rem 2 2} 0 {rem 3 2} 1
#-- Divisibility of a number n by a number m
func | {m n} {[= $n 0]? 1: [< $n $m]? 0: [| $m [- $n $m]]}
# test {| 2 42} 1 {| 2 43} 0 {| 2 3} 0
# Primeness of a number uses another auxiliary helper function.
func prime { n } {[= $n 0]? 0: [= $n 1]? 0: [prime2 $n 2]}
func prime2 {m n} {[= $m $n]? 1: [| $n $m]? 0: [prime2 $m [' $n]]}
# test {prime 2} 1 {prime 3} 1 {prime 4} 0 {prime 5} 1 {prime 6} 0 {prime 7} 1
#-- Greatest common denominator, according to Euclid's algorithm:
func gcd {m n} {[<= $n $m]? [gcd $n $m]:
[= [rem $n $m] 0]? $m:
[gcd [rem $n $m] $m] }
# **********Extensions from gold **********
# Suggest maintain air gaps, dead spaces, brackets
proc IsOdd { N } { return [ expr {$N % 2} ] }
proc IsEven { N } { return [ expr { ( $N + 1 ) % 2} ] }
proc IsNegative { x } { return [ expr {$x<0}]}
proc IsPositive { x } {return [ expr {$x>0}]}
#-- >= greater than or equal to logic function
func >= {m n} {[= $n 0]? 1: [= $m 0]? 0: [>= [pred $m] [pred $n]]}
#-- > greater than logic function
func > {m n} {[= $m $n]? 0: [>= $m $n]}
# proc kzero { n } { return [expr $n ] }
func kzero { n } {[= $n 0]? 0.0000001: [= $n 0.]? 0.0000001: $n }
proc flipper { n } { return [expr {$n * -1 } ] }
# func abs { n } {[< $n 0]? $n:[ flipper $n } ]}
proc sgn { x } {expr {($x>0) - ($x<0)}
#-- triangular number. Tricky code
# and Suggest maintain air gaps, spaces, brackets
func tri { n } {[< $n 2]? 1: [/ [* $n [+ $n 1] ] 2 ]}
# test {tri 3} 6 {tri 2} 3 {tri 5} 15
#-- factorial recursion, but quickly exceeds domain
# fac is recursion limited, & excessive time beyond factorial 7
func fac { n } {$n<2? 1: [* $n [fac [pred $n ]]]}
#-- min, max, basic integer funcions
# but may need some error checks
# for entry zeros and equality, $m = $n
func min {m n} {$m<$n? $m: $n}
func max {m n} {$m>$n? $m: $n}
# zero_killer function swaps points of zero
# for 0.0000001 in observed data to avoid
# computer division by zero
# testing funcs here
# func kzero { n } {[= $n 0]? 0.0000001: [= $n 0.]? 0.0000001: $n }
# func kzero { n } { return $n }
# computer division by zero
# ******* end extensions ************
# critical bracket end of namespace, must be present
}
# but if gone, hard to spot from dire consequences
# yada yada inside namespace ::liner:: =}
# after Playing Recursion deck
proc !! {} {info commands ::liner::* }
proc $$ {} {puts " namespace ::liner:: activated , info commands is !! " }
proc && {} {puts " namespace ::liner::demo activated " ; ::liner::demo }
puts " ***** enter to invoke namespace ::liner::* or $$ "
puts " ***** enter liner::func_name to invoke single func ********** "
puts " ***** list cmds with info commands ::liner::* or !! "
puts " ***** enter liner::demo for code test *** or && "
puts " ******* but considerable lengthy recursions **** "
puts " ***** Self_Help under Help button of ActiveTcl Console *** "
console show
console eval {.console config -bg palegreen}
console eval {.console config -font {fixed 20 bold}}
console eval {wm geometry . 40x20}
console eval {wm title . " Playing with Recursion V2, screen grab and paste from console 2 to texteditor"}
console eval {. configure -background orange -highlightcolor brown -relief raised -border 30}
console eval { proc self_helpx {} {
set msg "in TCL, large black type on green
from TCL Wiki,
self help listing
Conventional text editor formulas grabbed
from internet screens can be pasted
into green console
# testbed & demo_recursion_functional_programming
# demo command is demo
# suggest maintain dead spaces and air gaps
# near expr, brackets, etc in following statements
# written on Windows 10 on TCL
# working under TCL version 8.6
# gold on TCL Club , 05ct2020
# easy eye console has large black type on green
# used as testbed for integer arithmetic
# Playing with Recursion V2
# Playing with Recursion is TCL wiki page
# < positive integers > function procs written by RS
# gold added cosmetics
# some extension funcs and procs experiment with reals
# equality of integers in canonical form can,
# without using expr, be written
# proc eq is TCL string function
# McCarthy advocates <conditional expressions>,
# alternating sequences of {condition} {result}
# which can in Tcl (and many other languages)
# be implemented as variables & conditionals
# if \$\A then \$\B elseif \$\C then \$\D ...
# or more compactly with expr's ?: ternary operator:
# \$\A\? \$\B\: \$\C\? \$\D\: ...
# using expr in these experiments only
# for the ?: operator
# The partial converse of the successor function is the predecessor
# the non-negative integer before,
# where the auxiliary function pred2 uses recursion
# meaning it calls itself (as many here will).
# There's a tiny multi-case tester: from RS
# after Playing Recursion deck
# proc !! info commands ::liner::*
# proc $$ puts namespace ::liner:: activated ,
# info commands is !!
# proc && puts namespace ::liner::demo activated
# ; ::liner::demo
# list cmds with < info commands ::liner::* > or !!
# \demo added puts result to original proc test1
# demo integer functions from RS, TCL Wiki "
tk_messageBox -title "self_helpxx" -message $msg } }
console eval {.menubar.help add command -label Self_Help -command self_helpx }
# Disclaimers: 10/01/2020
# end of fileTesting Additional Functions
gold 9/25/2021 update pending
# written on Windows 10 in ActiveTCL
# working under TCL version 8.6
# gold on TCL Club , 25sep2021
package require math::numtheory
package require math::constants
package require math
namespace path {::tcl::mathop ::tcl::mathfunc math::numtheory math::constants }
# Tcllib:math paths to compare timings inside Tcllib and namespace liner
# logic tests for even, odd, positive, negative, conditions of positive numbers
# uses logic inside expr , if positive return 1, if not positive return 0
proc isPositive { n } {return [ expr {$n > 0}]}
# Richard Suchenwirth RS idea in Math Sugar
# uses logic inside expr, if negative return 1, if not negative return 0
proc isNegative { n } { return [ expr {$n < 0}]}
# Richard Suchenwirth RS idea from wiki: Math Sugar
# No error traps or safety nets here for negative and real numbers.
# conditional proc IsOdd, if N odd, return 1, if N not odd, return 0.
proc IsOdd { n } { return [ expr {$n % 2} ] }
# Usage
IsOdd 5 ;# returns 1
# conditional proc IsEven, if N even, return 1. If N not even return 0.
proc IsEven { n } { return [ expr { ( $n + 1 ) % 2} ] }
# IsEven 4 ;# returns 1
# following functions used in namespace liner
func isPositive {n] { $n>0? 1: 0 }
func isNegative {n} { $n<0? 1: 0 }
func isOdd {n} { ( $n % 2 ) ? 1: 0 }
func isEven {n} { ( $n % 2 ) ? 0: 1 }
# liner::isNegative 5 ;# returns 0
# liner::isNegative -5 ;# returns 1
# liner::isOdd 5 ;# returns 1
# liner::isOdd 4 ;# returns 0
# liner::isEven 4 ;# returns 1
# liner::isEven 5 ;# returns 0
Console Program for step_function Table
;# pretty print from autoindent and ased editor
;# step_function_table V2
;# testbed for One Liners Program
;# written on Windows 10 on Tcl 8.6
;# working under Tcl version 8.6
;# gold on Tcl Club , 2020-10-18
;# Ref. WIKI BOOKS, Tcl_Programming_Introduction
;# Book Section contrasts one liners program
;# versus traditional procedural approach
;# below contains redundant procs
package require Tk
package require math::numtheory
package require math::constants
package require math::trig
package require math
namespace path {::tcl::mathop ::tcl::mathfunc math::numtheory math::trig math::constants }
;# set tcl_precision 17
set tcl_precision 3
proc pie {} {return [expr acos(-1)]}
console show
console eval {.console config -bg palegreen}
console eval {.console config -font {fixed 20 bold}}
console eval {wm geometry . 40x20}
;# model if procedure from RS derived
;# for conditional if_elseif_else statement
;# reasonably fast too for Tcl script
;# merely string text assignments,
;# no extra math calculation after then
;# from Modeling COND with expr on Tcl Wiki
;# alternates after then is either return $sgn ,
;# return 1 , or return 0
;# vis set statement
proc model_proc_sgn nn {
# standard multi-test if from RS derived
if {$nn>0} {
set sgn 1
} elseif {$nn<0} {
set sgn -1
} else {
set sgn 0
}
;# one liner program step_function on extended line
proc step_function nn { if {$nn<-1} { return 0 } elseif {$nn<0 } /
{ return 1 } elseif {$nn==0} { return 1 } elseif { $nn<1} /
{ return 1 } elseif {$nn>1 } { return 0 } else { return 0 }}
set limit 20
puts "%|table| | printed in|Tcl format |% "
puts "&| session| proc & mean value| comment, if any|& "
for { set i -10 } { $i <= $limit } { incr i } {
;# set lister { 1 2 4 5 6 7 8 9 10 }
;# lappend lister [* $i [pie]]
puts "&| [* $i .2 ] |step_function [ step_function [* $i .2 ] ] | |&"
}
;# end of file Console Program, lines reduced for test of namespace
gold 10/10/2021 updated. Note: Namespace has to have mathop and mathfunc installed for some functions and procs to work inside namespace.
gold Notes. The average of sequence < 7 11 13 14 > was expr { (7 + 11+13+14)/4 }, 11. The harmonic mean of sequence < 7 11 13 14 > was expr { 4/(1./7 + 1./11 +1./13 +1./14 ) }, 10.46797385620915. The harmonic mean of sequence < 7 11 13 14 > was expr { 4/(1./7 + 1./11 +1./13 +1./14 ) }, 10.46797385620915. The Babylonian fraction method was expr { (7/60. + 11/60.+13/60.+14/60.)/4. }, 0.1875. The Babylonian fraction method was equivalent to expr {0.1875*60. } to 11.25/60. The Babylonian fraction method was expr { (7/60. + 11/60.+13/60.+14/60.)/4. }, 0.1875. The Babylonian fraction method was equivalent to expr {0.1875*60. } to 11.25/60.
# gold on TCL Club , 05ct2020
# console has large black type on green
# used as testbed for integer arithmetic
# Test namespace player for Recursion V2 ???
# lines reduced for test of namespace
# Playing with Recursion is TCL wiki page by RS
# < positive integers > function procs written by RS
# gold added cosmetics in console deck
package require Tk
package require math::numtheory
package require math::constants
package require math::trig
package require math
namespace path {::tcl::mathop ::tcl::mathfunc math::numtheory math::trig math::constants }
namespace path {::tcl::mathop ::tcl::mathfunc}
set tclprecision 17
proc func {name argl body} {proc $name $argl [list expr $body]}
# func tri { n } {[< $n 2]? 1: [/ [* $n [+ $n 1] ] 2 ]}
# proc func {name argl body} {proc $name $argl [list expr $body]}
func tri { n } {[< $n 2]? 1: [/ [* $n [+ $n 1] ] 2 ]}
puts " ****** begin namespace player 1 ******** "
# begin namespace player
namespace eval player {
namespace export math
package require Tk
# Note: Namespace has to have mathop and mathfunc
# installed for some functions and procs to work.
namespace path {::tcl::mathop ::tcl::mathfunc}
puts " ****** begin namespace player 2 ******** "
proc func {name argl body} {proc $name $argl [list expr $body]}
func tri { n } {[< $n 2]? 1: [/ [* $n [+ $n 1] ] 2 ]}
# end bracket for namespace player
}
# end bracket for namespace player
console show
set rrr [ tri 5 ]
puts " check player [ tri 5 ] "
puts " check player [ player::tri 5 ] "Hidden Comments Section
** Hidden Comments Section **
Please place any comments here with your moniker, Thanks. gold 11/2/2020. expr sqrt ( 1.618033988749895**2 - .618033988749895*2.) -> 1.175570504584946 ref 1.2 factor in steve's formula.
test! seems to work
gold10/25/2020. Reloaded version 102 proof of PYK, page was overwritten, omitting items as requested.
gold 10/27/2020. Typos, added positive step function, added tables with some figures. Did not want to break up prose more or type in too much inside "proofed" prose
gold 10/28/2020. added namespace paragraph, added namespace session. added several new funcs.
gold 10/28/2020. added testcase 4 for phi and testcase 5 for pi approximation
gold 11/08/2020. added pi math references, added TCLLIB integration of pi
gold 11/13/2020. added Table for McCarthy Logic and Table of Procs and funcs.
gold 11/20/2020. added Triangular Number Multiplication.
gold 9/27/2021. Switched some comment signs ;# to #. This a big file. Check earlier editions, if not compatible. Maybe obvious, but this page was written on Windows10 Tcl ports including ActiveTCL and has dependencies on same. I assume reader can cut and paste, what the reader needs, and tootle on to his own project and own important contribution pages to the TCL Wiki.
| Category Numerical Analysis | Category Toys | Category Calculator | Category Mathematics | Category Example | Toys and Games | Category Games | Category Application | Category GUI |