Trig Procedures for degree measures as sind, cosd, tand,etc
Trig Procedures for degree measures as sind, cosd, tand,etc
This page is under development. Comments are welcome, but please load any comments in the comments section at the bottom of the page. Please include your wiki MONIKER and date in your comment with the same courtesy that I will give you. Aside from your courtesy, your wiki MONIKER and date as a signature and minimal good faith of any internet post are the rules of this TCL-WIKI. Its very hard to reply reasonably without some background of the correspondent on his WIKI bio page. Thanks,gold,12DEC2018
- Trig Procedures for degree measures as sind, cosd, tand,etc
- Pseudocode Section
- Appendix Code
- appendix TCL programs and scripts
- Testbed Calculator with fixed testcases and some Pade_trig subroutines
- Alternate subroutines under test
- Range aware switch from ranged switch
- Test with angle intervals of 90 degrees
- "Umut Tech fast sine algorithm" into TCL on the TCL/wiki
- Test with angle intervals of 10 degrees
- Comments Section
gold Here is some TCL starter code for Trig Procedures using degree measures as sind, cosd, tand, etc. Recognize these trig functions (with radian measures) are convertible with your degToRad and radToDeg math::constants in the TCLLIB, but the usual trigonometric functions with input values as scalar or vector in degrees might be convenient to some users. Npte: Some tickets are closed and functions available in Tcllib. Many thanks to arjen & Andreas Kupries for the heavy lifting.
In planning any software, it is advisable to gather a number of testcases to check the results of the program. Here, a TCL slot calculator is being used as a testbed for trig procedures. The results of the testcases are estimated using the hand calculator and then checked in the slot calculator. Pseudocode and equations are developed from the hand calculations and theory. Small console programs are written to check or proof the alternate subroutines or procedures, rather than keeping the unblessed code and comment lines in the main slot calculator. Finally the improved or alternate subroutines are loaded into the slot calculator. The TCL slot calculator is effectively a shell program to input entries, retain loaded standard testcases, host calculation routines, and display results. Additional significant figures are used to check the TCL calculator, not to infer the accuracy of inputs and product reports.
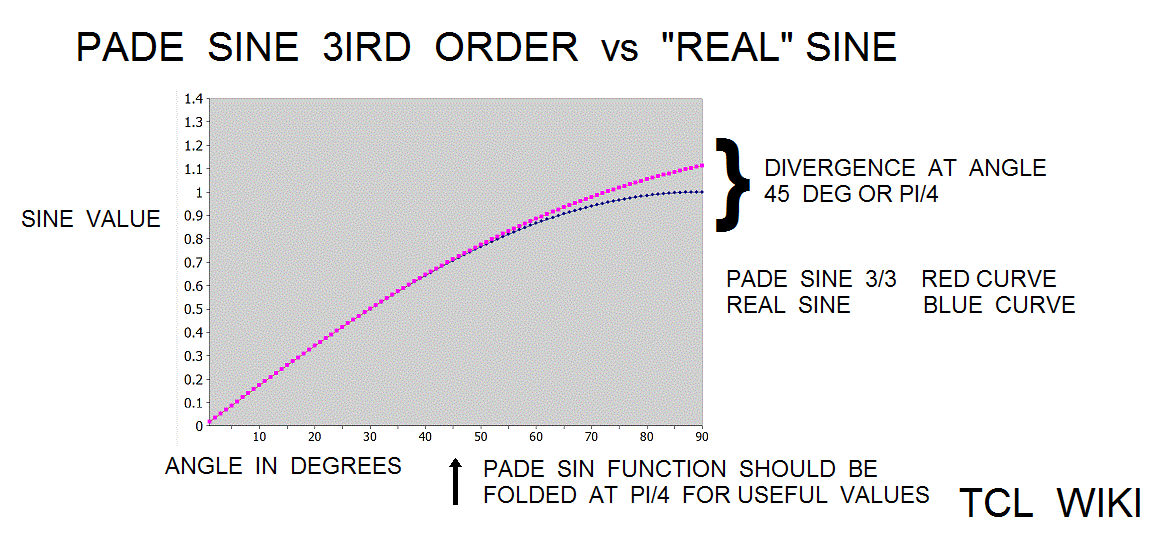
The testbed is mostly using Padé trig functions, but it is clear that the Padé trig functions are accurate only at small angles. The calculator needs an angle reduction system, switch, or ranged switch installed. Pade' or Padé is a French mathematician with an accent, but pade as ASCII is used from the variables here. ----.
Important Note. Not a Replacement
gold 7/5/2021 update. Important Note. See note from arjen below. See better routines and current methods for angle reduction, sin, cos, etc in the TCL core distribution and TCLLIB. This page were largely developed under the earlier TCL4, ETCL, and TCL8.~~ versions on an outdated personal computer. This page is not a replacement for the current TCL core and TCLLIB with much improvement since TCL4 and other <faster> language constructs. See better routines and current methods for angle reduction, sin, cos, pi, etc in the TCL core distribution and TCLLIB. As of Jul2018, the TCLLIB has developed code for trig angles in degrees, trig inverse, and hyper functions in degrees, and angle reduction in radians and degrees. This supplemental trig.tcl, trigtest.tcl, and trig.man code is posted on the TCLLIB website. This math::trig.tcl seems really exciting work, which will keep TCL in pace with some of the other brand name languages (math oriented, I mean). Some of the TCL library code is posted as pending on the TCLLIB website, and sometimes not really in the main TCL distribution yet, so its worthwhile to investigate and run searches on the pending TCLLIB code, the SourceForge bins, and [L1 ] locations also. The TCLLIB math library is generally quicker and more accurate by a third over some homebrew code, see math::mean , Additional math functions, [L2 ]. The numerous examples on this wiki page include code lines that might be incompatible, inefficient, dead_weights, or redundant if installed in the same program. As discussed below, the local math procedures in scripts and one-line procedures may not be as fast and efficient as importing mathop , mathfunc, and math from TCLLIB and SourceForge, so check with the precompiled code in the TCL core and TCLLIB libraries >> first <<, then homebrew your one liners programs and scripts in TCL.
Angle reduction
Based on intervals of pi/4 or pi/N, there are several angle reduction algorithms under consideration. Angle $aa below pi/4 would have no correction needed. Angle $aa below -180 or above 180 degrees could be corrected by substitution table. Angle $aa below -360 or above 360 degrees could be partially corrected by available procedure and then reduced by other techniques. The algorithm for large angles (>> pi/4) known locally as the sin+cos angle sum algorithm has been implemented in C++ and Sparc fortran, but seems complex for the proposed TCL implementation.
Avenues for better accuracy
Avenues for better accuracy. Because the accuracy of the Pade trig functions degrade away from the origin point of computation, then the evaluation of the Pade trig functions should be restricted to the interval -(pi/4) to +(pi/4) for better accuracy. Mostly the Pade functions in the monographs are computed near the conventional origin (0,0), but moving the computation point of the Pade function near the evaluation interval of the specific angle is conceivable. The paper math to move the computation point would be heavy, but possibly a computation algorithm would be possible. The Pade function evaluation is generally a thousand or thousands of times more accurate in the interval near the origin point of computation. Since the trig functions are periodic and wrap around, subtracting +- 360 degrees from angles outside the -+360 degree interval would be a partial solution. Multiplication by 1/(2.*pi) or 1/(360) would reduce an angle inside the -+360 degree interval to inside the -+(pi/4). Then the double angle theorem or power angle theorem could be used to find the transform of the specific angle, ref monograph by Mendenhall.
Using Pade_ln(1+x) 720 as an analogy for a trig function, precede with multiplication 720*(1./360.) = 2.0. The third order Pade function would evaluate as Pade_ln_1_x(720) as` 3.6336653842253304, showing substantial error due to distance from the computation origin. The TCL_eval ( log 720) gives 6.579251212010101. The relative error was expr (6.5792-3.6336)/-3.6336) or 81 percent. 0.693121693121693. Closer to the computation origin, the Pade_ln_1_x(2 ) gives 0.693121693121693. The TCL_eval ( log 2) gives 0.6931471805599453. Near the computation origin, the relative error was expr (0.69314718-0.69312169)/0.69312169 , 3.67E-5. For the example of the Pade_ln, the relative error was .81/3.67E-5 or 2.2E4 greater distant from the function computation point. If the general solution ln(a*b) = ln(a) + ln(b) is used as a sort of transform, then ln(2*(360.)) = ln(2)+ln(360.). Adding Ln(360.) to Pade_ln(2) would give 5.886104031450156 + 0.693121693121693 as transform 6.579225724571849. An error would still be present as (6.579225724571849-6.579251212010101)/ 6.579251212010101 or error of 3.87e-6. Also, ln 360. or 5.8 can be treated as constant or fixed number in subroutine, rather than evaluated each time. An all Pade_ln would be possible eval ln(360.) as the sum of the Pade_ln for each small prime factor of 360 (2, 2, 2, 3, 3, 5). The all Pade_ln solution would be Pade_ln(2) + Pade_ln(2,2,2,3,3,5) as 6.747276688453158. The error from the TCL eval (log 720) would be expr (6.747276688453158-6.579251212010101)/6.579251212010101 or 2.5 percent error. Not sure about the exact antidotal numbers, but finding the Pade solution near the function computation point (usually 0,0) and transforming the solution to a more distant region seems possible.
Of course, the snag in small angle theory is that sin(n*x) =! n*sin(x), so sin(x) can be calculated as a small angle and then a transform must be used. The algorithm for large angles (>> pi/4) known locally as the sin+cos angle sum algorithm has been implemented in C++ and Sparc fortran. The c++ strategy in Umut's tech-blog seems fast and understandable to implement using the sin+cos angle sum. The essential strategy is breaking an angle into the sum of a large angle and small angle, then using small angle theory to find sin (and cos) of the small angle and then transforming the small angle solution into the region of the original combined angle, angle sum formula. The sin and cos components of the large angle at 10 degree intervals can be stored in tables for the transform.
A similar strategy may be undertaken with the sin and cos recurrence formula as sin(n*x)=2*sin((n-1)*x)*cos(x) - sin ((n-2)*x). Subbing 361 for n, sin(361*x)=2*sin((361-1)*x)*cos(x) - sin ((361-2)*x) and reduction of terms, sin(361*x)=2*sin((360)*x)*cos x - sin ((360-1)*x). Since sin(360*x) is equivalent to sin(x), then sin(361*x)=2*sin(x)*cos (x) - sin ((360-1)*x). A small angle called alpha from original x, alpha=x*(1./361.). Since there will be some inaccuracy from the small angle theory, the TCL script procedure can probably use the approximations alpha=x*(1./361.);sin(361*alpha)=~~ 2*sin(alpha)*cos (alpha) - sin (alpha). Hence the small angle approximations for both sin (alpha) and cos (alpha) are loaded into procs. When the sin and cos recurrence code is more confident, then pade_trig procs could replace the small angle procs.
Changes for Timing
This paragraph is intended to show peg points or improvements as the TCL coding progressed. I don't have all the details on the C++ coding & machines, but Umut's fast sine is about 30 to 65 ticks on his machine. Another C++ coder reported 140 to 320 ticks for various sin algorithms with much interpolation, folding pi/2 sections, and error checking. For the TCL coding and using table constants only without the trig functions, the sin*cos statement is rated 1.24 microseconds per iteration. The sin*cos with TCL math.c derived sin and cos functions only (no pade sin and cos) was rated as 60 microseconds per iteration in the first trial. The pade sin with expr was rated as 43 microseconds per iteration. The pade sin and pade cos were changed from expr to operator math. The pade sin with operator notation was rated at 38 microseconds per iteration. After several TCL code changes, the umut_tech_fast_sind timing was 33.311 microseconds per iteration. In the umut_tech_fast_sind subroutine, there are two function calls to pade_sin and pade_cos that account for the bulk of the time. For comparison, the tcl sine derived and alone was 3.862 microseconds per iteration. Since the pade_sin and pade_cos are used for x << pi/2 and Umut's table was limited to 100 degrees, umut_tech_fast_sind reverts to the less accurate pade_sin alone (no tables nor sin*cos transform) after 100 degrees. The angle_reduction_degrees, pade_sin, and pade_cos subroutines were tested and worked in the local copy of TCLLIB, but there is about 25 microseconds of overhead that is uncertain.
Kurweg_Timmins_Legendre_quotient subroutines
The Kurweig Timmins Legendre quotient subroutines were accurate to 13 places and timing was about 15.5 microseconds per iteration (KTL_tand). The KTL_cosd formula was more involved and was about 17.6 microseconds per iteration. It is believed that the Kurweig-Timmins quotient subroutines would benefit from folding subroutines to the pi/2 interval. The Kurweig-Timmins quotient subroutines in TCL coding are about 5 times slower than the TCL invoked sine using the math.h library (C or C++}. In more detail, the formula for the Kurweg_Timmins_Legendre_atand was written for 1/a and the original formula is accurate for a >> 5. The KTL_atand calculations with a < 1 need transform or substitution <pi/2-atan a>. The KTL_atand was about 14.8 microseconds per iteration.
Summary on Pade_trig status
gold, 30Dec2017. The calculator testbed posted on the TCL-wiki is mostly using Padé trig functions, but it is clear that the Padé trig functions are accurate only at small angles. The calculator needs an angle reduction system and ranged switch installed. Pade' or Padé is a French mathematician with an accent, but Pade_trig as ASCII is used from the Tool Control Language variables here.
30dec2017. A sample Sagemath script will generate nested (horner) expressions and pade quotients in different orders for the trig. functions. I don't have complete resources to check the pade quotient outputs, but maybe (we) can help compile a reference table for the next seeker. Meaning that the table of Taylor and Pade trig functions should be compatible with the TCLLIB::math::polynomial library. My tcl program is limited to effective double precision, 17 s. figures, so I'll stop somewhat short of Pade orders 9/9, when constants exceed tcl_precision 17.
Pseudocode Section
# using pseudocode for procedure algorithm.
3 quantities needed
angle a in radians. Multiply by pi/180 to convert degrees to radians.
a in radians
package require math::constants
radtodeg = 57.295779513100001 = Conversion from radians to degrees
degtorad = 0.017453292519943001 = Conversion from degrees to radians
set con5 $math::constants::degtorad
set con6 $math::constants::radtodeg
invoke 0.017453292519943001
set a [* $a (3.14/180) ] , 3.14/180~0.01744
set a [sin $a ]
return $a
sind = sin(0.174 * x), fortran 90
sin = sin(op)
cos = cos(op)
tan = tan(op)
sind = sin(op*(PI/180.0))
cosd = cos(op*(PI/180.0))
tand = tan(op*(PI/180.0))
poss. sin(x) =
x^1/1! – x^3/3! + x^5/5! – x^7/7! + x^9/9! series, ref Matlab
poss. cos(x) =
1 – x^2/2! + x^4/4! series, ref Matlab
poss. sind=sin(x*Pi/180) =
x*Pi/180 -(x*Pi/180)^3/3! + (x*Pi/180)^5/5! series, ref Matlab
proc sind {aa} {set aa [* $aa $math::constants::degtorad ];return [sin $aa ]}
check function in TCL
ref. number format procedure
check_answer new area =? desired goal , desired goal reached (yes/no)
set answers and printout with resulting values
cos table from Chebyshev approximation , console show; puts " $ctable "
in table subroutine.Testcases Section
In planning any software, it is advisable to gather a number of testcases to check the results of the program. The math for the testcases can be checked by pasting statements in the TCL console.
Testcase 1
| table 2 | printed in | tcl wiki format |
|---|---|---|
| quantity | value | comment, if any |
| 2: | testcase_number | |
| 45.0 : | degrees | |
| 0.78539816339743507 : | answers : conv. radians, used in arc functions | |
| 0.70710343676668519 : | cosd function | |
| 0.99978768091494197 : | tand function | |
| 1.0002123641740253 : | cotd function | |
| 1.4142202512444562 : | secd function | |
| 1.4142202512444562 : | cscd function | |
| 0.70710678118653814 : | sind function | |
| 45.000000000013131 : | asind function | |
| 45.000000000013131 : | acosd function | |
| 45.000000000013131: | atand function | |
| 45.000000000013131: | acotd function | |
| 1.0000939590259186: | asecd function | |
| 45.000000000013131 : | acscd function |
pi = 3.1415926535897931 = ratio of circle circumference and diameter e = 2.7182818284590451 = base for natural logarithm radtodeg = 57.295779513100001 = Conversion from radians to degrees degtorad = 0.017453292519943001 = Conversion from degrees to radians
Testcase 2
| table 2 | printed in | tcl wiki format |
|---|---|---|
| quantity | value | comment, if any |
| 2: | testcase_number | |
| 180.0 : | degrees | |
| 0.86599999999999999 : | radians | |
| -1.0 : | cosd function | |
| -5.2969080652072186e-14 : | tand function | diff. residual |
| 5.2969080652072186e-14 : | sind function | diff. residual |
Testcase 3
| table 3 | printed in | tcl wiki format |
|---|---|---|
| quantity | value | comment, if any |
| 3: | testcase_number | |
| 270.0 : | degrees | |
| 0.70699999999999996 : | radians | |
| -8.0119754792883374e-14 : | cosd function | diff. residual |
| undefined: | tand function | diff. residual |
| -1.0 : | sind function |
| table 4 | printed in | tcl wiki format |
|---|---|---|
| quantity | value | comment, if any |
| 3: | testcase_number | |
| 360.0 : | degrees | |
| 0.94999999999999996 : | radians | |
| 1.0 : | cosd function | |
| -1.0593816130414437e-13 : | tand function | diff. residual |
| -1.0593816130414437e-13 : | sind function | diff. residual |
References:
- Henri Padé, French mathematician, Wikipedia
- Practical Numeric Math Functions, Pracma package,
- R-language (GNU S), 21Nov2017, Hans w. Borchers,
- includes acosd, acot, acotd, acsc, acscd,
- asec, asecd, asind, atand, atan2d,
- cosd, cot, cotd, csc, cscd, includes Pracma.pdf manual
- Apparently, the E-console can invoke a tk/tcl library
- and/or commands in tcl/bin to the Pragma library
- Pade package distributed in R-language library,
- includes Pade.pdf manual
- Attachment "extrafuncs.tcl" to ticket No. 641143ffff
- added by dkf on 2006-03-16 16:27:34.
- Pade approximants for inverse trigonometric functions
- and their applications, Shanhe Wu and Gabriel Bercu,
- key paper on Pade trig.
- sin
- Maxima
- Chebyshev approximation
- get cos table from Chebyshev approximation,
- TCL > console show; puts " $ctable "
- Evaluating polynomial functions
- a tcl script for function value listing based on a fortran expression
- SQLite has cot?
- Sine of argument in degrees - MATLAB sind, de.mathworks.com
- degrees - MATLAB sin() vs sind() , Stack Overflow, stackoverflow.com
- For integers n , sind(n*180) is exactly zero, whereas sin(n*pi)
- Trigonometry Formulas , Math Is Fun Forum
- Python: converting radians to degrees,Stack Overflow, stackoverflow.com
- C mathematical functions, From Wikipedia, the free encyclopedia
- Aircraft Trajectory Modeling and Alerting Algorithm,
- modeling sind (fm f77) etc
- with series, feel safe in the cockpit?
- Computer Approximations,Hart and Cheney,
- Ref. Chebyshev Polynomials.
- Elementary Functions. Algorithms and Implementation},
- Jean-Michel Muller, 2016
- NIST, online library of digital functions, inverse series
- Y. L. Luke (1975) Mathematical Functions and their Approximations.
- Academic Press Inc., New York.
- Padé Approximants,George A. Baker, Peter Graves-Morris
- Pade approximants for inverse trigonometric functions and their applications,
- Shanhe Wu and Gabriel Bercu
- George A. Baker Essentials of Pade approximants
- Academic Press 1975
- Della Dora J. Approximation de fonctions complexe au sens
- Hermite-Pade et Hardy, PhD Thesis ed., 1980 in French
- C. Brezinski Continued fractions and Pade approximants
- North-Holland, 1990 , English
- Claude Brezinski (auth.) Springer Series in Computational Mathematics 12
- History of Continued Fractions and Padé Approximants 1st ed.
- Springer-Verlag Berlin Heidelberg, 1991,English
- P.R.Graves- Morris Pade approximants and their applications Proc Kent
- Academic Press Inc ,English
- Baker G.A., et al. Collection of reviews and papers
- on convergence of Pade approximants Kluwer, 1999 , English
- George A. Baker Jr., John L. Gammel The Pade approximant in theoretical physics
- Elsevier Science , 1970 , English
- H. Cabannes, LNP0047
- Pade Approximants Method and Its Applications to Mechanics ,1 ed.
- Springer, 1976, English
- E.B. Safe (Eds.) Pade and Rational Approximation. Theory and Applications
- Academic Press 1977 English
- Springer International Publishing 2014 , English
- George A Baker Section, Mathematics of physics ,v. 1
- Pade approximants, Addison-Wesley, Advanced Book Program 1981 English
- George A Baker Section,
- Mathematics of physics, v. 1
- Pade approximants
- Addison-Wesley, Advanced Book Program , 1981 , English
- Jochen Pade Undergraduate Lecture Notes in Physics
- Quantum Mechanics for Pedestrians 2: Applications and Extensions ,2014 ed.,
- Guo,B,Wang,R,Xu,M: Padé approximation of sine functions and its application in numerical
- analysis. J.Inf.Comput. Sci.12(15),5545-5550(2015)
- Bercu,G:Padé approximant related to remarkable inequalities involving
- trigonometric functions.J.Inequal.Appl. 2016,ArticleID99(2016)
- Bercu,G,Wu,S: Refinements of certain hyperbolic inequalities via the
- Pade approximation method. J.NonlinearSci. Appl.9(7),5011-5020(2016)
- An approximate analytic inversion of Kepler's equation,
- D. Lynden-Bell, pade_sin used by astronomer to solve Kepler's equation.
- A Fast, Vectorizable Algorithm for Producing Single-Precision Sine-Cosine Pairs
- Marcus H. Mendenhall
- ranged switch
- range
- Umut's tech-blog, Reinventing the wheel : write your own fast sine (c++ code),
- seems fast and understandable to implement.
- On 12/12/2017 received Umut's permission to load the
- "Umut Tech fast sine algorithm" into TCL on the TCL/wiki
- telescoping for $a+$b*$x+$c*$x**2+$d*$x**3 as (($d*x+$c)*$x+$b)*x+$a
- 3 + sin( 3 ) + sin( 3 + sin( 3 ) ) + sin( 3 + sin( 3 ) + sin( 3 + sin( 3 ) ) ) =? pi
- www.boost.org, boost math, c++ library
- search for TCL code on retained open source google code,
- [L3 ]
- other keyword projects >>> label:tcl label:tcllib label:Tk
- search on github.
- search keywords for "faster" trig approximations.
- sin cos tan trig series efficient approximation "nested polynomial" multiplication
- "Horner's method" "Horner's form" recursive telescoping
- Vol. 84, No. 2 (April 2011), pp. 98-107
- Operations on series of numerical data
- Evaluating polynomial functions
- Intel Underestimates Error Bounds ,on fsin
- Posted on October 9, 2014 ,random ascii news
- New Analytic Method to Approximate Trigonometric
- Functions based upon Legendre Polynomials,
- Ulrich H. Kurzweg, Sidney Timmins,IEEE paper
- A new method for obtaining highly accurate
- approximations to the arctan function,
- Ulrich H.Kurzweg and Sidey P.Timmins, 27 Aug 2011
- Pade approximants, Ulrich H.Kurzweg
- Pentium FDIV bug, from Wikipedia, hardware calculations
- Cipra, Barry A. (1995-01-13). How number theory got the best
- of the Pentium chip". Science.
- ref (1/824633702441) * 824633702441 on a 486 machine yields 1.
- But on an uncorrected Pentium, the result is 0.99999999627470902,
- within conventional single precision.
- SageMath, the Sage Mathematics Software System (Sagemath Version 8.1),
- The Sage Developers, 2018, http://www.sagemath.org .
| table 1 | list of proposed Pade_trig functions | printed in | tcl wiki format | |
|---|---|---|---|---|
| designation | definition | inverse | factors | comment, if any |
| sind(x) | Sine of argument in degrees | |||
| cosd(x) | Cosine of argument in degrees | |||
| tand(x) | Tangent of argument in degrees | |||
| cotd(x) | Cotangent of argument in degrees | |||
| asind(x) | returns the inverse sine (sin-1) of the elements of X in degrees | |||
| acosd(x) | returns the inverse cosine (cosin-1) of the elements of X in degrees | |||
| atand(x) | Inverse tangent in degrees | |||
| acotd(x) | Inverse cotangent in degrees | |||
| secd(x) | Secant of argument in degrees | |||
| cscd(x) | Cosecant of argument in degrees | |||
| asecd(x) | Inverse secant in degrees | |||
| acscd(x) | Inverse cosecant in degrees |
Note. For integers n, sind(n*180) is exactly zero in "older non-standard" Fortran library function. Some details on n*180 and pi need to be researched. Different return calculations of sin and sind were flagged in some GNU fortran trials, circa 2016. Proposed Pade_Trig functions probably need angle reduction procedure to interval of 0-(pi/4).
Small Trig Table , in TCL wiki format
| Small Trig Table | printed in TCL wiki format | |||
|---|---|---|---|---|
| Degrees | Radians | cos | sin | tan |
| 0 | 0 | 1 | 0 | 0 |
| 30 | π/6 | sqrt(3)/2 | 1/2 | sqrt(3)/3 |
| 45 | π/4 | sqrt(2)/2 | sqrt(2)/2 | 1 |
| 60 | π/3 | 1/2 | sqrt(3)/2 | sqrt(3) |
| 90 | π/2 | 0 | 1 | undefined |
| 120 | 2π/3 | -1/2 | sqrt(3)/2 | -sqrt(3) |
| 135 | 3π/4 | -sqrt(2)/2 | sqrt(2)/2 | -1 |
| 150 | 5π/6 | -sqrt(3)/2 | 1/2 | -sqrt(3)/3 |
| 180 | π | -1 | 0 | 0 |
| 210 | 7π/6 | -sqrt(3)/2 | -1/2 | sqrt(3)/3 |
| 225 | 5π/4 | -sqrt(2)/2 | -sqrt(2)/2 | 1 |
| 240 | 4π/3 | -1/2 | -sqrt(3)/2 | sqrt(3) |
| 270 | 3π/2 | 0 | -1 | undefined |
| 300 | 5π/3 | 1/2 | -sqrt(3)/2 | -sqrt(3) |
| 315 | 7π/4 | sqrt(2)/2 | -sqrt(2)/2 | -1 |
| 330 | 11π/6 | sqrt(3)/2 | -1/2 | -sqrt(3)/3 |
Subroutine timing trials
"Umut Tech fast sine algorithm" on the TCL/wiki
| trials timing table 1 | printed in | tcl wiki format |
|---|---|---|
| 1: | testcase_number | |
| quantity | value | comment, if any |
| umut_fast_sind timing, load big num constant | 0.52 microseconds per iteration | |
| umut_fast_sind load cos_table | 0.54 microseconds per iteration | |
| umut_fast_sind timing, degree reduction | 0.33 microseconds per iteration | operator math |
| umut_fast_sind timing, sin*cos comp. | 16.78 microseconds per iteration | operator math |
| umut_fast_sind timing, puts result t1 | 5529 microseconds per iteration | |
| umut_fast_sind timing, puts result t2 | 9689 microseconds per iteration | |
| umut_fast_sind timing, puts result t2 | 9719 microseconds per iteration | |
| umut_fast_sind timing, tcl sine derived (alone) | 26 microseconds per iteration | |
| umut_fast_sind timing, pade sin alone, acc.<<<pi/2 | 43 microseconds per iteration | used expr |
| umut_fast_sind | 0.9491730823827724 | looks too good? acc. attrib. to lookup table |
| output tcl sine derived (alone) | 0.9491730823827661 | |
| printout big num | 3.141592653589793238462643383279502884197169399375105820 | |
| output | pade sin alone , ac <<< pi/2 r 0.9491332939508036 | used expr |
Pitfalls in trig math approximation (+-*/), buzzword collection
| table | Pitfalls in trig math approximation (+-*/), ref. Taylor series esp. | printed in | tcl wiki format | ||
|---|---|---|---|---|---|
| quantity | terms | polynomial or order (x**N) | region (-+n*pi/2) | absolute error of function | comment, if any |
| truncation errors | 3t | sind(45) | 0.707 | may exceed sum of all retained terms | |
| catastrophic cancellation | 7t | alternating taylor series sind(45) | 0.707 | 1 | possible loss of 2 significant figures near origin |
| round off errors, floating point | 3t | sind(45) | 0.7071 | 1 | for small integers, magnitude equivalent to truncation errors |
| floating point representation, transform | 3t | sin(45) | 0.70711 | loss of 1 significant figure, but accumulate | |
| near equal terms, add subtract | 9t | sind(45) | 0.70711 | 1 | possible loss of 3 significant figures |
| polynomial near origin (of computation) | 3t | sind(45) | 0.70711 | 0.001 in 5 places, 3t | possible loss of 3 significant figures or more |
| polynomial approach to zero or poles | 3t | sind(45) | 0.70711 | 0.05 in 5 places, 3t | possible loss of 4 significant figures or more |
| interpolation between terms | 4t | sind(45) | 0.70711 | 1 | possible loss of 2 significant figures or more |
| stable/unstable in accumulated error | 9t | sind(45) | 0.70711 | 1 | unstable in accumulated error may exceed sum of all retained terms, meaningless answer |
Note. Mostly programmer buzz words culled from many books and papers, not all defined or examples in original. Considering single precision here of 7? significant places. Some trig functions may be stable and accurate in regions near origin (small N) , but unstable and inaccurate either far away from origin (large N) or approaching zeros and poles of function.
Screenshots Section
figure 1.
figure 2.
Appendix Code
appendix TCL programs and scripts
Testbed Calculator with fixed testcases and some Pade_trig subroutines
This is a testbed TCL Calculator for Pade_trig functions. Not all Pade_trig procedures here are invoked, but subroutine code can be used in homebrew scripts for comparison. Subroutines like proc pi from AMG, error code for zero/undefined division, proc errorx, and angle reduction procs may invoked or support the alternate subroutines under test below.
# pretty print from autoindent and ased editor
# Sind Functions calculator
# written on Windows XP on TCL
# working under TCL version 8.5.6 and eTCL 1.0.1
# gold on TCL WIKI, 5nov2017
package require Tk
package require math::numtheory
package require math::geometry
package require math::constants
namespace path {::tcl::mathop ::tcl::mathfunc math::numtheory math::geometry math::constants}
set tcl_precision 17
frame .frame -relief flat -bg aquamarine4
pack .frame -side top -fill y -anchor center
set names {{} {degrees :} }
lappend names {answers: radians:}
lappend names {cosd function: }
lappend names {tand function: }
lappend names {cotd function:}
lappend names {secd function: }
lappend names {cscd function: }
lappend names {sind function:}
foreach i {1 2 3 4 5 6 7 8} {
label .frame.label$i -text [lindex $names $i] -anchor e
entry .frame.entry$i -width 35 -textvariable side$i
grid .frame.label$i .frame.entry$i -sticky ew -pady 2 -padx 1 }
proc about {} {
set msg "Calculator for Sind Functions
from TCL WIKI,
written on eTCL "
tk_messageBox -title "About" -message $msg }
proc ::tcl::mathfunc::precision {precision float} {
# tcl:wiki:Floating-point formatting, [AM]
set x [ format "%#.5g" $float ]
return $x
}
#proc errorx always returns a positive error.
#Normally assume $aa is human estimate,
#assume $bb is divinely exact.
# errorx can be used to test pade_trig procs
# loaded on this page.
proc errorx {aa bb} {expr { $aa > $bb ? (($aa*1.)/$bb -1.)*100. : (($bb*1.)/$aa -1.)*100.}}
# start sind procedures
# proc pi from AMG
proc pi {} {expr acos(-1)}
# begin sind procedures
proc sind {aa} {set aa [* $aa $math::constants::degtorad ];return [sin $aa ]}
proc cosd {aa} {set aa [* $aa $math::constants::degtorad ];return [cos $aa ]}
proc tand {aa} {set aa [* $aa $math::constants::degtorad ];return [tan $aa ]}
proc cotd {aa} {set aa [* $aa $math::constants::degtorad ];return [/ 1. [tan $aa ]]}
proc secd {aa} {set aa [* $aa $math::constants::degtorad ];return [/ 1. [cos $aa ]]}
proc cscd {aa} {set aa [* $aa $math::constants::degtorad ];return [/ 1 [sin $aa ]]}
# end sind procedures
proc calculate { } {
global answer2
global side1 side2 side3 side4 side5
global side6 side7 side8
global testcase_number original_angle_side1
incr testcase_number
set side1 [* $side1 1. ]
set side2 [* $side2 1. ]
set side3 [* $side3 1. ]
set side4 [* $side4 1. ]
set side5 [* $side5 1. ]
set side6 [* $side6 1. ]
set side7 [* $side7 1. ]
set side8 [* $side8 1. ]
# testing angle reduction proc
set original_angle_side1 $side1
set side1 [ degree_reduction $side1 ]
set side1x $side1
set side2 [* $side1x $math::constants::degtorad ]
set side3 [ cosd $side1x ]
set side4 [ tand $side1x ]
catch { set side5 [ cotand $side1x ] }
catch { set side6 [ secd $side1x ] }
catch { set side7 [ cscd $side1x ] }
set side8 [ sind $side1x ]
}
proc fillup {aa bb cc dd ee ff gg hh} {
.frame.entry1 insert 0 "$aa"
.frame.entry2 insert 0 "$bb"
.frame.entry3 insert 0 "$cc"
.frame.entry4 insert 0 "$dd"
.frame.entry5 insert 0 "$ee"
.frame.entry6 insert 0 "$ff"
.frame.entry7 insert 0 "$gg"
.frame.entry8 insert 0 "$hh"
}
proc clearx {} {
foreach i {1 2 3 4 5 6 7 8 } {
.frame.entry$i delete 0 end } }
proc reportx {} {
global answer2
global side1 side2 side3 side4 side5
global side6 side7 side8
global testcase_number original_angle_side1
console show;
puts "%|table $testcase_number|printed in| tcl wiki format|% "
puts "&| quantity| value| comment, if any|& "
puts "&| $testcase_number:|testcase_number | |&"
puts "&| $original_angle_side1 :|degrees | original angle reduced for computation |&"
puts "&| $side1 :|degrees | entry angle after reduction |&"
puts "&| $side2 :|answers : conv. radians, used in arc functions | |& "
puts "&| $side3 :|cosd function| |& "
puts "&| $side4 :|tand function| |&"
puts "&| $side5 :|cotd function | |&"
puts "&| $side6 :|secd function | |&"
puts "&| $side7 :|cscd function | |&"
puts "&| $side8 :|sind function | |&"
puts " $math::constants::radtodeg "
puts " $math::constants::degtorad "
# math::geometry::print-geometry
}
frame .buttons -bg aquamarine4
::ttk::button .calculator -text "Solve" -command { set side8 0 ; calculate }
::ttk::button .test2 -text "Testcase1" -command {clearx;fillup 0.0 0.0 1.0 0.0 0.0 1.0 inf 0.0}
::ttk::button .test3 -text "Testcase2" -command {clearx;fillup 180.0 3.14 -1. 0.0 0.0 -1.0 inf 0.0}
::ttk::button .test4 -text "Testcase3" -command {clearx;fillup 360.0 6.28 1.0 0.0 0.0 1.0 -inf 0.0}
::ttk::button .clearallx -text clear -command {clearx }
::ttk::button .about -text about -command {about}
::ttk::button .cons -text report -command { reportx }
::ttk::button .exit -text exit -command {exit}
pack .calculator -in .buttons -side top -padx 10 -pady 5
pack .clearallx .cons .about .exit .test4 .test3 .test2 -side bottom -in .buttons
grid .frame .buttons -sticky ns -pady {0 10}
. configure -background aquamarine4 -highlightcolor brown -relief raised -border 30
wm title . "Sind Functions Calculator"Alternate subroutines under test
proc pi {} {expr acos(-1)} # from AMG
proc radian_reduction {aa} {
set pi [pi]
if { $aa > 0. } {
while {$aa > [* 2. $pi ] } {
set aa [- $aa [* 2. $pi ] ] }
return $aa }
if { $aa < [* -1. 2. $pi ] } {
while {$aa < [* -1. 2. $pi ] } {
set aa [+ $aa [* 2. $pi ] ] }
return $aa }
return $aa } proc trial_degree_reduction_pi {aa} {
if { $aa > 0. } {
while {$aa > 180.} {
set aa [- $aa 180.] } proc degree_reduction {aa} {
if { $aa > 360. } {
while {$aa > 360.} {
set aa [- $aa 360.] }
return $aa }
if { $aa < -360. } {
while {$aa < -360.} {
set aa [+ $aa 360.] }
return $aa }
return $aa }
return $aa }
if { $aa < -180. } {
while {$aa < -180.} {
set aa [+ $aa 180.] }
return $aa }
return $aa } proc trial_degree_reduction_8ths {aa} {
set counter 0
if { $aa > 0. } {
while {$aa > 45.} {
incr counter
set aa [- $aa 45.] }
return $aa }
if { $aa < -45. } {
while {$aa < -45.} {
incr counter
set aa [+ $aa 45.] }
return $aa }
return $aa } # pade_ln (1+x) of 3/3 order used in discussion
proc ln_1_x {x} {
set term2 [ expr { $x + $x**2 + 0.1833333333333333*($x**3)} ] ;
set term3 [ expr { 1 + 1.5*$x + .6*($x**2) + 0.05*($x**3) } ] ;
set result [ expr { $term2 / $term3 } ]
return $result;}
proc sin_neg_flipper_check {aa} {
if {$aa < 0 } {
set keeper [* -1. $aa ]
set keeper2 [ $keeper ]
set keeper2 [* -1. $keeper2 ] }
return $keeper2} proc pi {} {expr acos(-1)}
proc para_sind {aa} {
set aa [* $aa $math::constants::degtorad ];
set pi [pi]
set result [ expr { (16.*($pi-$aa)*$aa) / (5.*$pi*$pi-4.*($pi-$aa)*$aa) }]
}
puts " para_sind 45. [ para_sind 45. ] "
# outout >> para_sind 45. 0.7058823529411673 proc nested_taylor_sind_3ird {x} {
set x [* $x $math::constants::degtorad ];
set result [ expr {(((1./120.)*$x*$x*$x -(1./6.)*$x)*$x +1. )*$x } ]
return $result }
proc nested_taylor_sindx_9th {x} {
set x [* $x $math::constants::degtorad ];
#set result [ expr {(((((1./362880.)*$x*$x -(1./5040))*$x +(1./120.)*$x*$x)*$x -(1./6)*$x)*$x +1. )*$x } ]
set result [ expr { $x*( 1. - $x*$x*( 1./6. - $x*$x*( 1./120. - $x*$x*(1./5040.-$x*$x*(1./362880.)) ))) }]
return $result }
# puts " [ time { set result [ expr { $x*( 1. - $x*$x*( 1./6. - $x*$x*( 1./120. - $x*$x*(1./5040.-$x*$x*(1./362880.)) ))) }] } 1 ] "
# 143 microseconds per iteration
# Taylor sin evaluated at 2 degrees
# nested_sind 2. 0.034899496407940836
# 3th 0.03489949670251291
# 7th 0.034899496407935854
# 9th 0.034899496407940836 diff 9th place
# TCL 8.6 derived sind 0.03489949670250038
# Taylor sin evaluated at 4 degrees
# nested_sind 45. 0.7071067829368578 , diff 8th place
# TCL 8.6 derived sind 0.7071067811865381 proc nested_taylor_cosd_3irdO {x} {
set x [* $x $math::constants::degtorad ];
set result [ expr { (( ( ( (-1./3628800.)*$x*$x+1./40320.)*$x*$x -1./720.)*$x*$x +1./24.)*$x*$x -(1./2.)*$x )*$x +1.} ]
return $result }
# Taylor nested cosd evaluated at 2 degrees
# nested_cosd 2. 0.999392537352738
# TCL 8.5 derived 0.9993908270190958 proc nested_taylor_cosd_10thO {x} {
set x [* $x $math::constants::degtorad ];
set result [expr { 1.−$x*$x*(1./2.-$x*$x*(1./24.−$x*$x*(1./720.−$x*$x*(1./40320.-$x*$x* (1./ 3628800.))))) }]
return $result }
# Taylor cosd evaluated at 2 degrees
# nested_cosd 2. 0.9993908270190958
# TCL 8.5 derived 0.9993908270190958
# numbers seem compatible proc nested_taylor_tand {x} {
set x [* $x $math::constants::degtorad ];
#set result [ expr { $x*(1.+ $x*$x*(1./3.+$x*$x*(17./315.+$x*$x*62./2835.)))}]
set result [ expr { $x*(1.+ $x*$x*(1./3.)+$x*$x*(17./315.+$x*$x*(62./2835.+$x*$x*(4096.*4095.)/(42.*479001600.))))}]
return $result}
# needs checking proc Kurweg_Timmins_Legendre_quotient_tand {aa} {
set aa [* $aa $math::constants::degtorad ];
set term2 [+ [* 34459425. [pow $aa 1 ]] [* -1. 4729725. [pow $aa 3 ]] [* 135135. [pow $aa 5 ]] [* -1. 990. [pow $aa 7 ]] [pow $aa 9 ] ];
set term3 [+ 34459425. [* -1. 16216200. [pow $aa 2 ]] [* 945945. [pow $aa 4 ]] [* -1. 13860. [pow $aa 6 ]] [* 45. [pow $aa 8 ]] ]
set result [/ $term2 $term3 ];
return $result;}
# puts " ...q_tand 45. [ ...q_tand 45. ] "
# timing quotient_tand 45. at 15.59 microseconds per iteration
# Kurweg_Timmins_Legendre_tand 45. = 0.9999999999999736 (9th order)
# ref. Kurweg_Timmins #IEEE paper
proc Kurweg_Timmins_Legendre_quotient_cotand {aa} {
set aa [* $aa $math::constants::degtorad ];
set term2 [+ [* 34459425. [pow $aa 1 ]] [* -1. 4729725. [pow $aa 3 ]] [* 135135. [pow $aa 5 ]] [* -1. 990. [pow $aa 7 ]] [pow $aa 9 ] ];
set term3 [+ 34459425. [* -1. 16216200. [pow $aa 2 ]] [* 945945. [pow $aa 4 ]] [* -1. 13860. [pow $aa 6 ]] [* 45. [pow $aa 8 ]] ]
set result [/ $term3 $term2 ];
return $result;}
# Kurweg_Timmins_Legendre_cotand = (9th order)
# timing on quotient_cotand 90. at 15.52 microseconds per iteration
# quotient_cotand 90. -1.0000000000000264
proc Kurweg_Timmins_Legendre_quotient_sind {aa} {
set aa [* $aa $math::constants::degtorad ];
set term2 [+ [* 34459425. [pow $aa 1 ]] [* -1. 4729725. [pow $aa 3 ]] [* 135135. [pow $aa 5 ]] [* -1. 990. [pow $aa 7 ]] [pow $aa 9 ] ];
set term3 [+ 34459425. [* -1. 16216200. [pow $aa 2 ]] [* 945945. [pow $aa 4 ]] [* -1. 13860. [pow $aa 6 ]] [* 45. [pow $aa 8 ]] ]
set tand [/ $term3 $term2 ];
set quotient_sind [\ $tand [sqrt [ +1. [pow $tand 2 ] ] ]]
set result $quotient_sind
return $result;}
# using Kurweg_Timmins_Legendre_tand (9th order)
proc Kurweg_Timmins_Legendre_quotient_cosd {aa} {
set aa [* $aa $math::constants::degtorad ];
set term2 [+ [* 34459425. [pow $aa 1 ]] [* -1. 4729725. [pow $aa 3 ]] [* 135135. [pow $aa 5 ]] [* -1. 990. [pow $aa 7 ]] [pow $aa 9 ] ];
set term3 [+ 34459425. [* -1. 16216200. [pow $aa 2 ]] [* 945945. [pow $aa 4 ]] [* -1. 13860. [pow $aa 6 ]] [* 45. [pow $aa 8 ]] ]
set tand [/ $term3 $term2 ];
set quotient_cosd [/ 1. [sqrt [ +1. [pow $tand 2 ] ] ]]
set result $quotient_cosd
return $result;}
# using Kurweg_Timmins_Legendre_tand (9th order)
# quotient_cosd 45. 0.7071067811865381
# timing quotient_cosd 45. 17.65 microseconds per iteration
# comparison tcl derived ( w/ math.h) cosd 0.7071067811865569
# tcl derived sind 0.7071067811865381
# tcl derived tand 0.9999999999999735 # Kurweg_Timmins_Legendre combined or catch-all proc
# some formulas maybe commented out
# or output into main deck as global parameters
proc Kurweg_Timmins_Legendre_quotient_cosd {aa} {
set aa [* $aa $math::constants::degtorad ];
set term2 [+ [* 34459425. [pow $aa 1 ]] [* -1. 4729725. [pow $aa 3 ]] [* 135135. [pow $aa 5 ]] [* -1. 990. [pow $aa 7 ]] [pow $aa 9 ] ];
set term3 [+ 34459425. [* -1. 16216200. [pow $aa 2 ]] [* 945945. [pow $aa 4 ]] [* -1. 13860. [pow $aa 6 ]] [* 45. [pow $aa 8 ]] ]
set tand [/ $term3 $term2 ];
#set term4 [+ 1. [pow $tand 2 ] ]
set quotient_cosd [/ 1. [sqrt [+ 1. [pow $tand 2 ] ] ] ]
#set quotient_sind [/ $tand [sqrt [+ 1. [pow $tand 2 ] ] ]]
#set quotient_cscd [/ [sqrt [+ 1. [pow $tand 2 ] ] ] 1.]
#set quotient_secd [/ [sqrt [+ 1. [pow $tand 2 ] ] ] $tand ]
set result $quotient_cosd
return $result;}
puts " quotient_cosd 45. [ Kurweg_Timmins_Legendre_quotient_cosd 45. ] "
puts " timing quotient_cosd 45. [time { Kurweg_Timmins_Legendre_quotient_cosd 45.} 100 ] "
set x [* 45. $math::constants::degtorad ];
puts "comparison tcl derived cosd [ cos $x ] sind [ sin $x ] tand [ tan $x ] "
#quotient_cosd 45. 0.7071067811865381
#timing quotient_cosd 45. 17.57 microseconds per iteration
#comparison figures, tcl derived ( w/ math.h) cosd 0.7071067811865569
# sind 0.7071067811865381
# tand 0.9999999999999735
# quotient_atand 1. 0.7564763336506682
# timing quotient_atand 1. 13.87 microseconds per iteration
# real troubles with below, quotient_atand
proc Kurweg_Timmins_Legendre_quotient_atand {bb} {
set pi $math::constants::pi
set aa [/ 1. $bb ];
set term2 [+ 15159. [* 174455. [pow $aa 2 ]] [* 345345. [pow $aa 4 ]] [* 225225. [pow $aa 6 ]] ];
set term3 [* 35. [+ 35. [* 1260. [pow $aa 2 ]] [* 6930. [pow $aa 4 ]] [* 12012. [pow $aa 6 ]] [* 6435. [pow $aa 8 ]] ]]
set atand [/ $term2 $term3 ];
#set atand [* $atand $math::constants::radtodeg ];}
#if { $bb < 1.2 } { set atand [- [/ $pi 2. ] $atand ] };
set result $atand
return $result;}
puts " quotient_atand 1. [ Kurweg_Timmins_Legendre_quotient_atand 1. ] "
puts " timing quotient_atand 1. [time { Kurweg_Timmins_Legendre_quotient_atand 1.} 100 ] "
# quotient_atand accurate if $bb >> 5
# quotient_atand 1. 0.7564763336506682 (radians here)
# timing quotient_atand 1. 13.87 microseconds per iteration
# Calculations with bb < 1 need transform
# or substitution <pi/2-atan a>. # Maclaurin quotient atand , works but not acc. enough
proc atandt {aa} {
set pi $math::constants::pi
set term2 [expr {$aa+ (7./9.)*$aa**3+(64./945.)*$aa**5 } ];
set term3 [expr {1.+ (10./9.)*$aa**2+(5./21.)*$aa**4 } ];
set atand [/ $term2 $term3 ];
set atand [* $atand $math::constants::radtodeg ];
set result $atand
return $result;}
set quick [/ 20. 11. ]
set quick [/ $math::constants::pi 4 ]
puts " test reboot 1. [ atandt $quick ] "
set quick [/ 20. 11. ]
puts " test reboot 1. [ atandt $quick ] "
set quick [/ 20. 20. ]
puts " test reboot 20. 20. / [ atandt $quick ] "
set x [/ 20. 20. ]
puts "/ 20. 20. comparison tcl derived cosd [cos $x ] sind [sin $x ] tand [tan $x ] atan [atan $x ] "
# test reboot 20. 20. / 45.01073850038125
#/ 20. 20. comparison tcl derived cosd 0.5403023058681398
# sind 0.8414709848078965 tand 1.5574077246549023 atan 0.7853981633974483 proc taylor_cosd {aa} {
set aa [* $aa $math::constants::degtorad ];
set result [ expr { 1.-$aa*$aa/2.+$aa*$aa*$aa*$aa/24.-$aa*$aa*$aa*$aa*$aa*$aa/720. } ]
return $result }
proc cotdx {aa} {set aa [* $aa $math::constants::degtorad ];division_check [cos $aa] [sin $aa ] ; return [/
[cos $aa] [sin $aa ]]}
proc secdx {aa} {set aa [* $aa $math::constants::degtorad ];division_check [1.] [sin $aa ] ;return [/ 1.
[sin $aa ]]}
proc cscdx {aa} {set aa [* $aa $math::constants::degtorad ];division_check [1.] [cos $aa ] ; return [/ 1.
[cos $aa ]]}
proc acotd {aa} {set aa [/ [acos $aa] [asin $aa ]];set aa [* $aa $math::constants::radtodeg ];return $aa}
proc asecd {aa} {set aa [/ 1. [asin $aa ]];set aa [* $aa $math::constants::radtodeg ];return $aa}
proc acscd {aa} {set aa [/ 1. [acos $aa ]];set aa [* $aa $math::constants::radtodeg ];return $aa}
proc sind {aa} {set aa [* $aa $math::constants::degtorad ];return [sin $aa ]}
proc cosd {aa} {set aa [* $aa $math::constants::degtorad ];return [cos $aa ]}
proc tand {aa} {tangent_check $aa ;set aa [* $aa $math::constants::degtorad ];return [tan $aa ]}
proc asind {aa} {set aa [asin $aa ];set aa [* $aa $math::constants::radtodeg ];return $aa}
proc acosd {aa} {set aa [acos $aa ];set aa [* $aa $math::constants::radtodeg ];return $aa}
proc atand {aa} {set aa [atan $aa ];set aa [* $aa $math::constants::radtodeg ];return $aa}
proc sinda {x} {
set x [* $x $math::constants::degtorad ];
set x [ expr { $x* (1. -( $x**2)/6.+ ($x**4)/120.- ($x**6)/5040.+( $x**8)/362880.- ($x**10)/39916800.+ ($x**12)/6227020800.-( $x**14)/1307674368000.) }]
return $x}
# sinda 30. 0.49999999999999234
# start cecil hastings approximation, approaching round off limits
proc atanda {x} {
set pi [* 1. $math::constants::pi ]
set atand [ expr { $pi/4. + .9992150*(($x-1.)/($x+1.)) -.3211819*(($x-1.)/($x+1.))**3 +.1462766*(($x-1.)/($x+1.))**5-.0389929*(($x-1.)/($x+1.))**7 }]
set atand [* $atand $math::constants::radtodeg ];
return $atand}
proc atandgg {x} {
set pi [* 1. $math::constants::pi ]
set atand [ expr { $pi/4. + .99997726*(($x-1.)/($x+1.)) -.33262347*(($x-1.)/($x+1.))**3 +.19354346*(($x-1.)/($x+1.))**5-.11643287*(($x-1.)/($x+1.))**7 +.05265332*(($x-1.)/($x+1.))**9 -.01172120*(($x-1.)/($x+1.))**11 }]
set atand [* $atand $math::constants::radtodeg ];
return $atand}
# atanda 1. 45.000000000013884
# atandgg 1. 45.000000000013884
# end cecil hastings approximation
# begin sind procedures, loaded in testbed above
proc sind {aa} {set aa [* $aa $math::constants::degtorad ];return [sin $aa ]}
proc cosd {aa} {set aa [* $aa $math::constants::degtorad ];return [cos $aa ]}
proc tand {aa} {set aa [* $aa $math::constants::degtorad ];return [tan $aa ]}
proc cotd {aa} {set aa [* $aa $math::constants::degtorad ];return [/ 1. [tan $aa ]]}
proc secd {aa} {set aa [* $aa $math::constants::degtorad ];return [/ 1. [cos $aa ]]}
proc cscd {aa} {set aa [* $aa $math::constants::degtorad ];return [/ 1 [sin $aa ]]}
# end sind procedures
# pretty print from autoindent and ased editor
# small angle transform proc
# written on Windows XP on eTCL
# working under TCL version 8.5.6 and eTCL 1.0.1
# gold on TCL WIKI , 10dec2017
package require Tk
package require math::numtheory
package require math::geometry
package require math::constants
namespace path {::tcl::mathop ::tcl::mathfunc math::numtheory math::geometry math::constants}
set tclprecision 17
console show
wm title . "Console program for small angles and transform"
proc pi {} {expr acos(-1)}
proc pade_sin_testx {aa} {
set aa [* $aa $math::constants::degtorad ];
set term2 [ expr { $aa-31.*$aa*$aa*$aa/294. } ] ;
set term3 [ expr { 1.+3.*$aa*$aa/49.+11.*$aa*$aa*$aa*$aa/5880.} ] ;
set result [ expr { $term2/$term3 } ]}
proc pade_cosd_g {aa} {
set aa [* $aa $math::constants::degtorad ];
set term2 [ expr { 1080.-480.*$aa*$aa+$aa*$aa*$aa*$aa*17. } ] ;
set term3 [ expr { 1080.+60.*$aa*$aa+2.*$aa*$aa*$aa*$aa} ] ;
set result [ expr { $term2/$term3 } ]}
proc taylor_cosd {aa} {
set aa [* $aa $math::constants::degtorad ];
set result [ expr { 1.-$aa*$aa/2.+$aa*$aa*$aa*$aa/24.-$aa*$aa*$aa*$aa*$aa*$aa/720. } ]
return $result }
proc sind {aa} {set aa [* $aa $math::constants::degtorad ];return [sin $aa ]}
proc cosd {aa} {set aa [* $aa $math::constants::degtorad ];return [cos $aa ]}
proc small_angle_sind {aa} { return [/ [* $aa [pi] ] 180. ] }
proc small_angle_cosd {aa} { return [- [/ [pi] 2. ] [/ [* $aa [pi] ] 180. ] ] }
proc small_angle_tand {aa} { return [/ [/ [* $aa [pi] ] 180. ] [- [/ [pi] 2. ] [/ [* $aa [pi] ] 180. ] ] ] }
proc small_angle_cosdx {aa} {return [- 1. [* [* $aa [/ [pi] 180.]] [* $aa [/ [pi] 180.]] .5 ] ] }
# alpha=x*(1./361.);sin(361*alpha)=~~ 2*sin(alpha)*cos (alpha) - sin (alpha)
proc small_angle {aa} {
set alpha [* $aa [/ 1. 361. ]]
set result [- [* 2. [ sind [* 360. $alpha] ] [ cosd $alpha] ] [ sind [* 359. $alpha ]]]
return $result }
puts " small_angle_sind [* 1. [ small_angle 45. ]] taylor_cosd [ taylor_cosd 45.] "
# small_angle_sind 0.7071067811865382
# taylor_cosd 0.7071032148228549 Range aware switch from ranged switch
Test with angle intervals of 90 degrees
# pretty print from autoindent and ased editor
# range switch2 calculator
# written on Windows XP on eTCL
# working under TCL version 8.5.6 and eTCL 1.0.1
# gold on TCL WIKI , 2dec2017
package require Tk
package require math::numtheory
package require math::geometry
package require math::constants
namespace path {::tcl::mathop ::tcl::mathfunc math::numtheory math::geometry math::constants}
set tclprecision 17
console show
wm title . "Range Aware Switch for 360 deg and 4 Quadrants"
proc sind {aa} {set aa [* $aa $math::constants::degtorad ];return [sin $aa ]}
#proc pade_sin_testx {aa} {
proc sindx {aa} {
global angle1
set aa [* $aa $math::constants::degtorad ];
set term2 [ expr { $aa-31.*$aa*$aa*$aa/294. } ] ;
set term3 [ expr { 1.+3.*$aa*$aa/49.+11.*$aa*$aa*$aa*$aa/5880.} ] ;
set result [ expr { $term2/$term3 } ]}
proc pade_cosd_g {aa} {
set aa [* $aa $math::constants::degtorad ];
set term2 [ expr { 1080.-480.*$aa*$aa+$aa*$aa*$aa*$aa*17. } ] ;
set term3 [ expr { 1080.+60.*$aa*$aa+2.*$aa*$aa*$aa*$aa} ] ;
set result [ expr { $term2/$term3 } ]}
#switch2 from Lars H:
proc exprSwitch2 {switches} {
set cmd ""
foreach {expr body} $switches {lappend cmd elseif $expr then $body}
uplevel 1 [lreplace $cmd 0 0 ::if]
}
proc demo {} {
global angle1
set result 1.
set aa 0
while {$aa < 360.} {
set comment ""
set angle1 $aa
exprSwitch2 {
{$angle1< 0} {set comment "less than 0 deg [ sindx $angle1 ] compare TCL_f [
sind $angle1 ] "; set result [ sind $angle1 ]] }
{$angle1<90 && $angle1>0} {set comment "positive between 0 and 90 deg ,[ sindx $angle1 ] compare
TCL_f [ sind $angle1 ]"; set result [ sind $angle1 ] }
{$angle1 <180 && $angle1>90} {set comment "between 90 and 180 deg, [ sindx [- 180. $angle1 ] ]
compare TCL_f [ sind $angle1 ]"; set result [ sind $angle1 ] }
{$angle1 <270 && $angle1>90} {set comment "between 180 and 270 deg,[* -1. [ sindx [- $angle1
180.] ] ] compare TCL_f [ sind $angle1 ]"; set result [ sind $angle1] }
{$angle1 <360 && $angle1>270} {set comment "between 270 and 360 deg, [* -1. [ sindx [- $angle1
270. -90.] ] ] compare TCL_f [ sind $angle1 ]"; set result [ sind $angle1] }
{$angle1>360} {set comment "greater than 360 deg, [ sindx $angle1 ] compare
TCL_f [ sind $angle1 ] "; set result [ sind $angle1] }
}
incr aa 5
puts "$angle1 is $comment"}
return $result}
puts " [ demo ] "
puts "[ sindx 45 ]"
puts "[ sindx 45. ]"sample output
5 is positive between 0 and 90 deg@,0.08715574274765489 compare TCL_f 0.08715574274765671
10 is positive between 0 and 90 deg@,0.17364817766599888 compare TCL_f 0.17364817766692744
35 is positive between 0 and 90 deg@,0.5735763655797433 compare TCL_f 0.5735764363510376
40 is positive between 0 and 90 deg@,0.6427873769178369 compare TCL_f 0.6427876096865303
45 is positive between 0 and 90 deg@,0.7071061177657524 compare TCL_f 0.7071067811865381
50 is positive between 0 and 90 deg@,0.766042754816006 compare TCL_f 0.7660444431189686
150 is between 90 and 180 deg, 0.4815886300755488 compare TCL_f 0.5000000000000384
# loses useful accuracy beyond pi/2 here, so "fold " sin calculations onto 1st interval ( 0... pi/2)
340 is between 270 and 360 deg, -2.940152165863797 compare TCL_f -0.3420201433257629
345 is between 270 and 360 deg, -2.9931926693661937 compare TCL_f -0.2588190451026194
350 is between 270 and 360 deg, -3.0438074377978768 compare TCL_f -0.17364817766703186
# alternative is to " fold " sin calculations onto some sin and cos functions onto 1st interval ( 0... pi/2)
# some alternative homebrews use the cos function included on the console program script
# still getting unacceptable errors beyond 45 deg or pi/4
340 is between 270 and 360 deg, -0.3119297601688663 compare TCL_f -0.3420201433257629
345 is between 270 and 360 deg, -0.22093842832380617 compare TCL_f -0.2588190451026194
350 is between 270 and 360 deg, -0.12641192920432537 compare TCL_f -0.17364817766703186
355 is between 270 and 360 deg, -0.028781653705219044 compare TCL_f -0.08715574274776272
# here, second pi/4 (45 deg) interval folded into pade_cos onto 1st interval ( 0... pi/2)
# agreement with TCL derived sin f to about 6 places (with pi/4 folding & (3/4) order Pade f.)
45 is positive between 0 and 90 deg ,0.7071034367666852 compare TCL_f 0.7071067811865381
50 is positive between 0 and 90 deg ,0.7660431199952724 compare TCL_f 0.7660444431189686
80 is positive between 0 and 90 deg ,0.9848077529909282 compare TCL_f 0.9848077530122039
85 is positive between 0 and 90 deg ,0.9961946980916621 compare TCL_f 0.9961946980917433"Umut Tech fast sine algorithm" into TCL on the TCL/wiki
Test with angle intervals of 10 degrees
# pretty print from autoindent and ased editor
# Umut Tech fast sine algorithm" into TCL
# written on Windows XP on eTCL
# working under TCL version 8.5.6 and eTCL 1.0.1
# gold on TCL WIKI , 20dec2017
package require Tk
package require math::numtheory
package require math::geometry
package require math::constants
package require math::bigfloat
namespace path {::tcl::mathop ::tcl::mathfunc math::numtheory math::geometry math::constants math::bigfloat}
#namespace import ::math::bigfloat::*
#set tclprecision 17
global place_holder_ten small_angle lindexer
console show
proc sind {aa} {set aa [* $aa $math::constants::degtorad ];return [sin $aa ]}
proc sindx {aa} {
global angle1
set aa [* $aa $math::constants::degtorad ];
set term2 [- $aa [/ [* 31. $aa $aa $aa ] 294.] ];
set term3 [+ 1. [/ [* 3. $aa $aa] 49. ] [/ [* 11. $aa $aa $aa $aa] 5880.] ] ;
set result [ expr { $term2/$term3 } ]}
proc pade_cosd_g {aa} {
set aa [* $aa $math::constants::degtorad ];
set term2 [+ 1080. [* -1. 480. $aa $aa ] [* $aa $aa $aa $aa 17.] ] ;
set term3 [+ 1080. [* 60. $aa $aa ] [* 2. $aa $aa $aa $aa] ]
set result [ expr { $term2/$term3 } ]}
proc degree_reduction {aa} {
if { $aa > 360. } {
while {$aa > 360.} {
set aa [- $aa 360.] }
return $aa }
if { $aa < -360. } {
while {$aa < -360.} {
set aa [+ $aa 360.] }
return $aa }
return $aa }
proc degree_lindex_selection {aa} {
global place_holder_ten small_angle lindexer
set aa [abs $aa ]
if { $aa < 100. } {
set lindexer -1
foreach x {0 10 20 30 40 50 60 70 80 90} {
set place_holder_ten $x
set small_angle [- $aa $place_holder_ten ]
incr lindexer
#puts "$lindexer $x place_holder_ten $place_holder_ten $small_angle"
if { $small_angle < 10 } {
break
}
}
return $aa }
return $aa }
proc umut_fast_sind {aa} {
global place_holder_ten small_angle lindexer
set fast_sine $aa
set testcase_number 1
set sine_table {1. 2. 3. 4. 5.}
set cos_table {1. 2. 3. 4. 5.}
set sine_table {
0.0
0.17364817766693034885171662676931
0.34202014332566873304409961468226
0.5
0.64278760968653932632264340990726
0.76604444311897803520239265055542
0.86602540378443864676372317075294
0.93969262078590838405410927732473
0.98480775301220805936674302458952
1.0
}
set cos_table_original {
1.0
0.99984769515639123915701155881391
0.99939082701909573000624344004393
0.99862953475457387378449205843944
0.99756405025982424761316268064426
0.99619469809174553229501040247389
0.99452189536827333692269194498057
0.99254615164132203498006158933058
0.99026806874157031508377486734485
0.98768834059513772619004024769344 }
set cos_table {
1.0
0.98480775301220805936674302458952
0.93969262078590838405410927732473
0.86602540378443864676372317075294
0.76604444311897803520239265055542
0.64278760968653932632264340990726
0.5
0.34202014332566873304409961468226
0.17364817766693034885171662676931
0.0 }
set aa [degree_reduction $aa ]
set aa [degree_lindex_selection $aa ]
set fast_sine $aa
set fast_sine [+ [* [ lindex $sine_table $lindexer ] [ pade_cosd_g $small_angle]] [* [ sindx $small_angle ] [lindex $cos_table $lindexer ]]]
return $fast_sine }
puts " umut_fast_sind [ umut_fast_sind 15.004 ] tcl sine derived [ sind 15.004 ]"
puts " umut_fast_sind timing [ time {umut_fast_sind 95.004} 1000 ] tcl sine derived [time { sind 95.004 } 1000]" #taylor tangent series,
set tan_taylor [ expr { $x + (1./3.) *$x**3 + (2./15.) *$x**5 + (17./315.) *$x**7 + (62./2835.) *$x**9 + (1382./155925.) *$x**11 + (21844./6081075.) *$x**13 + (929569./638512875.) *$x**15 + (6404582./10854718875.) *$x**17 + (443861162./1856156927625.) *$x**19 } ] # large pade expressions, written for 0< x < pi/4
# intended for conventional single precision, error < 1E-9
proc tanx_tester {x} {
set x [* $x $math::constants::degtorad ]
set tanx_tester [ expr { (-55.*$x**9 + 25740.*$x**7 - 2837835.*$x**5 + 91891800.*$x**3 - 654729075.*$x)/($x**10 - 1485.*$x**8 + 315315.*$x**6 - 18918900.*$x**4 + 310134825.*$x**2 - 654729075.) } ]
return $tanx_tester}
proc cosx_tester {x} {
set x [* $x $math::constants::degtorad ]
set cosx_tester [ expr { (80737373./147173.*$x**8 - 13853547000./147173.*$x**6 + 727718024880./147173.*$x**4 - 867308904000./11321.*$x**2 + 1814976979200./11321.)/($x**8 + 39328920./147173.*$x**6 + 5772800880./147173.*$x**4 + 40179585600./11321.*$x**2 + 1814976979200./11321.) } ]
return $cosx_tester}
proc sinx_tester {x} {
set x [* $x $math::constants::degtorad ]
set sinx_tester [ expr { (4585922449./46306665.*$x**9 - 23689420744./1029037.*$x**7 + 1850756539632./1029037.*$x**5 - 51192938596800./1029037.*$x**3 + 346781323848960./1029037.*$x)/($x**8 + 345207016./1029037.*$x**6 + 61570292784./1029037.*$x**4 + 6603948711360./1029037.*$x**2 + 346781323848960./1029037.) } ]
return $sinx_tester}
proc atand_tester {x} {
#set x [* $x $math::constants::degtorad ]
set atand_tester [ expr { (16384./99225.*$x**9 + 14179./2205.*$x**7 + 11869./315.*$x**5 + 1859./27.*$x**3 + 2431./63.*$x)/($x**8 + 44./3.*$x**6 + 286./5.*$x**4 + 572./7.*$x**2 + 2431/63.) } ]
set atand_tester [* $atand_tester $math::constants::radtodeg ]
return $atand_tester}
proc tandax {x} {
set x [* $x $math::constants::degtorad ]
set term2 [ expr { (1./120.)*$x**15 - (119./2.)*$x**13 + (264537./4.)*$x**11 - (101846745./4.)*$x**9 + (33129291195./8.)*$x**7 - (1159525191825./4.)*$x**5 + (61665657928875./8.)*$x**3 - (412685556908625./8.)*$x }]
set term3 [ expr { $x**14 - (4641./2.)*$x**12 + (2909907./2.)*$x**10 - (1440403965./4.)*$x**8 + (77301679455./2.)*$x**6 - (6851739769875./4.)*$x**4 + (99613755115875./4.)*$x**2 - (412685556908625./8.)} ]
set tandax [ expr { $term2/$term3 } ]
return $tandax}
proc cotandax {x} {
set x [* $x $math::constants::degtorad ]
set term2 [ expr { (1./120.)*$x**15 - (119./2.)*$x**13 + (264537./4.)*$x**11 - (101846745./4.)*$x**9 + (33129291195./8.)*$x**7 - (1159525191825./4.)*$x**5 + (61665657928875./8.)*$x**3 - (412685556908625./8.)*$x }]
set term3 [ expr { $x**14 - (4641./2.)*$x**12 + (2909907./2.)*$x**10 - (1440403965./4.)*$x**8 + (77301679455./2.)*$x**6 - (6851739769875./4.)*$x**4 + (99613755115875./4.)*$x**2 - (412685556908625./8.)} ]
set cotandax [ expr { $term3/$term2 } ]
return $cotandax}
proc cscdxx {x} {
set x [* $x $math::constants::degtorad ]
set term2 [ expr { (4585922449./46306665.)*$x**9 - (23689420744./1029037.)*$x**7 + (1850756539632./1029037.)*$x**5 - (51192938596800./1029037.)*$x**3 + (346781323848960./1029037.)*$x}]
set term3 [ expr { ($x**8 + (345207016./1029037.)*$x**6 + (61570292784./1029037.)*$x**4 + (6603948711360./1029037.)*$x**2 + (346781323848960./1029037.) } ]
set cscdxx [ expr { $term3/$term2 } ]
return $cscdxx}
proc secdxx {x} {
set x [* $x $math::constants::degtorad ]
set term2 [ expr { (80737373./147173.)*$x**8 - (13853547000./147173.)*$x**6 +(727718024880./147173.)*$x**4 - (867308904000./11321.)*$x**2 + (1814976979200./11321.) } ]
set term3 [ expr { $x**8 + (39328920./147173.)*$x**6 + (5772800880./147173.)*$x**4 + (40179585600./11321.)*$x**2 + (1814976979200./11321.) } ]
set secdxx [ expr { $term3/$term2 } ]
return $secdxx}
proc asind_tester {x} {
#set x [* $x $math::constants::degtorad ]
set asind_tester [ expr { ((17487984593./45057791975.)*$x**7 - (51478547544./6436827425.)*$x**5 +
(6582023536./257473097.)*$x**3 - (25784176704./1287365485.)*$x)/($x**6 - (59441400./5254553.)*$x**4 +
(759336336./26272765.)*$x**2 - (25784176704./1287365485.)) } ]
set asind_tester [* $asind_tester $math::constants::radtodeg ]
return $asind_tester} tanx_tester 45. 0.9999999999999736 & 0.9999999999999735 errorx 2.220446049250313e-14
tanx_tester 45. 0.9999999999999736 & 0.9999999999999735 errorx 2.220446049250313e-14
cosx_tester 45. 0.7071067811865569 & 0.7071067811865569 errorx 0.0
sinx_tester 45. 0.7071067811865381 & 0.7071067811865381 errorx 0.0
atanx_tester 1. 0.7853983279699818 & 0.7853981633974483 errorx 2.0954025758967987e-5
atand_tester 1. 45.00000942932548 errorx 2.0954025758967987e-5
sin_tester 20. 0.34202014355557075 & 0.34202014332566316 errorx 6.722047363183492e-8
sin_tester 10. 0.17364817802842505 & 0.17364817766692744 errorx 2.08178185800989e-7
cscdxx tester 45. 0.7071067811865381
secdxx 45. 1.4142135623730763
#asind_tester .5 29.999999807612248 # tangent pade 15/15 in horner form, time savings???
proc tandaxxx {x} {
set x [* $x $math::constants::degtorad ]
set term2 [ expr { 1/120.*((((((($x**2 - 7140.)*$x**2 + 7936110.)*$x**2 - 3055402350.)*$x**2 + 496939367925.)*$x**2 - 34785755754750.)*$x**2 + 924984868933125.)*$x**2 - 6190283353629375.)*$x }]
set term3 [ expr { 1/4.*((((2*((2*$x**2 - 4641.)*$x**2 + 2909907.)*$x**2 - 1440403965.)*$x**2 + 154603358910.)*$x**2 - 6851739769875.)*$x**2 + 99613755115875.)*$x**2 - 412685556908625./8. } ]
set tandax [ expr { $term2/$term3 } ]
return $tandax}
#45 deg comparison tcl derived tandaxxx
tandaxxx 0.9999999999999732 errorx 2.220446049250313e-14 percent
cosd 0.7071067811865569
sind 0.7071067811865381
tand 0.9999999999999735, derived from standard math library
#45 deg comparison time tandaxxx ( horner) 15.34 microseconds per iteration
vs non-horner 18.8 microseconds per iteration
tcl tan time est 1.4 microseconds per iteration
# cotangent pade 15/15 in horner form, time savings???
proc cotandaxxx {x} {
set x [* $x $math::constants::degtorad ]
set term2 [ expr { 1/120.*((((((($x**2 - 7140.)*$x**2 + 7936110.)*$x**2 - 3055402350.)*$x**2 + 496939367925.)*$x**2 - 34785755754750.)*$x**2 + 924984868933125.)*$x**2 - 6190283353629375.)*$x }]
set term3 [ expr { 1/4.*((((2*((2*$x**2 - 4641.)*$x**2 + 2909907.)*$x**2 - 1440403965.)*$x**2 + 154603358910.)*$x**2 - 6851739769875.)*$x**2 + 99613755115875.)*$x**2 - 412685556908625./8. } ]
set cotandax [ expr { $term3/$term2 } ]
return $cotandax}
# 45 deg comparison
# cotandaxxx 45 1.0000000000000266
# cotan 1.0000000000000266 , from formula cos/sin, not in standard library
# speedy? conversion formulas for tangent to other trig functions
set t [.5 $t ]
set t [tan $t ]
set sin [/ [* 2. $t ] [+ 1. [** $t 2 ]] ]
set csc? [/ [+ 1. [** $t 2 ]] [* 2. $t ] ]
set cos [/ [- 1. [** $t 2 ]] [+ 1. [** $t 2 ]] ]
set sec? [/ [+ 1. [** $t 2 ]] [- 1. [** $t 2 ]] ]
set cosx [+ [ sin $x ] [/ $pi 2. ] ]
set acosx [ expr { atan((sqrt(1-$x**2))/$x) } ] # valid professional
set asinx_x? [ expr { atan($x/(sqrt(1-$x**2))) } ] # valid???
set atan_x [ expr { asin ($x/(sqrt(1+$x**2))) } ] # valid, CRC tables
cos A = x/1 = x
sin A = sqrt (1-x**2)
tan A = (sqrt(1-x^2))/x
d arctan 1/(1+x**2) # professional
d arcsin 1/sqrt(1-x**2) # professional
d arccos -1/sqrt(1-x**2) # professional
d arcsec +1/(|$x|*(sqrt(x**2-1))) # professional
d arccsc -1/(|$x|*(sqrt(x**2-1))) # professional
d arccot -1/(1+x**2) # professional
proc acosxxx {x} {set acos [ expr { atan((sqrt(1-$x**2))/$x) } ]; return [* $acos $math::constants::radtodeg ]}
#acosxxx .5 60.00000000001851
proc asinx {x} {set asinx [ expr { atan($x/(sqrt(1-$x**2))) } ]; return [* $asinx $math::constants::radtodeg ]}
#asinx .5 30.000000000009262
proc atandx2 {x} {set atandx [ expr { asin ($x/(sqrt(1+$x**2))) } ]; return [* $atandx $math::constants::radtodeg ]}
# atandx2 (r) .5 0.4636476090008061 tcl_tan 0.4636476090008061
proc acotdx {x} {set acotdx [ expr { acos ($x/(sqrt(1+$x**2))) } ]; return [* $acotdx $math::constants::radtodeg ]}
proc acscdx {x} {set acotdx [ expr { atan (1./(sqrt($x**2-1.))) } ]; return [* $acotdx $math::constants::radtodeg ]} # condition that x >= 0
# generate Pade expressions
# Sagemath script, 30Dec2017 on TCL WIKI
# written on Windows XP
# working under TCL version 8.6
# gold on TCL WIKI, 30Dec2017
t = var('t')
f = tan(t)
f.taylor(t,0,42)
s_poly = f.taylor(t,0,42)
f.taylor(t,0,42).power_series(QQ).pade(9,9)
# end # generate horner expressions
t = var('t')
f = tan(t)
f.taylor(t,0,5)
s_poly = f.taylor(t,0,5)
s_poly.horner(t)
#1/15*((2*t^2 + 5)*t^2 + 15)*t
# end # generate pade expressions into horner forms for computation
# should save some computation time
# Sagemath script, 30Dec2017 on TCL WIKI
# written on Windows XP
# working under TCL version 8.6
# gold on TCL WIKI, 30Dec2017
t = var('t')
f = tan(t)
f.taylor(t,0,42)
s_poly = f.taylor(t,0,42)
f.taylor(t,0,42).power_series(QQ).pade(9,9)
# num/denum= (1/45*t^9 - 22*t^7 + 3003*t^5 - 105105*t^3 + 765765*t)/(t^8 - 308*t^6 + 21021*t^4 -
360360*t^2 + 765765)
# upper term
s_poly =(1/45*t^9 - 22*t^7 + 3003*t^5 - 105105*t^3 + 765765*t)
s_poly.horner(t)
#end
# lower term
s_poly =(t^8 - 308*t^6 + 21021*t^4 - 360360*t^2 + 765765)
s_poly.horner(t)
# end
# num=1/45*((((t^2 - 990)*t^2 + 135135)*t^2 - 4729725)*t^2 + 34459425)*t
# denum=(((t^2 - 308)*t^2 + 21021)*t^2 - 360360)*t^2 + 765765
# puts pade tangent into horners formComments Section
gold 3JAN2018, comment received from internet,2018-01-05,sic below.
I have received small code snippet from math.berkeley.edu, which is flexible enough to handle most cases in question. Apparently, the cut and paste horner (text fixed) expressions are not being used-reported much (in monographs), whereas the iterative code and symbolic computation is more flexible. Added SageMath code to output pade and horner expressions of Taylor Polynomials. Apparently, not much hard copy (cut and paste) published on horner forms lately. thanks,gold
from math.berkeley.edu. The coefficients of the nested forms are the same as the plain power series, so you can look them up in any calculus book. For example, sin(x) = x - x^3/3! + x^5/5! - x^7/7! + ... So you would precompute a1=1, a3=-1.0/3!, a5=1.0/5!, a7=1.0/7!, etc. Using periodicity of sin(x) as well as double-angle formulas, you can assume |x|<=1. So if you want 16 digits of accuracy, you should compute out to a_19 = -1/19! = 1.2164510040883200*10^17 .Then to evaluate sin(x), you would use Horner's rule like this: ---
val = a_19 for (j=18; j>=0; j--) val = ret*x + a_j or better yet val = a_19 for (j=17; j>=1; j-=2) val = ret*x*x + a_j val *= x;
whoops, I copy-pasted 19! instead of -1/19!. You could actually stop at 1/17!=2.8114572543455208e-15 since the first omitted term (x^19/19!) is an error bound in the alternating series case.
arjen - 2018-01-09 08:55:25
I would rely as much as possible on the hardware and very low-level software to evaluate these functions. That is: use simple techniques to reduce the argument and then invoke the ordinary sin, cos, tan etc functions to do the hard work. For instance: sind(98.0) -> cos(8.0/180.0*pi) by first recognising that the argument is 90.0+8.0 degrees, apply the sum formula for the sine function, recognise that sind(90.0) would be exactly 1 and cosd(90.0) is exactly 0. Then the error you make is minimal. Or even simpler: if the argument is not an exact multiple of 90.0, then simply convert to radians. (Note: there is no standard for evaluating the trigonometric functions but library developers do their best to be as accurate as possible as fast as possible).
gold Thanks for feedback. This page is a learning experience (for me). These pade_trig functions in script are very slow and inaccurate past pi/4, compared to the hardware solutions. From the literature, there are cases where the hardware solutions were not checked or reported correctly (ref fsin and FDIV above). The original testbed used the ordinary TCl sin, cos, tan etc functions rather than the Pade functions. Ref your advice, I can reinstall the ordinary TCL sin, cos, and tan functions in the testbed. I will leave the pade_trig procs and Sagemath script (Taylor/Pade/Horner generators) in the alternate listings for the curious reader. If saving computation time, the Sagemath script should be able to convert the odd polynomial into Horner form. I don't see many procs of Pade quotient functions in TCL language on this wiki, so maybe something has been gained.
gold 28Dec2018. All, See better routines and current methods for angle reduction, sin, cos, etc in the TCL core distribution and TCLLIB,as of Jul2018.
Please place any comments here with your wiki MONIKER and date. Thanks,gold,12DEC2018.
| Category Numerical Analysis | Category Toys | Category Calculator | Category Mathematics | Toys and Games | Category Games | Category Application | Category GUI |