Seaching for Babylonian Triplets Slot Calculator Example
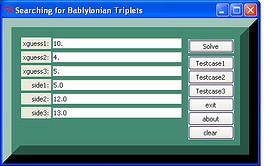
Searching for Babylonian Triplets Slot Calculator Example
This page is under development. Comments are welcome, but please load any comments in the comments section at the bottom of the page. Please include your wiki MONIKER and date in your comment with the same courtesy that I will give you. Aside from your courtesy, your wiki MONIKER and date as a signature and minimal good faith of any internet post are the rules of this TCL-WIKI. Its very hard to reply reasonably without some background of the correspondent on his WIKI bio page. Thanks, gold 6/12/2021 updated.
- Introduction
- Prime Numbers on Clay Tablets
- pseudocode on the triplet algorithm
- Reconstructed listing of the triplets on Tablet Plimpton 322
- Conjectures on possible uses of triplets.
- pseudocode on Babylonian triplets
- pseudocode on development of Babylonian triplets
- Other tablets supporting the use of Plimpton 322 triplets.
- Alternate provisional text, update under construction
- Relations of Heron’s law
- Conclusions
- *
- *
- "Wedge" (triangle) coefficients for cuneiform math from clay tablets
- More inverse pairs of reciprocals
- pseudocode on finding more inverse pairs of reciprocals
- Triplets & Inscribed Circles
- Conclusions
- Screenshots Section
- 6/22/2021, update under construction
- figure 7. Babylonian_Triplets_ full tablet extension
- figure 8. Babylonian_Triplets_percentage_error
- figure 9. Babylonian_Triplets_heron_formula
- figure 10. Babylonian_Triplets Adjacent sides normalized to opposite sides
- figure 11. Babylonian_Triplets Diagonals sides normalized to opposite sides
- figure 12. Possible interpretations of Babylonian_Triplets_angles
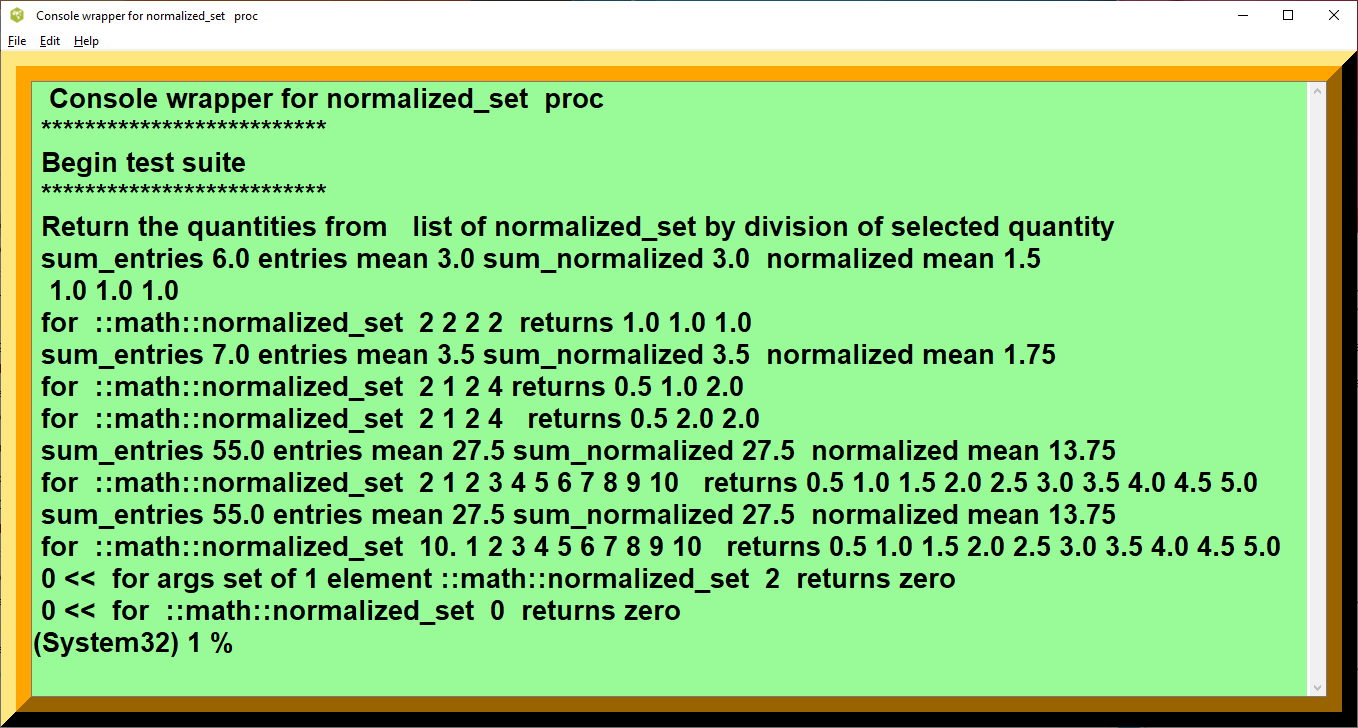
- figure 13. Console helper for normalized_set of Babylonian_Triplets
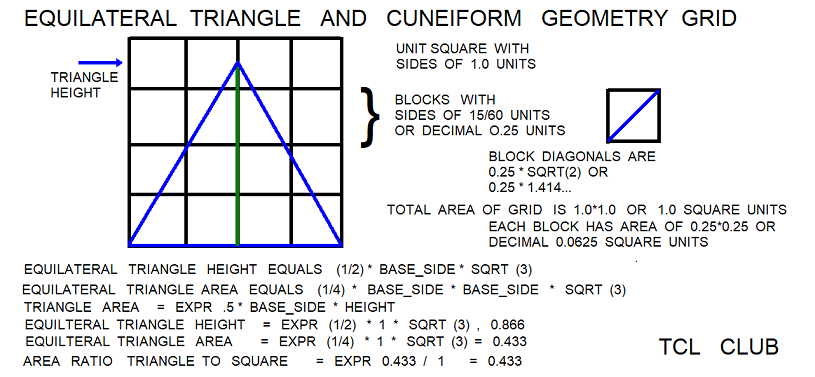
- figure 14. Searching for Babylonian Triplets equilateral triangle
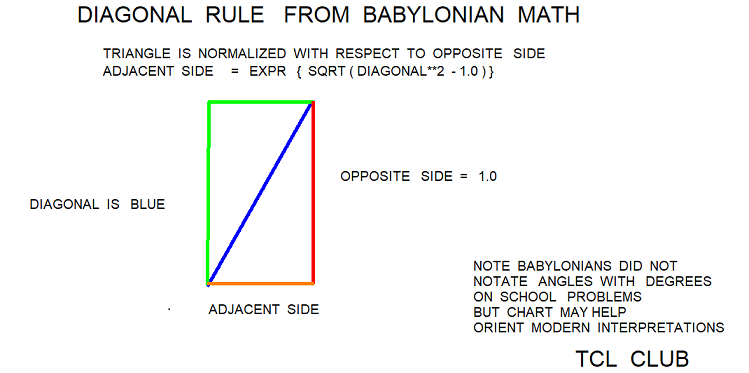
- figure 15 . Searching for Babylonian Triplets diagonal rule
- References:
- Subroutine Math Template 4, Console Wrapper for list of normalized_set
- Test Suite printout for list of normalized_set
- Changes Log Section
- Hidden Comments Section
Introduction
gold Here is an eTCL script on searching for Babylonian triplets or triples. I have modified a slot calculator in eTCL to handle the search procedure for generating triplets. For now, the calculator works with a generating integer. Tap in N, eg. 1,2,3,...N and the sequence of a Babylonian triplet should be returned.
A clay tablet was discovered in Babylon giving examples of triplet numbers which were the sides of a triangle. eg. 3:4:5, While these clay findings predate Pythagoras, this page will use the accepted modern terminology and punctuation, where possible. Triplets include 3:4:5 and 8:15:17. One of the larger written triplets on the clay tablet was 3367:3456:4825. One paper indicated the order of the Babylonian terms was x?/c**2,a,c,d where c would be the hypotenuse, a the shortest side of a right triangle, and d is the line number (1-15). Given that a**2+b**2=c**2 >> b**2=c**2-a**2 >> b**2= (1-a**2)/c**2 for the right triangle, the first term may represent a solution step for b**2, either in the form of b**2/c**2 or (1-a**2)/c**2.
Many of the Babylonian math problems on triangles. rectangles, and modern derivations rely on normalized triplets and multiple number sets with one or two sides normalized to 1. A console wrapper program was written to normalize sets of triplets.
Prime Numbers on Clay Tablets
gold Update, 6/6/2021. In some sense, the Plimpton 322 clay tablet is also generating a set of prime numbers in the available triplet collection on the clay tablet. The Babylonian regular numbers in base_60 between 0 and 60 have a limited set of triplets that satisfy 1< X-1/X < 1+sqrt(2) which appears to be the role of Plimpton 322. The limit 1< X-1/X < 1+sqrt(2) may explain the 1<X<2 limit on the Late Babylonian many place reciprocal tablets.
From the Plimpton 322 tablet, Fernando Quinonez reported that the prime numbers of the set d (column d) are coincedent with Gauss formula < 4n + 1> and that prime numbers of set a (column a) are mixed forms, including the Gauss formula <4n + 1> and another formula < 4n + 3>. On the Plimpton 322 tablet, 8 of 15 readable numbers were prime numbers. The percentage of prime numbers was expr { (8./15.) * 100.}, 53.3 percent rounded.
While the modern mathematicians are trying to find prime numbers in base_10, the Babylonian mathematicians in base_60 were trying to avoid prime numbers. The primes are the Achilles heel of the Babylonian multiplication system using reciprocals in base_60. The number set in the sequence {7 11 13 14} was especially foul to the Babylonian multiplication system, although the Babylonian mathematicians did use the set {7 11 13 14} in arithmetic or "advanced non-standard" calculations. One trick that the Babylonian mathematicians was to multiply an odd number or prime number by 2 or 3 at one early stage of the calculations and then divide out respectfully the 2 or 3 at a later stage of the calculations. For example, 7*2 converts an overtly prime number to a number 14 with factors 2*7. However, this multiplication trick with 2 or 3 as factors is confusing in the extant school and library tablets, so sometimes the modern reader is stressed by a missing factor of 2/3 after corrupted or dropped tablet lines.
| table 1 Percentage Primes in Modern Base_10 and Babylonian Base_60 | printed in | tcl wiki format | |
|---|---|---|---|
| quantity | value | value | comment, if any |
| set_number: | percent of prime numbers in set | percent primes in set of 10 over / set of N | |
| set 10 : | 44.44 | 1.0 | Modern base_10 |
| set 20 : | 42.10 | 1.05 | Archaic IndoEuropean base_20 |
| set 30 : | 34.48 | 1.28 | |
| set 40 : | 30.76 | 1.44 | |
| set 50 : | 30.61 | 1.45 | |
| set 60 : | 28.81 | 1.54 | Babylonian base_60 |
| set 70 : | 27.53 | 1.61 | |
| set 80 : | 27.84 | 1.59 | |
| set 90 : | 26.96 | 1.64 | |
| set 100 : | 25.25 | 1.76 | |
| set 110 : | 26.60 | 1.67 | |
| set 120 : | 25.21 | 1.76 |
;# using TCLLIB math prime subroutines
;# COUNTING SETS OF 10 WITH PERCENTAGE OF PRIMES RELATIVE TO BASE_10
puts "%| set_number:|percent of prime numbers in set | |%"
foreach value {10 20 30 40 50 60 70 80 90 100 110 120} {
puts "&| set $value :|[ expr { [llength [ primesLowerThan [- $value 1 ] ]]*100./ [- $value 1 ] }] |[ expr { ([llength [ primesLowerThan [- 10 1 ] ]]*100./ [- 10 1 ] )/( [llength [ primesLowerThan [- $value 1 ] ]]*100./ [- $value 1 ]) }] | |&" }The calculator and buttons presented here are largely based on the Slot Calculator Demo. See https://wiki.tcl-lang.org/22245 The triplet algorithm was posted by Robert Simms, 11 June 1997, http://www.math.clemson.edu/~rsimms . The console script for triplets at the bottom of page shows what TCL can do in a few simple lines. The best thesis on the triplets was by E.C. Zeeman, referenced below. Another source of triplet info was Dr. Math of Mathforum, listed in refs.
In terms of pseudocode, should find the nearest even numbered power of 2 under N. Add 2**N + 1? for side. then find an odd power of three to add portion for side 3. Since powers of 2 and 3 can hog computer time, will limit searches to small N. (with limit statements in calculator.)
pseudocode on the triplet algorithm
pseudocode: count integers to N
pseudocode: count powers of 2 along the way
and estimate if conditions prevail.
pseudocode: find the highest and nearest
even numbered power of 2 under N.
pseudocode: then find an odd power of three
Pseudocode: add quantity to raise side.
Pseudocode: take sqrt(c**2-a**2) to find remaining side
pseudocode: to zero
pseudocode: load results into 3 answer fields,
pseudocode: & zeros displayReconstructed listing of the triplets on Tablet Plimpton 322
Triplet a,b,c & angle in degrees
| Table of triplets | printed in TCL format | |||
|---|---|---|---|---|
| Triplets as triangle sides a,b,c & angle in degrees | ||||
| a = adjacent side | b = opposite side | c = hypotenuse | angle in degrees | comments, if any |
| 119 | 120 | 169 | 44.8 | |
| 3367 | 3456 | 4825 | 44.3 | |
| 4601 | 4800 | 6649 | 43.8 | |
| 12709 | 13500 | 18548 | 43.3 | largest triangle extant on clay tablet |
| 65 | 72 | 97 | 42.1 | |
| 319 | 360 | 481 | 41.5 | |
| 2291 | 2700 | 3541 | 40.3 | |
| 799 | 960 | 1249 | 39.8 | |
| 481 | 600 | 769 | 38.7 | |
| 4961 | 6480 | 8161 | 37.4 | |
| 3 | 4 | 5 | 37.4 | common triangle in math problems, especially with larger triangles of similarity |
| 1679 | 2400 | 2929 | 35 | |
| 161 | 240 | 289 | 33.9 | |
| 1771 | 2700 | 3229 | 33.3 | |
| 28 | 45 | 53 | 31.9 | |
| 175 | 288 | 337 | 31.3 | |
| Notes | using modern terms, alphabet and "Greek" sides for right triangle | |||
| Babylonians did use angles and degrees in this manner | ||||
| Triplet a,b,c & angle in degrees | prob. from Senkereh | |||
| ref.E.C. Zeeman | from tablet Plimpton 322 |
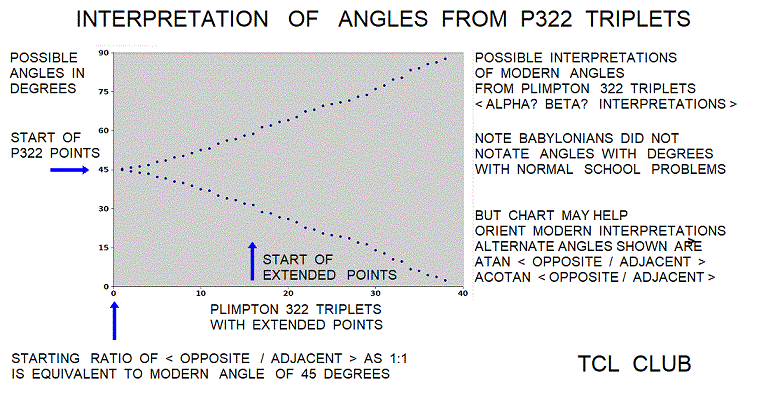
Best guess is that these triplets were used in astronomy and geography. From Zeeman's paper, the triplets imply tangent ratios for angles descending from 44.8 to 31.8 degrees, in modern terms. From the example of the 3:4:5 triangle, the angle would be arctan (3/4) or 37.4 degrees. A few of the triplets seem to suggest latitudes of ancient cities, though not all.
Conjectures on possible uses of triplets.
| quantity | North | East | ||||
|---|---|---|---|---|---|---|
| ancient city | triplet degrees | latitude | units | longitude | units | website |
| akkad | 33.3 | 33.1 | degrees | 44.1 | degrees | http://en.wikipedia.org/wiki/Sumer |
| babylon | 32.536389 | degrees | 44.420833 | degrees | http://en.wikipedia.org/wiki/Sumer | |
| eridu | 31.3 | 30.815839 | degrees | 45.996069 | degrees | http://en.wikipedia.org/wiki/Sumer |
| Hattusa | 40.3 | 40.019722 | degrees | 34.615278 | degrees | http://en.wikipedia.org/wiki/Sumer |
| lagash | 31.41139 | degrees | 46.40722 | degrees | http://en.wikipedia.org/wiki/Sumer | |
| larsa | 31.3 | 31.28583 | degrees | 45.85361 | degrees | http://en.wikipedia.org/wiki/Sumer |
| nippur | 32.12694 | degrees | 45.23083 | degrees | http://en.wikipedia.org/wiki/Sumer | |
| susa | 31.9 | 32.18922 | degrees | 48.257785 | degrees | http://en.wikipedia.org/wiki/Sumer |
| ur | 30.9625 | degrees | 46.10306 | degrees | http://en.wikipedia.org/wiki/Sumer | |
| uruk | 31.32222 | degrees | 45.63611 | degrees | http://en.wikipedia.org/wiki/Sumer | |
| umma | 31.633 | degrees | 45.867 | degrees | http://en.wikipedia.org/wiki/Sumer | |
| building | triplet degrees | slope | units | website | ||
| N. Stone Pyramid,Eygpt | 43.3 | 43.6 | degrees | http://www.kch42.dial.pipex.com/sekes0.htm | ||
| bent pyramid(2),Eygpt | 43.3 | 43.35 | degrees | http://www.kch42.dial.pipex.com/sekes0.htm | ||
| Temple of the Sun,Teotihuacán | 31.9 | 32.494 | degrees | http://en.wikipedia.org/wiki/Pyramid_of_the_Sun |
pseudocode on Babylonian triplets
gold 10/25/2020. The role of Babylonian triplets on Plimpton 322 may be a limited set of Babylonian triplets that satisfy the reciprocal pair relationship under the constraints of the standard Babylonian reciprocal table. A possible constraint was most numbers of triangle sides under sixty. The reciprocal pair relationship as < (X+1/X)**2 - (X+1/X)**2 = 4 > was first identified with geometry and graphical methods to a normalized right triangle. Then the Babylonian mathematicians developed the reciprocal pair relationship with arithmetic methods on the Plimpton 322 tablet. According to Glaisher, the geometric theorem is equivalent to the algebraic identity (a + b)/2 - (a - b)/2 = 4ab and forms Proposition 8. of the second book of Euclid. The Binomial Theorem is a corollary or similar approach. The Binomial Theorem in Euclid II, 4, is formulated as (a + b)**2 = a**2 + 2ab+ b**2, Pascal triangle coefficients <1 2 1>. See Quarter Squares [L1 ] and Triangular Numbers on TCL Wiki [L2 ]
pseudocode on development of Babylonian triplets
# pseudocode on Babylonian triplets
the role of Babylonian triplet on Plimpton 322.
2m, m**2 - 1, m**2 + 1 Babylonian triplet
twin prime number.
twin prime numbers separated by 2,4,6 ...?
c**2= a**2 + b**2
c**2= a**2 + 1 normalized Babylonian triplet
a**2 = c**2 -1 normalized Babylonian triplet
some b and c are both primes on tablet.
some b and c are not both primes on tablet.
The reciprocal pair relationship is key to triplets.
The reciprocal pairs were 2 sides to a normalized right triangle
The reciprocal pair <X-1/X> often seen as initial guess
in Babylonian square root algorithms.
(X+1/X)**2 - (X-1/X)**2 = 4 ,
divide both sides of equation by 4
(1/4)*(X+1/X)**2 - (1/4)*(X-1/X)**2 = 1
normalized triplet, < (1/4)* ((X+1/X)**2 ) , 1 ,(1/4)* ((X+1/X)**2) >
1< X-1/X < 1+sqrt(2) approximate upper limit of ~~ 2.4 in Plimpton 322
The Babylonian regular numbers between 0 and 60 have a limited set of triplets that
satisfy 1< X-1/X < 1+sqrt(2) which appears to be the role of Plimpton 322.
The limit 1< X-1/X < 1+sqrt(2) may explain the 1<X<2 limit
on the some Late Babylonian many place reciprocal tablets.
trial upper limit expr {(180./[pi])*atan(3367./3456)} = 44.25 <line 2>
trial upper limit expr {(1./4)*((30./60+120.)**2)} =3630.0625"
trial upper limit expr {(1./4)*((30./60-120.)**2)} =3570.0625"
trial lower limit from base_60 expr {(1./4)*((2.5+(60./(2.5)))**2)} = 175 rounded
trial lower limit from base_60 expr {(1./4)*((2.5-(60./(2.5)))**2)} = 115 rounded
trial angle formula expr {(180./[pi])*atan(115./175.)} = 33.3 degrees
33.3 degrees is near lower limit on extant Plimpton 322 <line 15>.
d=6 even number, l = divisor of d**2 with integer result, Babylonian triplet method
a= l+b
b= d+ (d**2)//(2*l)
c= d+l+(d**2)/(2*l)
# supposed to work for all even dOther tablets supporting the use of Plimpton 322 triplets.
gold 6/12/2021 update.
The Babylonians did not use algebra notation, modern equation notation, decimal notation, or modern units, so the reader will have to bear some anachronisms in the TCL code and mixed notation of modern, Greek, and Babylonians translations. What the Greeks called the hypotenuse, the Babylonians called the diagonal. The Babylonians called a triangle a peghead or wedge. The Babylonians were primarily looking at the sides of the triangle, and not measuring the modern angles. The “wedge” is defined here as two adjacent sides at a corner, the wedge is a half square or rectangle. The long side ( Greek hypotenuse) is equivalent to the diagonal of a rectangle and the short side ( Greek adjacent or B. width) is equivalent to the short side of a rectangle, in most B. problems. The remaining side is the opposite side O. It is helpful if the Greek hypotenuse or B. diagonal d is normalized as 1, to use Heron’s formula. In the table the first column is the adjacent side or width. In using the table one picks the width derived from normalizing the diagonal to one and the respective sides of the rectangle ( examples, a/d and o/d). For the normalized rectangle, the equation is < adjacent (width) = diagonal (1) * adjacent coefficient >. To return to the original rectangle, the equation is < adjacent (width) = Scale_Factor * diagonal (1) * adjacent coefficient >. For the normalized diagonal using Heron’s formula, the equation for the adjacent side is < opposite side (height) = diagonal (1) - adjacent * adjacent / 2 >. For the normalized diagonal using Heron’s formula, the equation for the opposite side is < opposite side (height) = diagonal (1) - adjacent * adjacent / 2. >. Note that Heron’s formula is considered an approximation of the Pythagorean theorem. The normalized equation for the diagonal side is diagonal (1) = adjacent * adjacent + opposite * opposite >, from the relations developed in the Pythagorean theorem. In the table, the second column or second term may be the < normalized_diagonal / adjacent side >.
Alternate provisional text, update under construction
gold Alternate provisional text, in case laptop zapped, 6/22/2021, update under construction.
About ten years ago, there was a translation paper that was purportedly on a tablet with a table with "Old Babylonian triangle coefficients list". Maybe my memory is wrong, but the gist of the table is carried in the "Wedge" (triangle) coefficients numbers below. I have these numbers in a local spreadsheet too. I wrote something up on my webpage. Maybe, these were really rectangle coefficients? Is there a bibliography of "Old Babylonian coefficients list". There were two similar O.B. tablets about ten years ago. The paper showed the main O.B. tablet with about 16 readable entries, purportedly on triangle coefficients. Maybe, these were really rectangle coefficients similar to the rectangles in the Sumerian metrology listings? It appears the the numbers on the main table were derived from the Heron's formula but that is not certain, as no calculations are shown on the tablet. For now, I do not rule out that some numbers originate with Babylonian triplets on the Plimpton 322 tablet. The paper showed the main O.B.tablet with about 16 readable entries, purportedly on triangle coefficients. I am trying to support the theories of Mansfield & Wildberger on the Plimpton 322 triplets.
The term ukullu (Accadian for fruit) or sa.gal (Sumerian for coefficient ratio) has been associated with dip or run over rise in the math tablets. The term sa means constant or coefficient in Sumerian. The term gal usually means big or great in Sumerian. The term gal.bi may mean “great it's, possessive coefficient ”, meaning great refers to the opposite side of a triangle. The term bi is simply Sumerian for its possessive. The term bi is seen often in UrIII scribal accounts in “its silver” or “its equivalent in kind”. Example from the Kassite kudurrus (boundary stones): se.numun sa 1 (iku) asag 3 (bán) ina ksu gal-ti, partial translation, seeding area ratio coefficient of i iku is 3 ban, absolute from Base_60 = 30 in cubits great, ti = possessive tag or bi. But the use, meaning, and connotation of gal, sa.gal, and gal.bi in the math tablets is not well understood here. Possibly sa.gal means constant or coefficient (sa) to the great (gal) side. In the ukullu definition, the great (gal) side was normalized and set to integer 1 in the ukullu definition. The great (gal) side may refer to modern opposite side of a triangle or long side of a rectangle. The inference here is that the short side of a Babylonian triangle or rectangle refers to the modern adjacent side. So in effect, a tablet line for ukullu might read igi ;45 sa.gal.bi 1;20 ib.sa. The Base_60 inverse of of ;45 or 45/60 is expr {60./45} = 1.333, 1+20/60 >> 1;20 Base_60. Speculation that the gal.bi in the Seleucid inverse reciprocal lines may refer to the modern opposite side of a triangle.
| table 1c. Cuneiform Coefficient ( sa ) Example lines | printed in tcl wiki format | |||||
|---|---|---|---|---|---|---|
| letter | normally, igi “ eye ”, entry number | complement number | Usually = its or am = “it is” | comment, if any | ||
| a | igi | 2 | gal.bi | 30 | am | example, inverse reciprocal line, Old Babylonian text |
| b | igi | 2 | zip | 30 | am | example, inverse reciprocal line, NeoBabylonian text |
| c | igi | 2 | zip | 30 | ib.si | example, inverse reciprocal line, rare, Uruk. An Achaemenid Many-Place Table |
| ib.sa | ib.si or ib.sa, equal sided its, usually only seen on tables of squares and cubes | |||||
| d | igi | 2 | gal.bi | 30 | am | example, inverse reciprocal line, Seleucid text |
Testcases for popular rectangles in Babylon and Egypt
;# It takes about 8 or 9 digits of decimal Base_10
;# to equal the precision of Base_60 on some Babylonian math problems.
;# popular rectangle 1
;# rectangle with width 45/60, length = 1, diagonal = 1+15/60
;# < ;45 1 1_15 > associated triplet in Base_60 notation
;# triplet normalized to opposite side
;# < 45/60 1 1+15/60 > ;# triplet in Base_60 fractions
;# checking normalized triplet with Babylonian diagonal rule
set diagonal_rule1 [expr { sqrt (1.0 +0.577350269**2) }] ;# returns 1.1547005382844386
set diagonal_rule2 [expr { sqrt (1.1547005383792524**2-0.577350269**2) }] ;# returns 1.0
set diagonal_rule3 [expr { sqrt (1.0 +0.577350269**2) }] ;# returns 1.1547005382844386
;# < 0.577350269 1., 1.1547005383792524 > assigned triplet
;# the ukullu or inverse slope of 0.577350269 expr { $adjacent /$opposite }.
;# the short_side or adjacent side was between
;# the triplet 16 = 0.60763888888889 and triplet 17 = 0.5474537037037 on Plimpton 322 extension
;# setting percent errors of short_side 0.577350269 between triplet 16 = 0.60763888888889
;# and triplet 17 = 0.5474537037037 on Plimpton 322 extension
set error5 [ errorx 0.577350269 0.60763888888889] ;# returns 5.2461 percent relative error
set error6 [ errorx 0.577350269 0.5474537037037] ;# returns 5.46102 percent relative error
set average_error_on_2 [ expr { ( $error5 + $error6 ) * 0.5 } ];# returns 5.3535 average percent relative error ;# popular rectangle 2
;# rectangle with width = ;20 , length = ;30, diagonal = 36/60.
;# < ;20 ;30 ;36 > associated triplet in Base_60 notation
;# < 20/60. 30/60. 36/60. > ;# Base_60 fractions
;# < 0.33333333 0.5 0.6 > triplet decimal Base_10
;# triplet normalized to opposite side
;# < 0.66666666 1.0 1.2 >
;# checking normalized triplet with Babylonian diagonal rule
set diagonal_rule1 [expr { sqrt (1.0+0.66666666**2) }] ;#
returns 1.2018504214566617
set diagonal_rule2 [expr { sqrt (1.2018504214566617**2-0.66666666**2) }] ;# returns 0.999999999, rnd to 1.0
set diagonal_rule3 [expr { sqrt (1.0**2+0.66666666**2) }] ;# returns 1.2018504214566617
;# the ukullu or inverse slope was expr { $adjacent /$opposite }.
;# the short_side or adjacent side was between
;# the triplet 13 = 0.67083333333333 and triplet 14 = 0.65592592592593 on Plimpton 322
;# setting percent errors 0.66666666 between triplet 13 = 0.67083333333333
;# and triplet 14 = 0.65592592592593
set error5 [ errorx 0.66666666 0.67083333333 ] ;# returns 0.62500 percent relative error
set error6 [ errorx 0.66666666 0.65592592592593 ] ;# returns 1.63749 percent relative error
set average_error_on_2 [ expr { ( $error5 + $error6 ) * 0.5 } ];# returns 1.1312 average percent relative error ;# popular rectangle 3
;# rectangle with width = ;30 , length = ;52_30, diagonal = 1
;# < ;30 ;52_30 ;60 > associated triplet in Base_60 notation
;# < 30/60. 52/60.+30/3600 1. > ;# Base_60 fractions
;# < 0.5 0.875 1. > ;# Base_10 decimal fractions
;# the ukullu or inverse slope was expr { $adjacent /$opposite }.
;# the short_side or adjacent side
;# of 0.5 was between
;# the triplet 19 = 0.50135802469136 and triplet 20 = 0.4875 on Plimpton 322 extension ;# popular rectangle 4, Tablet IM 67118, also known as Db2-146
;# rectangle with width = 30/60 , length = 1, diagonal = 1+15/60
;# 1;15 means 1 + 15/60 = 5/4 = 1.25 decimal Base_10
;# < 0.5 1 1.25 > associated triplet in Base_10 decimal notation
;# the ukullu or inverse slope was expr { $adjacent /$opposite }.
;# the short_side or adjacent side of 0.5 was between
;# the triplet 19 = 0.50135802469136 and triplet 20 = 0.4875 on Plimpton 322 extension| table 2 Babylonian Rectangles factored out and normalized | printed in tcl wiki format | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| rectangles here compare with line 16 and 23 in Plimpton 322 | |||||||||
| adjacent side | opposite side | diagonal | reduction adjacent side | reduction opposite side | reduction diagonal | normalized adjacent side | normalized opposite side | normalized diagonal | comments, if any |
| 3 | 4 | 5 | 3 | 4 | 5 | 0.7500 | 1.0000 | 1.2500 | 1.3333 1-2-3-4-13-17, atan (4/3) = 53.130 degrees plimpton line 16 in decimal 0.75 1.25 |
| 6 | 8 | 10 | 3 | 4 | 5 | 0.7500 | 1.0000 | 1.2500 | 1.3333 9 |
| 9 | 12 | 15 | 3 | 4 | 5 | 0.7500 | 1.0000 | 1.2500 | 1.3333 12 |
| 15 | 20 | 25 | 3 | 4 | 5 | 0.7500 | 1.0000 | 1.2500 | 1.3333 18-19 |
| 32 | 60 | 68 | 8 | 15 | 17 | 0.5333 | 1.0000 | 1.1333 | 1.8750 5-6 atan(15/8) = 61.9275 degrees, Plimpton 322 line 23 in decimal 0.53333333 1.13333333 |
| 8 | 15 | 17 | 8 | 15 | 17 | 0.5333 | 1.0000 | 1.1333 | 1.8750 10-15 , Plimpton 322 line 23 in decimal 0.53333333 1.13333333 |
;# popular rectangle 5, <10 40 41_15> VAT 6598 #6&7, given answer 41_15
;# rectangle with width = 10/60 , length = 40 , diagonal = 41+15/60 in implied Base_60 fractions
;# ratio of length to width is 40/10 or 4:1
;# < 10/60 40/60 41/60 + 15/3600 > in implied Base_60 fractions
;# 1;15 means 1 + 15/60 = 5/4 = 1.25 decimal Base_10
;# < 0.5 1 1.25 > normalized triplet in Base_10 decimal notation
set diagonal2 [ expr { sqrt ( 0.16666666**2 + 0.66666666**2 ) } ] ;# 0.6871842628517559
set conversion_decimal2 [ expr { 0.68718426* 60. } ] ;# 41.2310556
;# the ukullu or inverse slope was expr { $adjacent /$opposite }.
;# the short_side or adjacent side of 0.5 was between
;# the triplet 19 = 0.501 and triplet20 = 0.4875 on Plimpton 322 extension19
;# setting percent errors of short_side .5 between triplet 19 = 0.501
;# and triplet20 = 0.4875
set error5 [ errorx .5 0.501 ] ;# returns 0.2000 percent relative error
set error6 [ errorx .5 0.4875 ] ;# returns 2.5641 percent relative error
set average_error_on_2 [ expr { ( $error5 + $error6 ) * 0.5 } ];# returns 1.38205 average percent relative error ;# Usage example of errorx as one liner program
;# in finding percentage errors and average of errors.
;# The ukullu or inverse slope
;# was expr { triangle side $adjacent/ side $opposite }.
;# The adjacent side or triangle short side was between
;# the triplet 19 = 0.501 and triplet 20 = 0.4875 on Plimpton 322 extension
;# setting percent errors of triangle short side .5 between triplet 19 = 0.501
;# and triplet20 = 0.4875
set error5 [ errorx .5 0.501 ] ;# returns 0.2000 percent relative error
set error6 [ errorx .5 0.4875 ] ;# returns 2.5641 percent relative error
set average_error_on_2 [ expr { ( $error5 + $error6 ) * 0.5 } ];# returns 1.38205 average percent relative errorIn the Seleucid problem 34568P1, the scribe computes the diagonal without using the Pythagorean theorem. The scribe did not explain the theory behind the problem 34568P1. At first glance to the modern reader, the tablet appears to be an "a priori" solution or knowledge out of the sandbox. But there are two alternate methods tha thave been proposed in modern dress and may be developed into a TCL subroutine. Following discussion relined heavily on references Neugebauer, Friberg, and Gonçalves. But the discussion here uses modern notation and terminology.
The problem is based on the famous < 3 4 5 > triangle, where two sides are introduced as given as 3 and 4, and the answer given as 5. The scribe uses the formula in as expr { 3 + (1/2.) * 4 }, returns 5. Not on the tablet, but a similar solution is expr { 4 + (1/3.) * 3 } , returns 5. Gonçalves and maybe Gillings found that the problem could be solved by reformulating the problem as a quadratic equation. The quadratic equation was < t**2 + 2*(3/4) -1 = 0 ., where the positive solution was K1 = 1/2. The alternate quadratic equation was < t**2 + 2*(4/3) -1 = 0 > , where the positive solution was K2 = 1/3. Up to now, we have + K1 * opposite_side = diagonal. Also, opposite_side + K2 * adjacent_side = diagonal.
Off the tablet, the Babylonian math gives some linear relationships on normalized triangles for inverse reciprocals in Base_60. The relation (1/2) + (1/2)* $igum = 3/4>. With transposition, < (1/2) * $igum = (1/4). Then $igum = (1/2) = K1, the transformation constant that we are looking for. The alternate relation (1) + (1)* $igum = 4/3>. With transposition, < $igum = (4/3) - 1. .Then '$igum = (1/3) = K2.
#; Eratosthenes' method to calculate the Earth's circumference has been lost.
#; Original units were greek_stadia which are converted to meters here.
#; 1 greek_stadium (Egyptian unit) is equal to 157.5 meters
set greek_stadia_length [ expr { 5000.0 * 157.5 } ] ;# returns 787500.0 meters
set earth_circumference [ expr {360.0 * 787500.0 / 7.2 } ;# returns 39375000.0 meters , convert to 39375. kilometers
set earth_circumference_error [ errorx 40076.0 39375. ] ;# returns 1.78 percent low
#; converting to Babylonian units, 1 beru (double march ) equals 10.8 km.
set beru_length [ expr { 787.5 / 10.8 } ] ;# returns 72.9166 beru
set earth_circumference_in_beru [ expr {360.0 * 72.9166 / 7.2 } ] ;# returns 3645.830 beru
set difference_earth_circumference_Eratosthenes [ errorx 3600.0 3645.830 ] ;# returns 1.2730 percent low
;# proportions 6 / 360 = 60 / $circumference, $circumference = 360 * 60 / 6.
set sumerian_circumference [ expr { 360. * 60. / 6. } ] ;# returns 3600 beru
set gilgamesh_altitude [ expr { 24* 10.8 } ] ;# returns 259.2 km
set gilgamesh_voyage_ref_earth_circumference [ expr { 120 * 10.8 } ] ;# returns 1296.0 kmThe hand techniques that the Babylonian Astronomers used to measure sky angles is not well known to the later amateurs. However, the Babylonian Astronomy diaries record the angular measurements of stars in cubits and susi. In some older tablet translations, susi are translated fingers. There are either 20 or 24 susi in a cubit depending on the era of the tablet. The clay tablets also record some calculations using Us < literally water (weight measure) > or "4 minutes of time". An Us or one unit of the water clock is equivalent to one modern degree of angle. One cubit in the sky for celestial angles is equivalent to 2 Us or 2 degrees. Using proportions, a Babylonian susi or finger might be about (1 cubit)/(24 susi)*(2 degrees) / (1 cubit) or expr { (1./24.)*(2./1.} or 0.083 degree. 6 fingers would be expr (1./24.)*(2./1. )*6.} or 0.5 degrees. One finger would be expr { (1./24.)*(2./1. )*1.}, returns 0.083 degrees. The Babylonian Astronomy diaries record distances of planets from fixed stars along the Zodiac to one finger and some tablets record 1/2 or 1/3 fingers. Based on testimony in the Babylonian Astronomy diaries, believe that Babylonian Astronomers could detect errors of at least 1 percent in the Mul Apin star chart for area of Babylon.
The only known math problems contemporary to Hammurabi of Babylon, that might require the accuracy of the proposed Mansfield & Wildberger ratio geometry on the Plimpton 322 triplets, would be 1) correction of the star chart to the latitude of Babylon and 2) possible map making and ship charts. The linguists seem adamant that the extant Babylonian "scribe school" problems would not require the accuracy of the Plimpton 322 triplets as a ratio geometry. However, leaving the Babylonian "scribe school" problems aside, there is something about the Mul Apin star charts that indicate some kind of angle concepts, but the evidence of the Mul Alpin star charts are at least a thousand years later than Hammurabi. I am searching for a more diplomatic way to put these issues.
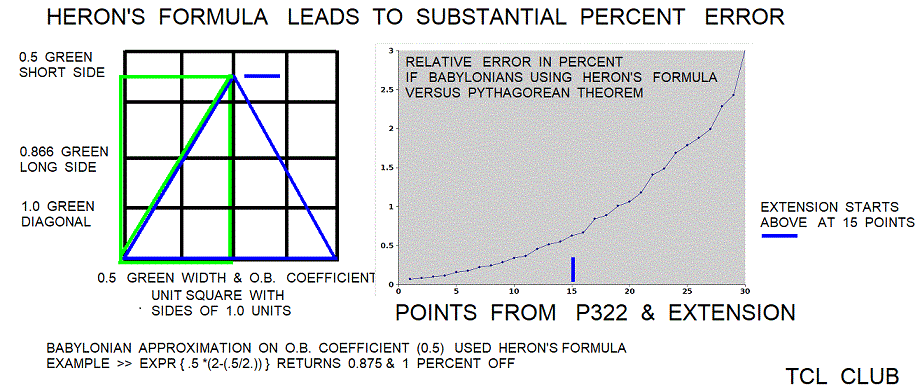
Relations of Heron’s law
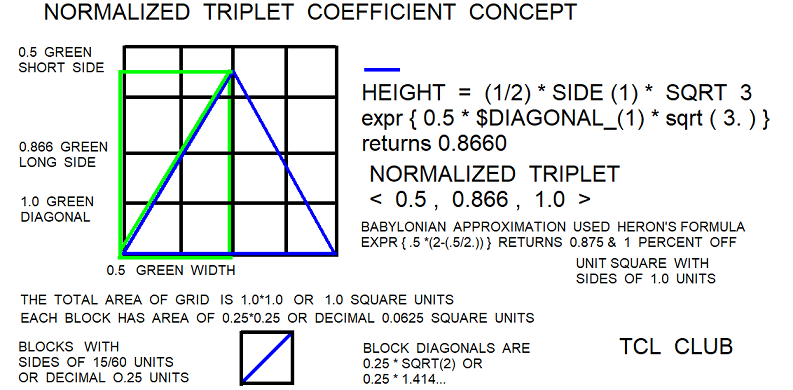
Lets try a testcase from the tablet using the relations of Heron’s law. The adjacent side is ;30 Base_60 fraction or 0.5 decimal, opposite side is expr { 52/60. + 30/3600} = 0.875 given elsewhere, second column is 2, and the diagonal is the normalized 1. We calculate the opposite side using the second column and develop relations using Heron’s law. These are three alternate methods of calculating the height of the triangle. Opps! I almost wrote height of pyramid. The Pythagorean_theorem for opposite side is set pythagorean_theorem_height [expr { sqrt (1**2-.5**2)} ;# returns 0.8660 rnd. The formula for the height of an equilateral triangle is expr { 0.5 * $DIAGONAL_(1) * sqrt ( 3. ) }, 0.8660. Heron’s law is approximation formula expr { .5 *(2-(.5/2.)) }, 0.875. The one line error proc is set percent_error < errorx 0.875 0.8660> ;# returns 1 percent error rounded. There are isolated instances of cuneiform coefficients for opposite side in the tablets, but I have not found an organized table of coefficients for opposite side per se.
;# derivation for opposite side
< opposite side (height) = diagonal (1)- adjacent * adjacent / 2.>.
< opposite side (height)/ adjacent = diagonal (1)/adjacent - adjacent * adjacent / 2./adjacent >.
< opposite side (height)/ adjacent = diagonal (1)/adjacent - adjacent / 2.>.
< normalized opposite side (height) = adjacent * < col2 - adjacent / 2. >
;# opposite side (height) = expr { .5 *(2-(.5/2.)) } = 0.875
;# from one line programs in compendium
;# comparing accuracy of Heron_method and pythagorean_theorem for opposite side
set heron_method [ expr { .5 *(2-(.5/2.)) } = 0.875 ] ;# returns 0.875
set pythagorean_theorem_height [expr { sqrt (1**2-.5**2) } ;# returns 0.866025403784438 for opposite side
proc errorx {aa bb} {expr { $aa > $bb ? (($aa*1.)/$bb -1.)*100. : (($bb*1.)/$aa -1.)*100.}}
set percent_error [ errorx 0.875 0.866025403784438] ;# returns 1 percent error rounded
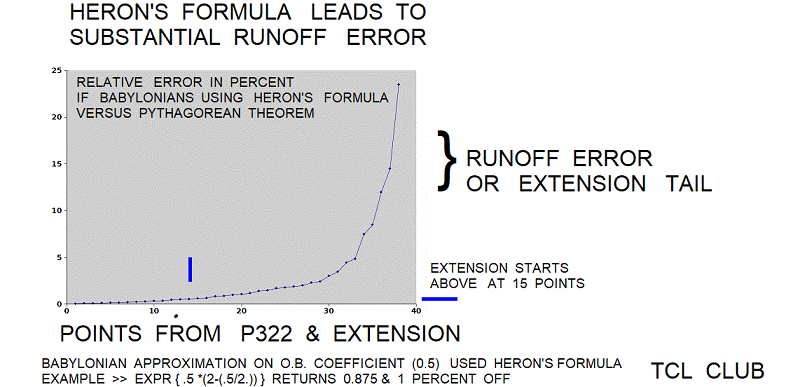
There are some similarities or coincidences between the table and Plimpton 322. The Table of Wedge and Triangle Coefficients has 16 extant entries between 45 and 5.7 degrees. In the extant entries, Plimpton 322 has a list of 15 different right triangles with angle in the range of 30 to 45 degrees. The tablet has lines giving a relationship between the short side of a normalized right triangles and rectangles and the ratio of < diagonal / short_side >. In some interpretations, Plimpton 322 gives a relationship between the short side of a normalized right triangles and rectangles, the ratio of < short_side / factor_n > **2, the ratio of < diagonal / factor_n > **2, but there are regular base_60 factors in the denominators. Subject to off tablet implementation and interpretation, both methods may be trying to avoid taking square roots, but are taking squares to generate the output numbers. The Heron method is taking the hypotenuse as 1 in ref Eleanor Robson, whereas the Plimpton 322 method is setting the opposite side as 1, reference interpretation of Mansfield & Wildberger Maybe numerical coincidence, but the Table of Wedge Coefficients has some evidence that the table or coincident coefficient numbers are being used or quoted in both O.B. coefficient lists and O.B. math problems. From the work of numerous authors, the Plimpton 322 is more sophisticated and more work for the scribe to complete, by several orders of magnitude. Plimpton 322 is a Babylonian clay tablet that is believed to have been written about 1800 BC. The understanding here is that Table(s) of Wedge and Triangle Coefficients supports the ratio based geometry theory of Mansfield & Wildberger, in the sense that the Table(s) of Wedge and Triangle Coefficients may be an earlier or different version based on the Heron's theory before < b**2 + l**2 = d**2 > was formalized in Plimpton 322.
The key to the wedge coefficients is correct Babylonian triplets with the Pythagorean relationship. Once the set of correct Babylonian triplets are prepared, the “scribe” can prepare a wedge coefficient (sa-gal) for the adjacent or opposite sides of a single triangle or multiple for a table of wedge coefficients on multiple triangles. The modern scribe may either use the Heron’s method or the Pythagorean method to prepare the wedge coefficients from the set of correct Babylonian triplets. Note that Heron’s formula is considered an approximation of the Pythagorean theorem. Heron’s formula is giving about 1 percent error here from the Pythagorean theorem. The approximation error in Heron’s formula may have been the reason that Plimpton 322 was developed about the reign of Hammurabi for more accurate wedge coefficients. One should not rule out interpolation between the existing wedge coefficients or other uses for the Babylonian triplets than to prepare a table of wedge coefficients.
Subtitle Gradient Coefficients. In the Old Babylonian coefficient tables, the 7 readable gradients in a set are 1/7, 1/6, 1/5, 1/4, 1/3, 1/2, and 2/3. There are unreadable lines before and after the set of readable gradients. On the same tablet, there are readable lines that have 1/1 sides for a square. In other texts, there is a math problem that calls for a 1 cubit vertical decline in a cubit horizontal distance (1/1), equivalent to a tangent angle of 45 degrees. So its probably safe to add the 1/1 ratio at equivalent 45 degrees to the table of standard gradients.
Conclusions
With the uncertainty of dating clay tablets, it is difficult to say that one method of solving triangles came before another. However, the poor accuracy in Heron's method suggests that the Plimpton 232 was an attempt to the improve Babylonian method of solving triangles with Babylonian triplets . However, Heron's method continued to be taught on the extant school tablets and passed on to the later Greek mathematicians. So there appears two possible methods for solving a right triangle, either Heron's Method or using the nearest normalized Babylonian triplets. But I am not sure the linguists would buy off on this or could find unquestionable examples in the texts. Another possibility is to interpolate between two normalized Babylonian triplets that bracket the solution and interpolate.
*
*
"Wedge" (triangle) coefficients for cuneiform math from clay tablets
Example formula from tablets: 1 kus 15 sa.gal >> [in] one cubit 15 [is the] slope.
Usually less revealing or broken off text:
15 igi.gub >> 15 [is] reciprocal coefficient .
The clay tablet(s) include redundant terms in different expressions,
usually in reciprocal values.
Note: This content and sources are buried deep in the internet "stacks".
MCT and other tablets have been put behind a firewall and paywalls,
such that I doubt a regular search engine could pull this content, as formerly.| combined table from two tablets for ukullu or inverse slope , includes modern calculated columns | printed in | tcl wiki format | ||||
|---|---|---|---|---|---|---|
| first tablet | >>>>> modern assumed & calculated columns after first 2 columns | |||||
| short_side coeff. in sexagesimal | ukullu or inverse slope in fractions (opposite_side / adjacent side) | big assumption, normalized_opposite_side (1) | degrees | cotangent ratio | decimal tangent | comments, if any |
| 1; | 1 | 1 | 45.0 | 1.0 | 1. | unreadable first entry, but likely content |
| 0;30 | 2 | 1 | 26.56 | 2. | 0.5 | |
| 0;20 | 3 | 1 | 18.43 | 3. | 0.333 | |
| 0;15 | 4 | 1 | 14.04 | 4. | 0.25 | |
| 0;12 | 5 | 1 | 11.309 | 5. | 0.2 | |
| 0;10 | 6 | 1 | 9.462 | 6. | 0.1666 | |
| 0;09 | 7 | 1 | 8.130 | 7. | 0.142 | |
| 0;08 | 8 | 1 | 7.125 | 8. | 0.125 | |
| 0;07 | 9 | 1 | 6.340 | 9. | 0.111 | |
| 0;06 | 10 | 1 | 5.710 | 10. | 0.1 | |
| begin unreadable lines on first tablet | possibly 16 lines believed missing | |||||
| second tablet | >>>>> modern assumed & calculated columns after first 2 columns | |||||
| short_side coeff. in sexagesimal | ukullu or inverse slope in reciprocals? (1/opposite_side / adjacent side) | big assumption, normalized_opposite_side (1) | degrees | cotangent ratio | decimal tangent | comments, if any |
| 0;09 | 1/7 | 1 | 8.130 | 7. | 0.142 | ukullu appear reciprocals? |
| 0;10 | 1/6 | 1 | 9.462 | 6. | 0.1666 | similar value on first tablet |
| 0;12 | 1/5 | 1 | 11.309 | 5. | 0.2 | similar value on first tablet |
| 0;15 | 1/4 | 1 | 14.036 | 4. | 0.25 | similar value on first tablet |
| 0;20 | 1/3 | 1 | 18.435 | 3. | 0.333 | similar value on first tablet |
| 0;30 | 1/2 | 1 | 26.565 | 2. | 0.5 | similar value on first tablet |
| 0;40 | 2/3 | 1 | 33.690 | 1.5 | 0.666 | value not on first tablet |
| begin unreadable lines on second tablet | possibly 16 - 20 lines believed missing |
- Otto Neugebauer, Keilschrifttexte, Berlin: Springer, 1935/37, in German
- Otto Neugebauer & Abraham Sachs, Mathematical Cuneiform Texts, 1945, in English
- Table YBC7243 in Yale, referenced in MCT 136 , Neugebauer, Otto E. & Sachs, Abraham J., 1945
- Mesopotamian mathematics, Eleanor Robson, Published 2007
- ASH1922.168, ;30 quoted three times.
- rule of Heron, ref BM96957 and Vat6598.
- Eleanor Robson & D. Fowler, Square root approximations
- in Old Babylonian mathematics: YBC 7289 in context
- Anne Draffkorn Kilmer, Two New Lists of Key Numbers for Mathematical Operations,
- 1960 , 273–308
- Youtube, Old Babylonian Mathematics and Plimpton 322: How did the OB scribe construct P322?
- above from Daniel F. Mansfield , N.J. Wildberger.
- Old Babylonian Mathematics and Plimpton 322
- above from Daniel F. Mansfield , N.J. Wildberger.
- Pythagorean Triads in Babylonian Mathematics, E. M. Bruins
- Three Old Babylonian Methods for Dealing with "Pythagorean" Triangles,
- Eleanor Robson, Journal of Cuneiform Studies
- cojs.org/tell_harmal_mathematical_tablets, Tell Harmal Mathematical Tablets
- cojs.org/polygon_tablet
- cojs.org/mathematical_cuneiform_tablet-_19th_century_bce
- IM 67118, also known as Db2-146, concerning a rectangle with given area and diagonal.
- critical dated tablet, I think
- dates to approximately 1770 BCE (according to the middle chronology)
- during the reign of Ibal-pi-el II of Eshnunna
- at the same time that Hammurabi ruled Babylon.
- similar to Problem 2 on the tablet MS3971 in the Schøyen collection
- similar to Hebrew manual from 1116 CE, link to Jewish Math scholars!
- en.wikipedia.org/wiki/YBC_7289
- tablet ASH 1922.168, 3 occurrences of triangle coefficients , ( ;30 ), refers to short side ( modern adjacent side) of half equilateral triangle
- tablet AUAM 73.2834, 1 occurrence of triangle coefficient , ( ;30 ) , refers to short side ( modern adjacent side) of half equilateral triangle
- following based on Robson's coefficient paper.
- triangle coefficient , ( ;26_15 ) refers to area of half equilateral triangle
- triangle coefficient , ( ;52_30 ) refers to long_side ( modern opposite side) of half equilateral triangle
- triangle coefficient , ( ;7_30 ) possibly refers to lack or complement of long_side, ref height of equilateral triangle
- long_side ;52_30 = diagonal(1) - ;7_30, decimal
- triangle coefficient , ( ;57_36 )
- triangle coefficient , ( ;30 ) refers to (1/2) of modern triangle area formula, area = expr { (1/2.) * short_side * long_side}
- triangle coefficient , ( 1 ) refers to normalized diagonal of half equilateral triangle
- cane against a wall problem of BM 34568:12
- log against a wall problem of BM 85196:9
- Bruins and Rutten 1961, 114-117; ref trapezoid partition problems
- Vaiman, 1955, 72; ref trapezoid partition problems
- Friberg, 1980a, 421. ref trapezoid partition problems
- Gandz, 1938, 4561.
- right angle triangle problem text, BM 34568.
- R. J. Gillings, The Australian Journal of Science, 26, (1964) pp. 225-6.
- AO 6456. Published in Neugebauer ,1935–1937, I, 14,
- AO 6484. Published in Neugebauer ,1935–1937, I, 96,
- BM 34 568. Published in Neugebauer ,1935–1937
- Plimpton 322. Published in Neugebauer and Sachs ,1945, 38,
- VAT 7848. Published in Neugebauer and Sachs ,1945, 141,
- YBC 6967. Published in Neugebauer and Sachs ,1945, 129,
- YBC 7289. Published in Neugebauer and Sachs ,1945
- UET 7-114 and UET 7-115 , called the table of lengths ,
- and the second table was called‘‘table of heights’
- An alternative to the Pythagorean rule?
- Reevaluating Problem 1 of cuneiform tablet BM 34 568
- Carlos H.B. Gonçalves
- DeSegnac, MS 3908 A RE-CONSTRUCTION, D.A.R. DeSegnac
- A draft for an essay
- DeSegnac, MENTAL COMPUTING OF THREE ARCHAIC
- MESOPOTAMIAN PUZZLES W 20044, 35, W 20044, 20 & W 20214, essay draft
- DeSegnac, HARMONY OF NUMBERS I and II, D.A.R. DeSegnac, A draft for an essay
- plimpton 322: a universal cuneiform table
- for old babylonian mathematicians,
- builders, surveyors and teachers
- Rudolf Hajos, really good and understandable
the reciprocals solving rectangle algorithm
:# pseudocode on the reciprocals solving rectangle algorithm
ref Carlos Gonçalves, Universidade de São Paulo on BM 34568P1
rectangle is short side = 3 and long side = 4
solve for diagonal given as 5
solve quadratic equation t**2 + 2*(3/4)*t − 1 = 0.
solution t = 1/2
solve quadratic equation t**2 + 2 · (4/3) * t − 1 = 0.
solution t = 1/3
set diagonal expr { 3+(1/2.)*4.} ; returns 5
set diagonal expr { 4+(1/3.)*3.} ; returns 5
solving for (1/2) difference between reciprocal pairs
< C C_> in B. reciprocal table.
normalize short_side and long_side by 1/(long_side)
normalized set is now < 0.75 1.0 XXX >More inverse pairs of reciprocals
Another issue was the Babylonian tables of reciprocal or inverse numbers. This paragraph relies heavily on Melville's paper referenced below. In the Babylonian 60 base system, pairs of numbers like 2:30 have a product of 60 in base 10 and a product of 1 in base 60. Some inverse pairs are easy to remember and some are not. Some easy inverse pairs are 2:30,3:30,4:15,5:20;6:10,10:6. The Babylonians seem to have used these inverse tables for multiplication like the logarithm tables were used before the computer.
If one looks at the easy pairs found, there is an algorithm that would find some more inverse pairs. For example, a double operation on 2:30 of doubling the first number and having the second would produce would produce 4:15. Lets express the operation in pseudocode as
pseudocode on finding more inverse pairs of reciprocals
pseudocode: 2*$first:$second*1/2.
pseudocode: set first 4 ;
set second 15;
set salty 3
set i 0
while {$i <= $salty} {
set first [>2.*$first];
set second [>$second*(1./2.)]
if { [expr {1.*$i} ] >= $salty} { break }
incr i 1;};#endFor the pair 4:15, the operation would produce 4:15 > alg. > 8:7+1/2 (base 10). In base 60, the Babylonian would write this new pair in fraction of base 60 as 8:7+30/60. However the Babylonian would not use punctuation, but would use blanks and implied fractions, something like 8 blank 7 blank 30 . In the first column of the clay tablet, there are numbers separated by blanks ( and broken off in some spots).
Of particular note is the Babylonian triplet 12709:13500:18548 Maybe, numerical coincidence, but the diameter of the earth at the poles is 12,756.1 km. Diameter of the earth at the equator is 12713.5 km. On occasion, the Sumerians used length units that seem equivalent to the meter and 10 kilometers. The step unit or sepu was equal to one meter. The Sumerians used unit of distance called a beru which was about 10.8 km, so some of the Sumerian measurement units were multiples of the kilometer. Earth's circumference between N&S poles is (40,008 km), as a km is defined... Makes one think about what the Babylonians were measuring?
After looking at the Babylonian clay map, it was not too obvious how the circle overlapped the acute heptagon. There was one construction where the width of the do-nut seems to equal the diameter of the original circle. Anyway a "four leaf clover oriented + " was tried and seemed to work.
Trying to find some earlier estimates of earth's circumference from other cultures. Most of the early constants were given underived without sources. Scanty sources and circular reasoning , no good text reference, speculates that the Sumerians might have used 3600 beru as circumference, with the earth circumference as 3600*10.8 km. Given ~, the earth radius would be 573 beru 9_33,base 60) and diameter would be 1146 beru (19_6,base 60). From modern estimates, terminology, and results, one degree of latitude equals expr { 113./10.8 } 10.5 beru. Still trying to find out if "miles" on clay tablet BM 92687 are beru or else.
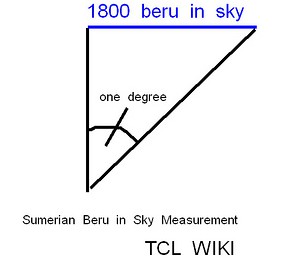
set sumerian_earth_circumference [ expr { 3600 * 10.8 } ] ;# returns 38880.0 kilometersOn Sumerian clay tablet, there are 655200 "beru ina sama" summed up, akkadian for "beru in sky." This factors to 364*60*30. There are 86400 seconds in a day. There are 655200 beru in sky over 360 conventional degrees or 1820 per degree. The apparent disk of sun or moon was supposed to be 1000 beru (~to 0.5 degree). In conventional astronomy, a degree contains 60*60 or 3600 arcseconds. So a beru in sky may something like a double second (meaning double arcsecond). In modern constants, a double arcsecond would be equivalent to 1800/111.3km or 16.17 double arcseconds per km ( from one latitude degree equals 111.3 km). A sky triangle of one degree and an opposite side of 1800 would have a side of 1800/tan(1) or 103137.638. A second and almost equal side would be 1800/sin(1) or 103121.93. considerations for circle, 360*60*60=1296000 364*60*60=1310400, say 1310400/2=655200.
Arithmetic Classic of the Gnomon and the Circular Paths of Heaven reported triplet as follows.
| 60000 li | 24948 km | 15502.2 miles |
| 80000 li | 33264 km | reputed altitude of sun |
| 100000 li | 41580 km | reputed distance from measuring stick to sun |
The Chinese li unit of distance was 0.4158 km (0.25837 miles). 2* babylonian 12709 =25418 Chen Zi of first century reported indirect numbers leading to earth diameter of 911489 li or 378997km. Still trying for original text, but it seems his li in the text has a factor of ten involved. Can only suggest Chen Zi's number for the earth circumference was 37900. km and implied constant was 105.27 km per degree, in modern terms. Eratosthenes third century BCE 46250 km Ptolemy c140CE 28800 km The giant of Chinese legend Pan Gu (or panku, ancient basin) held the earth and sky apart at 90000 li (45000 km). The Egyptians held that the N/S length of Egypt was 1/50 of the globe circumference. The Romans use 75 roman miles as eq to one degree of latitude. The Mogul era "Ain" states the earth's circumference was 8000 farsakh(1600CE). In some texts of Aryabhatiya, the diameter of the earth is mentioned as 3300 yojanams. Brahmagupta ( 7th c) wrote that the circumference of the earth was 36,000 km, in modern units.
The report button calls the eTCL console and adds some functions for inscribed circle. For testing, the triplet 3:4:5 has an inscribed circle of radius one. The radius one is useful for checking common sphere and volume formulas since the number pi or multiples show obviously in the answer. Most of my functions repeat the input to be sure data being transferred correctly to procedures. Its always advisable to check at the low and high end of the expected inputs. The sphere of radius one is the low end. The big kahuna on the clay tablet was 12709:13500:18548 **console session** & The cir function take the three sides of a Babylonian triplet and returns various parameters of the triplet and inscribed circle. The form is cir aa bb cc.
Triplets & Inscribed Circles
eg. cir 3 4 5
1% cir 3 4 5
3 side 1
4 side 2
5 side 3
1.0 radius on inscribed circle
2.0 if available, diameter of circle
6.283185307179586 if a., circumference of circle
3.141592653589793 if a., area of circle
4.1887902047863905 if a., volume of sphere
12.566370614359172 if a., surface area of sphere
3% cir 12709 13500 18548
12709 side 1
13500 side 2
18548 side 3
3833.399264743218 radius on inscribed circle
7666.798529486436 if available, diameter of circle
24085.957936787614 if a., circumference of circle
46165546.72275886 if a., area of circle
235961297151.32327 if a., volume of sphere
707883891453.97 if a., surface area of sphere Conclusions
gold 6/12/2021 updated
The key to the wedge coefficients is correct Babylonian triplets with the Pythagorean relationship. Once the set of correct Babylonian triplets are prepared, the “scribe” can prepare a wedge coefficient (sa-gal) for the adjacent or opposite sides of a single triangle or multiple for a table of wedge coefficients on multiple triangles. The modern scribe may either use the Heron’s method or the Pythagorean method to prepare the wedge coefficients from the set of correct Babylonian triplets. Note that Heron’s formula is considered an approximation of the Pythagorean theorem. Heron’s formula is giving about 1 percent error here from the Pythagorean theorem. The approximation error in Heron’s formula may have been the reason that Plimpton 322 was developed about the reign of Hammurabi for developing more accurate wedge coefficients. The understanding here is that Table(s) of Wedge and Triangle Coefficients supports the ratio based geometry theory of Mansfield & Wildberger, in the sense that the Table(s) of Wedge and Triangle Coefficients may be an earlier or different version based on the Heron's theory before < b**2 + l**2 = d**2 > was formalized in Plimpton 322. One should not rule out interpolation between the existing wedge coefficients or other uses for the Babylonian triplets than to prepare a table of wedge coefficients.
Screenshots Section
figure 1.
figure 2a.
figure 3a. Babylonian world map
Ref. en.wikipedia.org/wiki/Babylonian_Map_of_the_World
1. possibly refers to Dilman (modern Bahrain) and Magan (modern Oman)
2. possibly refers to Egypt
5. possibly refers to Northern land of cold and darkness
7. possibly refers to India
figure 3b. geometric paste up, Babylonian world map
figure 4a.
figure 4b.
tangent angle differences in degrees from triplets
figure 5.
alternate star
figure 6.
possible construct for Babylonian world map
6/22/2021, update under construction
figure 7. Babylonian_Triplets_ full tablet extension
figure 8. Babylonian_Triplets_percentage_error
figure 9. Babylonian_Triplets_heron_formula
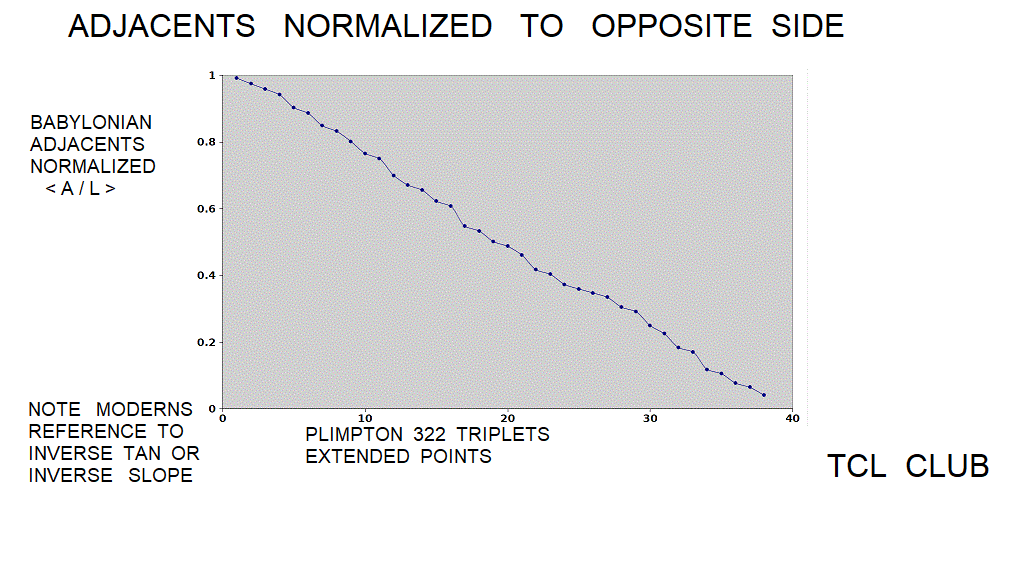
figure 10. Babylonian_Triplets Adjacent sides normalized to opposite sides
Adjacent sides are normalized to opposite sides with Plimpton 322 Extension points added.
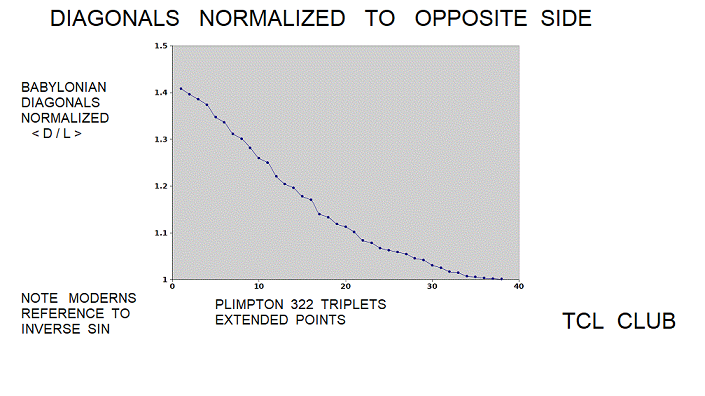
figure 11. Babylonian_Triplets Diagonals sides normalized to opposite sides
Diagonals sides are normalized to opposite sides with Plimpton 322 Extension points added.
figure 12. Possible interpretations of Babylonian_Triplets_angles
figure 13. Console helper for normalized_set of Babylonian_Triplets
figure 14. Searching for Babylonian Triplets equilateral triangle
figure 15 . Searching for Babylonian Triplets diagonal rule
References:
- Methods and traditions of Babylonian mathematics: Plimpton 322,
- Pythagorean Triples, and the Babylonian Triangle Parameter Equations
- Author(s): Jöran Friberg
- Title: The Babylonian “Pythagorean Triangle” Tablet
- Author(s): DEREK J. DE SOLLA PRICE
- Wiki page Math proc templates for Prime Number generation and TCL demo example, numerical analysis
- Book: Lost Discoveries: The Ancient Roots of Modern Science
- Daniel F. Mansfield , N.J. Wildberger.
- Plimpton 322 is Babylonian exact sexagesimal trigonometry.
- Historia Mathematica, August 2017 DOI: 10.1016/j.hm.2017.08.001
- Newsweek, Babylonian Tablet Could Hold Mathematical
- Secrets For Today's Researchers, Josh Lowe , 8/25/17
- Pythagorean triple
- Yale Catalog Number: YPM BC 019086, Coefficient list--mathematical text.
- Original Number: YBC 05022
- Department: Anthropology: Babylonian Collection
- Tablet. Coefficient list--mathematical text. Old Babylonian. Clay. Numeral 8 written on 2 tiers.
- Catalog Number: YPM BC 021308
- Original Number: YBC 07243
- Department: Anthropology: Babylonian Collection
- cited CMT 279 (bibliography for coefficient lists; primary publication: MCT pl.18 (
- CMT 278-279
- Apastamba's rules give Pythagorean triples from Shulba Sutras
- (3,4,5)
- (5,12,13)
- (8,15,17)
- (12,35,37)
- Baudhayana in Baudhayana Shulba sutra
- rectangle 3 and 4, implies triplet < 3 4 5 > , expr sqrt (3**2+4**2) ;# returns 5.0
- rectangle 12 and 5,implies triplet < 5 12 13 > , expr sqrt (12**2+5**2) ;# returns 13.0
- rectangle 15 and 8,implies triplet < 8 15 17 > , expr sqrt (15**2+8**2) ;# returns 17.0
- rectangle 7 and 24, implies triplet < 7 24 25 > , expr sqrt (7**2+24**2) ;# returns 25.0
- rectangle 12 and 35, implies triplet < 12 24 25 > , expr sqrt (12**2+35**2) ;# returns 37.0
- rectangle 15 and 36. implies triplet < 15 36 39 > , expr sqrt (15**2+36**2) ;# returns 39.0
appendix TCL programs and scripts
Slot_Calculator
Pretty Print VERSION
# pretty print from autoindent & ased editor
# searching for Babylonian triplets
# code from TCL WIKI Slot_Calculator_Demo
# 6Aug2010, [gold]
package require Tk
proc positionWindow w {
wm geometry $w +300+300
}
set font {Helvetica 18}
set colorgrd seashell4
set colorback bisque
set colorwarning tomato1
frame .frame -relief flat -bg aquamarine4
pack .frame -side top -fill y -anchor center
set names {{} {guess N:} {not used:} {not used:} {side1:} {side2:} {side3:} possible:}
foreach i {1 2 3 4 5 6 } {
label .frame.label$i -text [lindex $names $i] -anchor e
entry .frame.entry$i -width 35 -textvariable side$i
grid .frame.label$i .frame.entry$i -sticky ew -pady 2 -padx 1
}
proc about {} {
set msg "Calculator for Searching Babylonian Triplets.
from TCL WIKI"
tk_messageBox -title "About" -message $msg
}
proc pi {} {expr acos(-1)}
# 5 = 22 + 12, 13 = 32 + 22, 5 : 12 : 13,
proc tripletxxx { xx1 yy1 xx3 yy3 xx2 } {
global side4 side5 side6
set max 1
set salty [expr {$xx1 + 5.}]
set i 2
while {$i <= $salty} {
set max $i
if { [expr {2.** $i} ] <= $xx1} { set power2 [expr {2**$i}] }
if { [expr {3.** $i} ] <= $xx1} { set pow2 $i }
if { [expr {2.** $i} ] >= $xx1} { break }
incr i 2
}
set max 1
set j 0
while {$j <= $salty} {
set max $i
if { [expr {3.** $j} ] <= $xx1} { set power3 [expr {3**$j}] }
if { [expr {3.** $j} ] <= $xx1} { set powerx [expr {2**$j}] }
if { [expr {3.** $j} ] <= $xx1} { set pow3 $j }
if { [expr {3.** $j} ] >= $xx1} { break }
incr j 1
}
set side4 [expr {$power2+1.}]
set side5 [expr {$power3+$powerx*1.}]
set sidex [expr {sqrt($side5**2.-$side4**2.)}]
set side5 $sidex
set side6 [expr {$power3+$powerx*1.}]
return $power2 ;}
proc triplet { xx1 } {
global side4 side5 side6
set nn [ expr { int($xx1) } ]
set tt [ expr {(int ((3.+sqrt(8.*$nn-7.))/2.))*1. }]
set ss [ expr { $nn-($tt**2-3.*$tt+2.)/2 } ]
set side5 [ expr {2.*$ss*$tt } ]
set side4 [ expr {$tt**2-$ss**2 } ]
set side6 [ expr {$tt**2+$ss**2 } ]
}
proc calculate { } {
global answer2
global side1 side2 side3 side4 side5 side6
set answer2 [ triplet $side1 ]
set pi5 [pi]
if {$answer2 >= $pi5} { set error5 [expr {100.*$answer2/$pi5-100.}] }
if {$answer2 <= $pi5} { set error5 [expr {100.*$pi5/$answer2-100.}] }
#$x insert 1.0 " % error $error5 "
#$t insert 1.0 " % error $error5 "
}
proc fillup {aa bb cc dd ee ff } {
.frame.entry1 insert 0 "$aa"
.frame.entry2 insert 0 "$bb"
.frame.entry3 insert 0 "$cc"
.frame.entry4 insert 0 "$dd"
.frame.entry5 insert 0 "$ee"
.frame.entry6 insert 0 "$ff "
}
proc clearx {} {
foreach i {1 2 3 4 5 6 } {
.frame.entry$i delete 0 end
}
}
proc pi {} {expr acos(-1)}
proc inrad {a b c} {return [expr {(sqrt(($a+$b+$c)*($a+$b-$c)*($a-$b+$c)*($b+$c-$a)))/(2.*($a+$b+$c)) } ] }
proc pol { xx1 yy1 xx3 yy3 xx2 } {
return [expr { ((($xx2-$xx1)*($yy3-$yy1))/($xx3-$xx1))+ $yy1 } ] ;}
proc cir { aa bb cc } {
set radius [inrad $aa $bb $cc ]
set cirdiameter [ expr { 2.* $radius }]
set circlearea [ expr { [pi]*($radius**2) }]
set circlecircum [ expr {2.*[pi]*$radius }]
set spherevol [ expr { (4./3.)*[pi]*($radius**3) }]
set spheresurface [ expr { 4.*[pi]*($radius**3) }]
puts "$aa side 1 "
puts "$bb side 2 "
puts "$cc side 3 "
puts "$radius radius on inscribed circle"
puts "$cirdiameter if available, diameter of circle"
puts "$circlecircum if a., circumference of circle"
puts "$circlearea if a., area of circle"
puts "$spherevol if a., volume of sphere"
puts "$spheresurface if a., surface area of sphere"
}
proc reportx {} {
console show;
puts "
& The interpolation function takes
two know points on a line and
solves for an intermediate point.
The points are xx1,yy1,xx2,yy2 and xx3,?yy3?
The interpolation function loaded as
proc pol. User should be able
to cut and paste (c&p)
pol 50. 1000. 200. 1200. 150.
and save answer (1133.3) on console.
& The inrad function take the three
sides of a Babylonian triplet
and returns the radius of the
inscribed circle.
The form is inrad aa bb cc.
eg. inrad 3 4 5
& The cir function take the three
sides of a Babylonian triplet
and returns various parameters of the
triplet and inscribed circle.
The form is cir aa bb cc.
eg. cir 3 4 5
"
}
frame .buttons -bg aquamarine4
::ttk::button .calculator -text "Solve" -command { calculate }
::ttk::button .test2 -text "Testcase1" -command { clearx;fillup 1. 4. 5. 3. 4. 5. }
::ttk::button .test3 -text "Testcase2" -command { clearx;fillup 3. 12. 13. 5. 12. 13. }
::ttk::button .test4 -text "Testcase3" -command { clearx;fillup 6. 24. 25. 7. 24. 25. }
::ttk::button .clearallx -text clear -command {clearx }
::ttk::button .about -text about -command about
::ttk::button .report1 -text report -command { reportx }
::ttk::button .exit -text exit -command {exit}
pack .calculator -in .buttons -side top -padx 10 -pady 5
pack .clearallx .about .report1 .exit .test4 .test3 .test2 -side bottom -in .buttons
grid .frame .buttons -sticky ns -pady {0 10}
. configure -background aquamarine4 -highlightcolor brown -relief raised -border 30
wm title . "Searching for Bablylonian Triplets"Subroutine Math Template 4, Console Wrapper for list of normalized_set
;# pretty print from autoindent and ased editor
;# normalized_set for math::stats? package
;# working under TCL version 8.6
;# console program written on Windows 10 on TCL
;# gold on TCL Club, 26Jun2021
package require Tk
console show
package require math::numtheory
namespace path {::tcl::mathop ::tcl::mathfunc math::numtheory }
set tcl_precision 17
;# adapted from tcl-wiki Stats 2011-05-22, arithmetic mean [RLE]
;#
;# ::math::normalized_set --
;#
;# Return the list of normalized_set by division of selected quantity
;# Arguments:
;# val first value is selected quantity
;# args other values are numbers to be normalized
;#
;# Exemption 1, if input list has 1 or zero entries, return 0
;# >> args of one element, meaning no quanities, return 0
;# Exemption 2, if selected quantity has zero entries, return 0
;# >> remove possibility of division by zero
;# Results: set of normalized numbers divided by selected quantity
;#
;# $sum_? reserved for sums and averages of quantites, not used now
;#
proc ::math::normalized_set {quantity args} {
set N [ expr { [ llength $args ] + 1 } ]
if { $N == 1 } { return 0 }
if { $N == 0 } { return 0 }
if { $quantity == 0 } { return 0 }
set quantity [ expr { $quantity * 1. } ]
set sum_entries 0.
set sum_normalized 0.
foreach val $args {
set sum_entries [ expr { $sum_entries + $val } ]
set sum_normalized [ expr { $sum_normalized + $val/$quantity } ]
}
set mean [ expr { $sum_entries * 0.5 } ]
set average_normalized [ expr { $sum_normalized * 0.5 } ]
;# remove comment for sum and mean reports in printout
;# puts " sum_entries $sum_entries entries mean $mean sum_normalized $sum_normalized normalized mean $average_normalized"
foreach val $args {
lappend answer [ expr { $val * (1./$quantity) } ]
}
return $answer
}
;# check with printout >>> puts "check with printout $quantity $args answer $answer"
;# end of working deck
;# add cosmetics below to bottom of file
console show
console eval {.console config -bg palegreen}
console eval {.console config -font {fixed 20 bold}}
console eval {wm geometry . 40x20}
console eval {wm title . " Console wrapper for normalized_set proc"}
console eval {. configure -background orange -highlightcolor brown -relief raised -border 30}
puts " Console wrapper for normalized_set proc"
puts " ************************** "
puts " Begin test suite "
puts " ************************** "
puts " Return the quantities from list of normalized_set by division of selected quantity"
puts " [ ::math::normalized_set 2 2 2 2 ] "
puts " for ::math::normalized_set 2 2 2 2 returns 1.0 1.0 1.0 "
puts " for ::math::normalized_set 2 1 2 4 returns [ ::math::normalized_set 2 1 2 4 ] "
puts " for ::math::normalized_set 2 1 2 4 returns 0.5 2.0 2.0 "
puts " for ::math::normalized_set 2 1 2 3 4 5 6 7 8 9 10 returns [ ::math::normalized_set 2 1 2 3 4 5 6 7 8 9 10 ]"
puts " for ::math::normalized_set 10. 1 2 3 4 5 6 7 8 9 10 returns [ ::math::normalized_set 2 1 2 3 4 5 6 7 8 9 10 ]"
puts " [ ::math::normalized_set 2 ] << for args set of 1 element ::math::normalized_set 2 returns zero "
puts " [ ::math::normalized_set 0 ] << for ::math::normalized_set 0 returns zero "
;# end of deck Test Suite printout for list of normalized_set
Console wrapper for normalized_set proc ************************** Begin test suite ************************** Return the quantities from list of normalized_set by division of selected quantity sum_entries 6.0 entries mean 3.0 sum_normalized 3.0 normalized mean 1.5 1.0 1.0 1.0 for ::math::normalized_set 2 2 2 2 returns 1.0 1.0 1.0 sum_entries 7.0 entries mean 3.5 sum_normalized 3.5 normalized mean 1.75 for ::math::normalized_set 2 1 2 4 returns 0.5 1.0 2.0 for ::math::normalized_set 2 1 2 4 returns 0.5 2.0 2.0 sum_entries 55.0 entries mean 27.5 sum_normalized 27.5 normalized mean 13.75 for ::math::normalized_set 2 1 2 3 4 5 6 7 8 9 10 returns 0.5 1.0 1.5 2.0 2.5 3.0 3.5 4.0 4.5 5.0 sum_entries 55.0 entries mean 27.5 sum_normalized 27.5 normalized mean 13.75 for ::math::normalized_set 10. 1 2 3 4 5 6 7 8 9 10 returns 0.5 1.0 1.5 2.0 2.5 3.0 3.5 4.0 4.5 5.0 0 << for args set of 1 element ::math::normalized_set 2 returns zero 0 << for ::math::normalized_set 0 returns zero (System32) 1 %
Notes on gradient calculations.
depth=y=1 cubit, length=x=1/2, slope=tangent = y/x, B. counter-slope = cotangent = x/y. the long side y would be 1,cubit, the the short side would be variable X. B. convention was depth down as positive. < 1/2, 1/3. 1/4, 1/5, 1/6, 1/7, 1/8, 1/9, 1/10> angle would be cotan x/y
< 1/2, 1/3. 1/4, 1/5, 1/6, 1/7, 1/8, 1/9, 1/10>
slope=tangent = < 1/1/2, 1/1/3, 1/1/4, 1/1/5, 1/1/6,1/ 1/7,1/ 1/8, 1/1/9, 1/1/10>
cotangent = < 1/2/1, 1/3/1, 1/4/1, 1/5/1, 1/6/1, 1/7/1, 1/8/1, 1/9, 1/10/1>
expr 1./2./1.0 = .5 decimal = 30/60 base_60, expr 1./3./1.0.= .33333 =20/60, expr 1./4./1.0=.25 decimal, 15/60 base_60, expr 1./5./1.0= .2 decimal, 12/60 base_60. expr 1./6./1.= 0.166666 decimal, 10/60 base_60,expr 1./7./1. =0.142857 decimal, 8.571/60 base_60, expr 1./8./1= .0.125, 7.5/60 or 7/60+30/3600. base_60, expr 1./9./1.= 0.111111, 6.666/60 base_60, expr 1./10./1.=0.1, 0.6/60 or 36/3600 base_60
gold10/25/2020. Changes, removed carriage returns on many paragraphs. Added Angle table. Added paragraph on Babylonian reciprocal relationship.
Changes Log Section
Please place any changes here, Thanks.
What is your purpose in binding the motion event on your main window to execute the wm title command. I.e., this line:
bind . <Motion> {wm title . "Searching for Bablylonian Triplets"}The result of that binding is that every time you move the mouse, the "wm title" subcommand is called repeatedly. To set the window title, you just need to call "wm title . title" once, not on every event update upon mouse pointer motion.
gold changed to bare "wm title . title"
gold10/25/2020. Changes, removed carriage returns on many paragraphs. Added Angle table. Added paragraph on Babylonian reciprocal relationship.
Hidden Comments Section
Solved on 7/01/2021. Quadratic equations using TCLLIB
gold 6/29/2021. I am working on wiki page {https://wiki.tcl-lang.org/page/Seaching+for+Babylonian+Triplets+Slot+Calculator+Example ]. Can someone point me to a quadratic solution command or proc in TCLLIB? or TCL core. Understand, I have access to Quadratic solution procs in TCL or could write one. But I am looking at the files in TCLLIB math and don't recognize the quadratic solution proc section. Thank you.
AM There is none, if you mean to solve a second-degree equation. The references to "quadratic" in the math module are all for very different entities.
gold 7/2/2012. I'll write a small proc to solve quadratic equations and put a ticket in the TCLLIB que. There was an interesting note on the quadratic equation in [L3 ] & [L4 ] Thank you.
Please include your wiki MONIKER and date in your comment with the same courtesy that I will give you. Thanks, gold 12Sep2020
gold10/23/2020. code scrap under test.
Hidden Draft on Validation
;# prints gosh
;# $result returns " 1 2 3 4 5 6 7 8 9"Subject. Old Babylonian Coefficients for Triangles. Can you help me find the O.B. tablets or paper that discussed the Old Babylonian Coefficients for the Triangles? See the numbers in the attachment and internet page on the TCL WIKI. The TCL WIKI is the working group or club of the Tool Control Language TCL for programming graphical user interfaces gui. There were two similar tablets about ten years ago, but I can not find them or the translation paper anymore on the internet. The paper showed the main O.B.tablet with about 16 readable entries, purportedly on triangle coefficients. I am trying to support the theories of Mansfield & Wildberger.on the Plimpton 322 triplets. The ORACC math search engine for math tablets is returning an error on my machine. MCT and other tablets have been put behind firewalls and paywalls, such that I doubt a regular search engine could pull these content, as formerly. I have Robson's paper(s) on Old Babylonian Coefficients. Thank you, xxx
[L5 ] [L6 ] Other tablets supporting the use of Plimpton 322 triplets.
References:
References: •Importing expr functions, part 2 •http://www.grahamhancock.com/forum/KollerstromN4.php? •The Lost Science of Measuring the Earth:Robin Heath, John Michell •http://en.wikipedia.org/wiki/Japanese_units_of_measurementMean •Thureau Dagin, RA28 •Chaldean uses in 1915 text by Neugebauer and Weidner •http://oracc.museum.upenn.edu/cdli/corpus •http://cdli.ucla.edu/pubs/cdlj/2005/cdlj2005_002.html •http://cojs.org/cojswiki/Mathematical_Tablet_from_Ebla,_c.2350-2250_BCE •http://www.helsinki.fi/~whiting/math.html •Eleanor Robson, Mesopotamian Mathematics, 2100-1600 BC (Oxford, 1999) •http://www.math.tamu.edu/~dallen/masters/egypt_babylon/babylon.pdf •http://www.mathdb.org/articles/history_pi/e_history_pi.htm •http://en.wikipedia.org/wiki/Japanese_units_of_measurement •http://oeis.org/search?q=+A060355+&language=english&go=Search •http://www.mathsisfun.com/numbers/prime-factorization-tool.html •Oneliner's Pie in the Sky •Tip in a search engine, type "cdli 30" ,"cdli sag","cdli 20",or "cdli05" •30, 20, and 05 are searches for sexagesimal notation.
storage.
Question? Are all the tablets that interest you cited in Robson, Eleanor?" Answer No. I am a retired computer programmer and essentially looking for fresh content on , more than what is referenced in my internet article. Its been 6 years since the Mansfield and Wildberger study was published on internet, see attachment.. So presumably there might? be fresh information within academic circles on Old Babylonian coefficient lists. A keyword search on " Eleanor Robson Old Babylonian coefficient lists" or "Eleanor Robson Old Babylonian coefficient lists" brings up ORACC note by Robson, Eleanor. on 15 July 2010. The keywords in the referenced internet searches are the most successful to date. Eleanor Robson in UK was a major researcher in this narrow field of Old Babylonian coefficient lists, and I am particularly interested in the Robson updated items at the ORACC, Upenn. The CDLI at UCLA is another large "dump" of searchable tablet images and content and interconnected with Yale and British Museum ( I think?). https://cdli.ucla.edu Like I said, I am a retired engineer and computer programmer and mostly dependent on the professional mathematicians and Old Babylonian translators (published monographs, I mean). The internet is continually shifting and I guess I will have to learn some search tricks. Thank you, again.
| Category Numerical Analysis | Category Toys | Category Calculator | Category Mathematics | Category Example | Toys and Games | Category Games | Category Application | Category GUI |