Version 118 of Math proc templates for Prime Number generation and TCL demo example, numerical analysis
Updated 2021-05-27 17:58:13 by goldMath proc templates for Prime Number generation and TCL demo example, numerical analysis
This page is under development. Comments are welcome, but please load any comments in the comments section at the bottom of the page. Please include your wiki MONIKER and date in your comment with the same courtesy that I will give you. Aside from your courtesy, your wiki MONIKER and date as a signature and minimal good faith of any internet post are the rules of this TCL-WIKI. Its very hard to reply reasonably without some background of the correspondent on his WIKI bio page. Thanks,gold 30Apr2021
- Math proc templates for Prime Number generation and TCL demo example, numerical analysis
- Introduction
- prime number formula < 16n+15 >
- primes on clay tablets
- Importance of Explicit Instructions for Market Rates on Tablet IM31210P4
- Mathematical functions that somewhat track with the Prime Counting Function PCF(X)
- Table 4. Reconstructed listing of Babylonian Base_60 inverse reciprocals
- Table 5. Reconstructed listing of the triplets on Tablet Plimpton 322
- Subroutine Template 1, division of quantity by two or more given ratios
- Subroutine Template 2, sqrt_sum_of_squares
- output for sqrt_sum_of_squares
- Subroutine Template 3, quantity_into_multiple_ratios
- printout for quantity_into_ratios proc
- Pseudocode, Equations, and Wiki Page Checklist
- Subroutine Template 4, geometric_mean
- Pseudocode on primes in Babylonian triplets
- Possible Errors, Predefined Entries, Break Lines, Possible Wild_Cards in TCLLIB::math local copy
- Testcases Section
- Screenshots Section
- Screenshots Section
- figure 1a. Console wrapper for prime_formula proc
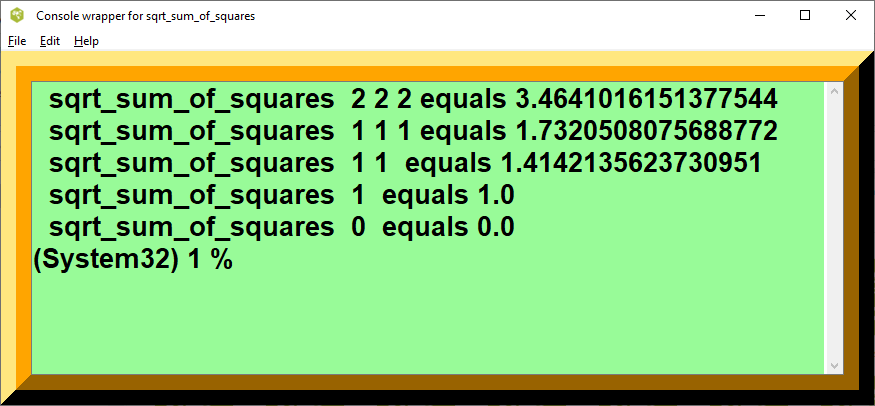
- figure 1b, Console wrapper for sqrt_sum_of_squares
- figure 1c, Console wrapper for sqrt_sum_of_squares
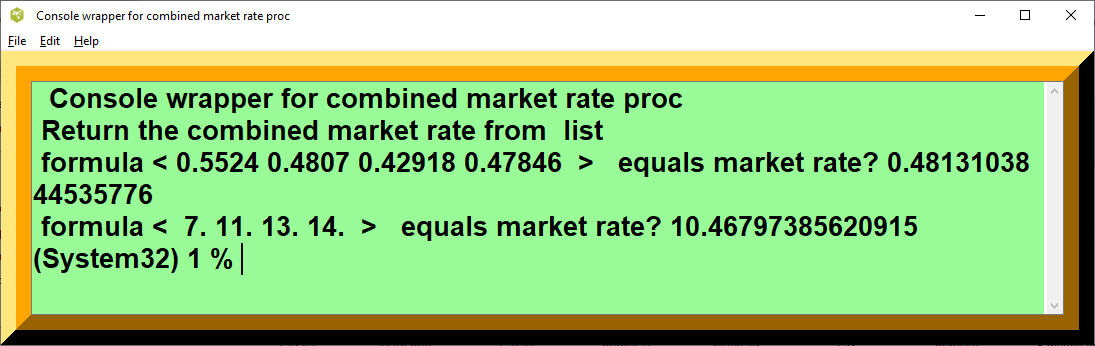
- figure 1d, Market_Rate_Problem
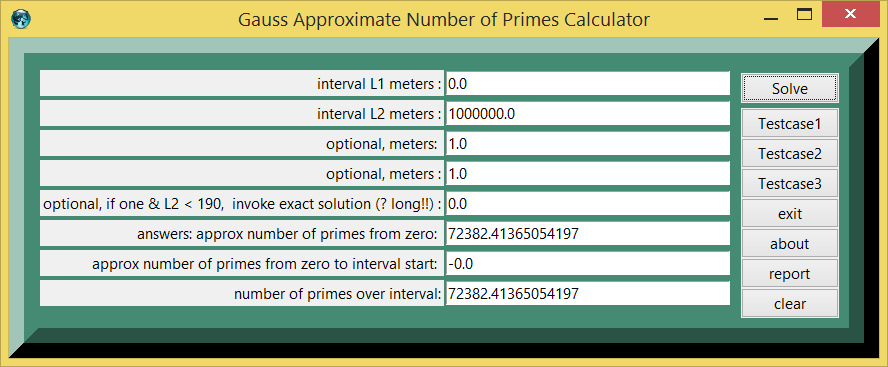
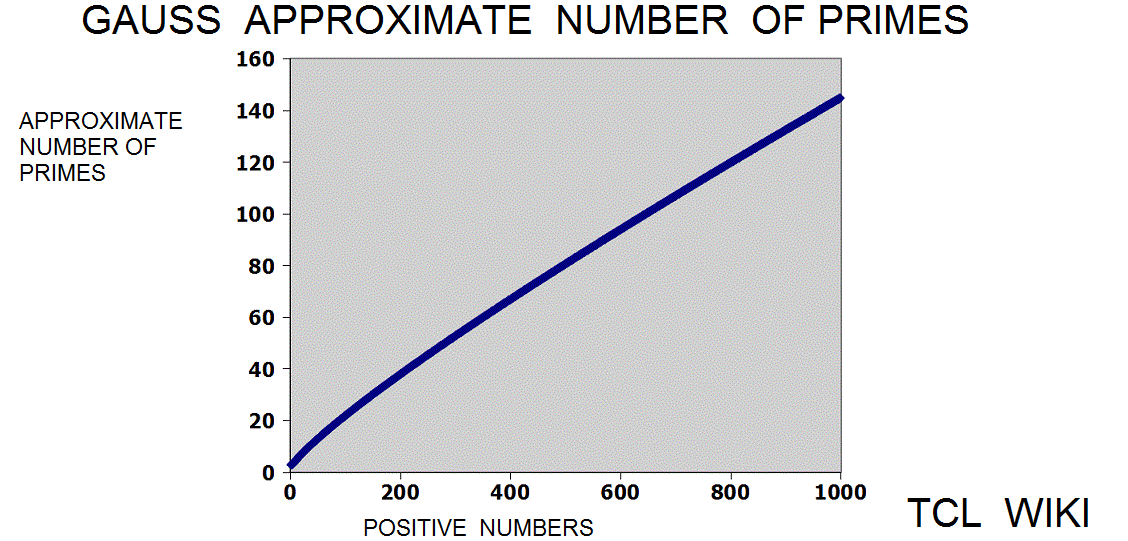
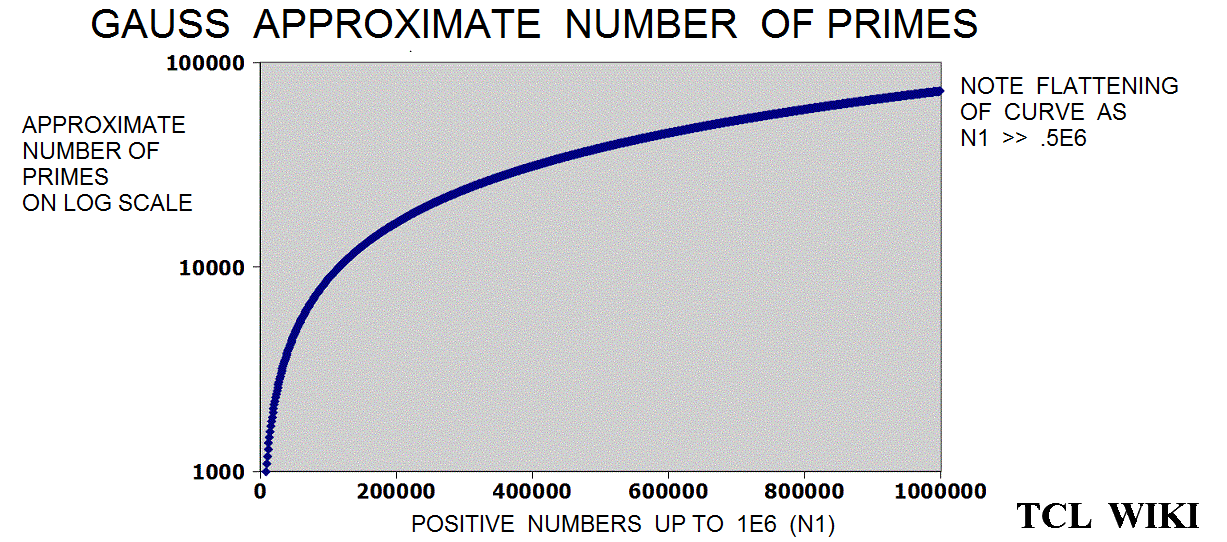
- figure 1e, Gauss Approximate Number of Primes
- figure 2.
- figure 3.
- figure 4.
- figure 5.
- figure 6.
- figure 7.
- figure 8.
- figure 9.
- figure 10.
- figure 11.
- figure 12.
- References:
- References:
- Appendix Code
- Hidden Comments Section
Introduction
gold Here are some Math proc templates for Prime Number generation. These Math proc templates are intended to be compatible with the format of existing subroutines in the TCLLIB:math library. The new Math proc should be checked in TCLLIB::math local copy before submission to TCLLIB ticket pipeline. Morfing these math proc templates into Prime Number generation subroutines should be feasible. I have found it easier and more tidy to start with a working TCL templates and morf a few lines into a new purpose.If one completes and tests the new TCL subroutine in a console program, then usually one can load the new TCL subroutine into a graphical user interface (gui).
prime number formula < 16n+15 >
Maybe coincidence, but sequence {7 11 13 14 } has been found on Sumerian Tablet AO8862. The On-Line Encyclopedia of Integer Sequences A014311 Oeis {7 11 13 14} cited sequence property as Numbers n such that <16n+15> are prime. Tablet YBC10722 uses the input quantity 15 with the sequence {7 11 13 14}! KWJ in Monster Prime Predicting Formula has posted on the Wiki for this formula < 16n+15 >.
This prime number formula < 16n+15 > as a prime number filtering mechanism produces some primes and some duds. KWJ reported the prime number formula < 16n+15 > had an efficiency of 0.166 for filtering primes out of the numberline,for the data set, <PLT500K>. For N > 2, about half of numbers on the numberline are even, which could never be defined as primes. If the formula added two even numbers, then only even numbers would result in the sum with no primes produced. If the formula added an even number and odd number, then some odd numbers might result with some primes produced.
primes on clay tablets
In some sense, the Plimpton 322 clay tablet is also generating a set of prime numbers in the available triplet collection on the clay tablet. The Babylonian regular numbers in base_60 between 0 and 60 have a limited set of triplets that satisfy 1< X-1/X < 1+sqrt(2) which appears to be the role of Plimpton 322. The limit 1< X-1/X < 1+sqrt(2) may explain the 1<X<2 limit on the Late Babylonian many place reciprocal tablets.
While the modern mathematicians are trying to find prime numbers in base_10, the Babylonian mathematicians in base_60 were trying to avoid prime numbers. The primes are the Achilles heel of the Babylonian multiplication system using reciprocals in base_60. The number set in the sequence {7 11 13 14} was especially foul to the Babylonian multiplication system, although the Babylonian mathematicians did use the set {7 11 13 14} in arithmetic or "advanced non-standard" calculations. One trick that the Babylonian mathematicians was to multiply an odd number or prime number by 2 or 3 at one early stage of the calculations and then divide out respectfully the 2 or 3 at a later stage of the calculations. For example, 7*2 converts an overtly prime number to a number 14 with factors 2*7. However, this multiplication trick with 2 or 3 as factors is confusing in the extant school and library tablets, so sometimes the modern reader is stressed by a missing factor of 2/3 after corrupted or dropped tablet lines.
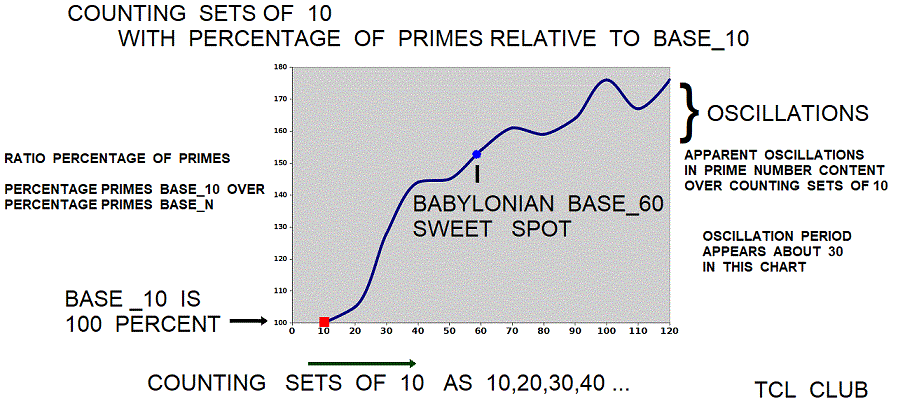
| table 1 Percentage Primes in Modern Base_10 and Babylonian Base_60 | printed in | tcl wiki format | |
|---|---|---|---|
| quantity | value | value | comment, if any |
| set_number: | percent of prime numbers in set | percent primes in set of 10 over / set of N | |
| set 10 : | 44.44 | 1.0 | Modern base_10 |
| set 20 : | 42.10 | 1.05 | Archaic IndoEuropean base_20 |
| set 30 : | 34.48 | 1.28 | |
| set 40 : | 30.76 | 1.44 | |
| set 50 : | 30.61 | 1.45 | |
| set 60 : | 28.81 | 1.54 | Babylonian base_60 |
| set 70 : | 27.53 | 1.61 | |
| set 80 : | 27.84 | 1.59 | |
| set 90 : | 26.96 | 1.64 | |
| set 100 : | 25.25 | 1.76 | |
| set 110 : | 26.60 | 1.67 | |
| set 120 : | 25.21 | 1.76 |
;# using TCLLIB math prime subroutines
;# COUNTING SETS OF 10 WITH PERCENTAGE OF PRIMES RELATIVE TO BASE_10
puts "%| set_number:|percent of prime numbers in set | |%"
foreach value {10 20 30 40 50 60 70 80 90 100 110 120} {
puts "&| set $value :|[ expr { [llength [ primesLowerThan [- $value 1 ] ]]*100./ [- $value 1 ] }] |[ expr { ([llength [ primesLowerThan [- 10 1 ] ]]*100./ [- 10 1 ] )/( [llength [ primesLowerThan [- $value 1 ] ]]*100./ [- $value 1 ]) }] | |&" }Here in this article, the combined market rate is defined as the combination of two or more market rates, effectively the reciprocal of the average price. Some of the problems seem directed towards calculating a combined market rate or combined value for a market basket of goods or stock on hand. Very interesting in terms of the history of economics and capitol gains, as the problems suggest Babylonian interest in the overall health of the marketplace or overall value of stocks in hand. The Babylonian Astronomy Diaries record some prices of the marketplace economy and suggest these combined market rate problems were a special interest of the Babylonian Astronomy Group Mathematicians. These Babylonian Astronomy Group Mathematicians were the most advanced mathematicians in Babylon, so any insight into their mind set should be useful in historical terms.
Use the set {7 11 13 14} which contains primes for the market rate problem, but also include the Babylonian algorithm of summing Base_60 reciprocals in the midstage or followup calculations. The correct calculation of the sum of the base_60 reciprocals is the key to the market rate problem. Most school tablets have the sum of the base_60 reciprocals posted in the top margin as well as listed in a column and rows. The sum of the base_60 reciprocals is <expr 8.5714 + 5.4545 + 4.6153 + 4.2857 > as 22.9/60. The sum of the base_60 reciprocals is the sum of the prices for every type in the basket and the total price for each kind (type) is 22.9/60. Here the sum of shares is set to 60 pieces. Share a is <expr 8.5714*(60./22.9 )> or 22.4578 ; share b is <expr 5.4545*(60./22.9 )> or 14.2912 ; share c is <expr 4.6153*(60./22.9)> or 12.09248 ; share d is <expr 4.2857 *(60./22.9)> or 11.2289 , using decimal notation here.
| table 2 Using primes in Market Rate Problem | Babylonian algorithm of summing base_60 reciprocals | printed in | tcl wiki format | |
|---|---|---|---|---|
| quantity | market rate ( value) | market price ( 60 / value ) | 1.0 / value | comment, if any |
| conventional id | tablet value | base_60 reciprocal | base_10 reciprocal | TCL expression |
| market rate 1 | 7 | 8.5714 | 0.14285 | expr { 60. / 7} |
| market rate 2 | 11 | 5.4545 | 0.09090 | expr { 60. / 11} |
| market rate 3 | 13 | 4.6153 | 0.07692 | expr { 60. / 13} |
| market rate 4 | 14 | 4.2857 | 0.071428 | expr { 60. / 14} |
| sum base_60 reciprocals | 22.9269 | sum base_60 = expr {8.5714 + 5.4545 + 4.6153 + 4.2857 } | ||
| sum base_10 reciprocals | 0.382098 | sum base_10 = expr {0.14285 + 0.09090 + 0.07692+ 0.071428 } | ||
| *** | midstage or follow up calculations for | Babylonian algorithm of summing base_60 reciprocals | *** | |
| *** | midstage or follow up calculations | beware, some tablets have an algorithm fork here | *** | |
| *** | >>if<< sum base_60 reciprocals greater than 60 pieces | *** | ||
| share a | 22.4578 | expr 8.5714*(60./22.9 ) | ||
| share b | 14.2912 | expr 5.4545*(60./22.9 ) | ||
| share c | 12.09248 | expr 4.6153*(60./22.9) | ||
| share d | 11.2289 | expr 4.2857 *(60./22.9) | ||
| *** | final stage or follow up calculations for | Babylonian algorithm of summing base_60 reciprocals | *** | |
| *** | this was the proof that calculations were done correctly, | but not included on some tablets. | *** | |
| estimated total shares < a+b+c+d> | 60.07038 | total shares = expr { 22.4578 +14.2912 + 12.09248 + 11.2289 } | ||
| average share per entry for < a+b+c+d> | 15.0 | average share per entry = expr {60. /4}, maybe where 15 comes from on tablet? |
For a check on the TCL calculator algorithm, a combined work norm was calculated in several ways using hand calculations, TCL template routines, and the Babylonian algorithm of summing Base_60 reciprocals. A combined work norm was calculated using 3 work norms < 20,10,6+40./60> volume shekels per day with the given answer as 10 volume shekels per day. The combined work norm can be calculated alternately from the combined market rate methods and include the Babylonian algorithm of summing Base_60 reciprocals. The hand calculation was expr 3/(1/20.+1/10.+1/(6+40./60)) = 10 (ref. modern definition of harmonic means). The TCL template routine for combined market rate returns < ::math::combined_market_rate 20. 10. 6.666 > equals market rate? 10.0 rounded.
| table 3 | combined work norm | printed in | tcl wiki format | |
|---|---|---|---|---|
| quantity | market rate ( value) | market price ( 60 / value ) | 1 / value | comment, if any |
| conventional id | tablet value | base_60 reciprocal | base_1 0 reciprocal | |
| work rate norm 1 | 20 | 3.0 | 0.05 | norm 1 = expr {60./20} |
| work rate norm 2 | 10 | 6.0 | 0.1 | norm 2 = expr {60./10} |
| work rate norm 3 | 6.666 | 9.0 | 0.15 | norm 3 = expr {60./6.666} |
| sum base_60 reciprocals | 18. | sum = expr { 3+6+9.} | ||
| sum base_10 reciprocals | 0.30 | sum = expr { 0.05+0.1+ 0.15 } | ||
| *** | midstage or follow up calculations for | Babylonian algorithm of summing base_60 reciprocals | *** | |
| *** | midstage or follow up calculations | beware, some tablets have an algorithm fork here | *** | |
| share a | 10. | share a = expr { 3.0 * (60./18. ) } | ||
| share b | 20. | share b = expr { 6.0 * (60./18. ) } | ||
| share c | 30. | share c =expr { 9.0 *(60./18. ) } | ||
| estimated total shares < a+b+c> | 60. | total shares = expr { 10 + 20 + 30 } | ||
| average share per entry for < a+b+c> | 20. | average share = expr { ( 10 + 20 + 30 ) / 3. } |
puts "%|table 6 |printed in| tcl wiki format|% "
puts "&| quantity| 60 / value| 1/ value|comment, if any|& "
puts "&| entry |percent of prime numbers in set | |&"
foreach value {1.81 2.08 2.33 2.09 } {
puts "&| $value | [/ 60. $value ] |[/ 1. $value ] | |&" }
foreach value {7 11 13 14 } {
puts "&| $value | [/ 60. $value ] | [/ 1. $value ] | |&" } Joran Firberg provided some commentary on 2 market rate problems on tablet, MS28302a and MS28302b, ref Friberg, A Remarkable Collection of Babylonian Mathematical Texts. The preparation for the MS28302a problem was evaluation of { 1.0 + 30/60. +20./60 + 15/60. }, reduction to { 1.0 + 1.+ 5/60. }, and sum = 2+5/60. The solution was base_60 reciprocal as expr 60. /(2+(5./60)) >> 28.7999 or 28+48/60. The problem 2a shows some of the quirks of the Base_60 system in that Babylonian mathematicians jumped around 1=60=1, the reciprocal inverse of 1 was expr {1/1.} or 1, and did not use zero’s. The first inverse in the problem 2a was (1/1.) while other three inverses could be handled expr { 60. / N }. The solution for the MS 2830 § 2b problem was expr 60/64.*60. = 56.25 or 56+15/60. Its clear that the TCL market rate template probably could use some exception handling for one’s, zero’s, and null’s.
| Table 4 for problem MS28302a | printed in | tcl wiki format | ||
|---|---|---|---|---|
| quantity | market rate ( value) | market price ( 60 / value ) | comment, if any | |
| conventional id | tablet value | base_60 reciprocal | ||
| market rate 1 | 1 | 1.0 | 28+48/60. | 28+48/60. |
| market rate 2 | 2 | 30.0 | 14 +24/60. | 28+48/60. |
| market rate 3 | 3 | 20.0 | 9+36/60. | 28+48/60. |
| market rate 4 | 4 | 15.0 | 7+12/60. | 28+48/60. |
| sum | 2+5/6 | { 1.0 + 30/60. +20./60 + 15/60. }= { 1.0 + 1.+ 5/60. }, sum = 2+5/60 | ||
| sum | 60. | sum = expr { 28+48/60. +14 +24/60. + 9+36/60. +7+12/60.} | ||
| share a | 28+48/60. | share a = expr { 1.0 * (60./(2+5./60) ) } , 28.7999 | ||
| share b | 14 +24/60. | share b = expr { 1.0 * (60./(2+5./60) ) }, 14.39999 | ||
| share c | 9+36/60. | share c = expr { 1.0 * (60./(2+5./60) ) },9.6 | ||
| share d | 7+12/60. | share d = expr { 1.0 * (60./(2+5./60) ), 7.199999 | ||
| Note | ref Friberg commentary on tablet MS28302a, | A Remarkable Collection of Babylonian Mathematical Texts. | ||
| Note | The tablets use Base_60 fractions | But the TCL calculations throw out modern Base_10 decimals |
| Table 5 for problem MS28302b | printed in | tcl wiki format | ||
|---|---|---|---|---|
| quantity | market rate ( value) | market price ( 60 / value ) | comment, if any | |
| conventional id | tablet value | base_60 reciprocal | ||
| market rate 1 | 2. | 30.0 | 56+15/60 | |
| market rate 2 | 3. | 20.0 | 56+15/60 | |
| market rate 3 | 15. | 4.0 | 56+15/60 | |
| market rate 4 | 6. | 10.0 | 56+15/60 | |
| sum base_60 reciprocals | 64.0 | sum = expr {30.0 + 20.0+ 4.0 + 10.0 } | ||
| combined market rate solution | 56+15/60 | expr 60/64.*60. = 56.25 or 56+15/60 | ||
| share a | 28+7/60. +30/3600 | share a = expr { 30.0 * ((56+15/60.)/ 60. ) }, 28.125 | ||
| share b | 18+45/60. | share b = expr { 20.0 * ((56+15/60.)/ 60. ) }, 18.75 | ||
| share c | 3+45/60. | share c = expr { 4.0 * ((56+15/60.)/ 60. ) },3.75 | ||
| share d | 9+22/60. +30/3600. | share d = expr { 10.0 * ((56+15/60.)/ 60. ) }, 9.375 | ||
| Note | ref Friberg commentary on tablet MS28302a, | A Remarkable Collection of Babylonian Mathematical Texts. | ||
| Note | The tablets use Base_60 fractions | But the TCL calculations throw out modern Base_10 decimals |
Importance of Explicit Instructions for Market Rates on Tablet IM31210P4
Joran Firberg provided some commentary on a market rate problem on tablet IM31210P4 and included preparatory comments on more complete features of tablet MS2299, ref Friberg, A Remarkable Collection of Babylonian Mathematical Texts. Only the midstage calculations were legible on tablet IM31210P4, but important lexical ques and numbers were preserved in the midstage calculations. The preparation for the IM31210P4 problem was summing the costs, evaluation of expr { ( (30./60) + 2. + ( 1.+20./60) + (45./60.) ) } , and sum of costs = 4.5833 decimal in grain units. The solution was base_60 as adding total shares to 1_31_40 sexagesimal. Firberg gives the scale factor for the shares as 1_31_40 / 4_35 sexagesimal, 20. Decimal would be expr { (1 + 31/60. + 40./3600) /(4.+35./60) }, 0.3333 decimal translates to 1/3 or 20/60.
The setup or initial stage of the market rate problem usually gives two to seven market rates. The reciprocal of a market rate is supposed to be the Base_60 reciprocal or inverse of of the market price. There appear to be two types of midstage calculation. If the sum of the prices equals one silver shekel, or really 60 silver pennies, then the scale factor is (total price (1)) / ( sum prices ). If the sum of the prices equals more than one in total commodity, then the scale factor is calculated differently (total price (>> 1)) / sum prices ) . The solution was base_60 as either adding total shares up to 1 (60) sexagesimal or else adding total shares to more than one (>> 1) in total commodity. Usually the total shares as 1 or more were a given, sometimes noted as one silver shekel or more than one in the first headers or on the edge of the tablet. The final stage or follow up calculations for the Babylonian algorithm of summing base_60 reciprocals. This summing the shares was the proof that calculations were done correctly, but not included on some tablets.
A market rate procedure in TCL for just one unit price and available silver could be derived, which would be a simple problem, but shows the genesis of the Babylonian algorithm of summing base_60 reciprocals in using a false share. The Babylonians did not use algebra, but the explanation uses algebra for the context of developing a TCL procedure. The initial equation for one unit price would be $false_share * $unit_price = $available_silver. The $false_share equals $available_silver / $unit_price. The $false_share equals proc false_share1 { available_silver unit_price } { return < expr { $available_silver / $unit_price > }. There should be instances of either where the $available_silver equals one or where the $available_silver is greater than one. This is where the testcases come in to check the math. Now suppose that Babylonian mathematician wants to use two or multiple unit prices, say four unit prices. The initial equation for four unit prices would be $available_silver = $false_share * $unit_price_1 + $false_share * $unit_price_2 + $false_share * $unit_price_3 + $false_share * $unit_price_4. Combining the 4 unit prices and transposing, the $false_share = $available_silver / ( $unit_price_1 + $unit_price_2 + $unit_price_3 + $unit_price_4 ). Doable, but one is adding four new variables to the TCL procedure. The $false_share equals proc false_share2 { available_silver $unit_price_1 $unit_price_2 $unit_price_3 $unit_price_4 } { return < expr { $available_silver / ($unit_price_1 + $unit_price_2 + $unit_price_3 + $unit_price_4 ) > }. Now the Babylonian market did not use unit prices usually, but reported market rates only, so add an initial conversion step to transform market rates to market prices. In sexagesimal notation, a market price is the Base_60 reciprocal or inverse as expr < 60. / market_rate> and the Babylonian mathematicians used a tablet of reciprocal conversions. The Base_60 reciprocals are a little tricky that I admit, but we could put the reciprocal conversion scheme from market rates to market prices ahead of the proc false_share2. Once the value of the false share is found, the equation for programming the check answer is $available_silver = ( $false_share*$unit_price_1 + $false_share*$unit_price_2 + $false_share*$unit_price_3 + $false_share*$unit_price_4 ).
;# Babylonian algorithm of summing base_60 reciprocals
;# in using a false share
set unit_price_1 [ expr { 60. / $market_rate_1 } ]
set unit_price_2 [ expr { 60. / $market_rate_2 } ]
set unit_price_3 [ expr { 60. / $market_rate_3 } ]
set unit_price_4 [ expr { 60. / $market_rate_4 } ]
proc false_share2 { available_silver $unit_price_1 $unit_price_2 $unit_price_3 $unit_price_4 } { return [ expr { $available_silver / ($unit_price_1 + $unit_price_2 + $unit_price_3 + $unit_price_4 ) ] }| Table 10 for problem MS2299 | printed in | tcl wiki format | |||
|---|---|---|---|---|---|
| *** setup or initial stage for Babylonian algorithm of summing base_60 reciprocals *** | |||||
| given, available silver | 16_53_20 sexagesimal | ||||
| given, 4 unit costs | |||||
| *** midstage or follow up calculations, sum unit costs | |||||
| quantity | value | 60 / value | comment, if any | ||
| conventional id | reconstructed tablet value | base_60 reciprocal | |||
| market rate 1 | 3.0 | 20.0 | 5_55_33_20 | 17_46_40 | |
| market rate 2 | 4.0 | 15.0 | 4_26_40 | 17_46_40 | |
| market rate 3 | 5.0 | 12.0 | 3_33_20 | 17_46_40 | |
| market rate 4 | 6.0 | (10) | 2_57_46_40 | 17_46_40 | omitted on tablet |
| *** final stage , sum shares *** | |||||
| sum costs | 57.0 | expr {20.0+15.0+12.0 +10.0 } | cost relative numbers added correctly, but tricky in programming |
&|given, available silver | 16_53_20 sexagesimal | | | available silver = expr {(16+(53./60)+(20./3600)) }, 16.8888 decimal Base_10 |&
| scale factor | 17.7777 decimal | scale factor = expr {(16+(53./60)+(20./3600)) /(57/60.)}, 17.7777 decimal Base_10 |
&| share a | 5.9259 | | | share a = expr { (20.0/60)* (16+(53./60)+(20./3600)) /(57/60.) } 5.9259, decimal Base_10 |& &| share b | 4.444425 | | | share b = expr { (15.0/60)* 17.7777 } 4.444425 decimal Base_10 |& &| share c | 3.55554 | | | share c = expr { (12.0/60)* 17.7777 } 3.55554 decimal Base_10 |& &| share d | | | | share d = expr { (10.0/60)* 17.7777 } 2.962949 decimal Base_10 |&
| sum shares | 16.88883 | equal to given, available silver | sum shares = expr { 5.92592 + 4.444425 + 3.55554 + 2.962949 }, 16.88883 | ||
| Note | ref Friberg commentary on tablet IM31210P4, | A Remarkable Collection of Babylonian Mathematical Texts. | |||
| Note | The tablets use Base_60 fractions | But the TCL calculations throw out modern Base_10 decimals |
| Table 9 for problem IM31210P4 | printed in | tcl wiki format | ||
|---|---|---|---|---|
| quantity | market rate value | market price value (60 / value) | comment, if any | |
| conventional id | reconstructed? tablet value | base_60 reciprocal | ||
| market rate 1 | 30. | 2.0 | 4.5833 | ref B. relative value, this 2 = 2 *60 |
| market rate 2 | 2.0 | 0.5 | 4.5833 | |
| market rate 3 | 1.3333 | 0.75 | 4.5833 | |
| market rate 4 | 0.75 | 1.3333 | 4.5833 | |
| sum costs | 4.5833 | cost relative numbers added correctly, but tricky in programming | ||
| share a | 10 | share a = expr { 20. * 30/60.} = 10. | ||
| share b | 40 | share b = exp=r { 20. * 2.} = 40. | ||
| share c | 26+40/60. | share c = expr { 20. * (1+20/60.)} = 26.6666 | ||
| share d | 15 | share d = expr { 20. * 45/60.} = 15. | ||
| sum shares | 1_31_40 sexagesimal | sum shares = expr { 10+40+26+40./60+15} = 91.6666, ~ 1+31/60+40/3600 | ||
| Note | ref Friberg commentary on tablet IM31210P4, | A Remarkable Collection of Babylonian Mathematical Texts. | ||
| Note | The tablets use Base_60 fractions | But the TCL calculations throw out modern Base_10 decimals |
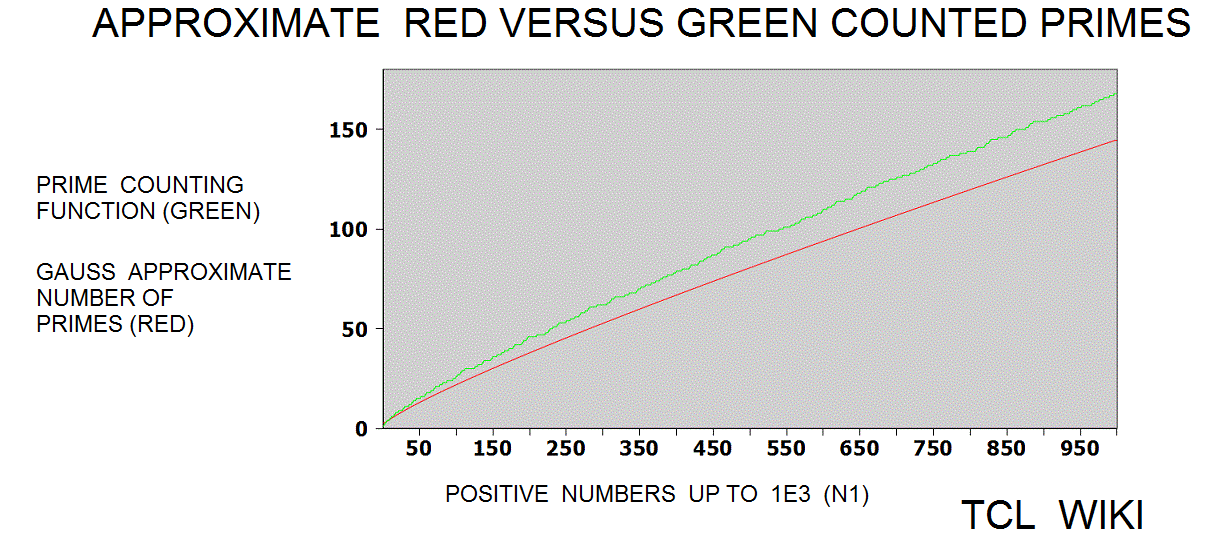
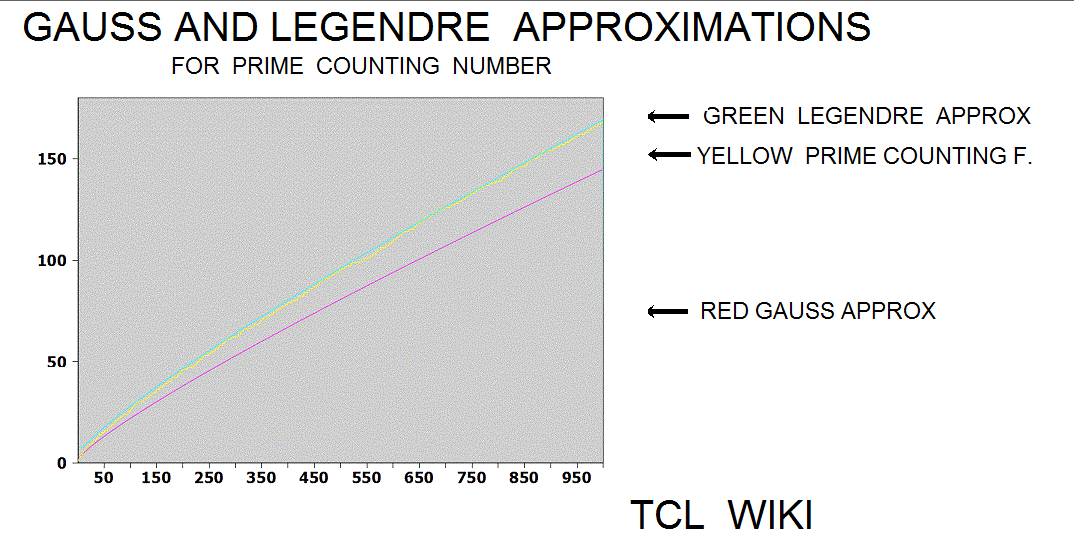
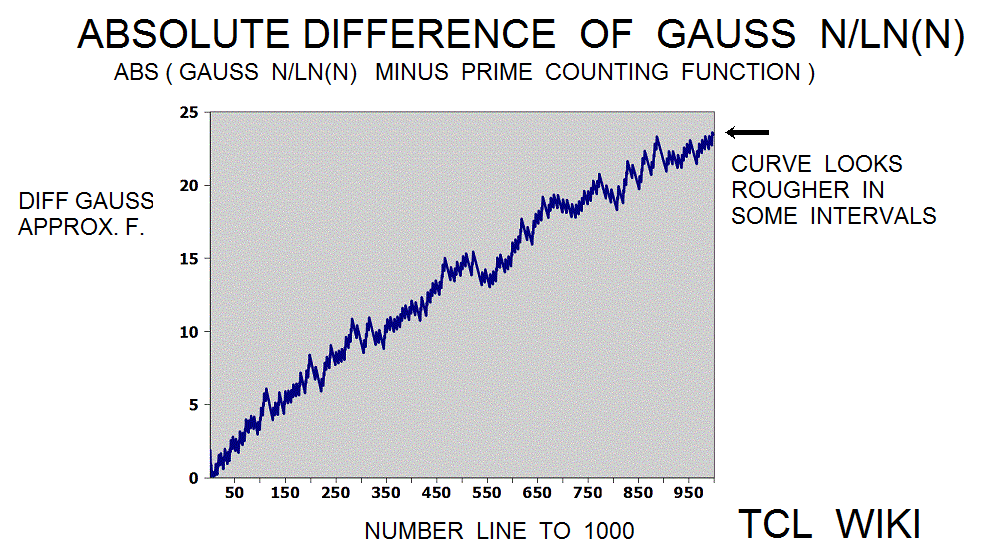
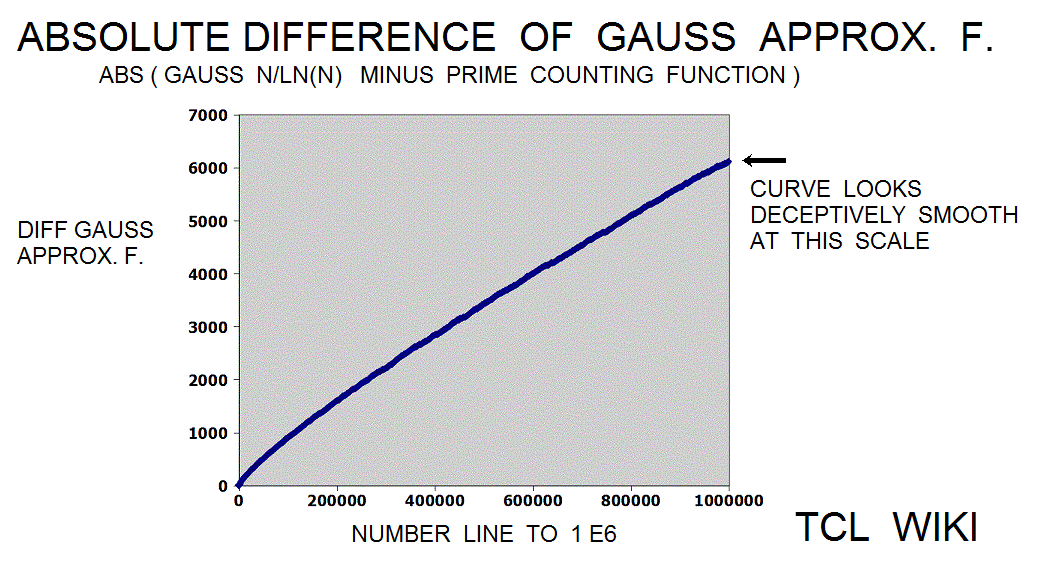
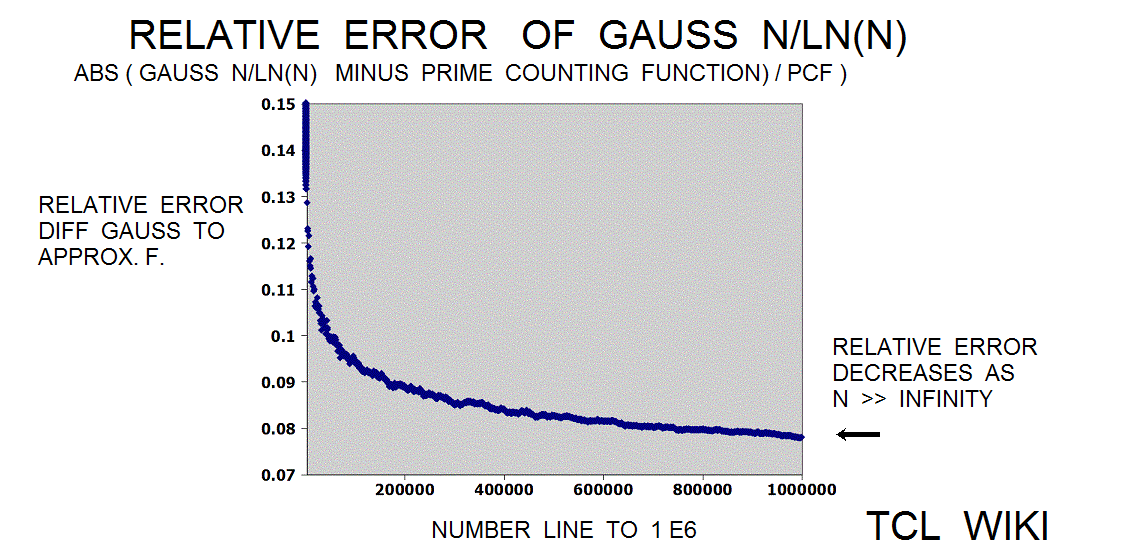
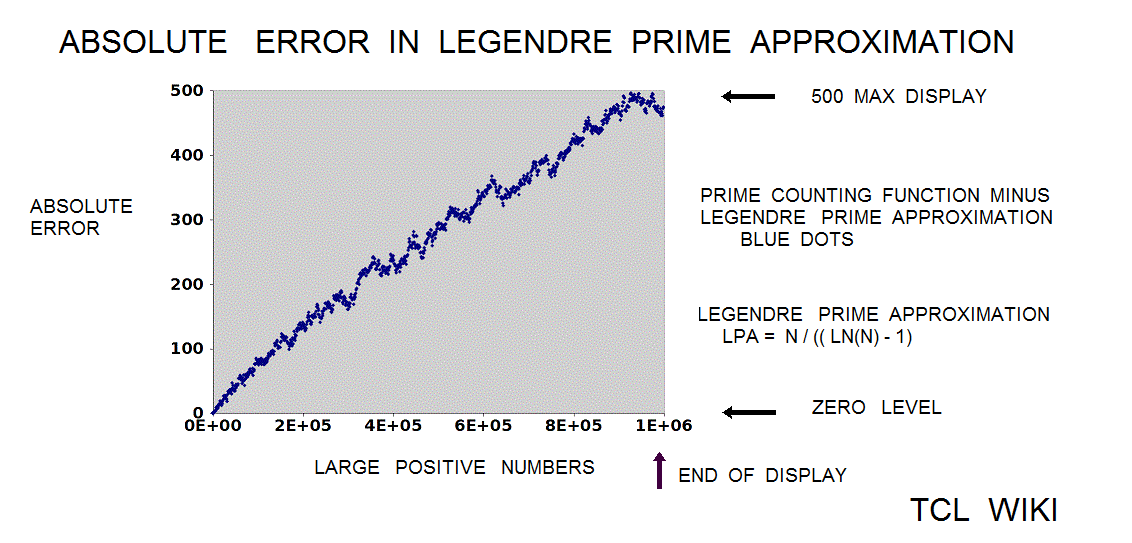
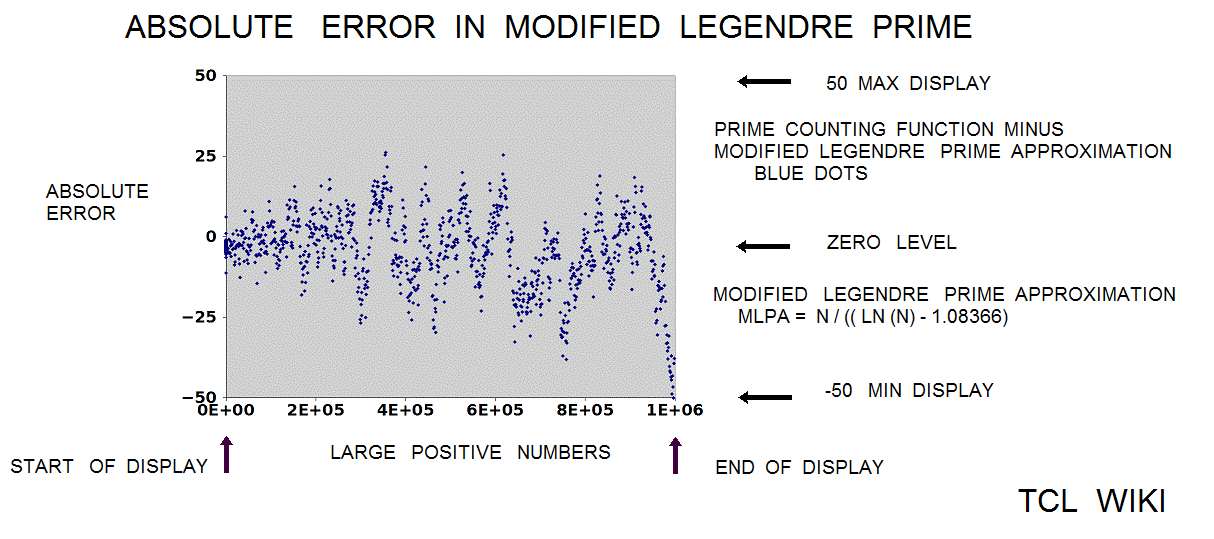
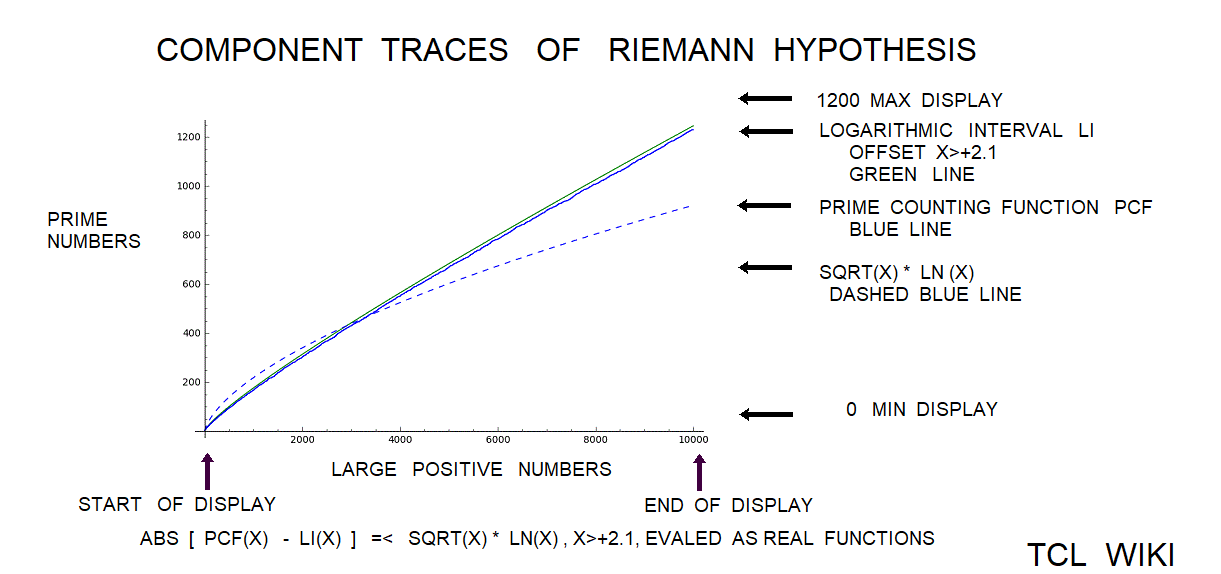
Mathematical functions that somewhat track with the Prime Counting Function PCF(X)
Other mathematical functions that somewhat track with the Prime Counting Function PCF(X) are the Logarithmic Interval Function LI(X) and the combined function Sqrt(X) * LN(X). Such that ABS {PCF (X) - LI(X) } =< Sqrt(X) * LN(X) , X>2.1, evaled as real functions. See the chart which indicates the combined function Sqrt(X) * LN(X) is a usefull upper limit for the Prime Counting Function PCF(X) in the region between 0 < PCF(X) < 4000.
c**2= a**2 + b**2
c**2= a**2 + 1 normalized Babylonian triplet
a**2 = c**2 -1 normalized Babylonian triplet
some b and c are both primes.
some b and c are not both primes.
The reciprocal pair relationship.
(X+1/X)**2 - (X+1/X)**2 = 4 , divide equation by 4
normalized triplet, < (1/4)* ((X+1/X)**2 ) , 1 ,(1/4)* ((X+1/X)**2) >
0 < X-1/X < 2
1< X-1/X < 1+sqrt(2) ~~ approximate limit of 2.4 Table 4. Reconstructed listing of Babylonian Base_60 inverse reciprocals
| Table 8 for Base_60 inverse reciprocals | printed in | tcl wiki format | ||
|---|---|---|---|---|
| Base_60 value | Base_60 inverse reciprocals or 60 / value | Base_10 value | Base_10 value of Base_60 inverse reciprocals | comment, if any |
| tablet value | base_60 reciprocal | |||
| 2 | 30 | 2 | 30 | |
| 3 | 20 | 3 | 20 | |
| 4 | 15 | 4 | 15 | |
| 5 | 12 | 5 | 12 | |
| 6 | 10 | 6 | 10 | |
| 8 | 7 30 | 8 | 7.5 | |
| 9 | 6 40 | 9 | 6.6666 | |
| 10 | 6 | 10 | 6 | |
| 12 | 5 | 12 | 5 | |
| 15 | 4 | 15 | 4 | |
| 16 | 3 45 | 16 | 3.75 | |
| 18 | 3 20 | 18 | 3.3333 | |
| 20 | 3 | 20 | 3 | |
| 24 | 2 30 | 24 | 2.5 | |
| 25 | 2 24 | 25 | 2.4 | |
| 27 | 2 13 20 | 27 | 2.2222 | |
| 30 | 2 | 30 | 2 | |
| 32 | 1 52 30 | 32 | 1.875 | |
| 36 | 1 40 | 36 | 1.6666 | |
| 40 | 1 30 | 40 | 1.5 | |
| 45 | 1 20 | 45 | 1.3333 | |
| 48 | 1 15 | 48 | 1.25 | |
| 50 | 1 12 | 50 | 1.2 | |
| 54 | 1 06 40 | 54 | 1.1111 | |
| 1 | 1 | 1 | 1 | exception handling alert 1=1 NE ( 60/value ) |
| 1 04 | 56 15 | 1.06666 | 56.250 | |
| 1 12 | 50 | 1.2 | 50 | superfluous, often omitted |
| 1 15 | 48 | 1.25 | 48 | superfluous, often omitted |
| 1 20 | 45 | 1.33333 | 45.000 | superfluous, often omitted |
| 1 21 | 44 26 40 | 1.35 | 44.4444 | |
| Note: | Babylonian mathematicians did | usually use zeros | but in few instances | |
| Note: | Babylonian mathematicians separated Base_60 powers by spaces or gaps. | Moderns sometimes use periods (.) |
Table 5. Reconstructed listing of the triplets on Tablet Plimpton 322
Triplet a,b,c & angle in degrees
from tablet Plimpton 232
prob. from Senkereh
ref.E.C. Zeeman
119,120,169, 44.8
3367,3456,4825,44.3
4601,4800,6649,43.8
***12709,13500,18548,43.3***
65,72,97,42.1
319,360,481,41.5
2291,2700,3541,40.3
799,960,1249,39.8
481,600,769,38.7
4961,6480,8161,37.4
3,4,5,37.4
1679,2400,2929,35.0
161,240,289,33.9
1771,2700,3229,33.3
28,45,53,31.9
175,288,337,31.3 Subroutine Template 1, division of quantity by two or more given ratios
# adapted from tcl-wiki Stats 2011-05-22, arithmetic mean [RLE]
#
# ::math::quantity_into_ratios --
#
# Return the division of quantity by two or more given ratios
#
# Arguments:
# val first value is quantity
# args other values are two or more given ratios
#
# Results: parts of quantity divided by ratios
#
proc ::math::quantity_into_ratios {quantity args} {
set sum 0.
set N [ expr { [ llength $args ] + 1 } ]
if { $N == 1 } { return 0 }
foreach val $args {
set sum [ expr { $sum + $val } ]
}
foreach val $args {
lappend answer [ expr { $quantity * ($val/$sum) } ]
}
set answer
}
#puts " ::math::quantity_into_ratios ( 84 2 2 2 ) answer 12.0 24.0 48.0 "
#puts " [ ::math::quantity_into_ratios 84 1 2 4 ] "
#puts " [ ::math::quantity_into_ratios 84 ] for (::math::quantity_into_ratios 84) returns zero "Subroutine Template 2, sqrt_sum_of_squares
# pretty print from autoindent and ased editor
# easy eye calculator, large black type on green
# used as testbed for one liners programs
# written on Windows 10 on TCL
# working under TCL version 8.6
# gold on TCL WIKI , 10Sep2020
package require Tk
package require math::numtheory
package require math::constants
package require math::trig
package require math
namespace path {::tcl::mathop ::tcl::mathfunc math::numtheory math::trig math::constants }
# adapted from tcl-wiki Stats 2011-05-22, arithmetic mean [RLE]
#
# sqrt_sum_of_squares --
#
# Return the sqrt_sum_of_squares by one or more
#
# Arguments:
#
# args other values are one or more
#
# Results: sqrt_sum_of_squares
#
proc math::sqrt_sum_of_squares { args} {
set sum 0.
set N [ expr { [ llength $args ] + 1 } ]
if { $N == 1 } { return 0 }
foreach val $args {
set sum [ expr { $sum + $val*$val } ]
}
set answer [ expr { sqrt($sum) } ]
}
#puts " ::math::sqrt_sum_of_squares ( 2 2 2 ) answer [sqrt 12 ]
# 3.4641016151377544
#puts " [ ::math::sqrt_sum_of_squares 1 2 4 ] "
#puts " [ ::math::sqrt_sum_of_squares 2 ] for ( ) returns zero "
console show
console eval {.console config -bg palegreen}
console eval {.console config -font {fixed 20 bold}}
console eval {wm geometry . 40x20}
console eval {wm title . " Console wrapper for sqrt_sum_of_squares "}
console eval {. configure -background orange -highlightcolor brown -relief raised -border 30}
puts " sqrt_sum_of_squares 2 2 2 equals [ math::sqrt_sum_of_squares 2 2 2 ]"
puts " sqrt_sum_of_squares 1 1 1 equals [ math::sqrt_sum_of_squares 1 1 1 ]"
puts " sqrt_sum_of_squares 1 1 equals [ math::sqrt_sum_of_squares 1 1 ]"
puts " sqrt_sum_of_squares 1 equals [ math::sqrt_sum_of_squares 1 ]"
puts " sqrt_sum_of_squares 0 equals [ math::sqrt_sum_of_squares 0 ]"output for sqrt_sum_of_squares
sqrt_sum_of_squares 2 2 2 equals 3.4641016151377544 sqrt_sum_of_squares 1 1 1 equals 1.7320508075688772 sqrt_sum_of_squares 1 1 equals 1.4142135623730951 sqrt_sum_of_squares 1 equals 1.0 sqrt_sum_of_squares 0 equals 0.0
Subroutine Template 3, quantity_into_multiple_ratios
# pretty print from autoindent and ased editor
# quantity_into_ratios for math::stats? package
# working under TCL version 8.6
# console program written on Windows 10 on TCL
# gold on TCL WIKI, 2Mar2017
package require Tk
console show
package require math::numtheory
namespace path {::tcl::mathop ::tcl::mathfunc math::numtheory }
set tcl_precision 17
# adapted from tcl-wiki Stats 2011-05-22, arithmetic mean [RLE]
#
# ::math::quantity_into_ratios --
#
# Return the division of quantity by two or more given ratios
#
# Arguments:
# val first value is quantity
# args other values are two or more given ratios
#
# Results: parts of quantity divided by ratios
#
proc ::math::quantity_into_ratios {quantity args} {
set sum 0.
set N [ expr { [ llength $args ] + 1 } ]
if { $N == 1 } { return 0 }
foreach val $args {
set sum [ expr { $sum + $val } ]
}
foreach val $args {
lappend answer [ expr { $quantity * ($val/$sum) } ]
}
set answer
}
# end of working deck
# add cosmetics below to bottom of file
console show
console eval {.console config -bg palegreen}
console eval {.console config -font {fixed 20 bold}}
console eval {wm geometry . 40x20}
console eval {wm title . " Console wrapper for quantity_into_ratios proc"}
console eval {. configure -background orange -highlightcolor brown -relief raised -border 30}
puts " Console wrapper for quantity_into_ratios proc"
puts " Return the quantities from list of ratios"
puts " [ ::math::quantity_into_ratios 84 2 2 2 ] "
puts " for ::math::quantity_into_ratios 84 2 2 2 returns 28.0 28.0 28.0 "
puts " for ::math::quantity_into_ratios 84 1 2 4 returns [ ::math::quantity_into_ratios 84 1 2 4 ] "
puts " for ::math::quantity_into_ratios 84 1 2 4 returns 12.0 24.0 48.0 "
puts " [ ::math::quantity_into_ratios 84 ] << for ::math::quantity_into_ratios 84 returns zero "
#end of deckprintout for quantity_into_ratios proc
Console wrapper for quantity_into_ratios proc Return the quantities from list of ratios 28.0 28.0 28.0 for ::math::quantity_into_ratios 84 2 2 2 returns 28.0 28.0 28.0 for ::math::quantity_into_ratios 84 1 2 4 returns 12.0 24.0 48.0 for ::math::quantity_into_ratios 84 1 2 4 returns 12.0 24.0 48.0 0 << for ::math::quantity_into_ratios 84 returns zero
Pseudocode, Equations, and Wiki Page Checklist
#pseudocode can be developed from rules of thumb.
#pseudocode: some problems can be solved by proportions (rule of three), to some order of magnitude
#pseudocode: enter quantity1, quantity2, quantity3 and expected output (quantity4) for testcases.
#pseudocode: enter time in years, number of remaining items
#pseudocode: output fraction of (remaining items) over (items at time zero)
#pseudocode: ouput remaining items as fraction or percent
#pseudocode: output fraction of (quantity4 ) over ( quantity1 at time zero)
#pseudocode: output fraction of (quantity2) * (quantity3 ) over (quantity1 at time zero)
#pseudocode: outputs should be in compatible units.
#pseudocode: rules of thumb can be 3 to 15 percent off, partly since g..in g..out.
#pseudocode: need test cases > small,medium, giant
#pseudocode: need testcases within range of expected operation.
#pseudocode: are there any cases too small or large to be solved?
Subroutine Template 4, geometric_mean
# pretty print from autoindent and ased editor
# geometric_mean for math::stats? package
# working under TCL version 8.5.6 and eTCL 1.0.1
# console program written on Windows XP on eTCL
# gold on TCL WIKI, 2Mar2017
package require Tk
console show
package require math::numtheory
namespace path {::tcl::mathop ::tcl::mathfunc math::numtheory }
set tcl_precision 17
# adapted from tcl-wiki Stats 2011-05-22, arithmetic mean [RLE]
console show
# ::math::geometric_mean --
#
# Return the geometric_mean of two or more values
#
# Arguments:
# val first value
# args other values
#
# Results:
# geometric_mean arithmetic geometric_mean value
proc ::math::geometric_mean { args } {
set product 1.
set N [ expr { [ llength $args ] } ]
foreach val $args {
set product [ expr { $product*$val } ]
}
set exponent [ expr { 1./$N } ]
set geometric_mean [ expr { $product**$exponent } ]
#puts " $N $exponent $product $args "
set geometric_mean
}
;# end of working deck
;# add cosmetics below to bottom of file
console show
console eval {.console config -bg palegreen}
console eval {.console config -font {fixed 20 bold}}
console eval {wm geometry . 40x20}
console eval {wm title . " Console wrapper for ::math::geometric_mean proc"}
console eval {. configure -background orange -highlightcolor brown -relief raised -border 30}
puts " Console wrapper for ::math::geometric_mean proc"
puts " Return the quantities from list of ratios"
puts " ::math::geometric_mean ( 1 2 3 4 ) answer 2.2133638 "
puts " [ ::math::geometric_mean 1 2 3 4 ] answer 2.2133638 "
Pseudocode on primes in Babylonian triplets
# pseudocode on Babylonian triplets
2m, m**2 - 1, m**2 + 1 Babylonian triplet
twin prime number.
twin prime numbers separated by 2,4,6 ...?
c**2= a**2 + b**2
c**2= a**2 + 1 normalized Babylonian triplet
a**2 = c**2 -1 normalized Babylonian triplet
some b and c are both primes.
some b and c are not both primes.
The reciprocal pair relationship.
(X+1/X)**2 - (X+1/X)**2 = 4 , divide equation by 4
normalized triplet, < (1/4)* ((X+1/X)**2 ) , 1 ,(1/4)* ((X+1/X)**2) >
0 < X-1/X < 2
1< X-1/X < 1+sqrt(2) ~~ approximate limit of 2.4
The Babylonian regular numbers between 0 and 60 have a limited set of triplets that
satisfy 1< X-1/X < 1+sqrt(2) which appears to be the role of Plimpton 322.
The limit 1< X-1/X < 1+sqrt(2) may explain the 1<X<2 limit on the Late Babylonian
many place reciprocal tablets.
d=6 even number, l = divisor of d**2 with integer result, Babylonian triplet method
a=l+b
b= d+ (d**2)//(2*l)
c= d+l+(d**2)/(2*l)
# supposed to work for all even dPossible Errors, Predefined Entries, Break Lines, Possible Wild_Cards in TCLLIB::math local copy
# Arguments:
# limit1 The limit for the largest prime to be included in the estimate
#
if { $limit1 <= 1 } {
return -code error "The limit must be larger than 1"
}
if { $limit2 <= 1 } {
return -code error "The upper limit must be larger than 1"
}
if { $n == 0 } {return 0}
if { $n < 1 } {return 0}
if { $n == 1 } {return 1}
if {$n<2} then {return -code return 2}
if {$n<4} then {return -code return 4}
if {$n<9} then {return -code return 9}
# forgivable error but no entry forwarded for calculation
if { [ isprime $limit3 ] < 1 } {
break
}
# Add the additional procedures to TCLLIB::math local copy
#
proc ::math::numtheory::call {args} {uplevel catch [list $args]}
proc ::math::numtheory::mathx { args } { set tcl_precision 17; puts [ expr [ expr { $args } ] ] }
;# translating Fortran and Qbasic control flow statements
proc ::math::numtheory::stop {} { return }
proc ::math::numtheory::end {} { exit }
proc ::math::numtheory::pause {} { wait .00010}
;# set comment lines from Fortran
proc ::math::numtheory::C {args} { set C # }
proc ::math::numtheory::REM {args} { set REM # } ;# attack of bots from Qbasic
proc ::math::numtheory::write {args} { puts $args }
proc ::math::numtheory::print {args} { puts $args } ;# attack of bots from Quickbasic
proc ::math::numtheory::SUBROUTINE {args} { proc $args }
proc ::math::numtheory::SUB {args} { proc $args } ;# attack of bots from Quickbasic
;# namespace eval ::math::constants {
variable constants {
pi 3.14159265358979323846 "ratio of circle circumference and diameter"
e 2.71828182845904523536 "base for natural logarithm"
ln10 2.30258509299404568402 "natural logarithm of 10"
phi 1.61803398874989484820 "golden ratio"
phi_2 0.61803398874989484820 "golden ratio conjugate"
tcl_precision_1 17 "tcl_precision number"
) set result {}
;# set list for calculation results
lappend result $number
}
return $resultTestcases Section
In planning any software, it is advisable to gather a number of testcases to check the results of the program.
Testcase 1
| table testcase 1 | printed in | tcl wiki format | |
|---|---|---|---|
| quantity | value | comment, if any | |
| set_number: | percent of prime numbers in set | percent primes in set of 10 over / set of N | |
| set 10 : | 44.44 | 1.0 | Modern base_10 |
| set 20 : | 42.10 | 1.05 | Archaic IndoEuropean base_20 |
| set 30 : | 34.48 | 1.28 | |
| set 40 : | 30.76 | 1.44 | |
| set 50 : | 30.61 | 1.45 | |
| set 60 : | 28.81 | 1.54 | Babylonian base_60 |
| set 70 : | 27.53 | 1.61 | |
| set 80 : | 27.84 | 1.59 | |
| set 90 : | 26.96 | 1.64 | |
| set 100 : | 25.25 | 1.76 | |
| set 110 : | 26.60 | 1.67 | |
| set 120 : | 25.21 | 1.76 |
Screenshots Section
Screenshots Section
figure 1a. Console wrapper for prime_formula proc
figure 1b, Console wrapper for sqrt_sum_of_squares
figure 1c, Console wrapper for sqrt_sum_of_squares
figure 1d, Market_Rate_Problem
figure 1e, Gauss Approximate Number of Primes
figure 2.
figure 3.
figure 4.
figure 5.
figure 6.
figure 7.
figure 8.
figure 9.
figure 10.
figure 11.
figure 12.
References:
- Primes
- Oneliner's Pie in the Sky
- One Liners
- Comparing Tcl and Python
- Primes Sieve - on a resizable canvas from uniquename
- TCLLIB ::math::numtheory
- https://en.wikipedia.org/wiki/Prime-counting_function
- http://sweet.ua.pt/tos/primes.html#i
- http://mathworld.wolfram.com/PrimeCountingFunction.html
- http://www.math.uni-bonn.de/people/jbuethe/topics/AnalyticPiX.html
- http://primes.utm.edu/notes/rh.html
- http://numbers.computation.free.fr/Constants/Primes/pixtable.html
- http://numbers.computation.free.fr/Constants/constants.html
- on line prime number generator, see
- http://www.miniwebtool.com/list-of-prime-numbers/?to=50
- Mathematician pair find prime numbers aren't as random as thought, March 15, 2016 by Bob Yirka,
- ref Robert Lemke Oliver and Kannan Soundararajan, Stanford University
- google < Prime number theorem Wikipedia >
- Probability that a number is prime, John D. Cook, 6 October 2010
- Probability of Next Prime Digit, Kevin's Math Page, Kevin Gong,March 17th, 2016
- Mathematicians Discover Prime Conspiracy, Erica Klarreich , March 13, 2016, Quanta Magazine
- Prime Probability: Catch the Wave, Michael M. Ross , Excel spreadsheet, Jan2008
- Prime Numbers and Their Statistical Properties,Dr. Phillip M. Feldman
- 19TH CENTURY MATHEMATICS - GAUSS, The Story of Mathematics
- A Conjecture about the Density of Prime Numbers,
- Lincoln Almir AMARANTE RIBEIRO, Departamento de Física,
- Universidade Federal de Minas Gerais, good explanation
- Dan Rockmore Stalking the Riemann Hypothesis, The Quest to Find the Hidden Law of Prime Numbers
- J. Pintz. On Legendre's prime number formula. Amer. Math. Monthly 87 (1980)
- Dusart, Pierre. Estimates of some functions over primes without r.h
- Ref. proc sum_primes_to by dkf
- from Comparing Tcl and Python on TCL WIKI
- Ref. Sieve of Eratosthenes « Python recipes « = code.activestate.com/recipes/117119/
References:
- Wikipedia search engine < TCL programs >
- Wikipedia search engine < TCL introduction >
- Wikipedia search engine < prime number >
- Google search engine < prime number formulas >
- Seaching for Babylonian Triplets Slot Calculator Example
- Gauss Approximate Number of Primes and eTCL demo example calculator, numerical analysis
- KWJ in Monster Prime Predicting Formula
- http://scidiv.bcc.ctc.edu/math/pythagoras.html
- http://www.saltire.com/applets/pythag/incircle.html
- http://math.uic.edu/~fields/puzzle/triples.html
- http://rle-vlsi.mit.edu/people/gjcoram/triples.html
- http://bsuvc.bsu.edu/home/00lcsapp/maths460.html
- http://www.math.utah.edu/~alfeld/teaching/pt.html
- http://138.25.60.81/numericon/triples.html
- http://www.geom.umn.edu/~demo5337/Group3/ti4.html
- http://www-groups.dcs.st-and.ac.uk/~history/PrintHT/Babylonian_Pythagoras.html
- Daniel F. Mansfield , N.J. Wildberger.
- Plimpton 322 is Babylonian exact sexagesimal trigonometry.
- Historia Mathematica, August 2017 DOI: 10.1016/j.hm.2017.08.001
- Newsweek, Babylonian Tablet Could Hold Mathematical
- Secrets For Today's Researchers, Josh Lowe , 8/25/17
- Unexpected biases in the distribution of consecutive primes
- Robert J. Lemke Oliver, Kannan Soundararajan ,Department of Mathematics, Stanford University
- The Last Digit of Prime Numbers - Numberphile on Youtube
- Lecture on “Rock, paper, scissors in probability, Tadashi Tokieda
- Hardy-Littlewood conjectures.
- MATHEMATICS SCIENCE, A new pattern in primes, Shubashree Desikan, Hindu Times
- en.wikipedia.org wiki search on Tadashi_Tokieda
- https://www.ncbi.nlm.nih.gov articles/PMC4978288/
- Distribution of the units digit of primes, C. M. Ko, National Central University
- www.wired.com tadashi-tokieda-finds-startling-objects-in-plain-sight/
;# References ;# current TCLLIB routines in Math Module math::numtheory::numberPrimesGauss N math::numtheory::numberPrimesLegendre N math::numtheory::numberPrimesLegendreModified N math::numtheory::differenceNumberPrimesLegendreModified lower upper math::numtheory::listPrimePairs lower upper step math::numtheory::listPrimeProgressions lower upper step
Appendix Code
appendix TCL programs and scripts
Subroutine Template 5, prime_formula
# pretty print from autoindent and ased editor
# easy eye format, large black type on green
# used as testbed for one liners programs
# written on Windows 10 on TCL
# working under TCL version 8.6
# gold on TCL WIKI , 5/15/2021
package require Tk
package require math::numtheory
package require math::constants
package require math::trig
package require math
namespace path {::tcl::mathop ::tcl::mathfunc math::numtheory math::trig math::constants }
# adapted from tcl-wiki Stats 2011-05-22, arithmetic mean [RLE]
#
# prime_formula --
#
# Return the possible primes in list by one or more
#
# Arguments:
#
# args other values are one or more
#
# Results: prime_formula
#
proc prime_formula { args} {
set list_new [list ]
set N [ expr { [ llength $args ] + 1 } ]
if { $N == 1 } { return 0 }
foreach val $args {
lappend list_new [ expr { 16*$val + 15. } ]
}
return $list_new
}
# end of initial deck
# add cosmetics below to bottom of file
console show
console eval {.console config -bg palegreen}
console eval {.console config -font {fixed 20 bold}}
console eval {wm geometry . 40x20}
console eval {wm title . " Console wrapper for prime_formula proc"}
console eval {. configure -background orange -highlightcolor brown -relief raised -border 30}
puts " Console wrapper for prime_formula proc"
puts " Return the possible primes in list "
puts " formula < 7 11 13 14 > equals possible primes? [ prime_formula 7 11 13 14 ]"
Subroutine Template 6, Combined Market Rate formula
;# pretty print from autoindent and ased editor
;# easy eye console, large black type on green
;# used as testbed for one liners programs
;# written on Windows 10 on TCL
;# working under TCL version 8.6
;# gold on TCL WIKI , 10Sep2020
;# Babylonian Combined Market Rate V6
package require Tk
package require math::numtheory
package require math::constants
package require math::trig
package require math
namespace path {::tcl::mathop ::tcl::mathfunc math::numtheory math::trig math::constants }
;# adapted from tcl Stats 2011-05-22, arithmetic mean <RLE>
;# ::math::combined_market_rate --
;#
;# Return the combined_market_rate by one,two, or more given rates
;# market rate defined as quantity per price
;# or 1 over (price per quantity)
;#
;# Arguments:
;#
;# args values are one, two, or more given rates
;#
;# Results: combined_market_rate
;# works for positive numbers, negative numbers,
;# and mixed positive & negative numbers.
;# arg of zero returns zero
;# arg of null returns zero
;# filter foreach drops irregular zero elements from argument
proc ::math::combined_market_rate { args} {
set sum 0.
set N [ expr { [ llength $args ] } ]
if { $N == 0 } { return 0 }
if { $N == 1 || [ lindex $args 0 ] == 0 } { return 0 }
set res {};set counter2 0;
;# filter foreach drops irregular zero elements
foreach item $args {if {$item != 0 } {incr counter2 1; lappend res $item } }
set counter 0
foreach val $res {
set sum [ expr { $sum + 1./$val } ]
incr counter 1
}
set combined_market_rate1 [ expr { 1./(($sum*1.)/$counter2) } ]
return $combined_market_rate1
}
;# various testcases on combined_market_rate
;# puts [::math::combined_market_rate 0.5524 0.4807 0.42918 0.47846 ]
;# answer 0.48131 "
;# puts [ ::math::combined_market_rate .1 .2 .3 .4 ]
;# answer 0.192
;# ::math::combined_market_rate -.1 -.2 -.3 -.4
;# answer -0.192, correct
;# operator math formula follows
;# check [/ 1. [/ [+ [/ 1. -.1] [/ 1. -.2] [/ 1. -0.3 ] [/ 1. -0.4] ] 4. ] ]
;# returns -0.192, correct
;# puts " [ ::math::combined_market_rate .1 ] "
;# :math::combined_market_rate -.1 -.2 .3 .4
;# answer -0.4363636363636364
;# operator math formula follows
;# set check [/ 1. [/ [+ [/ 1. -.1] [/ 1. -.2] [/ 1. 0.3 ] [/ 1. 0.4] ] 4. ] ]
;# check equals -0.4363636363636364
;# puts " for (::math::combined_market_rates .1)
;# returns .1 "
;# ::math::combined_market_rate {}
;# null returns zero, correct.
;# ::math::combined_market_rate 0
;# arg 0 returns zero, correct.
;# addition dated 24sep2018
;# added filter foreach to remove zero's
;# irregular zeros,
;# test on zero's 0.1 0.0 0.0 0.2 0.3 0.4
;# returns 0.192 , correct
;# test on zero's 0.1 0.0 0.0 0.2 0.3 0.4
;# returns 0.192 , correct
# end of initial deck
# add cosmetics below to bottom of file
console show
console eval {.console config -bg palegreen}
console eval {.console config -font {fixed 20 bold}}
console eval {wm geometry . 40x20}
console eval {wm title . " Console wrapper for combined market rate proc"}
console eval {. configure -background orange -highlightcolor brown -relief raised -border 30}
puts " Console wrapper for combined market rate proc"
puts " Return the combined market rate from list "
puts " formula < 0.5524 0.4807 0.42918 0.47846 > equals market rate? [ ::math::combined_market_rate 0.5524 0.4807 0.42918 0.47846 ]"
puts " formula < 7. 11. 13. 14. > equals market rate? [ ::math::combined_market_rate 7. 11. 13. 14. ]"Hidden Comments Section
Please place any comments here, Thanks, gold 30Apr2021
| Category Numerical Analysis | Category Toys | Category Calculator | Category Mathematics | Category Example | Toys and Games | Category Games | Category Application | Category GUI |