One Line Procs Compendium V4
This page is under development. Comments are welcome, but please load any comments in the comments section at the bottom of the page. Please include your wiki MONIKER and date in your comment with the same courtesy that I will give you. Aside from your courtesy, your wiki MONIKER and date as a signature and minimal good faith of any internet post are the rules of this TCL-WIKI. Its very hard to reply reasonably without some background of the correspondent on his WIKI bio page. Thanks, gold 2/20/2024 update.
- Title: One Liners Procs Compendium V4
- Preface
- Important Note. Not a Replacement
- Introduction
- Equivalent One Liners V2
- Philosophy On One Liners Programs
- Not a Replacement for TCL Core
- Reposted Tips from AMG & GWM & Wiki for One Liners Programs
- Examples for Reposted Tips
- Pseudocode For Problem Setup
- if, if, and iffy Table
- Timing in Console programs as Conclusion
- Precompiled Code saves Computation Time over One Liners Programs
- Important Note
- Random Integer
- Random Dice and other Related Randoms
- Centigrade to Degrees Fahrenheit
- Draft One Liners Spares
- Rule of 72 for Doubling Money
- Interest Rates
- Borrowed One Liners from TCL Wiki
- One Line Replacement for List command on TCL Wiki
- Health Calculations in one line TCL procs
- Borrowed rounding Floating Point Statements from TCL Wiki
- Burrowed One Liners from www.codecodex.com/wiki
- Testing One Liners Programs for list_twin_primes V2
- Table Results on Twin Primes for 2,4,6,10 Separators
- 2021 Newsflash, TCLLIB has twin primes and cousin primes routines in TCLLIB:math ticket pipeline
- Bits and Pieces, Testing One Liner Programs
- Fortran Like "Call" Procedure
- Circle Area and Law of Cosines
- "Chance of" and rand() Conditions
- Linear Interpolation, logic tests for even - odd of positive numbers
- Decimal Equivalents to some Babylonian Math Tables
- Triangular Numbers
- Electrical Procs
- Age of the Earth from Lord Kelvin, history of science
- One Liner Approach to the Fibonaci series
- Proc Titles into Lists
- Advanced Topics, Dependent on TCLLIB Math library
- Simple Error as Percentage
- Time on One Liner Programs
- Advanced Topics: Figurate Polynomial Formulas for TCL Procs
- Table : Figurate Formulas and TCL Procs Table
- 2021 Newsflash, TCLLIB has Figurate Polynomial routines and sum of powers Formulas routines in TCLLIB:math ticket pipeline
- Advanced Topics: Polynomials, Sums of Powers, Symbolic Differentiation & Integration in Tcllib Calculus
- Advanced Topics: Math Functions and Constants
- 2021 Newsflash, Astronomers report Titius-Bode-Based Exoplanet Predictions
- Advanced Topics: Modeling Planetary Distances using Titius-Bode Law and other simple power formulas
- figure . Modeling_Planetary_Distances_log_plot_titius_bode
- figure . Modeling_Planetary_Distances_plot_titius_bode_vs_gaussin
- Draft for One Liner Program Approach to Validation
- Advanced Topic, Recursion with Logic
- Advanced Topic, Sum of Infinite Geometric Series
- Advanced Topics, Extra Credit, But Cited for Public Domain
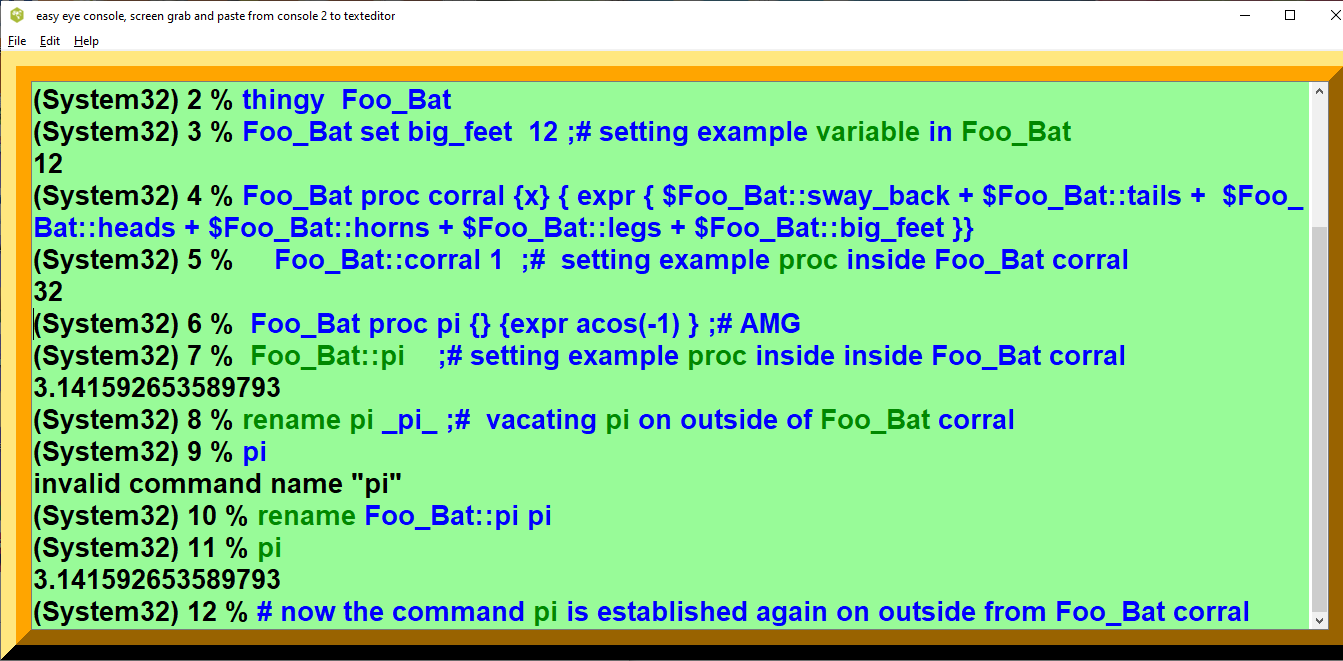
- Advanced Topic, One Liners Program Approach to OO Object Orientation system
- Easy Eye Testbed Session with thingy_RS & OO
- Observe Caution : Nesting Foo_Bats in Namespace Foo_Bat::Baby_Foo_Bat
- Figure 1 : Maddened Foo_Bat in Corral
- Figure 2 : thingy_OO action in Easy Eye Console Session screenshot 1
- Figure 3 : thingy_OO action in Easy Eye Console Session screenshot 2
- Figure 4 : Nesting Foo_Bats in Easy Eye Console Session screenshot 3
- Figure 5 : Refer to TCLLib section, Following Session is Dependent on TCLLIB Math library
- Draft One Liner Credits
- Credits on One Liner Programs
- References: Advanced Topics: Modeling Planetary Distances using Titius-Bode Law
- Appendix TCL programs and scripts
- Timing Equivalent One Liners V2
- Table of Timing 4 Procs
- Pretty Print Version
- Easy Eye Testbed for Thingy_RS and Other One Liner Programs
- Equivalent One Liners Programs using tiny_basic_RS.tcl
- Disclaimers and License
- Hidden Comments Section
Title: One Liners Procs Compendium V4
Preface
gold Update 2/29/2024 Here is extension of TCL article on One Liners Programs written for Wikipedia. Trying to boil down some gratis advice to me over 15 years of TCL Wiki membership. This page is intended to progress from simple questions to complex questions. Socrates held that wisdom was not current knowledge, but asking the right questions.
gold Update 2/29/2024. The author is retired engineer on Windows 10 and no longer has proofing access to Unix machines. Unix is respected after use of so many years in engineering, but my wings are lost. I did find a useful online IDE, jdoodle. I can paste from a text file, edit, and run an output using this online IDE.
Important Note. Not a Replacement
gold 6/8/2021 update. Important Note. This page were largely developed under the earlier TCL4, ETCL, and TCL8.~~ versions on an outdated personal computer. This page is not a replacement for the current TCL core and TCLLIB with much improvement since TCL4 and other <faster> language constructs. See better routines and current methods for angle reduction, sin, cos, pi, etc in the TCL core distribution and TCLLIB. As of Jul2018, the TCLLIB has developed code for trig angles in degrees, trig inverse, and hyper functions in degrees, and angle reduction in radians and degrees. This supplemental trig.tcl, trigtest.tcl, and trig.man code is posted on the TCLLIB website. This math::trig.tcl seems really exciting work, which will keep TCL in pace with some of the other brand name languages (math oriented, I mean). Some of the TCL library code is posted as pending on the TCLLIB website, and sometimes not really in the main TCL distribution yet, so its worthwhile to investigate and run searches on the pending TCLLIB code, the SourceForge bins, and [L1 ] locations also. The TCLLIB math library is generally quicker and more accurate by a third over some homebrew code, see math::mean , Additional math functions, [L2 ]. The numerous examples on this wiki page include code lines that might be incompatible, inefficient, dead_weights, or redundant if installed in the same program. As discussed below, the local math procedures in scripts and one-line procedures may not be as fast and efficient as importing mathop , mathfunc, and math from TCLLIB and SourceForge, so check with the precompiled code in the TCL core and TCLLIB libraries >> first <<, then homebrew your one liners programs and scripts in TCL.
gold 6/8/2021 update. We agree to some extent. These one line programs were developed mostly on older versions of TCL4 and eTCL. I do not doubt that alternate solutions, better and more elegant solutions exist on the later more elaborate TCL releases. Mostly I use the expired eTCL on an older outdated personal computer. Some of these single line procedures are easier to patch as an older TCL procedure rather than learn a new TCL grammar and pull the TCLLIB library. Naming no names as the TCL language versions and associated libraries get ever larger, one or two of these one liner programs were implemented on some smaller homebrew compilers without using the current massive TCL language. Reference the older Fortran and QuickBasic dogmas, I confess that habits brought from prior learned languages and dogmas in moldy Fortran textbooks of 50 years ago are hard to change.
Introduction
There is a gold mine of One Liners Programs and content in the Tool Control language TCL 8.6 core distribution, TCL manual pages, and TCLLIB library that can be adapted or recast into brief one liners programs. These one liners programs or procedures can be pasted into the TCL 8.6 console window for quick results, reference the TCL Wiki. Some one liners programs use the return statement, return $value, or return 1 to return the results to the program line. Although many TCL programmers just rely on the last computation being returned by the one liner procedure in the TCL console window. There is some room in the Wiki publications for programming style differences. But it is usually best to put usage, credits, or TCL documentation references for the one liners procedures on separate comment lines. The random rand procedures make use of the random function and do not return the same answer every time. Dependence on math operator notation, helper procedures, math check examples, and special library functions should be noted in the comment lines.
The terms program, routine, subroutine, procedure, and proc are used interchangeably in this article. Recognize that the TCL nomenclature uses the exceptional term procedure and proc, but the internet search engines and general public do not accept or pull the terms procedure and proc as equitably with respect to the other computer languages using terms subroutine and program.
There are pros and cons to one liner programs in TCL. One may contrast the approach to one liners programs in problem solving versus the traditional procedural approach. There are better routines and methods in faster language constructs in the current TCL core distribution and TCLLIB. Working with recursion, primes, text search, and timing the procedures will quickly show the warts on the one liners programs. To gain speed and shorter computation times, one will generally have to access the TCL core distribution and TCLLIB. Since the TCL interpreter collapses the carriage returns, skips, blank lines, and dead space of traditional written procedures into a single line of machine code, is not every script a one liner program to the parser? As grandfather remarked, the gourmet omelet, beef mulligan stew, and farm buttermilk all go to the same place.
The analogy of using a one liners program to control the large TCL language is like sticking an Apple computer for the human operator in front of a Cray computer. The human mind probably can only understand and use a limited set of instructions.So an interface in hardware or TCL language as a limited set of instructions or limited window of interaction might be useful. After all, the human mind was designed to chase rabbits. Reference the article on Little L Programming Language, Let's assign with let, and the L-Language pdf L , by Larry McVoy: See article on using Apple computers with Cray designer in Apple Cray Computer [L3 ].
Equivalent One Liners V2
Beginning in the sixties, the one liner program was typed input to the command line of an operating computer system terminal so that the one line command performs some useful function in a single one line of terminal input. Some of the original one liner commands were limited to a 60 character display on especially the early Basic terminals or to a 72 characters on the Fortran punched cards. Of course, the hit return to send, terminal flashing bulbs, and automatic answer back were silently understood as part or supporting the one liner program. Some of the line lengths in some computer languages were later extended to 120 characters and so on. The definition and use of the one liner program has been widened to include program source for any language that does something useful in one line. On batch programs, controlling and setting variable statements like RETURN, STOP, END, extra terminal prompts, and setting initial variables were used in Fortran systems. Of course, a very good feature of TCL is that new variables as number types do not have to be initialized prior to use and no subroutine RETURN and END statements are necessary, vis the older Fortran and Basic dogmas in moldy textbooks. Repeating, setting a new number variable to 0 or 1 is not necessary prior to using the variable. Good programming practice holds that one partial goal of computer programming is to produce human readable code. So it is permissible on the published console batch programs here to retain some vestigial stages to aid human comprehension. As a friendly challenge, the user is free to pare down the one liners programs even more. Meaning the user may omit the return statements, modify or omit the expr statements, switch to math operations mode, switch to TCLLIB precompiled code, and pull extra brackets for his own TCL version and setup.
Philosophy On One Liners Programs
I remember when my teenage sister would ask about a math problem. I would lead up and carefully explain this and that algebra proposition. But my sister would say " I just want the answer!" In most engineering problems, there is an advantage in finding the answer in an approximate solution, say slide rule accuracy or 4 significant places. For example, using the old slide rule, one would make a preliminary pencil calculation and approximate answer to set the decimal point, before using the slide rule accuracy to 4 significant places. If one thinks of TCL as primarily as a graphical gui language, then the one liners programs are best used to check the preliminary math concepts. One liners programs and initial console programs are often used to check the math concepts and generate testcases before loading the calculator gui shell.
In planning any software, it is advisable to gather a number of testcases to check the results of the graphical user interface gui program. The results of the testcases are estimated using the hand calculations and then checked in the TCL gui calculator. Pseudocode and equations are developed from the hand calculations and theory. One liners procedures and small console programs are written to check or proof the alternate subroutines or procedures, rather than keeping the unblessed code and comment lines in the main gui calculator. Finally the improved or alternate subroutines are loaded into the gui calculator. The TCL gui or slot calculator is effectively a shell program to input entries, host calculation routines, maintain housekeeping procedures, and display results. Additional significant figures are used to check the TCL calculator, not to infer the accuracy of inputs and product reports.
Not a Replacement for TCL Core
gold 2/20/2024 update. This page on developing one line procedures is not a replacement for the current Tcl core and Tcllib, which is much improved since Tcl version 4, and other <faster> language constructs. math ops, Tcllib routines, and other compiled routines can reduce the cost of big-data tasks by about 1/3. The time savings of the core are not always obvious on small quantities of data, like 4 or 5 numbers. Performance of one-line programs may suffer degradation due to lengthy recursion calls, and may be limited by constraints on recursion. Dependence on math operator notation, helper procedures, math check examples, degradation due to lengthy recursion calls, and special library functions should be noted in the comment lines.
Reposted Tips from AMG & GWM & Wiki for One Liners Programs
The beginner TCL procedure on the pi circle constant was corrected to proc pi {} {expr acos(-1)} # AMG. One Liners Programs should avoid using temporary variables like {set temp 3.14:if {$temp=3.14} {return 1};return $temp}. Temporary variables may cause more time delay, more complication, and possible confusion to reader. The return value of a Tcl procedure is inherited from the return value of the last command to execute within that procedure. Therefore, many uses of the return command are redundant. If one insists on temporary variables, be aware that it is perfectly legal for a proc and a variable to have the same name. You could have said "set pi [pi]". For safety and efficiency, always be sure to brace your expr-essions! Heh, I neglected to brace my expression in [pi], but that's one of the extremely rare cases where it won't matter: no spaces, no substitutions. Bracing does two things: One, when the entire expression is a single word (single argument), it can be bytecode-compiled. Two, if substitutions are performed by expr only and not Tcl itself, injection attacks are prevented. Since the expr command has an internal if conditional, ? in a?b:c sic, try using the internal if <?> in expr rather than a separate IFstatement. Avoid using separate if statements and temporary variables for brevity. The args variable is also useful tool in one liners programs for inputting multiple data or lists of words. Another strategy is to keep track of possible error checks and testcases for low, middle, and high values over the range of operation of the oneliners program. An initial check for zero division or series start at one may be installed in the expr ? conditional. A simple credit for a one liner program may use a semicolon with comment sign <# > at statement end, which should not degrade program execution. Using the time function in TCL will give even more insights into one liners programs, also see Time. In One liners Programs Pie in the Sky, one can see the advice of GWM on the importance of timing your code and procedures. Usually, invoking math ops, TCLLIB library, and other precompiled libraries can save an average of 1/3 time over big data chores. The time savings are not always obvious on small quantities of data. Performance of one liners programs may suffer degradation due to lengthy recursion calls and limits on the number of procedure recursion calls. The shorter the script, the faster and more reliable is the script. Dependence on math operator notation, helper procedures, math check examples, degradation due to lengthy recursion calls, and special library functions should be noted in the comment lines. The examples on this wiki page include code lines that might be incompatible, inefficient, or redundant if installed in the same program. As discussed, the local math procedures in scripts and one-line procedures may not be as fast and efficient as importing mathop , mathfunc, and math, so check with the precompiled code in the TCL core and TCLLIB libraries first, then homebrew your one-line programs and scripts.
Niklaus Wirth suggested in Pascal that a programmer should not use one letter for naming variables, but preferred two or more letters for variables in programming. For the one line programs in TCL, believe that typos or errors in variables will be caught faster if $aa, $bb, or $rrr is used rather than a single letter. From both Fortran77 and TCL experience, these one letter variables in expressions can easily be misread or dropped by human lapses. Example code in Wiki would be far easier to understand if one picked variable names that related to the real-world values, names, and math terms. Absent external explanations and diagrams, the variables aa, bb , and cc in typical algebra formulas have no meaning. If the reader is without a detailed explanation, charts and diagrams, and variable definition list, therefore the real-world names themselves may help to guide a reader as to their meaning and use in program. (This is partly a rant from Anonymous on wiki, reformulated as a positive contribution to Reposted Tips.)
For example on variable name conventions, suppose one was given the three sides of triangle as a,b, and c. Or even worse, the triangle sides are listed in Greek letters alpha, beta, and delta. The task is to find side c, given the length of the other two sides from the Pythagorean formula cc**2 = aa**2 + bb**2. As a mercy to the reader, we are going to spell out the sides in algebraic terms rather than single letters. Set hypotenuse_side_cc**2 as expr { $adjacent_side_aa**2 + $opposite_side_bb**2}. So the solution as a one line proc would be proc Pythagorean_formula {adjacent_side_aa opposite_side_bb } { expr { sqrt ($adjacent_side_aa**2 + $opposite_side_bb**2)}}. Similar to the hypot command in TCL, the proc Pythagorean_formula returns 5 for the triangle sides of 3 and 4. However, the order of the sides in this case does not matter.
Examples for Reposted Tips
# procs below should should be pastable into TCL Console
proc pi {} {expr acos(-1)} # AMG
time {pi} 5000 # returns 0.6178 microseconds per iteration
proc pie {} {acos -1 } # braces may take place of expr expression
time { pie } 5000 # 0.5982 microseconds per iteration
proc pies {} [acos -1 ] # dropping expr expression in math ops; math op slightly improved time
time { pies } 5000 # returns 0.5846 microseconds per iteration
# use args for list of multiple inputs & return list of list of counts and values
proc multiple_pies {args} { foreach i $args {lappend res " count [incr $i ] for [acos $i] "}}
# Usage multiple_pies -1 -1 -1 -1 -1 -1 -1 -1 -1 # returns list of counts and values
time {multiple_pies -1 -1 -1} 3 # returns 2509 microseconds per iteration & list of counts & values
# sample multiple_pies printout => \n count 1 for 3.14 \n count 2 for 3.14 \n count 3 for 3.14
proc pq {} {set temp [ expr { acos(-1)} ] ; return $temp } # temporary variables not recommended
time {pq} 5000 # returns 0.6338 microseconds per iteration # temporary variables usually slow results
proc add {args} {return [ ::tcl::mathop::+ 0. {*}$args]} # using math ops and $args
# Usage add 1 2 3 4 5 6 7 8 9 returns 45
# suggest maintain dead spaces and air gaps near expr, brackets, etc in following statements
# example one liners program uses internal conditional in the expr command
proc errorx {aa bb} {expr { $aa > $bb ? (($aa*1.)/$bb -1.)*100. : (($bb*1.)/$aa -1.)*100.}}
# Usage errorx 3.1 3.14 returns error 1.2903 in positive percent
# variable naming conventions
set adjacent_side_aa 3.
set opposite_side_bb 4.
set hypotenuse_side_cc "unk"
proc Pythagorean_formula {adjacent_side_aa opposite_side_bb } { expr { sqrt ($adjacent_side_aa**2 + $opposite_side_bb**2)}}
set hypotenuse_side_cc [ Pythagorean_formula 3 4 ] # returns 5
# begin RS code in One liners program for basic style let in one line
proc let2 {_var expr} {upvar 1 $_var var;set var [uplevel 1 [list expr $expr]] } # RS
# Usage let2 a {999999} ; puts $a # returns 999999
# Usage let2 bombs without braces or brackets on widely spaced math expression
# Usage let2 a 4 * 9999 + 77777. # returns error should be "let2 _var expr"
# subbed $args into expr variable and bb as assignment symbol
# _var is assigned variable and args expression follows assignment operator ==
# $args in let3 can handle a widely spaced list <expression> unlike let2
# let3 working previously, but having troubles and sometimes buggy now
proc let3 {_var bb args} {upvar 1 $_var var;set var [uplevel 1 [list expr $args]] } # $args in RS derived
# Usage let3 a == [ expr 4 * 9999 + 77777. ] ; puts $a # returns 117773.0
# Usage let3 a == 4 * 9999 + 77777. ; puts $a # returns 117773.0Continuing Reposted Tips from Wiki. Not all problems have sufficient information or initial conditions to solve the problem. However, the analysis may develop low, high, and breakpoint constraints with a bag of assumptions from similar problems and testcases. The most consistent error check should be that the sum of the shares should equal the original total. The analogy of the process is ( egg >> chicken >> return to egg). In writing pseudocode: 1) need test cases for small,medium, giant metrics, 2) need testcases within range of expected program operation, and 3) are there any cases too small or large to be solved in the current constraints? With TCL/Tk canvas and Tk graphical capability, a graphical solution is usually a good alternative. At least, a graphical solution will give one some assurance on the math. In the case that several one liners programs are available or possible to solve a similar problem, a time averaging, weighted, or piecemeal solution can produce surprising and robust results towards a problem solution. Thanks to the Heisenberg's uncertainty principle, some solutions exist as a band or cloud of values between a lower limit or upper limit. The solution band for a double false position solution DFPP would be between < set false1 expr $guess * 3/5 and <set $false2 expr $guess * 4/5>. The center line between lower and upper solution bounds would be <false1 & false2> /2. For some tuffies with no obvious linear solutions, see [L4 ], [L5 ], [L6 ], and [L7 ]
gold 10/26/2020. Note from Ask13 [L8 ]. I have collected some tips on faster code for you. I have not seen your code. But Reposted Tips from AMG & GWM & Wiki and Continuing Reposted Tips from Wiki may be of help. One would almost have to do a time analysis of individual subroutines and individual lines to find the "core hogs" with the time command. See [L9 ] It is sometimes advantageous to write and divide the script into smaller subroutine chunks, organized and structured data code subsections for easier detection of "core hogs. See model [L10 ]. A "core hog" in a heap of straw and spaghetti code is more difficult to find, from experience here. Most programmers find it convenient to test or dry run a new subroutine or one liner program inside a testbed or separate console program. The new subroutine is exercised separately without invoking the whole main program or gui, graphical user interface. Some commercial testbeds are set with speed and performance markers. See sections Easy Eye Testbed and Timing Equivalent One Liners V2 below. Also refer to wiki page on Easy Eye Calculator and Playing Recursion V2 [L11 ].
Pseudocode For Problem Setup
# using pseudocode
# collect possible problem instances
# collect testcases over range of operation
# time averaging, weighted, random or linear piece wise solution
# can produce surprising and robust results
# possible modeling a 3ird or Nth order solution to
# 2nd order over expected range of operation
# possible normalize some parameters to 1
initialize algorithm_result = 1.
# desired_goal usually 1 unit or 100 square units in some early math problems
set false1 [expr $guess * 3/5]
set false2 [expr $guess * 4/5]
calculate f(false1) and f(false2)
solution band between false1 lower limit
and false2 upper limit
# recommended, avoid division or division by zero in one liners
center of solution band < f(false1) & f(false2) > * .5
double false position solution dfps
error1 = product -f1
error2 = product -f2
[expr (e2*f1-e1*f2)/(e2-e1)]
check algorithm
f(solution) =? initial product solution
check error , abs (desired_goal - current value) <=? $required_accuracy
check_sum = a+b+c+d+e = total of shares = original real estate = normalized 1
check_answer new answer =? desired goal , desired goal reached (yes/no)
yes = finished loop
set answers and printout with resulting values
pseudocode: need test cases > small,medium, giant
pseudocode: need testcases within range of expected operation.
pseudocode: are there any cases too small or large to be solved?if, if, and iffy Table
See section Noise Words of if by AMG. Seemed to call for a table, if one is studying recursion on one liner programs.
| table | printed in | TCL format | |
|---|---|---|---|
| elements | short hand for if | long hand for if | comment, if any |
| 2 | if a b | # if {a} then {b} | |
| 3 | if a b c | # if {a} then {b} else {c} | # 2*n+1 elements odd |
| 4 | if a b c d | # if {a} then {b} elseif {c} then {d} | |
| 5 | if a b c d e | # if {a} then {b} elseif {c} then {d} else {e} | # 2*n+1 elements odd |
| ***** | alternate | expressions for expr | **** |
| 8 | if a b c ...c1,c2,c3... d e | # if {a} then {b} elseif {c} ...elseif {c1} elseif {c2} elseif {c3} .... then {d} else {e} | maybe multiple successive elseif?, but not seen example |
| 3 | a?b:c | expr equivalent# if {a} then {b} else {c} # 2*n+1 elements odd | expr command has an internal if conditional ? in a?b:c |
| 5 | a?b:c?d:e | expr equivalent # 2*n+1 elements odd | expr command has an internal if conditional ? in a?b:c |
| 7 | a?b:c?d:e?f:g | expr equivalent # 2*n+1 elements odd | expr command has an internal if conditional ? in a?b:c |
| 9 | a?b:c?d:e?f:g?h:i | expr equivalent # 2*n+1 elements odd | expr command has an internal if conditional ? in a?b:c |
| 11 | a?b:c?d:e?f:g?h:i?j:k | expr equivalent # 2*n+1 elements odd | expr command has an internal if conditional ? in a?b:c |
Timing in Console programs as Conclusion
A console program has been modified to check the results and timing of one liner procedures in the script at bottom of page. The user can add new algorithms by adding a new one liners program in the source code. One add a number line to the if statement that controls the algorithm selection in the console program. The one liner procedures and solutions can also be pasted into the TCL console easily. There are some series for 1/N*N and 1/N*N*N*N which gives fractions of pi. Other functions for testing include Eulers double prime probability , pi generating series, the Monte Carlo random algorithms, and the strip integral of a quadrant. The accuracy of these individual solutions varies with the number of trials and some algorithms used are fairly slow, even glacial closers. Most of the one liners programs and usage examples should be pastable into the TCL console. Usually recommend the easy eye console with green screen and large type. A similar approach to timing one liners procedures may be seen in One Liners Programs Pie in the Sky and Counting characters in a string.
Precompiled Code saves Computation Time over One Liners Programs
# procs below should should be pastable into TCL Console
# returns logical on find element in list
# 1 or 0 for yes or no, using lsearch command
# Suggest maintain dead space and air gap around expr, brackets, etc
proc find_in_list {lister element} {expr {[lsearch -exact $lister $element] >= 0}} # Wiki Books TCLP
time {find_in_list {11 22 33} 22} 5000 # results in 0.6286 microseconds per iteration
# using lsearch cmd in precompiled code from TCL core
time {lsearch -exact {11 22 33} 22} 5000 # results in 0.2764 microseconds per iteration
# precompiled TCL code from TCL core & TCLLIB
# precompiled TCL core saves computation time about 60 percent here
# over one liners program
# following list2 proc equivalent to list command
proc list2 args {set args} # Wiki Books TCLP
time { list2 TCL must avoid unbalanced quotes or braces } 5000 # results in 0.4576 microseconds per iteration
# using list cmd in precompiled code from TCL core
time { list TCl must avoid unbalanced quotes or braces } 5000 # results in 0.0986 microseconds per iteration
# precompiled TCL core saves computation time about 80 percent here
# from one liners programImportant Note
{gold] 15Sep2020. Important Note. This page is not a replacement for the current TCL core and TCCLIB with much improvement since TCL4 and other <faster> language constructs. See better routines and current methods for angle reduction, sin, cos, pi, etc in the TCL core distribution and TCLLIB. As of Jul2018, the TCLLIB has developed code for trig angles in degrees, trig inverse, and hyper functions in degrees, and angle reduction in radians and degrees. This supplemental trig.tcl, trigtest.tcl, and trig.man code is posted on the TCLLIB website. This math::trig.tcl seems really exciting work, which will keep TCL in pace with some of the other brand name languages (math oriented, I mean). Some of the TCL library code is posted as pending on the TCLLIB website, and sometimes not really published in the main TCL distribution yet, so its worthwhile to investigate and run searches on the pending TCLLIB code also.
Random Integer
# random integer in the range zero to $nn
# one liner uses the expr calculation method
proc random_number_less_than nn { expr { int($nn * rand())}}
# Usage random_number_less_than 10
# may return 3, 8, 9 or other random numberRandom Dice and other Related Randoms
gold 2/20/2024 update. The random pick algorithm was posted by Suchenworth RS on Horseracing in Tcl. Using the random pick algorithm from Suchenworth RS is an alternate way to simulate dice play and sometimes easier for the non standard dice set ups. Other dice pages are Throwing Two Dice GWM and Dice by Keith Vetter. Also int from RLE has dice expression expr {1 + int(rand()*6)} RLE. Several Dr. Math emails may reduce some dice issues to simple paths. Another useful wiki page was Counting Elements in a List from RWT.
# Random Dice & alternate procedures, checking math and format here
# Original base expression is expr {1 + int(rand()*6)} RLE
# check parens? weak eyes here.
proc dice_sides_N { dice_sides } { expr { 1 + int(rand()*$dice_sides)} }
proc dice_sides_N { dice_sides } { expr { 1 + int(rand()*$dice_sides)} }
# Computes optimum for Dragon Counting Game from James Munro, Oxford mathematician
proc optimum_N { dice_sides } { expr { int(1.718281828 *$dice_sides) }}
# Alternate gimmick and fudge constant under test
proc optimum_G { dice_sides } { expr { int(1.6180339887498948420 *$dice_sides) }}
# set g_constant .6180339887498948420
# golden ratio is 1.6180339887498948420 Centigrade to Degrees Fahrenheit
# following one liners use math operator notation
# degrees Centigrade to degrees Fahrenheit
proc Fahrenheit cc { [+ [* 1.8 $cc] 32. ]}
# Usage Fahrenheit 20 returns 68. degrees Fahrenheit
# degrees Fahrenheit to degrees Centigrade
proc Centigrade ff { [/ [- $ff 32. ] 1.8 ]}
# Usage Centigrade 68 returns 20 degrees centigradeDraft One Liners Spares
# Reference Tcl 8.4 Built-In Commands - expr manual page
# random integer in the range 0. zero to $nn
proc random_number_less_than nn { expr { int($nn * rand()) } }
# Usage random_number_less_than 10
# may return 3 or other random number
# random_number_less_than 0 returns 0
# random_number_less_than 1 returns 0, on clipping $nn
# Reference Tcl 8.4 Built-In Commands - expr manual page
# convert cartesian coordinates into polar coordinates:
# convert from ($x,$y)
proc radius {y x} { expr { hypot($y, $x) } }
proc angle {y x} { expr { atan2($y, $x) } }
# Usage radius 1 1 returns 1.414 or square root 2
# Usage angle 1 1 returns 0.785
# Reference Tcl 8.4 Built-In Commands - while manual page
proc print_out nn {set x 0; while {$x<$nn} { puts " number $x"; incr x}}
# Usage print_out 2 returns number 0, number 1
# Reference Tcl 8.4 Built-In Commands - foreach manual page
proc list_numbers {} { set lister {}; foreach {i j} {1 2 3 4 5} { lappend lister $j $i}; return $lister}
# list_numbers returns 2 1 4 3 {} 5
# Tk8.6.10 Documentation > Tcl Commands > for
#; www.tcl-lang.org/man/tcl8.6/TclCmd/for
proc powers_of_two nn { for {set x 1} {$x<=$nn} {set x [expr {$x * 2}]} { puts "x is $x"}}
# Usage powers_of_two 2 returns x is 1; x is 2
# Usage powers_of_two 1024 returns x is 1; x is 2;..... x is 1024
# following use math opsRule of 72 for Doubling Money
These one liners programs were developed from articles and research on Interest Rates [L12 ]. Also [L13 ] [L14 ] [L15 ] [L16 ]
# compute the doubling time constant in years for money
# using interest rate in percent for exact constant
proc rule_72_constant {percent } { expr { log( 2. )/ log (1. + $percent/100.)} }
# Usage rule_72_constant 10 returns 7.27253 years,
# 7.27253 years to double money at 10 percent interest
# setting the doubling constant at 10* 7.27253 percent rounds to 72.
proc approximate_doubling_time {percent} { expr { 72. / $percent}}
# example 1, { expr {72./10 }} approximates 7.2 years
# example 2, { expr {72./4 }} approximates 18 years
# money at 4 percent doubles about 18 yearsInterest Rates
These one liners programs were developed from articles and research on Old Babylonian Interest Rates [L17 ]. Also [L18 ] [L19 ] [L20 ] [L21 ]
# These statements should be pastable into the easy eye console.
# ***** simple interest problems in TCL one liners procedures *****
# find simple interest amount from 3 entries as < principal interest years >
proc simple_interest_amount { principal interest years } { expr { ($principal*1.)*(1.+$years*$interest )}}
# Usage simple_interest_amount 5000. .05 7. returns 6750.0
# find simple interest principal from 3 entries as < amount interest years >
proc simple_interest_principal { amount interest years } { expr { ($amount*1.)/(1.+$years*$interest )}}
# Usage simple_interest_principal 6750.0 .05 7. returns 5000.0
# find simple interest rate from 3 entries as < amount principal years >
proc simple_interest_rate { amount principal years } { expr { ((($amount*1.)/$principal)-1.)/$years }}
# Usage simple_interest_rate 6750.0 5000. 7. returns 0.05
# find years of simple interest from 3 entries as < amount principal interest >
proc simple_interest_years { amount principal interest } { expr { ((($amount*1.)/$principal)-1.)/$interest }}
# Usage simple_interest_years 6750.0 5000. .05 returns 7.0
# ****** compound interest problems in TCL one liners procedures ******
# find compound interest amount from 4 entries as < principal interest years compounding_times_per_year >
# cd is compounding times per year, usually 4 quarters or 12 months
proc compound_interest_amount { principal interest years cd } { expr { ($principal*1.)*((1.+( $interest /$cd))**($years*$cd))}}
# Usage compound_interest_amount 5000 .05 7 12 retuRns 7090.180
# find compound interest principal from 4 entries as < amount interest years cd >
# cd is compounding times per year, usually 4 quarters or 12 months
proc compound_interest_principal { amount interest years cd } { expr { $amount*( 1. +(($interest*1.)/$cd ) )**(-1.*$cd*$years)}}
# Usage compound_interest_principal 7090.180 0.05 7 12 returns 4999.997, rounds to 5000.
# find interest in compound interest from 4 entries as < amount principal years cd >
# cd is compounding times per year, usually 4 quarters or 12 months
proc compound_interest_interest { amount principal years cd } { expr { $cd*((($amount*1.0)/$principal)**(1./($cd*$years))-1.)}}
# Usage compound_interest_interest 7090.180 5000. 7 12 returns 0.049, rounds to 0.05
# find years of compound interest from 4 entries as < amount principal interest cd>
proc compound_interest_years { amount principal interest cd } { expr { (log10 (($amount*1.0)/$principal)) / ($cd*log10(1.+(($interest*1.)/$cd) ) ) }}
# Usage compound_interest_years 7090.180 5000. 0.05 12 returns 6.99, rounds to 7 years
# ******** continuous_compounding ******* based on exponential formulas and natural log.
proc amount_continuous_compounding { principal interest years } { expr { $principal* exp ( $interest*$years*1. ) }}
# Usage amount_continuous_compounding 5000. 0.05 7 returns 7095.3377
proc principal_continuous_compounding { amount interest years } { expr { $amount * exp ( $interest*$years* -1. ) }}
# Usage principal_continuous_compounding 7095.33 0.05 7. returns 4999.994, rounds to 5000.
proc interest_continuous_compounding { amount principal years } { expr { (log ( ($amount*1.) /$principal )) / ($years * log (exp(1.) ) ) }}
# Usage interest_continuous_compounding 7095.33 5000. 7 returns 0.04999, rounds to 0.05
proc years_continuous_compounding { amount principal interest } { expr { (log ( ($amount*1.) /$principal )) / ($interest * log (exp(1.) ) ) }}
# Usage years_continuous_compounding 7095.33 5000. 0.05 returns 6.999, rounds to 7 years
proc eckart–mchale_69p3 {rate} { return [expr {(69.3/$rate) * (200./(200.-$rate))} ] }
# 2nd order eckart–mchale, 20 percent interest rate doubles money in how many years?
# Usage eckart–mchale_69p3 20.0 # returns 3.85
# 2nd order solution, should be not that far from exact 3.802.
proc pade_rule_69.3 { rate } { return [ (69.3/$rate) * (600.+4.* $rate)/(600.+$rate) ] }
# pade_rule 20 percent interest rate doubles money in how many years?
# Usage pade_rule_69p3 20.0 # returns 3.8
# 3ird order solution, should be not that far from exact 3.802
# following exact doubling rule etc in TCL using natural logarithms.
# Denominator term < log (1.+ $rate/100.)> represents Principle and Interest P&I
# Manipulating log term in nominator, log (2) for doubling,
# and log (3) for tripling, log (1.5) for 50% (factor >.5<) rise.
# extensions log (5) for 5X, log (10) for 10X, log (16) for 16X, etc.
proc exact_doubling_rule { rate } { return [ expr { log (2.) / log (1.+ $rate/100.)}] }
# what is computation times (years here),
# to double amount at interest rate of 20 percent
# Usage <exact_doubling_rule 20. > returns 3.8017 years
proc exact_tripling_rule { rate } { return [ expr { log (3.) / log (1.+ $rate/100.)}] }
# what is computation times (years here),
# to triple amount at interest rate of 20 percent
# Usage <exact_tripling_rule 20 > # returns 6.0256 years
proc exact_rise_rule { rate } { return [ expr { log (1.5) / log (1.+ $rate/100.)}] }
# what is computation times (years here),
# to rise amount 50 percent (>.5< factor below)
# at interest rate of 20 percent
# Usage <exact_rise_rule 20. > # returns 2.2239 years
Borrowed One Liners from TCL Wiki
Reference FW and RS on Plain string substitution in Bag of algorithms, also Example Scripts Everybody Should Have
proc plainsub {text item replacewith} { set text [string map [list $item $replacewith] $text]} # RS derived
# Usage plainsub {The quick brown fox jumped over the fences.} fox cat
# returns The quick brown cat jumped over the fences.
# Usage plainsub {123456789} 3 * returns "12*456789"
# Usage plainsub 123456789 3 1 returns "121456789"
proc commify number {regsub -all {\d(?=(\d{3})+($|\.))} $number {\0,}} # Peter Spjuth
# Usage commify {123456789} returns 123,456,789
# begin RS code
# One liners program for
# basic style let in one line
proc let {_var expr} {upvar 1 $_var var;set var [uplevel 1 [list expr $expr]] } # RS
# Usage let a {999999} ; puts $aOne Line Replacement for List command on TCL Wiki
proc Lister args {set args}Health Calculations in one line TCL procs
Conversion unit formulas in one line TCL procs. Refer tp [L22 ] & [L23 ]
# conversion unit formulas in one line TCL procs
# HOMA-IR standing for Homeostatic Model Assessment of Insulin Resistance
# HOMA_IR = expr { $insulin * $glucose * $scale_factor}
# fasting blood insulin in units uIU/mL
# fasting blood glucose in units mg/dL
proc HOMA_IR2 { insulin glucose } {
set scale_factor [ expr { 1. / 405. } ]
return [expr { $insulin * $glucose * $scale_factor}]}
# HOMA-IR calculations here requires U.S. standard units.
# European SI units as best understood.
# To convert component terms of HOMA-IR ( $insulin & $glucose)
# from international S.I. units:
# Insulin: pmol/L to uIU/mL, divide by (÷) 6
# Glucose: mmol/L to mg/dL, multiply by (x) 18
# hbA1c_convert_to_average_blood_glucose mg/dl HbA1c
# HbA1c test is a simple blood test that measures your
# average blood sugar levels over the past 3 months.
# As a peg point, 5 HbA1c units converts to 100 mg/dl,
# mg/dl is abbreviation for milligrams per deciliter.
proc a1c hbA1c { expr { 35.6*$hbA1c -77.3} }
# convert mg/dl to mmol/L average blood glucose
# European SI units conversion on blood glucose
# some papers round off 18.016 to mgdl/18.
proc mgdl_to_mmoll mgdl { expr { $mgdl/18.0 } }
# convert mmol/L to mg/dl average blood glucose
proc mmoll_to_mgdl mmoll { expr { $mmoll*18.0 } }
# formula QUICKI_index insulin resistance = 1/(log(insulin) + log(glucose)), decimal logs
proc QUICKI_INDEX_IR { insulin glucose } { return [ expr { 1./(log10($insulin) + log10($glucose))} ] }
# Usage set answer [ QUICKI_INDEX_IR 4. 100. ] # eval 0.38 # conversion unit formulas in one line TCL procs
# body mass index in metric units, persons weight in kilograms, height in meters
proc body_mass_index_BMI { weight height } { return [ expr { (1.* $weight ) / ( $height * $height)} ] }
# metric testcase, weight is 64 kg and height is 1.9 meters tall.
set answer [ body_mass_index_BMI 64. 1.9 ] #; evals to 17.728, rounds to BMI of 17.7
# formula in English units, BMI = ( 703. X weight_in_pounds ) / ( height_in_inches * height_in_inches )
proc body_mass_index_BMI_lbs { weight height } { return [ expr { (703.* $weight) / ( $height * $height ) } ] }
# testcase 58 inches , 100 pounds, BNI = 21., proc returns 20.897, rounds to 21.
set answer [ body_mass_index_BMI_lbs 100. 58. ] # total daily calories from carbohydrates, proteins, and fats, all entries in grams
# Carbs provide 4 calories per gram,
# protein provides 4 calories per gram, and fat provides 9 calories per gram.
proc total_daily_calories { carbs proteins fats } { return [ expr { 4. * $carbs + 4. * $proteins + 9. * $fats } ] }
# testcase from daily keto diet, 20 grams carbs, 80 grams protein, and 150 grams fats and oils
# Usage,
set carbs 20. ; set proteins 80. ; set fats 150.
set answer [ total_daily_calories $carbs $proteins $fats ] # returns 1750 calories Borrowed rounding Floating Point Statements from TCL Wiki
gold 7/15/2021. I borrowed some floating point rounding statements circa 2004 from AM and pooryorick in wiki page Floating-point formatting, Rounding in Tcl & round to write the proc precisionx in Blood+Glucose in 20aug2020 [L24 ]. This may not qualify as one line program by some standards, but has been so useful in the Tcl calculators, that I can hardly leave it out of the compendium. Rererence article on floating point pitfalls [L25 ].
# proc precisionx used to round off floating point numbers
set precision 5.
set float 3.000000000001
set test_float_2 3.999999999997
set x [ expr {round( 10 ** $precision * $float) / (10.0 ** $precision)} ] # <AM>
proc rnd_floating_pt {precision float} { expr {round( 10 ** $precision * $float) / (10.0 ** $precision)}} # <AM>
set float $test_float_2
proc precisionx {precision float } {
# tcl:wiki:Floating-point formatting, <AM>
# select numbers only, not used on every number.
set x [ expr {round( 10 ** $precision * $float) / (10.0 ** $precision)} ]
# rounded or clipped to nearest 5ird significant figure
set x [ format "%#.5g" $x ]
return $x
}# list of TCLLIB rounding commands ::math::decimal::round_half_even decimal digits ::math::decimal::round_half_up decimal digits ::math::decimal::round_half_down decimal digits ::math::decimal::round_down decimal digits ::math::decimal::round_up decimal digits ::math::decimal::round_floor decimal digits ::math::decimal::round_ceiling decimal digits ::math::decimal::round_05up decimal digits
Burrowed One Liners from www.codecodex.com/wiki
#under test from www.codecodex.com/wiki
set lister { 1 2 4 5 6 7 8 9 10 }
set s {starchild}
package require struct::list
proc reverseWords s {return [struct::list reverse [split $s]]}
proc ! n {expr {$n<2? 1: $n*[! [incr n -1]]}}
# Usage ! 5 returns 120
# Suggest maintain dead space and air gap around expr, brackets, etc
proc average list {expr ([join $list +])/[llength $list].}
for {set i 1} {$i <= 1000} {incr i} {pust [expr {$i*($i+1)/2}]}
namespace import ::tcl::mathop::*
proc average list {expr {[+ {*}$list]/double([llength $list])}}
# works here , average $lister returns 5.777777777777778
proc fib n {expr {$n<2? $n: [fib [incr n -1]] + [fib [incr n -1]]}}
# not working here
namespace import ::tcl::mathfunc::*
::tcl::mathfunc::isqrt 25
# ::tcl::mathfunc::isqrt 25 returns 5, working here
set date [clock format [clock scan $date] -format {%Y-%m-%d %H:%M:%S}] # dclaar
scriptEval clock format [clock scan $tDate] -format {%Y-%m-%d %H:%M:%S} # dclaar
# clock scan is your friend; it knows all sorts of formats. In
# case above, it converts: Oct 15 06:52:45 2009 to: 2009-10-15 06:52:45Testing One Liners Programs for list_twin_primes V2
# pretty print from autoindent and ased editor
# list_twin_primes V2
# written on Windows 10 on TCL
# working under TCL version 8.6
# gold on TCL Club , 8/20/2020
# Ref. WIKI BOOKS, Tcl_Programming_Introduction
# Book Section contrasts one liners
# versus traditional procedural approach
# below contains redundant procs
package require Tk
package require math::numtheory
package require math::constants
package require math::trig
package require math
namespace path {::tcl::mathop ::tcl::mathfunc math::numtheory math::trig math::constants }
set tcl_precision 17
proc pie {} {return [expr acos(-1)]}
console show
console eval {.console config -bg palegreen}
console eval {.console config -font {fixed 20 bold}}
console eval {wm geometry . 40x20}
# invoking TCLLIB math::numtheory
proc isprimex x {expr {$x>1 && ![regexp {^(oo+?)\1+$} [string repeat o $x]]}}
# list_twin_primes proc under test, list_twin_primes and isprime procs are recursion limited
proc list_twin_primesx { aa bb cc} { for {set i $aa} {$i<=$bb} {incr i $cc} { if {[isprime $i] && [isprime [+ $i $cc ]] } {lappend boo $i [+ $i $cc ] } } ; return $boo}
proc list_twin_primes { aa bb cc} { for {set i $aa} {$i<=$bb} {incr i 1} { if {[isprime $i] && [isprime [+ $i $cc ] ] } { lappend boo $i [+ $i $cc ] } } ; return $boo}
# aa is start number, bb is upper limit, cc is separator number, usually even 2
# The original Dickson conjecture has separator even numbers 2,4,6 ... ?
# list_twin_primes 0 25 2 returns 3 5 5 7 11 13 17 19
# The sets <13 15> and <15 17> are separated by a even 2,
# but left out of answer.
# Note the 15 is not a prime number and has factors <3 5>.
# The set <13 17> has two primes, but separated by an even 4.
# reference On-Line Encyclopedia of Integer Sequences website
# OEIS A077800 discussed that the twin prime sets <p,p+2> are
# (3, 5), (5, 7), (11, 13), (17, 19),
# (29, 31), (41, 43), (59, 61), (71, 73),
# (101, 103), (107, 109), (137, 139)...
# OEIS A275021 has samples of <p,p+4> and omits pairs of <p,p+2>
# 79, 83, 127, 131, 163, 167, 379, 383, 397, 401, 439, 443,...
# list_twin_primes 75 135 4 returns 79 83 103 107 127 131
# reference On-Line Encyclopedia of Integer Sequences website
# OEIS A023201 has some samples of <p,p+6>
# 5, 7, 11, 13, 17, 23, 31, 37,
# 41, 47, 53, 61, 67, 73, 83, 97, 101
# contains redundant procs for testing
puts "[list_twin_primes 3 25 2 ]"
puts "[list_twin_primes 3 25 4 ]"
puts "[list_twin_primes 3 25 6 ]"Table Results on Twin Primes for 2,4,6,10 Separators
| table | Twin Primes for 2,4,6,10 Separators | printed in | TCL format | |
|---|---|---|---|---|
| result | lower limit | upper limit | separator integer | comment, if any |
| elements in list | lower limit | upper limit | separator integer | comment, if any |
| 3 5 5 7 11 13 17 19 | 3 | 25 | 2 | |
| 3 7 7 11 13 17 19 23 | 3 | 25 | 4 | |
| 5 11 7 13 11 17 13 19 17 23 23 29 | 3 | 25 | 6 | |
| 3 13 7 17 13 23 19 29 | 3 | 25 | 10 |
2021 Newsflash, TCLLIB has twin primes and cousin primes routines in TCLLIB:math ticket pipeline
gold 5/13/2021. See for more hacks on this issue. Gauss Approximate Number of Primes [L26 ]. Monster Prime Predicting Formula. Search on wiki search engine for twin prime Gauss Monster
closer: arjenmarkus AM
Emailed icomment from AM: I used the sample code to create two new procedures:
listPrimePairs listPrimeProgressions
The first proc listPrimePairs returns a list of pairs of primes that differ by a given number and the second proc listPrimeProgressions returns a list of arithmetic progressions of primes that differ by the given number.
Bits and Pieces, Testing One Liner Programs
set strinit “123456789”
proc string_end strin5 { string index $strin5 end}
string_end $strinit
# out 9
proc sea5 bb { set i 2;if {$i < 10} { while {$i < 5} { puts [incr i]}}}
sea 5
# return first character of string
proc string_end5 bb { string index $bb 0 }
# return last character of string
proc string_end5 bb { string index $bb end }
# Enter number num for next above power of 2, John K. Ousterhout, Tcl and the Tk Toolkit
proc near_above_power_of_2 num {set pow 1; while {$pow<$num} {set pow [expr { $pow*2} ]}; return $pow}
# Usage near_above_power_of_2 7 returns 8,
# Usage near_above_power_of_2 9 returns 16,
# Usage near_above_power_of_2 99999999999999 140737488355328
# Enter number num for next below power of 2, John K. Ousterhout, Tcl and the Tk Toolkit
proc near_below_power_of_2 num {set pow 1; while {$pow< [expr {$num - 1}] } {set pow [expr { $pow*2} ]}; return [expr { $pow*.5} ]}
# Usage near_below_power_of_2 7 returns 4. Fortran Like "Call" Procedure
gold Here are one line procedures for fortran like "call" in TCL, mostly altered proc from LV on Wiki page of Salt and Sugar. See also Call Procedure Like Fortran Example
console show
proc pie {} {expr acos(-1)} # AMG
proc writer {args } { puts $args }
proc call {args} {uplevel catch [list $args]}
call writer "jack" "&" "jill"
call writer jack & jill went up the hill with [pie]Circle Area and Law of Cosines
gold Here are some one line procedures for circle area and law of cosines. See tcl::mathfunc cos pi constants Functions ::math::constants::constants and ::math::fibonacci are available in the TCLLIB. Most of these one liner programs were revamped on the advice of AMG. Most one liners should be pastable into the TCL console for further testing.
console show
proc pi {} {expr {acos(-1)}} # AMG
# proc pi from AMG see below
proc degtoradiansconst {} { expr {180./ [pi] }}
proc degz {} { expr {180./ [pi] }}
proc degx {aa} { expr { degz *acos($aa)}}
proc inrad {a b c} { expr {(sqrt(($a+$b+$c)*($a+$b-$c)*($a-$b+$c)*($b+$c-$a)))/(2.*($a+$b+$c))}}
proc circlediameter {radius} { expr { 2.* $radius }}
proc circlearea {radius} { expr { [pi] *($radius**2)}}
proc circlecircumference {radius} { expr {2.* [pi] *$radius }}
proc spherediameter {radius} { expr { 2.* $radius }}
proc spherevolume {radius} { expr { (4./3.)* [pi] *($radius**3)}}
proc spheresurface {radius} { expr { 4.* [pi] *($radius**3)}}
proc cubevolume {aa} { expr { 1.*$aa*$aa*$aa }}
proc squarearea {aa} { expr { 1.*$aa*$aa }}
proc ellipsoidvolume {aa bb cc} { expr { 1.*(4./3.)* [pi] *$aa*$bb*$cc }}
proc ellipsearea1 { aa bb } { expr { 1.* [pi] *$aa*$bb }}
proc ellipseperimeterx {aa bb} { set tt [ expr { ($aa*$aa+$bb*$bb)/2.}];return [ expr { 2.*[pi]*sqrt($tt)} ] }
proc spherevolumex {aa } { expr { 1.*(4./3.)* [pi] *$aa*$aa*$aa }}
proc spheroidvolumex {aa cc } { expr { 1.*(4./3.)* [pi] *$aa*$aa*$cc }}
proc torusvolumex {aa bb } { expr {(1./4.) * [pi] * [pi] * ($aa + $bb) * ($aa - $bb)*2.}}
proc torussurfacex {aa bb } { expr { [pi] * [pi] * ($aa*$aa - $bb*$bb)}}
proc conesurfacex {aa rr } { expr { [pi] *$rr*$aa}}
proc cylindersurfacesidex {aa rr } { expr {2.* [pi] *$rr*$aa}}
proc cylinderwholesurfacesidex {aa rr } { expr {2.* [pi] *$rr*$aa +2.* [pi] *$rr*$rr}}
proc cylindervolumesidex {aa rr } { expr { [pi] *$rr*$rr*$aa}}
proc conevolumex {aa rr } { expr { (1./3.)* [pi] *$rr*$rr*$aa}}
proc pyramidvolumex {aa bb cc } { expr {(1./3.)*$aa*$bb*$cc }}
proc rectangularprismvolumex {aa bb cc } { expr { $aa*$bb*$cc }}
proc triangularprismvolumex {aa bb cc } { expr { $aa*$bb*$cc*.5 }}
proc polygonperimeterx {aa bb } { expr { $aa*$bb}}
proc rectangleperimeterx {aa bb } { expr {2.*( $aa+$bb)}}
proc parallelogramperimeterx {aa bb } { expr {2.*( $aa+$bb)}}
proc triangleperimeterx {aa bb cc} { expr { $aa+$bb+$cc }}
proc triangletrapezoidx {aa bb cc} { expr { $aa*($bb+$cc)*(1./2.)}}
# law of cosines, aa bb cc are three sides of right triangle, here ordered
# as aa small side , bb middle side, cc largest side.
# inrad is radius of cirle inscribed in right triangle,
# use sides as inrad aa bb cc
proc anglecosa { aa bb cc } { expr {($bb*$bb+$cc*$cc-$aa*$aa)/(2.*$bb*$cc)}}
proc anglecosb { aa bb cc } { expr {($cc*$cc+$aa*$aa-$bb*$bb)/(2.*$aa*$cc)}}
proc anglecosc { aa bb cc } { expr {($aa*$aa+$bb*$bb-$cc*$cc)/(2.*$aa*$bb)}}
# with examples
# for radius of 1
# circlediameter 1
# circlearea 1
# circlecircumference 1
# spherediameter 1
# spherevolume 1
# spheresurface 1
# inrad 3 4 5
# anglecosa 3 4 5
# anglecosb 3 4 5
# anglecosc 3 4 5
# following include redundant TCL one liner procedures for sqrt of sum of squares
# sqrt of sum of squares and diagonal using expr
proc diagonal_1 {aa bb} { expr { sqrt($aa * $aa + $bb * $bb)}}
# Usage diagonal 1 1 s 1.4142135623730951
# diagonal using math ops
proc diagonal_2 {aa bb} {[sqrt [+ [* $aa $aa] [* $bb $bb] ] ]}
# Usage diagonal_2 1 1 returns 1.4142135623730951
# diagonal using math hypot function
proc diagonal_3{aa bb} {[ hypot $aa $bb ]}
# Usage diagonal_3 1 1 returns 1.4142135623730951
# time one liners, but sticking >> [ time { set qq [ diagonal_1 1 1 ] } ]
proc diagonal_1x {aa bb} { [ time [sqrt [+ [* $aa $aa] [* $bb $bb] ] ]]}
proc koch_snowflake_perimeter { side1 iteration } {return [ expr { 3.*$side1*((4./3.)**$iteration)}] } gold 8/20/2021. fractal geometry updates [L27 ]
proc koch_snowflake_perimeter { side1 iteration } {return [ expr { 3.*$side1*((4./3.)**$iteration)}] }
# Usage using set answer
set answer3 [ koch_snowflake_perimeter 1. 5. ]
proc area_eq_triangle { length } { return [ expr { ($length*$length*sqrt(3.))/4.} ] }
# area_eq_triangle has to be initial triangle of length XX, if not equilateral triangle of 1.
# Usage using set answer
set area_eq_triangle [ area_eq_triangle 1. ]
proc koch_snowflake_nth { iteration area_eq_triangle } {return [ expr { ($area_eq_triangle / 5.) * (8.-3.*(4./9.)**$iteration)}]}
# Usage using set answer
set area_eq_triangle [ area_eq_triangle 2. ] # answer = 1.7320508075688772
set answer2 [ koch_snowflake_nth 1 $area_eq_triangle ] # answer2 = 2.3094010767585034"Chance of" and rand() Conditions
gold Here are some one liners for "chance of" conditions. The "chance of" procedures make use of the random function and do not return the same answer everytime. The random function was used in the Random Walk Equation Slot Calculator Example. Chances of weather and other conditionals were used in Game Kingdom of Strategy. Weather and other conditionals are especially important in games and military strategy. See also rand random tcl::mathfunc.
# suggest maintain spaces near expr statement
proc emmy aa {expr {rand()<.9? 1 : 0 }}
proc emmy2 aa { if { [ expr { rand() } ] <= .90 } {return 1 }}
if { [ expr { rand() } ] <= .90 } {set immigrantyear 1 }
# try if { { rand() } <= .90 } {set immigrantyear 1 } #; should work
proc plaguex aa { expr {rand()<.15? 1 : 0 }}
if { [ expr { rand() } ] <= .15 } {set plaguethisyear 1 }
# try if { { rand() } <= .15 } {set plaguethisyear 1 } #; should work
# There is a 15 percent chance of plague this year
# with random casualities up to 10 percent of population.
proc plaguelossx aa {expr {rand()<.15? int($aa*.1*rand()) : 0 }}
proc ratx aa {expr {rand()<.41? 1 : 0 }}
if { [ expr { rand() } ] <= .41 } {set ratinfestthisyear 1 }
# try if { { rand() } <= .41 } {set ratinfestthisyear 1 } #; should work
set liters 1000.; set sumerians 2000.
set ratliters [ expr { $liters*.1*rand() } ]
set ratliters [ expr { int($ratliters) } ]
set sumeriansstarved [ expr { $sumerians*.02*rand() } ]
set sumeriansgain aa {expr {rand()<.15? $aa*.1*rand() : 0 }}
set sumeriansgain [ expr { $sumerians * .10 * rand() } ]
set sumeriansgain [ expr { int($sumeriansgain) } ]
set sumerians [ expr { $sumerians + $sumeriansgain } ]Linear Interpolation, logic tests for even - odd of positive numbers
Here is a one line procedure for linear interpolation. Where (xx1,yy1) and (xx3,yy3) are picked from a line. An intermediate point is picked at xx2. Solution is for yy2. This code is placed here as one line program examples. This page is not a replacement for the current TCL core and TCLLIB with much improvement since TCL4. See better routines, current methods, and whole library on high quality linear interpolation in TCLLIB distribution. No safety nets here for negative and real numbers. Refer to switch & Tcl Tutorial Lesson 6 Math Sugar [L28 ] [L29 ]
# logic tests for even, odd, positive, negative, conditions of positive numbers
# uses logic inside expr , if positive return 1, if not positive return 0
proc isPositive x {return [ expr {$x>0}]} # Richard Suchenwirth RS idea in Math Sugar
# uses logic inside expr, if negative return 1, if not negative return 0
proc isNegative x { return [ expr {$x<0}]} # Richard Suchenwirth RS idea from wiki: Math Sugar
# idea by Michael Barth
# No error traps or safety nets here for negative and real numbers.
# conditional proc IsOdd, if N odd, return 1, if N not odd, return 0.
proc IsOdd { N } { return [ expr {$N % 2} ] }
# Usage
IsOdd 5 # returns 1
# conditional proc IsEven, if N even, return 1. If N not even return 0.
proc IsEven { N } { return [ expr { ( $N + 1 ) % 2} ] }
IsEven 4 # returns 1
# linear interpolation
# See better routines on high quality linear interpolation in TCLLIB distribution.
# points (xx1,yy1) and (xx3,yy3) are picked from a line.
# An intermediate point is picked at xx2. Solution is for yy2.
proc interlinear {xx1 xx2 xx3 yy1 yy3} { return [expr {((($xx2-$xx1)*($yy3-$yy1))/($xx3-$xx1))+ $yy1 }]}Decimal Equivalents to some Babylonian Math Tables
gold Following one liners are decimal equivalents to some Babylonian math tables, using mathop here from Babylonian Cubic Equation Problem and eTCL demo example calculator, numerical analysis. Mostly, these one liners programs are returning lists of numbers.
# following one liners are decimal equivalent to some Babylonian tables
# possible cubic problem instances include separate tables for cubes n*n*n and quasi_cubes
# quasi_cube n*n*(n-1), quasi_cube n*(n + 1)*(n + 2), quasi_cube n*n*(n + 1), quasi_square n*(n+1)
# list_integers is list of positive integers, 1 2 3 4 ... n
proc list_integers { aa bb} { for {set i 1} {$i<=$bb} {incr i} {lappend boo [* 1. $i ] [* $i 1.]};return $boo}
# usage, list_integers 1 10
# 1.0 1.0 2.0 2.0 3.0 3.0 4.0 4.0 5.0 5.0 6.0 6.0 7.0 7.0 8.0 8.0 9.0 9.0 10.0 10.0
# list_reciprocals is list of 1/1 +1/2 1/3 1/4 ... 1/n
proc list_reciprocals { aa bb} { for {set i 1} {$i<=$bb} {incr i} {lappend boo [* 1. $i ] [/ 1. $i ]};return $boo}
# usage, list_reciprocals 1 10
# 1.0 1.0 2.0 0.5 3.0 0.333 4.0 0.25 5.0 0.2 6.0 0.166 7.0 0.142 8.0 0.125 9.0 0.11 10.0 0.1
# list_squares is list of integer squares,
proc list_squares { aa bb} { for {set i 1} {$i<=$bb} {incr i} {lappend boo [* 1. $i ] [* $i $i ]};return $boo}
# usage, list_squares 1 10
# 1.0 1 2.0 4 3.0 9 4.0 16 5.0 25 6.0 36 7.0 49 8.0 64 9.0 81 10.0 100
# quasi_cube2 is n*(n)*(n-1)
proc list_quasi_cube2 { aa bb} { for {set i 1} {$i<=$bb} {incr i} {lappend boo [* 1. $i ] [* $i $i [- $i 1]]};return $boo}
# usage, list_quasi_cube2 1 10
# 1.0 0 2.0 4 3.0 18 4.0 48 5.0 100 6.0 180 7.0 294 8.0 448 9.0 648 10.0 900
# quasi_cube3 is n*(n+1)*(n+2)
proc list_quasi_cube3 { aa bb} { for {set i 1} {$i<=$bb} {incr i} {lappend boo [* 1. $i ] [* $i [+ $i 1] [+ $i 2]]};return $boo}
# usage list_quasi_cube3 1 10
# 1.0 6 2.0 24 3.0 60 4.0 120 5.0 210 6.0 336 7.0 504 8.0 720 9.0 990 10.0 1320
# quasi_cube4 is n*(n)*(n+1)
proc list_quasi_cube4 { aa bb} { for {set i 1} {$i<=$bb} {incr i} {lappend boo [* 1. $i ] [* $i $i [+ $i 1]]};return $boo}
# usage, list_quasi_cube4 1 10
# 1.0 2 2.0 12 3.0 36 4.0 80 5.0 150 6.0 252 7.0 392 8.0 576 9.0 810 10.0 1100
# quasi_square2 is n*(n+1),
proc list_quasi_square2 { aa bb} { for {set i 1} {$i<=$bb} {incr i} {lappend boo [* 1. $i ] [* $i [+ $i 1]]};return $boo}
# usage, list_quasi_square2 1 10
# 1.0 2 2.0 6 3.0 12 4.0 20 5.0 30 6.0 42 7.0 56 8.0 72 9.0 90 10.0 110
# list_sum_integers
proc list_sum_integers { aa bb} { for {set i 1} {$i<=$bb} {incr i} {lappend boo [* 1. $i ] [/ [* $i [+ $i 1] ] 2. ]};return $boo}
# usage, list_sum_integers 1 10
# 1.0 1.0 2.0 3.0 3.0 6.0 4.0 10.0 5.0 15.0 6.0 21.0 7.0 28.0 8.0 36.0 9.0 45.0 10.0 55.0
# list_sum_squares
proc list_sum_squares { aa bb} { for {set i 1} {$i<=$bb} {incr i} {lappend boo [* 1. $i ] [/ [* $i [+ $i 1.] [+ [* $i 2.] 1.]] 6.]};return $boo}
# usage list_sum_squares 1 10
# 1.0 1.0 2.0 5.0 3.0 14.0 4.0 30.0 5.0 55.0 6.0 91.0 7.0 140.0 8.0 204.0 9.0 285.0 10.0 385.0Some fragmented Babylonian tables known as n*n*(n+1) tables were used in solving some cubic equations, ref Joran Friberg. The equations were of the form n*n*(b*n+1) = c. The eTCL calculator could generate the expected tables of n*n*(n+1). Other Babylonian tables known as n*(n + 1)*(n + 2) and n*n*(n – 1) tables have been identified, but no abundant use has been cited from the known Babylonian math problems. Although not clear, tables of the n*(n + 1) might have existed. From modern theory, n · (n + 1)/2 = sum of integers (1,2,3,4...) and n*(n + 1)*(n + 2) /6 = sum of squares (1,4,9....). Possibly, the Seleucid math problem used an n*(n + 1)*(n + 2) table. Possibly, the tables for n*(n + 1)*(n + 2) and n*n*(n – 1) could have been used for cubic equations. The Seleucid method for sum of squares can be factored for sum of integers term and can be restated as a quasi_cube, ((1/3)(1+2 *n) ) * ( n(n+1)/2.) = (1/6)* n(n+1)(2n+1) = (1/6)*quasi_cube term. Another possible form for the quasi_cube (1/6)* n(n+1)(2n+1) with 2 factored out is expression 2*(1/6)* n(n+1)(n+(1/2)) . Problems for sum of squares and sum of rectangles go far back through the Selucid and Old Babylonian math, although Old Babylonian math may not demonstrate complete knowledge. At least in referring to TCL procs, the Babylonian table known as n*(n + 1)*(n + 2) is not that far from the sum of squares and triangular numbers as n*(n + 1)*(n + 2)/6.
# Auxiliary math series used along side B. math problems.
# B. math used <x-1/x> as initial square root estimate or square root component
# in some square root problems and B. triplet algorithms, ref Plimpton 322.
proc list_bab_sqrt { aa bb} { for {set i 1} {$i<=$bb} {incr i} {lappend boo [- [* 1. $i] [/ 1. $i]] };$boo}
# Usage list_bab_sqrt 0 10, bb is upper limit, aa is lower limit as set i $aa
# output 0.0 1.5 2.666 3.75 4.8 5.83 ...
proc list_sqrt { aa bb} { for {set i 1} {$i<=$bb} {incr i} {lappend boo [sqrt $i ] };$boo}
# Usage list_sqrt 0 10, bb is upper limit, aa is lower limit as set i $aa
# output 1.0 1.414 1.732 2.0 2.236 2.449 ... standard square roots
# B. math used <x+1/x> as initial increment estimate or square root component in some B. triplet algorithms, ref Plimpton 322.
proc list_bab_math { aa bb} { for {set i 1} {$i<=$bb} {incr i} {lappend boo [+ [* 1. $i] [/ 1. $i]] };$boo}
proc list_bab_reciprocal_formula2 { aa bb} { for {set i 1} {$i<=$bb} {incr i} {lappend boo [* .5 [- [* 1. $i] [/ 1. $i]]] };$boo}
# Usage list_reciprocal_formula2 0 10, bb is upper limit, aa is lower limit as set i $aa
# output 0.0 0.75 1.33 1.875 2.4 2.916 3.42857 ...
proc list_bab_reciprocal_formula3 { aa bb} { for {set i 1} {$i<=$bb} {incr i} {lappend boo [* .5 [+ [* 1. $i] [/ 1. $i]]] };$boo}
# Usage list_reciprocal_formula3 0 10, bb is upper limit, aa is lower limit as set i $aa
# output 1.0 1.25 1.66 2.125 2.6 3.083 ...Triangular Numbers
Functions ::math::constants::constants, ::math::random, math::combinatorics, math::specialfunctions, and ::math::fibonacci are available in the TCLLIB. Also see Triangular Numbers [L30 ]
# triangular_number_ref_quasi_square3 is n*(n+1)/2,
proc triangular_numbers_ref_quasi_square3 { aa bb} { for {set i 1} {$i<=$bb} {incr i} {lappend boo [* 1. $i ] [* $i [+ $i 1] .5 ]};return $boo}
# usage, list_quasi_square2 1 10
# 1.0 2 2.0 6 3.0 12 4.0 20 5.0 30 6.0 42 7.0 56 8.0 72 9.0 90 10.0 110
# usage < triangular_numbers_ref_quasi_square3 1 10 >
# formula for triangular number is n(n+1)/2
proc triangular_number_2 {nn} { return [ expr { $nn*($nn+1.)/2. } ]}
proc tri_triangular_number n { [* [* $n [+ $n 1] ] .5 ] } # good
# sum triangular number TNS = N*(N+1)*(N+2)/6
proc sum_triangular_number {nn} { return [ expr { $nn*($nn+1.)*($nn+2.)/6. } ]}
# omitting return and expr words for brevity
# switching to math ops rather than expr
proc tri_sum_triangular_number n { [/ [* $n [+ $n 1] [+ $n 2] ] 6 ] } # good
# usage < sum_triangular_number 2 >
# sum_triangular_number series 1,4,10,20,35,56,
# OEIS A000217 reports triangular numbers as
# 1, 3, 6, 10, 15, 21, 28, 36, 45, 55 ... ?
# OEIS A000292 reports Tetrahedral (or triangular pyramidal) numbers:
# a(n) = C(n+2,3) = n*(n+1)*(n+2)/6.
# 0, 1, 4, 10, 20, 35, 56, 84, 120, 165 ... ?
# some formulas pub. Elie de Joncourt, 1762, Netherlands
# triangular number TN = N*(N+1)/2
# alternate formula TN = 0.5*N*(N+1)
# check >> sum of consecutive TN numbers are squares
# TN <aa> + TN <aa+1> = square
# Joncourt used TN to calculate square roots and cube roots
# Joncourt used mult. aa * bb = <(aa+bb)**2 -aa**2 -bb**2>/2
# term <(aa+bb)**2 -aa**2 -bb**2> is twice answer
# binomial theorem >> a*b = 0.5*{(a+b)**2 -a**2-b**2}.
# James Glaisher pub. TN formula from 1889
# TN multiplication aa * bb = TN <aa-1> + TN <bb> - TN <aa-bb-1>
# undefined region and products between -1. > N < 1.
# James Glaisher discussed TN and Quarter Square variants
# Quarter Square >> a*b = <(a + b)**2 − (a − b)**2> * .25
# The TCL procedures use base_10 in calculator.
# For comparison, TCL code may include redundant paths & formulas.
# alternate one liners programs for lists of working series
# based on notes of [antirez] in [Tcl the Misunderstood]
proc working_list_squares {} {lmap i {1 2 3 4 5 6 7 8 9} { expr { $i*$i} }}
# Usage working_list_squares returns 1 4 9 16 25 36 49 64 81
proc working_list_triangular1 {} {lmap i {1 2 3 4 5 6 7 8 9} { expr { $i*($i+1)/2} }}
# Usage working_list_triangular returns 1 3 6 10 15 21 28 36 45
# See benefits of using args in following?
proc working_list_triangular {args} {lmap i $args { expr { $i*($i+1)/2} }}
# Usage working_list_triangular 1 2 3 returns 1 3 6
# Usage working_list_triangular 1 2 3 4 5 6 7 8 9 returns
proc working_list_sum_triangular {args} {lmap i $args { expr { $i*($i+1)*($i+2)/6} }}
# Usage working_list_sum_triangular 1 2 3 4 5 6 7 8 9
# returns 1 4 10 20 35 56 84 120 165
# Usage time { working_list_sum_triangular 1 2 3 4 5 6 7 8 9} 5000
# returns 2.847 microseconds per iteration, fairly fastElectrical Procs
# formula for two parallel resistors of resistance aa and bb ohms.
proc parresistor2 {aa bb } { return [ expr (($aa * $bb )/ ($aa + $bb))]}
# usage: set resistor [ parresistor 100 100 ];answer is 50.
# formula for three parallel resistors of resistance aa, bb, and cc ohms.
proc parresistor {aa bb cc } { return [ expr (($aa * $bb * $cc)/ ($aa*$bb+$aa*$cc+$bb*$cc))]}
# usage: set resistor [ parresistor 100 100 100 ];answer is 33
# formula for fet transistor of volttage 0.009 volts and resistance bb ohms.
proc fetvolts {aa bb } { return [ expr ($aa * $bb )]}
# fet transistor load usage: set fetvolts [ .009 2500 ];answer is 22.5
# formula for fet transistor of volttage 0.009 volts, resistance bb ohms, cc and dd volts.
proc fetdrainvolts {aa bb cc dd } { return [ expr ($aa * $bb + $cc + $dd)]}
# fet transistor usage: set fetdrainvolts [ .009 2500 7 5 ];answer is 34.5
# thin film resistor of dimension aa length and ww width, and sheet resistance cc
proc thinfilmresistor {aa ww cc } { return [ expr (($aa * $cc)/ ($ww*1.))]}
# usage ;thinfilmresistor of length 0.8 cm, width 0.2 cm, and sheet resistance of 150 ohms
# set resistance2 [ thinfilmresistor {.8 .2 100 } ] # answer is 600 ohms
# efficiency and output of electric motor with one horsepower for 746 watts.
proc electrichorsepower {aa bb cc } { return [ expr (($aa * $bb * $cc)* (1./746.))]}# horsepower
# efficiency as 0.8 no_units, voltage as 25 volts, and input current as 10 amps
# The scale factor would be (1./746.) horsepower per watt.
# usage:append details " [ electrichorsepower .8 25 10 ] " # answer is 0.268 horsepower
# formula for cascaded efficiency for n1 *n2 * n3
proc cascadedefficiency {aa bb cc } { return [ expr (($aa * $bb * $cc)* (100./1.))]}#
# example for n1 = 85 percent, n2 equals 90 percent,and n3 equals 73 percent and scale factor 100./1.
# set example_problem [ cascadedefficiency .85 .90 .73 ] #answer is 56 percent.Age of the Earth from Lord Kelvin, history of science
gold Here is the one liner program approach to the age of the earth. These calculations of Lord Kelvin are mainly of historic interest and have been superseded by modern theory.
# Lord Kelvin calculated the age of the earth by approximating the cooling of an molten iron sphere.
# heating of radioactive elements in earth's crust was not considered.
# following assumptions crust thermal defusivity $cc is 1.5E-6 meters/sec*sec,
# As a alternate defusivity estimate, Sandstone is about 1.1E-6 meters/sec*sec.
# alpha $dd is 0.04 degrees centigrade per meter
# initial temperature $aa was 2500 centgrade degrees ,
# final temperature $bb was near zero degrees centigrade.$ee was number seconds in year was 3156000 seconds.
proc kelvinearthtempage {aa bb cc dd ee} { return [ expr (($aa - $bb)*($aa - $bb)/ ( $cc * [pi]* $dd* $dd*$ee))]}
# Kevin estimated a low and high age estimate of 25 million years and 100 million years, respectively.
# usage: low estimate: set age_of_earth " [ kelvinearthtempage 2500 .1 .0000015 .04 31536000. ] "# answer 26 million years
# usage: high estimate could be: set age_of_earth " [ kelvinearthtempage 5100 .1 .0000015 .04 31536000. ] "# answer 110 million yearsHistorical Kelvin Earth Cooling and eTCL Slot Calculator Demo Example , numerical analysis edit
One Liner Approach to the Fibonaci series
gold Here is the one liner approach to the Fibonaci series. However, the algorithms are limited to positive numbers only. Performance may suffer degradation due to lengthy calls and limits on the number of procedure recursion calls. See Fibonacci numbers, Additional math functions, and math::constants. Functions ::math::constants::constants and ::math::fibonacci are available in the TCLLIB.
proc fib {n} { if {$n < 2} then {expr {$n}} else {expr {[fib [expr {$n-1}]]+[fib [expr {$n-2}]]} }}
# Usage: $x.text insert 1.0 " goo [ fib 8 ] " or answewr is 21
# Usage set xat [fib 10] or answwer is 55
# Usage set zat [fib 11] or answer is 89
# Now, lets define and pseudocode for formula of golden section as
# fib N+1 / fib Nth and substitute fib 11 / fib 10
# for rough estimate of golden section: set gat [ expr { ($zat*1.) / ($xat*1.) } ]
# answer was 1.6181818 whereas the exact value was (1+sqrt(5))/2 (approx 1.6180339887)
# from the procedure with the exact formula.
proc gm {args} { expr {.5*(1+sqrt(5))} $args}
# Usage on golden mean, [gm] returns 1.618033988749895
# Usage [gm /4] returns 0.4045084971874737
# Usage [gm /8.] returns "0.20225424859373686"
# time { gm /8. } 5000 returns 4.2298 microseconds per iteration
# Usage to generate rectangle of golden proportions,
# rectangle length equals golden mean constant * width
set width 125 ; set length {* $width [gm] } :# for example
set length [gm *$width ] :# for example returns 202.254
# Now, lets define and pseudocode an error formula either by
# [ expr { 1 -(estimated)/( ideal & exact ) } ] or
# if negative and not greater than one,
# set error as [ expr ( ideal & exact ) / (estimated) -1. ]
set dat [ expr { (( ($zat*1.) / ($xat*1.)) / [ gm *1. ] -1.) } ]or 0.0000913
# Meaning the ratio of the 10 and 11th terms approach the limit by 0.0000913 error AMG: Here's another implementation, using expr's ?: operator instead of if:
proc fib {n} {expr {$n < 2 ? $n : [fib [expr {$n - 1}]] + [fib [expr {$n - 2}]]}} # AMGgold Here is mathops & mathlib follow-on to the one liner approach to the Fibonaci series, using Binet formula for fibonacci (N). See Fibonacci numbers. The library call is ::math::Fibonacci (N).
proc listfib { aa bb} { for {set i 1} {$i<=$bb} {incr i} {lappend booboo [ int [ binet $i] ] };return $booboo}
proc binet { n} {set n [int $n ]; return [int [* [/ 1 [sqrt 5]] [- [** [/ [+ 1 [sqrt 5]] 2 ] $n ] [** [/ [- 1 [sqrt 5]] 2 ] $n ] ] ] ] }
# Usage, set binet1 [ binet 8] # answer 21, removing int's will return real numbers
# Usage, set fibno [ listfib 1 8 ], answer 1 1 2 3 5 8 13 21
proc fibonacci_approx_for_large_N {n} { set phi [/ [+ 1 [sqrt 5]] 2 ] ; return [round [/ [** $phi $n ] [sqrt 5 ]]] } # test only, not sure for all N
listfib 1 20
1 1 2 3 5 8 13 21 34 55 89 144 233 377 610 987 1597 2584 4181 6765Proc Titles into Lists
# wish to grab title of TCL procs into lists
# TCL code into flowchart diagram.
# Can one break on the braces?
# need to get rid of braces in print out
string map {\{ "" \} ""} $item # from Abel Vian, TCL Club
proc unbrace_string {item } {string map {\{ "" \} ""} $item }
# hopefully works without return statement
# Usage unbrace_string {REM {WISH} TO USE EXPR MATH}
# returns REM {WISH} TO USE EXPR MATH as a stringAdvanced Topics, Dependent on TCLLIB Math library
# following proc session invoke TCLLIB math & math::trig library
proc pyramid_d {hh bb} { [ acotand [expr (.5*$bb/$hh) ]] }
proc pyra_d {hh bb} { [ acotand [* .5 [/ $bb $hh] ]] }
# pyramid_degrees 57.692 106.346 answer 47.334157521261254
# seked = (7 * .5 * 360 cubits) / 250 cubits = 5.04 decimal palms
proc seked_d {hh bb} { [/ [* 7. .5 $bb ] $hh ] }
# usage seked 250. 360. equals 5.04
# integral of ramp function (2 * $x) over interval of 0 to 1.
proc ramp2 {} { [::math::calculus::integralExpr 0 1 100 {2. * $x * 1.}]}
# ramp2 # returns 1.0
# TCLLIB integration of expr expression in x
# of OEIS formula for pi, ref notes on sequence A003881
proc pie_tcllib {} {set return [::math::calculus::integralExpr 0 100 10000 {(4.* $x)/($x**4 + 1)}]}
# Usage pie_tcllib -> 3.1413926535904273
# set return is old fashioned didactic, for brevity may omit set return
proc pie_pie {} {set return [::math::calculus::integralExpr -100000 100000 1000000 {(1.)/($x*$x + 1.)}]}
# Usage pie_pie # -> 3.1415726535896074
# integrate f(x) for pi from minus inf to plus inf, but slowly converges
# set return is old fashioned didactic , for brevity may omit set return
proc pi {} {expr acos(-1)} # AMG
expr sqrt([pi]) # -> 1.7724538509055159 sqrt of pi
proc pie_sqrt {} { [::math::calculus::integralExpr -100000 100000 1000000 { exp (-$x * $x )}]}
# Usage pie_sqrt # -> 1.772453850905516
# integrate f(x) for pi sqrt from minus inf to plus inf, but slowly converges
proc pie_si {} { [::math::calculus::integralExpr -100000 100000 1000000 { sin($x) / $x }]}
# pie_si # returns -> 3.1416126408100333 ... -> pi
# integrate f(x) for pi si from minus inf to plus inf, but slowly converges
# Aristotle constant 22./7. > pi, expr { 22./7. - [pi] } -> 0.0012644
proc picc {} { [::math::calculus::integralExpr 0 1. 100 { $x**4 * (( 1. - $x )**4) / (1. + $x**2) }]}
# Usage picc -> 0.0012644892673427967
# proof that Aristotles 22./7. slightly greater than pi
# obtain area of unit circle, radius = 1
# x**2 + y**2 = r**2, 2* half circle evaled in $x
proc pill {} { [::math::calculus::integralExpr -1 1 10000 { 2.* sqrt(1. - $x * $x )}]}
# Usage pill # return -> 3.1415921943382195
# accuracy proportionl to number of points integrated
# try 100 points rather than
# 10000 points of demo, 100 points -> 3.141133205339226
# end TCLLIBLooking for methods to transform other formulas and known functions? See Symbolic Differentiation of known functions math::calculus::symdiff , pade rational number approximations, and horner expressions.Evaluating polynomial functions & [L31 ] & [L32 ]
# commands and procs below should should be pastable into TCL easy eye Console
package require math::calculus
namespace import math::calculus::*
proc pi {} {expr acos(-1)} # AMG returns 3.141592653589793
symdiff {acos($x)} x # symbolic differentiation into expr expression
(-1.0 / sqrt((1.0 - ($x * $x))))
proc piexx {} { [::math::calculus::integralExpr -1 1 1000 { 2.* sqrt(1. - $x * $x )}]}
# Usage piexx -> 3.1415781302139947
# fpoolwing variant from changed limits
proc pied {} { [::math::calculus::integralExpr 0 1 10000 { 4.*( sqrt((1.0 - ($x * $x))))}]}
# Usage pied -> 3.141592491220191
proc pixx {} { [::math::calculus::integralExpr 0 1 10000 { (1.0 / (1.0 + ($x * $x)))}]}
# Usage pixx -> 0.7853981633974438 # returns pi/4 Maximum numeric value in list from max
# start TCLLIB Dependency here in Advanced topics
# Find a Maximum numeric value in list from max on TCL WIKI
# maybe overkill on setup requirements, but setup is tricky on Windows10 here
# This is a wiki example anyway, cut and paste what works on your machine.
package require Tcl 8.6
package require math::numtheory
namespace path {::tcl::mathop ::tcl::mathfunc math::numtheory }
set tcl_precision 17
# Found routine for maximum numeric values in list
# suggest control maximum values with index
# for 4 or 5 maximum numeric values in output.
set values_list [ list 1 2 3 4 5 10 6 7 8 9 }
set maximum_values_list [ ::tcl::mathfunc::max {*}$values_list ]
# returns 10
# end TCLLIB Dependency here Simple Error as Percentage
gold Here is one liner procedure developing simple error as percentage error . There are one liner procedures for various error function approximations in One Liners Programs Pie in the Sky, though "not ready for the mars shot" and dependent on helper procs. Functions ::math::special::erf and ::math::special::erfc are available in the TCCLIB math library. See TCLLIB. Whether in TCL, Javascript, or Fortran77, this percentage error subroutine is one of the most useful algorithms on this page (to me).
# proc errorx always returns a positive error.
# Normally assume $aa is human estimate,
# assume $bb is divinely exact or textbook standard estimate.
proc errorx {aa bb} {expr { $aa > $bb ? (($aa*1.)/$bb -1.)*100. : (($bb*1.)/$aa -1.)*100.}}
# Usage errorx 3.1 3.14 returns 1.2903 in positive percent
# Usage errorx 3.14 3.1 returns 1.2903 in positive percent
# Usage errorx 3.03 3.141592 returns 3.6829 in positive percentgold 6/19/2021 update
# Usage from one line programs in Searching Babylonian triplets
# Usage comparing accuracy of Heron_method and pythagorean_theorem for opposite side
# opposite side (height) = expr { .5 *(2-(.5/2.)) } = 0.875
set heron_method [ expr { .5 *(2-(.5/2.)) } = 0.875 ] # returns 0.875
set pythagorean_theorem_height [expr { sqrt (1**2-.5**2) } # returns 0.8660 rnd for opposite side
proc errorx {aa bb} {expr { $aa > $bb ? (($aa*1.)/$bb -1.)*100. : (($bb*1.)/$aa -1.)*100.}}
set percent_error [ errorx 0.875 0.8660] # returns 1 percent error rounded # Usage example of errorx as one liner program
# in finding percentage errors and average of errors.
# The ukullu or inverse slope
# was expr { triangle side $adjacent/ side $opposite }.
# The adjacent side or triangle short side was between
# the triplet 19 = 0.501 and triplet 20 = 0.4875 on Plimpton 322 extension
# setting percent errors of triangle short side .5 between triplet 19 = 0.501
# and triplet20 = 0.4875
set error5 [ errorx .5 0.501 ] # returns 0.2000 percent relative error
set error6 [ errorx .5 0.4875 ] # returns 2.5641 percent relative error
set average_error_on_2 [ expr { ( $error5 + $error6 ) * 0.5 } ]# returns 1.38205 average percent relative error # Use one line errorx proc to estimate percent errors in approximate Elliot Wave Breakpoints
proc errorx {aa bb} {expr { $aa > $bb ? (($aa*1.)/$bb -1.)*100. : (($bb*1.)/$aa -1.)*100.}}
set grc 1.61803398874989484820 # golden ratio constant
set grc .61803398874989484820 # golden ratio conjugate
set wave_1a [ expr { 5./8. } ] # returns 0.625, very rough approximate $grc
set wave_2a [ expr { 8./5. } ] # returns 1.6, very rough approximate $gr
set wave_3a [ { 832040./ 1346269.} ] # returns 0.6180339887496481
set error_1 [ $grc [/ 5. 8. ] # returns 1.127 percent error on very rough approximate $grc
set error_2 [ $grc [/ 987. 1597. ] # returns 2.837e-5 percent error
set error_3 [ $grc [/ 832040. 1346269. ] # returns 3.992e-11 percent error #; Eratosthenes' method to calculate the Earth's circumference has been lost.
#; Original units were greek_stadia which are converted to meters here.
#; 1 greek_stadium (really Egyptian unit) is equal to 157.5 meters
set greek_stadia_length [ expr { 5000.0 * 157.5} ] # returns 787500.0 meters
set earth_circumference [ expr { 360. *787500.0 / 7.2} # returns 39375000.0 meters , convert to 39375. kilometers
set earth_circumference_error [ errorx 40076.0 39375. ] # returns 1.78 percent lowTime on One Liner Programs
See Time Also One Liners Programs Pie in the Sky on timing subroutines.
proc timex2 aa { time {puts Hello} $aa } # [RS]
# Usage timex2 10
# Usage timex2 4 returns Hello Hello Hello Hello 751.75 microseconds per iteration
proc timex2 aa { time {puts Hello} $aa }
timex2 { expr { 4+5 } } 1000 # returns 0.268 microseconds per iteration
timex2 {expr 4+5 } 1000 # returns 0.104 microseconds per iteration
# Need to preserve spaces near expr
time { [ + 4 5 ] } 1000 # should be 0.104 microseconds per iteration
time { [ + 4 5 ] } 1000 # returns 9
set t0 [clock clicks -millisec]; puts [expr { 1+2 ]; puts stderr "[expr {([clock clicks -millisec]-$t0)/1000.}] sec" # RS
time { for {set i 0} {$i<1000} {incr i} { # empty body}} # TCL 8.5 TclCmd Manual
# returns 512 microseconds per iteration on machine here proc timex2 aa { time {puts Hello} $aa } # RS
# output for timex2 4
Hello
Hello
Hello
Hello
751.75 microseconds per iterationAdvanced Topics: Figurate Polynomial Formulas for TCL Procs
Table : Figurate Formulas and TCL Procs Table
| Table Figurate Formulas into TCL Procs | printed in | tcl format | ||
|---|---|---|---|---|
| figurate name | formula in variable n | automatic trial TCL proc ************************ | infinite series | comment, if any |
| oblong numbers | n*(n+1) | proc figurate1 { n } {return [ expr {($n+1) }} | 0, 2, 6, 12, 20, 30, 42, 56, 72, 90, 110, ... | |
| triangular numbers | n*(n+1)/2 | proc figurate1 { n } {return [ expr {($n+1)/2}} | 1 3 6 10 15 21 28... | |
| square numbers | n**2 | proc figurate1 { n } {return [ expr {$n**2}} | 1 4 9 16 25 36 49... | |
| pentagonal numbers | n*(3n-1)/2 | proc figurate1 { n } {return [ expr {(3*$n-1)/2}} | 1 5 12 22 35 51 70... | |
| hexagonal numbers | n*(4n-2)/2 | proc figurate1 { n } {return [ expr {(4*$n-2)/2}} | 1 6 15 28 45 66 91... | |
| heptagonal numbers | n*(5n-3)/2 | proc figurate1 { n } {return [ expr {(5*$n-3)/2}} | 1 7 18 34 55 81 112... | |
| octogonal numbers | n*(3n-2) | proc figurate1 { n } {return [ expr {(3*$n-2)}} | 1 8 21 40 65 96 133... | |
| ********************** | 2D figurate numbers into 3D figurate numbers | ************************ | ||
| triangular numbers | n*(n+1)/2 | proc figurate1 { n } {return [ expr {($n+1)/2}} | 1 3 6 10 15 21... | |
| tetrahedral numbers | n*(n+1)*(n+2)/6 | proc figurate1 { n } {return [ expr {($n+1)*($n+2)/6}} | 1 4 10 20 35 56... | |
| hypertetrahedral numbers | n*(n+1)*(n+2)*(n+3)/24 | proc figurate1 { n } {return [ expr {($n+1)*($n+2)*($n+3)/24}} | 1 5 15 35 70 126... |
from Gnumeric spreadsheet
proc figurate1_oblong { n } {[ return [ expr {($n+1) }]}
proc figurate2_triangular { n } {[ return [ expr {($n+1)/2}]}
proc figurate3_square { n } {[ return [ expr {$n**2}]}
proc figurate4_pentagonal { n } {[ return [ expr {(3*$n-1)/2}]}
proc figurate5_hexagonal { n } {[ return [ expr {(4*$n-2)/2}]}
proc figurate6_heptagonal { n } {[ return [ expr {(5*$n-3)/2}]}
proc figurate7_octogonal { n } {[ return [ expr {(3*$n-2)}]}
# ***** 2D figurate into 3D figurate $numbers ******
proc figurate8_triangular { n } {[ return [ expr {($n+1)/2}]} # duplicate proc for comparison
proc figurate9_tetrahedral { n } {[ return [ expr {($n+1)*($n+2)/6}]}
proc figurate10_hypertetrahedral { n } {[ return [ expr {($n+1)*($n+2)*($n+3)/24}]}2021 Newsflash, TCLLIB has Figurate Polynomial routines and sum of powers Formulas routines in TCLLIB:math ticket pipeline
gold 5/13/2021. filed TCLLIB ticket for same. See for more hacks on these issues.
- Triangular Number Multiplication Study and demo example TCL calculator, numerical analysis
- Playing Recursion V2 >> demo examples for one liners programs
- Primal Screens— Part TwoKWJ
Advanced Topics: Polynomials, Sums of Powers, Symbolic Differentiation & Integration in Tcllib Calculus
# adding extra and redundant spaces in proc expressions
# below for wiki readability
# recommend each proc be math checked by hand on small numbers (2,3,4)
# recommend each proc be checked for small, medium, and large numbers
# in expected range of operation
# one may leave off return commands and unnecessary spaces for brevity
# formula for Sum of Squares is k(2) = n*(n+1)*(2*n+1)/6
proc sum_squares { n } {set res [expr { $n*($n + 1)*(2*$n +1 ) / 6 }]}
# Usage sum_squares 2 -> 5
# check answer expr 2**2 -> 4, 4 + 1 = 5
# Usage sum_squares 1000000 -> 333333833333500000
# formula for Sum of Cubes is k(3) = (n**2)* ((n + 1)**2) / 4
proc sum_cubes { n } {set res [expr { ($n**2)* (($n + 1)**2) / 4 }]}
# Usage sum_cubes 2 -> 9
# check answer expr 2**3 -> 8, 8 + 1 = 9
# Usage sum_cubes 1000000 -> 250000500000250000000000
# formula sum_4th_power k(4) = n* (n + 1)* (2*n + 1 )* ( 3*n**2 + 3*n -1)/30
# using integer arithmetic for the long digit answers
proc sum_4th_power {n} { expr { $n* ($n + 1)* (2*$n + 1 )* (3*$n**2 + 3*$n -1)/30}}
# Usage sum_4th_power 2 -> 17
# check answer expr 2**4 -> 16, 16 + 1 = 17
# Usage sum_4th_power 0 -> 0 # Usage sum_4th_power 1 -> 1
# Usage sum_4th_power 1000 -> 200500333333300
# Usage sum_4th_power 200 -> 64802666660
# Usage sum_4th_power 1000000000
# -> 200000000500000000333333333333333333300000000
# formula sum_5th_power k(5) = n*n* (n+1)* (n+1 )* ( 2*n**2 + 2*n -1)/12
proc sum_5th {n} {return [expr {($n*$n* ($n + 1)*($n + 1 )*(2*($n**2)+2*$n - 1))/12}] }
# internal ? in expr testing for 2 conditions
proc sum_5th_power {n} {expr { $n < 1? 0: $n > 1 ? 1 : ($n*$n* ($n + 1)*($n + 1 )*(2*($n**2)+2*$n - 1))/12}}
# Usage sum_5th_power 0 -> 0 # Usage sum_5th_power 1 -> 1
# Usage sum_5th_power 2 -> 33
# formula sum_6th_power k(6) =( n*(n + 1)*(2*n + 1 )*(3*(n**4)+(6*(n**3))-(3*n) + 1))/42
proc sum_6th {x} {return [expr {( $x*($x + 1)*(2*$x + 1 )*(3*($x**4)+(6*($x**3))-(3*$x) + 1))/42}] }
# Usage sum_6th 2 -> 65
# check answer expr 2**6 = 64, 1 + 64 = 65
# formula sum_7th_power k(7) =( n*n*(n + 1)*(n + 1)*(3*(n**4)+(6*(n**3))-n*n-(4*n) + 2))/24
proc sum_7th {x} {return [expr {( $x*$x*($x + 1)*($x + 1)*(3*($x**4)+(6*($x**3))-$x*$x-(4*$x) + 2))/24}] }
# Usage sum_7th 2 -> 129
# check answer expr 2**7 = 128, 1+128 = 129# adding extra and redundant spaces in expressions below for wiki readability
# recommend each proc be math checked by hand on small numbers (2,3,4)
# recommend each proc be checked for small, medium, and large numbers
# in expected range of operation
# one may leave off return commands and unnecessary spaces
# formula sum_8th_power k(8)=(n/90)*(n+1)*(2*n+1)*(5*n**6+15*n**5+5*n**4-15*n**3-n**2+9*n-3)
proc sum_8th {x} {return [expr {($x / 90)*($x + 1)*(2*$x + 1)*(5*$x**6 + 15*$x**5 + 5*$x**4 - 15*$x**3 - $x**2 + 9*$x - 3)}]}
# Usage sum_8th 2 -> 257 # using integer arithmetic
# check answer expr 2**6 = 256, 1 + 256 = 257 # using integer arithmetic
# Usage sum_8th 1000000 ->
# 111110499995666659999999533338000000222219999999966667 # using integer arithmetic
# 1.111116111117778e+53 # add decimal point on integer term (90.) in proc for floating point
# formula sum_9th_power k(9)= (n**2/20)*(n+1)*(n+1)*(2*n**6+6*n**5+n**4 - 8*n**3+n**2+6*n-3)
proc sum_9th {x} {return [expr {($x**2 / 20.) * ($x + 1)*($x + 1)*(2 * $x**6 + 6*$x**5 + $x**4 - 8*$x**3 + $x**2 + 6*$x - 3)}]}
# Usage sum_9th 2 -> 513 # using integer arithmetic
# check answer expr 2**9 = 512, 1 + 512 = 513
# sum_9th 1000000 -> 1.0000050000075e+59 # proc sum_9th for floating point
# formula sum_10th_power k(10)= (n/66)*(n+1)*(2n+1)*(3*n**8+12*n**7+8*n**6 - 18*n**5-10*n**4+24*n**3+2*n**2-15*n+5)
proc sum_10th {x} {return [expr {($x / 66. )*($x + 1)*(2*$x + 1)*(3*$x**8 + 12*$x**7 + 8*$x**6 - 18*$x**5 - 10*$x**4 + 24*$x**3 + 2*$x**2 - 15*$x + 5)}]}
# Usage sum_10th 2 -> 1025 # using integer arithmetic
# check answer expr 2**10 = 1025, 1 + 1025 = 1026
# Usage sum_10th 1000000 -> 9.090959090992425e+64 # proc sum_9th for floating pointRef. CRC Standard Mathematical Tables and Formulae [L33 ]
Symbolic Differentiation & Integration in Tcllib Calculus
# commands and procs below should should be pastable into TCL easy eye Console
package require math::calculus
namespace import math::calculus::*
# symbolic differentiation transformed expression in x into dx as expr expression
# x subbed for n in formula proc for sum of fifth powers
proc sum_5thx_power {x} {expr { $x < 1? 0: $x > 1 ? 1 : ($x*$x* ($x+1)*($x+1 )*(2*($x**2)+2*$x-1))/12}}
symdiff {($x*$x* ($x+1)*($x+1 )*(2*($x**2)+2*$x-1))/12} x
returns ((((((2 * $x) * 2) + 2.0) * ((($x * $x) * ($x + 1)) * ($x + 1))) + (((($x * $x) * ($x + 1)) + ((($x * $x) + (($x + $x) * ($x + 1))) * ($x + 1))) * (((2 * ($x ** 2)) + (2 * $x)) - 1))) / 12)
proc pow5th {m n} { set res [round [::math::calculus::integralExpr $m $n 10000 { ((((((2 * $x) * 2) + 2.0) * ((($x * $x) * ($x + 1)) * ($x + 1))) + (((($x * $x) * ($x + 1)) + ((($x * $x) + (($x + $x) * ($x + 1))) * ($x + 1))) * (((2 * ($x ** 2)) + (2 * $x)) - 1))) / 12) }]]}
# Usage pow5th 0 2 -> 33 # pow5th 0 5 -> 4425
# pow5th 0 10000 -> 166716670833332389412864Symbolic Differentiation
# symbolic differentiation transformed expression in x into dx as expr expression
symdiff {1+$x**2} x -> (2 * $x)
symdiff {5+$x**7} x -> (7 * pow($x, 6))
symdiff {$x**4+5*$x**3+4*$x**2-3*$x+2} x -> ((((4 * pow($x, 3)) + ((3 * pow($x, 2)) * 5)) + ((2 * $x) * 4)) - 3.0)
symdiff {(1+$x)**3} x -> (3 * pow((1 + $x), 2))
symdiff {(4+$x)**.5} x -> (.5 * pow((4 + $x), -0.5))
symdiff {1/(1+$x)} x -> -(((1 / (1 + $x)) / (1 + $x)))
symdiff {(1+$x)**(1/3)} x -> (pow((1 + $x), (1 / 3)) * ((1 / 3) / (1 + $x)))Advanced Topics: Math Functions and Constants
Apparently there is considerable computer time saving and effectively extra precision inside the expr w/8.5+. In addition to the predefined expr functions, expr has applications that may define additional math functions and constants by using proc (or any other method, such as interp alias or Tcl_CreateObjCommand to define new commands in the tcl::mathfunc namespace. In addition, an obsolete interface named Introduction_CreateMathFunc() in Tcl C API is available to extensions that are written in >> C++ <<. See [L34 ] & TCL Programming Expr, 2009 & tcl::mathfunc & Additional math functions.
# User loaded procs in the ::tcl::mathfunc namespace invoked inside expr, ref TCL 8.5 plus
# Apparently considerable computer time saving and effectively extra precision inside the expr w/8.5+
proc ::tcl::mathfunc::fib n {expr {$n<2? 1: fib($n-2)+fib($n-1)}} ; expr fib(6)
time {proc ::tcl::mathfunc::fib n {expr {$n<2? 1: fib($n-2)+fib($n-1)}} ; expr fib(6)} 5000
# returns 22.4926 microseconds per iteration
time {expr fib(6) } 5000 # returns 12.0996 microseconds per iteration
proc tcl::mathfunc::factorial x {expr {$x < 2? 1: $x * factorial($x-1)}};expr factorial(100)
time {proc tcl::mathfunc::factorial x {expr {$x < 2? 1: $x * factorial($x-1)}};expr factorial(100) } 5000
expr fac(100) # returns
93326215443944152681699238856266700490715968264381621468592963895217599993229915608941463976156518286253697920827223758251185210916864000000000000000000000000
# time { func factorial 100 } 5000 returns 88.956 microseconds per iteration
time {expr fib(7) } 5000 # 18.6396 microseconds per iteration
proc golden_mean_constant_wordy {} { return [expr {.5*(1. + sqrt(5))}] } # early wordy version
proc golden_mean_constant {} {expr {.5*(1. + sqrt(5))}} # improved, but not using tcl::mathfunc on this one
# Usage golden_mean_constant returns 1.618033988749895
# time { golden_mean_constant} 5000 returns 0.669 microseconds per iteration
# using tcl::mathfunc to generate constant for golden mean
proc tcl::mathfunc::golden_mean_constant2 {} {expr {.5*(1. + sqrt(5))}}
# Usage expr golden_mean_constant2() # returns 1.618033988749895
# Usage time {expr golden_mean_constant2() } 5000 # returns 0.6914 microseconds per iteration2021 Newsflash, Astronomers report Titius-Bode-Based Exoplanet Predictions
Comment: Reference and other articles has 77 predicted planets in 40 exo systems, outside the solar system.
Advanced Topics: Modeling Planetary Distances using Titius-Bode Law and other simple power formulas
Here are some simple formulas modeling planetary distances using the Titius-Bode Law and other power laws. The Titius-Bode Law is primarily of historical interest,refer [L35 ]. The Titius-Bode law estimated rough distances in Astronomical Units (AU) of Planets from the Sun by scaling powers of 2, Johann Elert Bode, pub 1772. There are usually different number assignments for each planet in each formula scheme. The simplest formula number scheme is used here, starting with < Earth = 1... > from Titius-Bode. Although much more is known about planetary distances in modern times, an examination of the original Titius-Bode results gives some fodder for the theory of numerical analysis. The On-Line Encyclopedia of Integer Sequences OEIS refers to the sequences A209257, A003461, and A131500. But the Titius-Bode and other power laws are a good exercise in matching the available data.
Some later fprmulas for planetary distances are the familiar power laws and not that much different from each other, other than some constants. Every 20 or 40 years, the dusty textbooks are thrown out and the wheel is reinvented.
# for starting the adventure to infinity and beyond.
# Titius-Bode set < Earth = 1 ... > as number assignment scheme for planets
# The Asteriod Ceres is included on most number assignment schemes
# Ceres represents the Asteriod belt between Mars and Jupiter.
# The dwarf planet Pluto is included on most number assignment schemes.
proc titius_bode_law_1772 {aa } {expr { (4. + 3 * 2**$aa)*.1 } } # # $nn=l for Earth,2,...
# Other planet number schemes are for power laws are available here, < Mercury = 1 ...>
# from Gaussin (1880) and Armellini (1921)
proc gaussin_formula_1880 {nn} {expr {0.2099 * (1.7226 ** $nn)} } # $nn=l for Mercury,2,...9
proc armellini_formula_1921 {nn} {expr {0.283 * (1.53 ** $nn)} } # $nn=l for Mercury,2,...11
# very interesting, Nicolini transformed planet number scheme in Titius_Bode
# to < Mercury = 1 ...>, refer to Nicolini
proc nicolini_formula_1957 {nn} {expr {0.4 + 0.075 * (2. ** $nn)} } # $nn=l for Mercury,2,...
proc basano_hughes_formula_1979 {nn} {expr {0.285 * (1.523 ** $nn)} } # $nn=l for Mercury, 2,...
# Sven-Ingmar Ragnarsson, 1994, modeled Jupiter and the outer planets to Uranus, separately.
# See the Ragnarsson paper, setting these planet assignment numbers is tricky.
# $nn=0 for Jupiter, 2 = Saturn, 3 = Uranus ....
proc ragnarsson_formula_1979 {nn} {expr {5.203*(((5./2.)**(2./3.))**$nn) )} } # $nn=0 for Jupiter, 2 = Saturn,...
proc list_integers { aa bb} { for {set i 1} {$i<=$bb} {incr i} {lappend boo [* 1. $i ] [* $i 1.]};return $boo}
# usage, list_integers 1 10
# set answer_list_integers = [list 1.0 1.0 2.0 2.0 3.0 3.0 4.0 4.0 5.0 5.0 6.0 6.0 7.0 7.0 8.0 8.0 9.0 9.0 10.0 10.0 ]
proc list_titius_bode { aa bb} { for {set i 1} {$i<=$bb} {incr i} {lappend boo [* 1. $i ] [expr { (4. + 3. * 2**$i)*.1}]};if {$i > $bb} {return $boo}}
# Usage list_titius_bode 1 6
# set answer [ list 1.0 1.0 2.0 1.6 3.0 2.8 4.0 5.2 5.0 10.0 6.0 19.6]
proc list_gaussin_formula { aa bb} { for {set ii 1} {$ii<=$bb} {incr ii} {lappend boo [* 1. $ii ] [expr {0.2099 * (1.7226 ** $ii)} ]};if {$ii > $bb} {return $boo}}
# Usage list_gaussin_formula 1 6
# set answer_gaussin [ list 1.0 0.36 2.0 0.62 3.0 1.07 4.0 1.84 5.0 3.18 6.0 5.48 ]
proc list_armellini_formula { aa bb} { for {set ii 1} {$ii<=$bb} {incr ii} {lappend boo [* 1. $ii ] [expr {0.283 * (1.53 ** $ii)}]};if {$ii > $bb} {return $boo}}
# Usage list_armellini_formula 1 7
# set answer_armellini [ 1.0 0.43 2.0 0.66 3.0 1.013 4.0 1.55 5.0 2.37 6.0 3.63 7.0 5.55 ]
figure . Modeling_Planetary_Distances_log_plot_titius_bode
figure . Modeling_Planetary_Distances_plot_titius_bode_vs_gaussin
Draft for One Liner Program Approach to Validation
gold 10/26/2020. Complex subject may have to start out with some helper procs. See string is and ycl
# {lmap i {1 2 3 4 5 6 7 8 9} { expr { $i*($i+1)/2}
set args { 1 2 3 4 5 6 7 8 9}
if { ![catch {expr $args} result] } { puts "gosh" } # MG , catch should fill $result???
proc tester {args} {{![catch {expr $args} result]} ? 0:lmap i {$args} { expr { $i*($i+1)/2}} # MG derived
# Usage tester 1 2 3 4 5 6 7 8 9 {lmap i {1 2 3 4 5 6 7 8 9} { expr { $i*($i+1)/2}
set args { 1 2 3 4 5 6 7 8 9}
if { ![catch { expr {$args}} result] } { puts "gosh" }
# prints gosh
# $result returns " 1 2 3 4 5 6 7 8 9"
if { ![catch { expr {$args}} result] } { puts "gosh $result" } { puts "read error called out on $result} # MG derived
proc isNumeric x {expr ![catch {expr $x*1}]} # RS
if { [regexp {^[$A-Za-z_]} $i]} {set i $x} :# RS
if {[isNumeric $previous] && [regexp {^[$A-Za-z_]} $i]} {set i $x} :# RS
proc whitelist {a} {return [lreplace $term 0 -1]# take list ,return list without blanks}
# complex logic in expr operator ? in a?b:c>, check of entries of zero in math proc
# 4 conditions being checked, aa =? 0, bb =? 0, $aa > $bb ? , else $aa >| $bb
proc err {aa bb} {expr { $aa == 0|| $bb==0 ? 0: $aa > $bb ? (($aa*1.)/$bb -1.)*100. : (($bb*1.)/$aa
-1.)*100.}}
# Usage examples => err 0 7 r> 0, err 7 0 r> 0 err 5 6 r> 19.9, err 6 5 r> 19.9 # formula sum_5th_power = n*n* (n+1)* (n+1 )* ( 2*n**2 + 2*n -1)/12
# formula correct in proc but no checks on entries
proc sum_5th {n} {return [expr {($n*$n* ($n+1)*($n+1 )*(2*($n**2)+2*$n-1))/12}] }
# internal ? in expr testing for 2 conditions
proc sum_5th_power {n} {expr { $n < 1? 0: $n == 1 ? 1 : ($n*$n* ($n+1)*($n+1 )*(2*($n**2)+2*$n-1))/12}}
# Usage sum_5th_power 0 -> 0 # Usage sum_5th_power 1 -> 1
# Usage sum_5th_power 2 -> 33
# test 4 conditionals might work
proc sum_5th_power2 {n} {expr { $n < 0? 0: $n == 0 ? 0: $n == 1 ? 1: $n == 1 ?1 : ($n*$n* ($n+1)*($n+1 )*(2*($n**2)+2*$n-1))/12}}Advanced Topic, Recursion with Logic
See Playing with recursion by RS on TCL Wiki.
# see Playing with recursion on TCL Wiki
proc ++ x {incr x } # RS
proc -+ x {incr x -1 }
proc = {m n} {string equal $m $n} # RS
# Usage = 1 2 returns 0
# Usage ++ 2 returns 3
# works for strings
# Usage = cat cat returns 1
# Usage = cat dog returns 0
proc -+ x {incr x -1 }
proc ++ x {incr x } # RS
# Usage -+ 5 returns 4
# Usage -+ [++ 1 ] returns 1- on this wiki Playing with recursion + recursive functions
- If we had no expr + expr
- A BASIS FOR A MATHEMATICAL THEORY OF COMPUTATION pdf , 1963, by John McCarthy
Advanced Topic, Sum of Infinite Geometric Series
gold Here is a one liner procedure for sum of infinite geometric series, though the explanation and examples take up more than one line.
proc geoseries1 {aa bb} {expr {abs($bb)<1? $aa/(1.0-$bb) : 0.0}} # AM
# below, older one liner with balky redundant returns and if statement.
# proc geoseries2 {aa bb cc} { if {$bb <= -1||$bb >= 1} { return 0} ;return [ expr $aa / ( 1 - $bb ) ]};
# 27Apr2007,gold,works with etcl
# convergent geometric series if $a != 0 and -1 > $r < 1
# $a is constant multiplier, $r is fraction under exp.
# Series is undefined if r< -1 or r > 1
# $cc is optional number of terms in partial sum.
# If divergent, proc returns zero,
# Usage,set test5 [ geoseries1 15 .2857 ]# test5~~21
# Usage,set test5 [ geoseries1 15 -1.2857 ]# test5~~zero
# Usage,set test5 [ geoseries1 15 1.2857 ]# test5~~zero
# Lets adapt AM's more concise procedure from below
# or the partial sum of a geometric series.
proc geoseries3 {aa bb {cc -1}} {expr {abs($bb)<1? ($aa/(1.0-$bb))-([expr {$cc>0}]*$aa*pow($bb,$cc))/(1-$bb) : 0.0}}
# Usage,set test5 [ geoseries3 15 .2857 1 ]# test5~~15
# Usage,set test5 [ geoseries3 15 .2857 4 ]# test5~~20.8597
# Now, lets define and pseudocode an error formula as
# [ expr { 1 -(estimated)/( ideal & exact ) } ] or
# [ expr {1 - (partial sum of n terms)/(total sum of infinite terms) } ]
# set error [expr {1-[ geoseries3 15 .2857 5 ] / [ geoseries3 15 .2857 ] }]# using default args on later.
# error with 5 terms approaches .002# error with 7 terms approaches .00015
# Vola, more than 7 terms exceeds "slide rule accuracy". AM This can be compacted even more:
# AM won first place above, gold
proc geoseries {aa bb} {expr {abs($bb)<1? $aa/(1.0-$bb) : 0.0}} # AMAdvanced Topics, Extra Credit, But Cited for Public Domain
# picks random element in list, useful for picking random colors & numbers
# Wiki Books Tcl Programming Examples 2005 by Richard Suchenwirth
proc random_list lister {lindex $lister [expr {int(rand()*[llength $lister])}]} # RS cited Public Domain
# Usage random_list { TCL must avoid unbalanced quotes or braces }
# Usage random_list { blue black red yellow violet green blue }
proc fac x {expr {$x<2? 1: $x*[fac [incr x -1]]}} # Cameron Laird cited Public Domain
# Usage lengthy recursion calls possible,
# Usage number results can rapidly exceed computer operating domain
# Usage fac 5 returns 120
# Usage fac 7 returns 5040
proc pow10 x {expr {pow(10,$x)}} # RS cited Public Domain
proc log10 x {expr {log10($x)}} # RS cited Public Domain
proc -log10 x {expr {-log10($x)}} # RS cited Public Domain
proc by100 x {expr {$x/100.}} # RS cited Public Domain
# Start pseudocode and formulas
# pseudocode log2 N =~ 1.442695 * ln N
# pseudocode log2 N =~ 3.321928 * log10 N
# pseudocode log2 defined as ln N / ln 2
# pseudocode log(base) N defined exactly as ln N / ln base
# end pseudocode
proc log2 {nn} { expr {1.*log( $nn) / log (2) } } # DeWi cited Public Domain
# Usage log2 2 returns 1.0
# Usage log2 16 returns 4.0
proc log_any_base {nn base} { expr {1.*log( $nn) / log ($base) } } # DeWi cited Public Domain
# Usagel og_any_base 2 2 returns 1.0
# Usage log_any_base 10 10 returns 1.0
# Usage log_any_base 5 10 returns 0.69897
# simple lambda in TCL is 2 adjacent strings as < operator variable> number
# K comparator is sort of an inverse fork as selector, choice, or decision
proc K {a b} {set a} # RS cited Public Domain, K comparator
# proc lammbda invokes the K comparator in proc K
proc lambda {argl body} {K [set n [info level 0]] [proc $n $argl $body]} # RS cited Public Domain
regsub -all {\d(?=(\d{3})+($|\.))} 1234567.89 {\0,} # RS derived & cited Public Domain
# Usage time { regsub -all {\d(?=(\d{3})+($|\.))} 9999999999999999.99 {\0,} } 5000
# 26.829 microseconds per iteration
proc commified { nn } {regsub -all {\d(?=(\d{3})+($|\.))} $nn {\0,}} # RS cited Public Domain
# Usage commified 123456789 returns 123,456,789
# Usage commified 9999999999999999.99 returns 9,999,999,999,999,999.99
# time {commified 9999999999999999.99} 5000 returns 27.217 microseconds per iteration
# Overhead for wrapping commified was [- 27.217 26.829] or 0.3879 microseconds per iteration Advanced Topic, One Liners Program Approach to OO Object Orientation system
We need a one liners program to trap the maddened Foo_Bat into a large corral. The Foo_Bat has 1 sway_back , 2 tails, 3 heads, 6 horns, 10 legs, and 12 big feet, listed in pseudocode tally. The Foo_Bat has 34 parts in our pseudocode tally. But the command Foo_Bat has been not defined in our console in the current TCL session. There should be a OO command that defines a namespace Foo_Bat. The namespace Foo_Bat should allow instance variables , procedures, commands, evals, and methods. One may set variables and define procs inside the Foo_Bat namespace or Foo_Bat corral. The states of these variables would define the existing Foo_Bat inside the namespace. Such a one liners program would effectively be a wrapper or Foo_Bat sugar for the creation of a namespace. Henceforth, the inside variables would be branded as Foo_Bat:variable_name and the inside procs would be addressed or called as Foo_Bat:proc_name. See Thingy: a one liner program OO Object Orientation System Thingy: a one-liner OO system and Namespace resolution Namespace resolution on unknown command.
A version of the easy eye calculator was loaded with thingy_OO by RS as a testbed for OO Object Orientation methods and other one liner programs in the One Liner Compendium. Also, the modified easy eye calculator has a new self_help instruction window. Aside from pasting one liners programs into the easy eye console during the trial sessions, there was interest in moving instance variables , procedures, commands, evals, and methods between the two separate namespaces and the globals for the console window and the numerical display window.The thingy_OO may be a sugar or crutch for namespaces and moving instance variables across the easy eye windows, but thingy_OO was very robust in the trials of one liners programs on the easy eye calculator. See Easy Eye Calculator [L36 ] and A little calculator & Thingy: a one-liner OO system from RS. Note: The two liners in A little calculator from RS is backed by the incredible power of the entire TCL 8.6 language. If one has helper procs for the display windows and invokes the compiled code and math ops notation in the TCL core and the TCLLIB library.
As understood here with the command <thingy Foo_Bat>, the easy eye calculator now has two separate namespaces, the original liner namespace and the Foo_Bat namespace. We set a new proc for global declaration < Foo_Bat proc > {args} { global e; set e $args}>. In the console display the value of $Foo_Bat::big_feet is 12. But one wishes to move $Foo_Bat::big_feet to the numerical display window. Now $big_feet is non existent in the outer program, but available inside the Foo_Bat namespace. So {Foo_Bat::> $Foo_Bat::big_feet } declares the variable to global, evaluates to 12, and move 12 to the numeric display. Hitting return on the numerical display window returns the value of 12 in two times to the console window.
Easy Eye Testbed Session with thingy_RS & OO
# Start pseudocode tally
# The Foo_Bat has 1 sway_back + 2 tails+ 3 heads+ 6 horns + 10 legs + 12 big_feet
# The Foo_Bat has 34 parts
# End pseudocode tally
proc thingy name {proc $name args "namespace eval $name \$args"} # RS
proc thingy2 name {interp alias {} $name {} namespace eval $name} # MS
thingy Foo_Bat
Foo_Bat set sway_back 1
Foo_Bat set tails 2
Foo_Bat set heads 3
Foo_Bat set horns 6
Foo_Bat set legs 10
Foo_Bat set big_feet 12
Foo_Bat proc corral {x} { expr { $ Foo_Bat::sway_back + $ Foo_Bat::tails + $ Foo_Bat::heads + $ Foo_Bat::horns + $ Foo_Bat::legs + $ Foo_Bat::big_feet }}
Foo_Bat::corral 1 # returns 34
puts " Foo_Bat has $ Foo_Bat::sway_back sway_back + $ Foo_Bat::tails tails+ $ Foo_Bat::heads heads+ $ Foo_Bat::horns horns + $ Foo_Bat::legs legs+ $ Foo_Bat::big_feet big_feet"
# The Foo_Bat has 1 sway_back + 2 tails+ 3 heads+ 6 horns + 10 legs + 12 big_feet
puts " Foo_Bat has [ Foo_Bat::corral 1 ] parts "
# The Foo_Bat has 32 parts
# End of Foo_Bat source code,
# but the Foo_Bat may still lurking
# inside console until session endWhen more than one Foo_Bat is trapped or nesting inside the namespace or corral, one may begin observe the proliferation habits of Foo_Bats. In other words nested or stacked namespaces for Foo_Bats should be possible. The task in pseudocode would be 1) introduce thingy_RS into the namespace Foo_Bat, 2) use the thingy program inside Foo_Bat to create a new baby namespace, 3) load the baby namespace with instance variables and procedures. For task 1), thingy is just another procedure, so Foo_Bat proc thingy name {,...} should load a procedure called Foo_Bat::thingy. If one has Foo_Bat::thingy, the next step 2) would be to load a baby namespace as Foo_Bat::thingy Baby_Foo_Bat. Now for task 3) the namespace Baby_Foo_Bat has come into existent, one can load the baby namespace with variables and procs. For example, load the pi function of AMG into Baby_Foo_Bat as <Foo_Bat::Baby_Foo_Bat proc pi {} {expr acos(-1)}>. In the easy eye console, the command Foo_Bat::Baby_Foo_Bat::pi should return 3.14 rounded.
Observe Caution : Nesting Foo_Bats in Namespace Foo_Bat::Baby_Foo_Bat
source Easy_Eye_Testbed_V3_for_Thingy_RS.tcl
puts "*******************************************************"
puts " Foo_Bat(s) begin nesting here "
puts "*******************************************************"
Foo_Bat proc thingy name {proc $name args "namespace eval $name \$args"}
Foo_Bat::thingy Baby_Foo_Bat
Foo_Bat::Baby_Foo_Bat proc pi {} {expr acos(-1)}
Foo_Bat::Baby_Foo_Bat::pi
puts " Foo_Bat::Baby_Foo_Bat::pi returns [ Foo_Bat::Baby_Foo_Bat::pi ] "
puts "pi and thingy procs both inside the nested namespace Foo_Bat::Baby_Foo_Bat"Figure 1 : Maddened Foo_Bat in Corral
Figure 2 : thingy_OO action in Easy Eye Console Session screenshot 1
Figure 3 : thingy_OO action in Easy Eye Console Session screenshot 2
Figure 4 : Nesting Foo_Bats in Easy Eye Console Session screenshot 3
Figure 5 : Refer to TCLLib section, Following Session is Dependent on TCLLIB Math library
Chart for SI function, Sin(x) / x
One Liners Programs Compendium Si & Ci chart
Draft One Liner Credits
- Wikipedia search engine < doubling time >
- Wikipedia search engine < compound interest >
- Wikipedia search engine < Interest Rates >
- Google search engine < compound interest >
- Book >> Python Crash Course: A Hands-On , by Eric Matthes
- One Liners Programs Pie in the Sky
- One Liners
- One Liners Programs Compendium [L37 ]
- WIKI BOOKS, Programming_Examples pdf
- WIKI BOOKS, Tcl_Programming_Introduction pdf
- license https://creativecommons.org/licenses/by-sa/3.0/legalcode
- creativecommons.org/licenses/by-sa/3.0/
- en.wikibooks.org/wiki/Tcl_Programming_Introduction
- Sample Math Programs Sample Math Programs, item 2, RS
- TCLLIB math::mean is quicker by a third over some homebrew code.
- Additional math functions
- Apple Cray Computer [L38 ].
- https://www.quora.com/What-are-the-most-useful-Swiss-army-knife-one-liners-on-Unix-That-is-what-is-your-favorite-one-liner-command-that-handles-a-task-usually-delegated-to-a-much-more-verbose-program-written-in-a-high-level-language
- http://www.codecodex.com/wiki
- SOURCE CODE SEARCH ENGINES, INCLUDE TCL????
- Google Code Search
- Koders
- Krugle
- Google Code Search
- Koders
- Krugle
- Protecode
- REFERENCES
- http://www.codecodex.com/wiki
- https://www.openhub.net/p?ref=homepage&query=tcl
- https://en.wikipedia.org/wiki/Portal:Computer_programming
- https://en.wikipedia.org/wiki/Portal:Free_and_open-source_software
- https://en.wikipedia.org/wiki/Protecode
- https://en.wikipedia.org/wiki/List_of_search_engines#Source_code
- https://blog.robertelder.org/don-libes-expect-unix-automation-tool/
Credits on One Liner Programs
- Little L Programming Language
- Let's assign with let
- let
- let2
- Easy Eye Calculator [L39 ]
- Tcl the Misunderstood
- Maximum nummeric value from max
- L-Language pdf L , by Larry McVoy:
- One liners Programs Pie in the Sky
- Counting characters in a string
- Playing with recursion
- recursive functions
- If we had no expr
- expr
- little language
- string is
- ycl
- Note on Reposted Tips in Ask13 [L40 ].
- meeting the friendly challenge of Python >>
- wiki.python.org/moin/ Powerful Python One-Liners
- Python Crash Course: A Hands-On, Project-Based Introduction to Programming
- 2019, English,by Eric Matthes
- WIKI BOOKS, Tcl_Programming_Introduction
- license https://creativecommons.org/licenses/by-sa/3.0/legalcode
- creativecommons.org/licenses/by-sa/3.0/
- en.wikibooks.org/wiki/Tcl_Programming_Introduction
- www.tcl-lang.org/man/tcl8.6/TclCmd/for
- Sample Math Programs, item 2, RS
- TCLLIB math::mean is quicker by a third over some homebrew code.
- Additional math functions
- en.wikipedia.org One-liner_program
- One liners of Basic and history, 10_PRINT_121114.pdf
- Summing a list
- Tcllib Contents
- another list comprehension & reference one liner comments
- stackoverflow.com/questions 36832927 using-globs-in-perl-replace-one-liner-in-tcl-script
- www.rexegg.com regex-perl-one-liners
- Regular Expressions Cookbook, Second Edition
- Learning Regular Expressions
- Beyond Regular Regular Expressions
- Mastering Regular Expressions, 3e
- # credit Tcl and Tk Programming for the Absolute Beginner by KURT WALL
- bbcmicro.co.uk on Commodore Basic
- Acorn User One-Line Games (Escape From Voros, Lexxias, Race To Varpon,
- Storm Clouds Over Zaqqit, Zander (AKA Lurch))". bbcmicro.co.uk on Commodore Basic
- blog.eduonix.com, perl_programming,learn-one-liners-perl-programming
- en.wikipedia.org , One-liner_program
- RUN magazine issue 35 on Basic language
- Richard Socher, Perl Scripts And One Liners
- Introduction to Perl One-Liners (PDF), Peteris Krumins
- Perl one-liner if else logic - Stack Overflow
- How to Match Multiple Lines using Regex in Perl One-liners
- By Eric Ma , In Programming, Tutorial
- Time
- How to Measure Performance
- timers
- Category Performance
- see www.altparty.org archive/invi.tcl Setok ref.
- Why Tcl is so much slower than Perl, pros and cons
- Playing with recursion
- Category Numerical Analysis
- TCLLIB numtheory section
- Gauss Approximate Number of Primes and eTCL demo example calculator
- math::numtheory::isprime
- math::numtheory::firstNprimes
- math::numtheory::primesLowerThan
- math::numtheory::primeFactors
- math::numtheory::numberPrimesGauss
- math::numtheory::numberPrimesLegendre
- math::numtheory::numberPrimesLegendreModified
- math::numtheory::differenceNumberPrimesLegendreModified
- On-Line Encyclopedia of Integer Sequences , OEIS
- Andrew Granville, Primes in intervals of bounded length, Joint Math Meeting, Jan 17 2014.
- J. C. Evard, Twin primes and their applications, archived Pdf
- James Maynard, Small gaps between primes, arXiv:1311.4600 , 2013, Annals of Mathematics,
- Babylonian Brothers Inheritance Problems Algorithm and eTCL demo example calculator, numerical analysis
- Babylonian False Position Algorithm and eTCL demo example calculator, numerical analysis
- Chinese Horse Race Problems from Suanshu, DFP, and example eTCL demo calculator, numerical analysis
- [Ancient Egyptian Double False Position Algorithm
- International_Obfuscated_C_Code_Contest [L41 ]
- Spaghetti_code [L42 ]
- Waterfall_model [L43 ]
- Call Procedure Like Fortran Example
- Basic in TCL
- [L44 ] Draft Wikipedia article on One Liners Programs , TCL Tool Control Language
- dbohdan's list of embedded scripting languages
- [L45 ] www.levenez.com history of computer languages
- A little math language revisited
- A little math language
- Tcl Math Syntax is Inferior to JavaScript/Python/Ruby/C/C++/Java/Perl/PHP
- Numerical Analysis in Tcl
- a little proving engine
- Parsing Polish notation
- let
- let - a simpler sugar for expr
- AMG's language ideas
- Let's assign with let
- The L Programming Language or
- Tcl for C Programmers, Oscar Bonilla, Tim Daly, Jr., Larry McVoy
- search keywords <Avoiding Brackets>
- Assign using equals
- Partcl - a minimal Tcl interpreter
- Tiny Tcl 6.8 is a rommable,
- minimal Tcl for embedded applications.
- Basic256, So You Want to Learn to Program?, English pdf
- James M. Reneau, M.S., Shawnee State University
- Portsmouth Ohio USA
- Tcl implementations
- The Very Minimal Tcl Core Command Set
- Does Tcl still fit on 16-bit microcontrollers?
- MicroTcl for Tcl9
- CRC Standard Mathematical Tables and Formulae [L46 ]
- Triangular Number Multiplication Study and demo example TCL calculator, numerical analysis
- Playing Recursion V2 >> demo examples for one liners programs
- Primal Screens— Part Two KWJ
- switch & Tcl Tutorial Lesson 6 [L47 ] [L48 ]
References: Advanced Topics: Modeling Planetary Distances using Titius-Bode Law
- Wikipedia search engine < Titius Bode >
- Wikipedia search engine < Golden Mean >
- Wikipedia search engine < Programming Examples >
- Google search engine < vaporware >
- wikipedia.org/wiki/Titius Bode law
- Article: All Solar system periods fit
- the Fibonacci series and the Golden Ratio.
- Posted: February 20, 2013 by tallbloke
- The Golden Mean In The Solar System,
- Oreste W. Lombard I And Margaret A. Lombardi
- On a Suggested Substitute for Bode’s Law. By M. A. Blagg.
- Communicated by Professor H. B. Turner.
- Planetary distances: a new simplified model
- Sven-Ingmar Ragnarsson, 1994
- Fibonacci Series In The Solar System
- Captain B. A. Read, Canada
- A postulate leading to the Titius-Bode law
- R. Louise
- www.jpl.nasa.gov/edu/pdfs/scaless_reference.pdf
- Schuette, C. H., "Two new families of comets", Pop. Astron. 57, 176-82
- (1949); "Drei weitere Mitglieder der Transplutokometenfamilie", Acta
- Astronomica 15, 11-13 (1965).
- Bode’s Law And Spiral Structure In Nebulae
- By William Sutherland
- A Sedna-like body with a perihelion of 80
- astronomical units
- Chadwick A. Trujillo, Scott S. Sheppard
- Searching For Sedna’s Sisters: Exploring The Inner Oort Cloud
- Megan Schwamb with Advisor: Mike Brown
- A new object at the edge of our Solar System discovered
- by Carnegie Institution for Science
- Modeling Celestial Mechanics Using the Fibonacci Number,
- Robert G. Sacco, 2019
- A Supposed New Law For Planetary Distances, letter,
- Ennio Badolati, 1982, several approaches cited
- Munini and Armellini (1978) , d = 0.283 x 1.52**n, sequence < n = 1,2,... 12 >
- 1880 Gaussin, d~ = 0.2099 x 1.7226**n, (n = 1,2... 9)
- tester formula, d = $K1 x 1.842**n, sequence < n = 1,2,... 12 >
- Planetary distances: a new simplified model
- Sven-Ingmar Ragnarsson
- Using the Inclinations of Kepler Systems to Prioritize New
- Titius-Bode-Based Exoplanet Predictions
- T. Bovaird1,, C. H. Lineweaver, and S. K. Jacobsen, 24 January 2020
- Using the Titius-Bode Relation to Predict the Periods of Kepler’s Missing Planets
- www.hou.usra.edu/meetings/abscicon2015/eposter/7278.pdf
- Scientists Find Evidence of Thousands of ExoPlanets in Distant Galaxy,
- Ryan F. Mandelbaum, 2/05/2018
- wikipedia search engine < Exoplanet Titius-Bode >
- google search engine < Exoplanet Titius-Bode >
Appendix TCL programs and scripts
Timing Equivalent One Liners V2
# pretty print from autoindent and ased editor
# Timing Equivalent One Liners V2
# written on Windows 10 on eTCL
# working under TCL version 8.6
# gold on TCL Club , 8/20/2020
# Ref. WIKI BOOKS, Tcl_Programming_Introduction
# Book Section contrasts one liners
# versus traditional procedural approach
# below contains redundant procs
package require Tk
package require math::numtheory
package require math::constants
package require math::trig
package require math
namespace path {::tcl::mathop ::tcl::mathfunc math::numtheory math::trig math::constants }
set tcl_precision 17
proc pie {} {return [expr acos(-1)]}
console show
console eval {.console config -bg palegreen}
console eval {.console config -font {fixed 20 bold}}
console eval {wm geometry . 40x20}
# uses join, but computer time on some?
proc mean_1 list {expr double([join $list +])/[llength $list]}
# math operators exposed as commands, and the expand operator
proc mean_2 list {expr {[tcl::mathop::+ {*}$list]/double([llength $list])}}
# import the tcl::mathop operators
proc mean_3 list {expr {[+ {*}$list]/double([llength $list])}}
# import the tcl::mathop operators from <Summing a list>
# list add ladd or summing a list
proc ladd_1 {listx} {::tcl::mathop::+ {*}$listx}
# using join in ladd_2 from RS
proc ladd_2 {listx} {expr [join $listx +]+0} # RS
# using expr including non integers from PYK 2016-04-13
proc ladd_3 {listx} {set total 0.0; foreach nxt $listx {set total [expr {$total + $nxt}]}; return $total}
set limit 12
puts "%|table| | printed in|TCL format |% "
puts "&| session| proc & mean value| elements in list | comment, if any|& "
for { set i 0 } { $i <= $limit } { incr i } {
set lister { 1 2 4 5 6 7 8 9 10 }
lappend lister [* $i [pie]]
puts "&|$i | ladd_1 [ ladd_1 $lister ] | $lister | proc timer [ time { set qq [ ladd_1 $lister ]} 5000 ] |&"
puts "&|$i | ladd_2 [ ladd_2 $lister ] | $lister | proc timer [ time { set qq [ ladd_2 $lister ]} 5000 ] |&"
puts "&|$i | ladd_3 [ ladd_3 $lister ] | $lister | proc timer [ time { set qq [ ladd_3 $lister ]} 5000 ] |&"
puts "&|$i | mean_1 [ mean_1 $lister ] | $lister | proc timer [ time { set qq [ mean_1 $lister ]} 5000 ] |&"
puts "&|$i | mean_2 [ mean_2 $lister ] | $lister | proc timer [ time { set qq [ mean_2 $lister ]} 5000 ] |&"
puts "&|$i | mean_3 [ mean_3 $lister ] | $lister | proc timer [ time { set qq [ mean_3 $lister ]} 5000 ] |&"
puts "&|$i | ::math::mean [::math::mean 1 2 4 5 6 7 8 9 10 [* $i [pie]]] | $lister | proc timer [ time { set qq [ ::math::mean 1 2 4 5 6 7 8 9 10 [* $i [pie]] 5000 ]} ] |&"
}
#end Table of Timing 4 Procs
| table | printed in | TCL format | |
|---|---|---|---|
| session | proc & mean value | elements in list | comment, if any |
| 0 | ladd_1 52.0 | 1 2 4 5 6 7 8 9 10 0.0 | proc timer 2.3273999999999999 microseconds per iteration |
| 0 | ladd_2 52.0 | 1 2 4 5 6 7 8 9 10 0.0 | proc timer 5.6311999999999998 microseconds per iteration |
| 0 | ladd_3 52.0 | 1 2 4 5 6 7 8 9 10 0.0 | proc timer 4.3941999999999997 microseconds per iteration |
| 0 | mean_1 5.2000000000000002 | 1 2 4 5 6 7 8 9 10 0.0 | proc timer 13.053599999999999 microseconds per iteration |
| 0 | mean_2 5.2000000000000002 | 1 2 4 5 6 7 8 9 10 0.0 | proc timer 3.0369999999999999 microseconds per iteration |
| 0 | mean_3 5.2000000000000002 | 1 2 4 5 6 7 8 9 10 0.0 | proc timer 2.3805999999999998 microseconds per iteration |
| 0 | ::math::mean 5.2000000000000002 | 1 2 4 5 6 7 8 9 10 0.0 | proc timer 22 microseconds per iteration |
| 1 | ladd_1 55.141592653589797 | 1 2 4 5 6 7 8 9 10 3.1415926535897931 | proc timer 1.7847999999999999 microseconds per iteration |
| 1 | ladd_2 55.141592653589797 | 1 2 4 5 6 7 8 9 10 3.1415926535897931 | proc timer 7.3037999999999998 microseconds per iteration |
| 1 | ladd_3 55.141592653589797 | 1 2 4 5 6 7 8 9 10 3.1415926535897931 | proc timer 1.7285999999999999 microseconds per iteration |
| 1 | mean_1 5.5141592653589795 | 1 2 4 5 6 7 8 9 10 3.1415926535897931 | proc timer 8.3374000000000006 microseconds per iteration |
| 1 | mean_2 5.5141592653589795 | 1 2 4 5 6 7 8 9 10 3.1415926535897931 | proc timer 2.2898000000000001 microseconds per iteration |
| 1 | mean_3 5.5141592653589795 | 1 2 4 5 6 7 8 9 10 3.1415926535897931 | proc timer 2.1674000000000002 microseconds per iteration |
| 1 | ::math::mean 5.5141592653589795 | 1 2 4 5 6 7 8 9 10 3.1415926535897931 | proc timer 6 microseconds per iteration |
| 2 | ladd_1 58.283185307179586 | 1 2 4 5 6 7 8 9 10 6.2831853071795862 | proc timer 1.7618 microseconds per iteration |
| 2 | ladd_2 58.283185307179586 | 1 2 4 5 6 7 8 9 10 6.2831853071795862 | proc timer 6.6627999999999998 microseconds per iteration |
| 2 | ladd_3 58.283185307179586 | 1 2 4 5 6 7 8 9 10 6.2831853071795862 | proc timer 4.0709999999999997 microseconds per iteration |
| 2 | mean_1 5.8283185307179588 | 1 2 4 5 6 7 8 9 10 6.2831853071795862 | proc timer 8.5307999999999993 microseconds per iteration |
| 2 | mean_2 5.8283185307179588 | 1 2 4 5 6 7 8 9 10 6.2831853071795862 | proc timer 2.1261999999999999 microseconds per iteration |
| 2 | mean_3 5.8283185307179588 | 1 2 4 5 6 7 8 9 10 6.2831853071795862 | proc timer 2.3512 microseconds per iteration |
| 2 | ::math::mean 5.8283185307179588 | 1 2 4 5 6 7 8 9 10 6.2831853071795862 | proc timer 5 microseconds per iteration |
| 3 | ladd_1 61.424777960769376 | 1 2 4 5 6 7 8 9 10 9.4247779607693793 | proc timer 1.9702 microseconds per iteration |
| 3 | ladd_2 61.424777960769376 | 1 2 4 5 6 7 8 9 10 9.4247779607693793 | proc timer 7.1285999999999996 microseconds per iteration |
| 3 | ladd_3 61.424777960769376 | 1 2 4 5 6 7 8 9 10 9.4247779607693793 | proc timer 2.6114000000000002 microseconds per iteration |
| 3 | mean_1 6.1424777960769372 | 1 2 4 5 6 7 8 9 10 9.4247779607693793 | proc timer 8.5581999999999994 microseconds per iteration |
| 3 | mean_2 6.1424777960769372 | 1 2 4 5 6 7 8 9 10 9.4247779607693793 | proc timer 2.1989999999999998 microseconds per iteration |
| 3 | mean_3 6.1424777960769372 | 1 2 4 5 6 7 8 9 10 9.4247779607693793 | proc timer 2.4533999999999998 microseconds per iteration |
| 3 | ::math::mean 6.1424777960769372 | 1 2 4 5 6 7 8 9 10 9.4247779607693793 | proc timer 5 microseconds per iteration |
| 4 | ladd_1 64.566370614359172 | 1 2 4 5 6 7 8 9 10 12.566370614359172 | proc timer 1.7842 microseconds per iteration |
| 4 | ladd_2 64.566370614359172 | 1 2 4 5 6 7 8 9 10 12.566370614359172 | proc timer 10.103400000000001 microseconds per iteration |
| 4 | ladd_3 64.566370614359172 | 1 2 4 5 6 7 8 9 10 12.566370614359172 | proc timer 1.9608000000000001 microseconds per iteration |
| 4 | mean_1 6.4566370614359174 | 1 2 4 5 6 7 8 9 10 12.566370614359172 | proc timer 8.8523999999999994 microseconds per iteration |
| 4 | mean_2 6.4566370614359174 | 1 2 4 5 6 7 8 9 10 12.566370614359172 | proc timer 2.0948000000000002 microseconds per iteration |
| 4 | mean_3 6.4566370614359174 | 1 2 4 5 6 7 8 9 10 12.566370614359172 | proc timer 2.2736000000000001 microseconds per iteration |
| 4 | ::math::mean 6.4566370614359174 | 1 2 4 5 6 7 8 9 10 12.566370614359172 | proc timer 5 microseconds per iteration |
| 5 | ladd_1 67.707963267948969 | 1 2 4 5 6 7 8 9 10 15.707963267948966 | proc timer 3.6421999999999999 microseconds per iteration |
| 5 | ladd_2 67.707963267948969 | 1 2 4 5 6 7 8 9 10 15.707963267948966 | proc timer 10.6218 microseconds per iteration |
| 5 | ladd_3 67.707963267948969 | 1 2 4 5 6 7 8 9 10 15.707963267948966 | proc timer 2.3553999999999999 microseconds per iteration |
| 5 | mean_1 6.7707963267948967 | 1 2 4 5 6 7 8 9 10 15.707963267948966 | proc timer 8.4225999999999992 microseconds per iteration |
| 5 | mean_2 6.7707963267948967 | 1 2 4 5 6 7 8 9 10 15.707963267948966 | proc timer 2.1343999999999999 microseconds per iteration |
| 5 | mean_3 6.7707963267948967 | 1 2 4 5 6 7 8 9 10 15.707963267948966 | proc timer 2.1093999999999999 microseconds per iteration |
| 5 | ::math::mean 6.7707963267948967 | 1 2 4 5 6 7 8 9 10 15.707963267948966 | proc timer 5 microseconds per iteration |
Pretty Print Version
Easy Eye Testbed for Thingy_RS and Other One Liner Programs
Here is some starter code for an easy eye calculator as a testbed for one liners programs. The easy eye calculator includes large black font on green background. The human eye is peaked for yellow/green and various ergonomic studies have shown that black font on green background is one of the easiest to read. My small notepad has a linked script and icon for easy eye calculator, posted on the windows desktop of small screen, 22 by 12 cm. One advantage of the easy eye calculator is that the calculations are posted to a console window as a sort of paper tape. The easy eye calculations and text can be cut and paste, saved to a word processor. The easy eye calculator is a compilation of several eval calculators on the TCL Wiki, especially A little calculator from RS. Note: The two liners in A little calculator from RS has the incredible power of the entire TCL 8.6 language. if one has helper procs for the displays and invokes the compiled code and math ops notation in the TCL core and the TCLLIB library. Also see Easy Eye Calculator [L49 ]
A version of the easy eye calculator was loaded with thingy_OO by RS as a testbed for OO methods and other one liner programs in the One Liner Compendium. Also, the modified easy eye calculator has a new self_help instruction window. Aside from pasting one liners programs into the bottom of the easy eye console during the trial sessions, there was interest in moving instance variables , procedures, commands, evals, and methods between the two separate namespaces and the globals for the console window and the numerical display window. See Easy Eye Calculator and eTCL Slot Calculator Demo Example, Numerical Analysis and A little calculator from RS. Note: The two liners in A little calculator from RS has the entire incredible power of the entire TCL 8.6 language, if one has helper procs for the displays and invokes the compiled code and math ops notation in the TCL core and the TCLLIB library.
# pretty print from autoindent and ased editor
# Easy Eye Testbed V3 for Thingy_RS and Other One Liner Programs
# easy eye calculator V3, large black type on green
# used as testbed for one liners programs
# written on Windows 10 on TCL
# working under TCL version 8.6
# base calculator derived from RS & FR
# added cosmetics and extensions for "paper tape"
# gold on TCL WIKI , 10Sep2020
package require Tk
package require math::numtheory
package require math::constants
package require math::trig
package require math
namespace path {::tcl::mathop ::tcl::mathfunc math::numtheory math::trig math::constants }
package provide calculatorliner 1.0
namespace path {::tcl::mathop ::tcl::mathfunc}
set tclprecision 17
namespace eval liner {
console show
proc initdisplay {} {
pack [entry .e -textvar e -width 50 ]
# suggest maintain dead spaces and air gaps near expr, brackets, etc
bind .e <Return> {puts $e;catch {expr [string map {/ *1./} $e] } res; set e $res;puts $res} # RS & FR
}
}
proc linershell {} {
namespace import liner::*
liner::initdisplay
.e configure -bg palegreen
.e configure -fg black
.e configure -font {helvetica 50 bold}
.e configure -highlightcolor tan -relief raised -border 30
focus .e
wm title . "Easy Eye Calculator >> Numeric Display Window "
#. configure -background orange -highlightcolor brown -relief raised -border 30
proc pi {} {
expr acos(-1)
}
proc > {args} {
global e
set e $args}
proc e> {args} {
global e
set e ""}
proc q> {args} {
exit}
}
bind Label <1> {focus %W}
bind Label <FocusIn> {
%W configure -background SystemHighlight -foreground SystemHighlightText
}
bind Label <FocusOut> {
%W configure -background SystemButtonFace -foreground SystemButtonText
}
bind Label <Control-c> {
clipboard clear
clipboard append [%W cget -text]
}
bind Label <Control-p> {
#clipboard clear
clipboard append [%W cget -text]
}
bind Label <Control-q> {
#clipboard exit
clipboard append [%W exit]
}
linershell
# end of initial deck
# add cosmetics below to bottom of file
# added statements above for math ops and TCLLIB library
console show
console eval {.console config -bg palegreen}
console eval {.console config -font {fixed 20 bold}}
console eval {wm geometry . 40x20}
console eval {wm title . " easy eye console, screen grab and paste from console 2 to texteditor"}
console eval {. configure -background orange -highlightcolor brown -relief raised -border 30}
console eval { proc self_helpx {} {
set msg "in TCL, large black type on green
from TCL,
self help listing
Conventional text editor formulas grabbed
from internet screens can be pasted
into green console
# testbed for one liner programs
# loading math ops, TCLLIB components
# suggest maintain dead spaces and air gaps near expr, brackets, etc
# Note spaces near expr statement must be maintained
# or program deck will not work.
# blanks _b must be there
# namespaces liner and Foo_Bat
# creating 4 new commands inside namespace liner
# 1) > moves arguments to numerical display window
# example > 1/9. ;
# console transfer entries to numerical display window
# should be dead space between > and entry
# 1b) left mouse tap on numerical display window
# evals numerical display window to console
# 1c) tap in entry 1/9. on numerical display window
# left mouse tap on numerical display window
# left mouse tap to transfer eval to console pad
# 1d) example transfer text to numerical display window
# from green easy eye console
# > maintain dead spaces and air gaps
# 2) example e> erase numerical display window
# 3) q> conventional exit issued inside liner
# example q> :# invokes exit and quits program
# 4) exit> conventional exit issued inside liner
# example exit> :# invokes exit and quits program
# example also bare exit on console quits program
# > (2*3)+(3*3)
# console transfer entries to numerical display window
# should be dead space between > and entries
# Start pseudocode tally
# The Foo_Bat has 1 sway_back + 2 tails+ 3 heads
# + 6 horns + 10 legs + 12 big_feet
# The Foo_Bat has 34 parts
# console session >> thingy loads Foo_Bat into new namespace or corral
# thingy creating 4 new commands inside Foo_Bat corral
# 1) Foo_Bat::> moves arguments to numerical window
# 2) Foo_Bat::q> conventional exit issued inside Foo_Bat corral
# 3) Foo_Bat::exit> conventional exit issued inside Foo_Bat corral
# 4) Foo_Bat::e> erase numerical display window
# cmd Foo_Bat::> \$Foo_Bat::big_feet moves obj to numerical display window
# example <thingy Foo_Bat> creates namespace Foo_bat
# example <Foo_Bat set tails 2> creates variable \$Foo_Bat::tails
# example <Foo_Bat set heads 3> creates variable \$Foo_Bat::heads
# example <Foo_Bat set horns 6> creates variable \$Foo_Bat::horns
# example <Foo_Bat set big_feet 12> creates variable \$Foo_Bat::big_feet
# example <Foo_Bat Foo_Bat proc corral {x} {body} > creates proc Foo_Bat::corral "
tk_messageBox -title "self_helpxx" -message $msg } }
console eval {.menubar.help add command -label Self_help -command self_helpx }
puts "*******************************************************"
puts " console session >> thingy loads Foo_Bat into corral or namespace "
puts "*******************************************************"
proc thingy name { proc [uplevel 1 namespace current]::$name args "namespace eval $name \$args" } # RS
proc thingy2 name {interp alias {} $name {} namespace eval $name} # MS
thingy Foo_Bat
# creating 4 new commands inside FooBat
# 1) $Foo_Bat::> moves arguments to numerical display window
# 2) $Foo_Bat::q> conventional exit issued inside Foo_Bat
# 3) $Foo_Bat::exit> conventional exit issued inside Foo_Bat
# 4) $Foo_Bat::e> erase numerical display window
Foo_Bat proc > {args} { global e; set e $args}
Foo_Bat proc q> {args} {exit}
Foo_Bat proc exit> {args} {exit}
Foo_Bat proc e> {args} { global e; set e ""}
Foo_Bat set sway_back 1
Foo_Bat set tails 2
Foo_Bat set heads 3
Foo_Bat set horns 6
Foo_Bat set legs 10
Foo_Bat set big_feet 12
Foo_Bat proc corral {x} { expr { $Foo_Bat::sway_back + $Foo_Bat::tails + $Foo_Bat::heads + $Foo_Bat::horns + $Foo_Bat::legs + $Foo_Bat::big_feet }}
Foo_Bat::corral 1 # returns 34
puts " Foo_Bat has $Foo_Bat::sway_back sway_back + $Foo_Bat::tails tails + $Foo_Bat::heads heads + $Foo_Bat::horns horns + $Foo_Bat::legs legs + $Foo_Bat::big_feet big_feet"
# The Foo_Bat has 1 sway_back + 2 tails + 3 heads + 6 horns + 10 legs + 12 big_feet
puts " Foo_Bat has [ Foo_Bat::corral 1 ] parts "
# The Foo_Bat has 34 parts
# end of Foo_Bat thingy_OO code
# but still lurking inside console until session end
puts "*******************************************************"
puts " Foo_Bat(s) begin nesting here "
puts "*******************************************************"
Foo_Bat proc thingy name {proc $name args "namespace eval $name \$args"}
Foo_Bat::thingy Baby_Foo_Bat
Foo_Bat::thingy Teenage_Foo_Bat
Foo_Bat::thingy Doggie_Foo_Bat
Foo_Bat::thingy Cat_Foo_Bat
Foo_Bat::Baby_Foo_Bat proc pi {} {expr acos(-1)}
Foo_Bat::Baby_Foo_Bat::pi
puts " Foo_Bat::Baby_Foo_Bat::pi returns [ Foo_Bat::Baby_Foo_Bat::pi ] "
puts "pi and thingy procs are both inside "
puts " the nested namespace Foo_Bat::Baby_Foo_Bat"
puts "*******************************************************"
puts " >> Observe Caution << "
puts " Nesting Foo_Bats in Namespace Foo_Bat::Baby_Foo_Bat"
puts "*******************************************************"
Foo_Bat::Baby_Foo_Bat proc thingy name {proc $name args "namespace eval $name \$args"}
puts " commands present in Foo_Bat [info commands ::Foo_Bat::* ] "
proc ::Foo_Bat::Baby_Foo_Bat::pie {} {return 3.14159}
puts " commands present in Baby_Foo_Bat [info commands ::Foo_Bat::Baby_Foo_Bat::*]"Equivalent One Liners Programs using tiny_basic_RS.tcl
source tiny_basic_RS.tcl
basic { 10 n=2/7. : 20 print n} # returns 0.2857
basic { 10 n=[/ 2 7. ]: 20 print n} # returns 0.2857
basic { 10 n={2/ 7.}: 20 print n}: 20 print n} # returns 0.2857 Disclaimers and License
Disclaimers: My understanding is that the TCL/TK copyright on the TCL8.6 product is intended to retain editorial control rights , and there is no disagreement with that intention here. As understood here, referencing the TCL/TK copyright pertains to legal notice maintaining the copyright as required by USA law. The Tcl Wiki has international content and other countries may have different rules.
{gold] 10/23/2020 Per Wikipedia entry of single article. The Wikipedia Senior Page editors (not gold) for Wikipedia One Liner Programs will not add above contents to Wikipedia page without the GNU/Wikipedia Commons statements below. [L50 ] I will spare the reader the back and forth from non-lawyers like me. The editor comments on [L51 ] are available on Wikipedia with W. member login. Note: The phrase "One-liner program" is used in the original Wikipedia article with the other computer languages.
{gold] 9/30/2020. This original work and single Tcl/TK Wiki page is also released under the Wikipedia:Text of the GNU Free Documentation License [L52 ] and the Wikipedia:Text of Creative Commons Attribution-ShareAlike 3.0 Unported License [L53 ] in addition to the license or licenses it is already licensed under. Refer to Wikipedia:Licensing update from Wikipedia, the free encyclopedia [L54 ]. As legal precedence, the previous TCL/TK content and example scripts in the Wiki Books TCL Programming by Richard Suchenwirth may have relevance, circa 2005 [L55 ]. """Most of these previous 2005 example scripts first appeared in the Tclers' Wiki""" Also reference 2005 pdf from [L56 ] and later 2018 pdf from Wiki Books version [L57 ]. This release action applies only to the one and only page here and should not be attributed to the rest and other pages of the TCL Wiki and the world wide global internet.
Hidden Comments Section
** Hidden Comments Section **
Please place any comments here with your moniker, Thanks.
Proof Reading here
One Liner Programs Simple One Liner Procedure # One Liner Procedure proc greetings {} {
puts "Hello World!"
} greetings Tcl This is a basic example of a one liner procedure in TCL. The procedure definition is done on a single line, and it simply prints out the message "Hello World!" when called. Random One Liner Procedure # One Liner Procedure proc random_number {} {
expr {rand() * 100}} puts random_number Tcl This one liner procedure generates a random number between 0 and 100 and prints it out. The random number is generated using the rand() function and multiplied by 100. Factorial One Liner Procedure # One Liner Procedure proc factorial n {
expr {$n == 0 ? 1 : $n * [factorial [expr {$n - 1}]]}} puts factorial 5 Tcl This one liner procedure calculates the factorial of a given number. It uses a recursive approach to calculate the factorial, starting with the given number and multiplying it by the factorial of the number minus 1 until it reaches 0. Prime Number One Liner Procedure # One Liner Procedure proc is_prime n {
for {set i 2} {$i <= sqrt($n)} {incr i} {
if {$n % $i == 0} {
return 0
}
}
return 1} puts is_prime 17 Tcl This one liner procedure checks if a given number is prime. It uses a for loop to iterate from 2 to the square root of the given number, checking if the number is divisible by any of the iterated numbers. If it is divisible, it returns 0 (false), indicating that the number is not prime. If the loop completes without finding a divisor, it returns 1 (true), indicating that the number is prime. Text Search One Liner Procedure # One Liner Procedure proc search_text text needle {
if {[string first $needle $text] != -1} {
puts "Found $needle in $text"
}} search_text "Hello World!" "World" Tcl This one liner procedure searches for a specified substring (needle) within a given text. It uses the string first command to find the index of the first occurrence of the needle in the text. If the needle is found, it prints out a message indicating that it was found in the text. These one liner procedures demonstrate the simplicity and conciseness of TCL programming, while still being able to perform useful tasks.
test! seems to work
gold 11/17/2020. added sum of powers procs.
gold 6/8/2021. added interest formulas, removed some copyright notices.
gold 9/27/2021. Switched some comment signs ;# to #. This a big file. Check earlier editions, if not compatible. Maybe obvious, but this page was written on Windows10 Tcl ports including ActiveTCL. I assume reader can cut and paste, what the reader needs and tootle on to his own project and own contribution pages to the TCL Wiki.
| Category Numerical Analysis | Category Toys | Category Calculator | Category Mathematics | Category Example | Toys and Games | Category Games | Category Application | Category GUI |