User Page for Gold
This page is under development. Comments are welcome, but please load any comments in the comments section at the bottom of the page. Please include your wiki MONIKER and date in your comment with the same courtesy that I will give you. Aside from your courtesy, your wiki MONIKER and date as a signature and minimal good faith of any internet post are the rules of this TCL-WIKI. Its very hard to reply reasonably without some background of the correspondent on his WIKI bio page. Thanks, gold 12AUG2020
- User Page for Gold
- Introduction and Greetings
- Calculator approaches in TCL console guis for Windows10
- Projects show up, actions post 1Dec2018
- Revamped Projects under Nikit, actions post 1Dec2018
- Projects under old wiki
- Projects to be updated
- Philosophy On One Liners Programs from One Liners Programs Compendium
- Reposted Tips from AMG & GWM & Wiki for One Liners Programs
- Flexible Push Button Operation in TCL calculator
- 2021 Newsflash, TCLLIB has twin primes and cousin primes routines in TCLLIB:math ticket pipeline
- Use of Global Variables in TCL GUIS
- Maybe partially solved, trouble accessing the TCL WIKI from USA on some restaurant WIFI's?
- Possible Bias of base 2 and 3 in near field?
- Subroutine Template
- sqrt_sum_of_squares
- output for sqrt_sum_of_squares
- Modify discrete events on tugboats_tester3
- Equivalent One Liners V2
- Timing Equivalent One Liners V2
- Table of Timing 4 Procs
- bits and pieces, Testing One Liner Programs
- One Liners from www.codecodex.com/wiki
- Testing One Liner Program for list_twin_primes V2
- Table Results on Twin Primes for 2,4,6,10 Separators
- Older TCL4 reserve
- Sample of TCL One Liner Procedures V2
- Bounds and Limits on the Collatz_Sequences help define the CS. trajectory and envelope
- Draft Wikipedia article on One Liners Programs , TCL Tool Control Language
- CREDITS ON ONE LINERS
- Appendix: One Liner Procs for Modeling Planetary Distances using Titius-Bode Law and other power laws
- Under Titius_Bode , Wikipedia page.
- * Pretty Print Version
- Pseudocode and Equations Section
- Hidden Comments Section
Introduction and Greetings
gold Hi, I'm an old Fortran programmer trying to retread. I actually served time on the IBM punch card machines. I collect old Fortran77 books as a hobby. A lot of guys leaving work would give me their old Fortran77 books. On active, i had a large Fortran collection, almost a library. I would loan and check out Fortran77 books to other employees. Also I programmed a lot in Javascript. Mostly I work on TCL now because i am visually oriented and think that a gui can save a lot of time in engineering calculations.
gold6/2/2021. How did you discover TCL/TK ???? >>
gold About 1996, the Personal Computer PC on my desk, was replaced by a Sun Sparc 20 workstation. I was an engineer and mainly programming in Fortran 77. I had learned QuickBasic, Html, Perl (Unix), and also Javascript. Since the Sparc 20 interface was command line Unix, I looked around for a gui or gui language as an interface to the Sparc 20 workstation. I found Tool Control Language TCL fairly easy to mouse click and invoke executable icons on the Xwindows screen. I even had a gimpy trashcan icon on the screen. I showed my beginner TCL program to a co_worker and he said I had fairly imitated the the PC Windows icon system on a Sparc20 workstation. But this was only about 200 lines of beginner TCL code and fast as greased lightning on a Sparc20! How's that for a sales job on TCL? Then, I wrote small slot calculators in TCL and Javascript on the Sparc20 behind a firewall, which were similar to my later pages on this wiki. Never forget the human brain evolved to hunt rabbits, not Unix critters and command lines. Your eyes and brain modeling/mapping of the outside stims are closer to a gui screen than one might think.
Calculator approaches in TCL console guis for Windows10
gold 2021-09-13. These small TCL graphical user interface guis presented in the wiki for Windows10 may seem trivial math to some, but I have submitted 4 or 5 TCLLIB tickets to improve the TCLLIB math library. For example, the math and logic functions IsOdd, IsEven, IsNegative, IsPositive, figurative_numbers, twin_primes, and Quadratic_Equation_Solution_for_reals were not in the TCLLIB library, as near as I can tell. Maybe these logic functions on integers and Quadratic_Equations on reals are trivial math, but these math functions and quadratic equations show up in some other math languages, offsite TCL programs, and even TCL WIKI pages. As discussion with HE implies, the main idea of TCL or other computer language is that other users can share the faster compiled code rather than homebrew functions. I am retired and since I do not have easy access to a UNIX machine anymore, the only course is to proof the TCL routines on a Windows10 PC with ActiveState TCL.
Npte: Some tickets are closed and functions available in TCLLIB
- closed ticket : find interval of Legendre and 2 other estimated primes from two entries (2019-04-24 19:02:32)
- closed Ticket: find interval of Legendre and 2 other estimated primes from two entries (2019-04-24 19:02:32)
- puts ::math::numtheory::differenceNumberPrimesLegendreModified 100 0
- closed ticket : prime factors of integer Created on: 2017-02-03 18:12:23
- closed ticket : request for the math::number.theory
- a command for prime factoring of a positive integer would be handy.2017-02-03
- could include an int if number was floating and return answer for int(n)
- code from tcl wiki below ordered numbers from low to high, which is good. 2017-02-03
- (Awaiting Moderator Approval) Add Collatz_sequences And Modified Collatz_sequences To Ticket E035b93f36
- Closed Ticket, Gauss / Legendre Functions For Number Of Primes In Tcllib
- Request For Math::number_theory.
- Would Be Handy To Have 3 Prime Number Functions Like Approx_number_primes = N1 / Ln (N1),
- Legendre_primes2 = N1 / (Ln (N1)-1),modified_legendre_primes3 = N1 / (Ln (N1)-1.08366).
- (Awaiting Moderator Approval) New Ticket 5af6381a8b Quadratic Equation Solution, 2 Reals From Muller's Method.
- New Ticket F8adb7a036 Figurate Numbers And Sums Of Powers.
- f8adb7a036 2021-09-18 08:29:50 Patch Open math figurate numbers and sums of powers
- Closed Ticket: Prime Gap Function And Sets Of Twin Primes,cousin Primes,twin Primes
- The first proc listPrimePairs returns a list of pairs of primes that differ by a given number and the second proc
- listPrimeProgressions returns a list of arithmetic progressions of primes that differ by the given number.
- 0ce5a9fc98 2021-03-14 13:21:47 Patch Closed math ::
- special prime gap function and sets of twin primes,cousin primes,twin primes
- df3676c982 2021-03-14 13:31:45 Patch Closed
- math :: geometry trig angle reduction in degrees or radians
- 21fef042b9 2021-03-14 13:33:50 Patch Closed
- math :: geometry add sind ,cosd, etc to geometry functions
- Closed ticket. As of Jul2018, the TCLLIB has developed code for trig angles in degrees,
- trig inverse, and hyper functions in degrees, and angle reduction in radians and degrees.
- ::math::trig::radian_reduced angle
- ::math::trig::degree_reduced angle
- ::math::trig::sind angle
- ::math::trig::cosd angle
- ::math::trig::tand angle
- ::math::trig::cosecd angle
- ::math::trig::secd angle
- ::math::trig::cotand angle
- Open 67b7bafb20 math::combined_market_rate 2019-03-02 05:07:49 math::combined_market_rate
- Open Gamblers_Ruin_Expectation as Probability in TCLLIB math Created on: 2021-09-19 13:34:34
- But I Suppose These Functions Would Be Useful for Proposed Library Collatz_sequences in Tcllib.
Proposed Collatz_sequences And Modified Collatz_sequences Functions In Tcllib.
collatz_sequence_head (27, 4 ) evals 27 82 41 124 collatz_sequence_head (27, 3 ) evals 27 82 41 collatz_sequence_head (27, 2 ) evals 27 82 collatz_sequence_head (27, 1 ) evals 27 , initial entry collatz_sequence_head (10, 3 ) evals 5 16 8 collatz_sequence_tail (27, 4 ) evals 8 4 2 1 collatz_sequence_tail (27, 3 ) evals 4 2 1 collatz_sequence_tail (27, 2 ) evals 2 1 collatz_sequence_tail (27 , 1 ) evals 1, final entry collatz_sequence_tail (10 , 3 ) evals 4 2 1 collatz_sequence_tail (27, 4 ) evals 8 4 2 1 collatz_sequence_max_sequence_value (27) evals 9232? collatz_sequence_max_sequence_value (10) evals 6 collatz_sequence_length (10) evals 6 collatz_sequence_length (27) evals 111? collatz_sequence_generate (10) evals 5 16 8 4 2 1 collatz_sequence_generate (27) evals 27 82 41 124 62 31 ....
Projects show up, actions post 1Dec2018
gold 3Dec2018, pages i thought were gone are showing up, largely under Category Numerical Analysis. as s_ noted, i did not use underscores much in early titles. I must learn on to use the goose search engine better. thanks. i have some updates anyway. I will add self_help button. Revamped TCL programs will be listed as V2. The bulk of these files are being stored locally as OpenOffice file.odt files or rich field text files file.rtf, mainly for spellcheck and larger stored fonts for bad eyes. My understanding is that backup on older files are available through the Internet Archive. Like the example of the Wikipedia, i think that an automated PDF dump of the individual TCL/WIKI pages would be a useful storage item, especially if the PDF included a rack of end attachment of the original unix/ascii text data for the unique WIKI table format and the TCL programs. I am scared i will lose formatted tables copy and I have a bunch.
gold 20Mar2020, Message to Middle Eastern Linguist(s) and museum curators on clay tablets. Have made replica clay tokens and published computer programs using the Sumerian math algorithms on clay tablets. Can contribute some to your museum, if interested???? Some ancient and historic algorithms were loaded into the TCLLIB library for the Tool Control Language (TCL).
Revamped Projects under Nikit, actions post 1Dec2018
- Collatz_Sequences (3*N+1) in Console Example Demo for TCL V2
- HOMA-IR Approximates Average Blood Insulin Resistance in Console Example Demo for TCL V2
- Koch Snowflake Modeling Growth and TCL demo example calculator, numerical analysis
- Modeling Planetary Distances using Titius-Bode Law and and TCL demo example calculator, numerical analysis V2
- Time Fractals in Golden Ratio Proportions and TCL demo example calculator, numerical analysis
- Text Adventure Game and TCL Demo Example [L1 ]
- Parametric Equation Model Vaporware TCL calculator [L2 ]
- One Liners Programs Compendium and TCL demo examples calculations, numerical analysis [L3 ]
- Basic_RS V2 in TCL as partial Basic language interpreter ed
- HgA1c Approximates Average Blood Glucose in Console Example Demo for TCL table format V2 [L4 ]
- Babylonian Expansion Procedure Algorithm and demo example calculator, numerical analysis [L5 ]
- Biology >> Dinosaur Mass from Trackway and TCL demo example calculator, numerical analysis
- Practical_Advice_on_Quotes_and_Brackets_in_TCL
- Biological Mutation Rate and TCL demo example calculator, numerical analysis
- Babylonian_Brothers_Inheritance_Problems_Algorithm and TCL 8.6 demo example calculator, numerical analysis
- Texas Hold Dem Poker Cards, Game, and Probability, numerical analyis
- Ideal Rocket Performance and TCL demo example calculator, numerical analysis
- Old Babylonian Interest Rates and eTCL demo example calculator [L6 ]
- Simple Pulley Forces Tension and eTCL demo example calculator, numerical analysis [L7 ]
- Human Language Root Words & Lexicostatistics Calculator and eTCL Slot Calculator Demo Example, numerical analysis [L8 ]
- Random Walk Equation Slot Calculator Example
- Electronic Failure Rate FITS and eTCL Slot Calculator Demo Example [L9 ]
- Brahmagupta Area of Cyclic Quadrilateral and eTCL demo example calculator
- Babylonian Quarter Square Multiplication procedure algorithm and TCL 8.6 demo example calculator, numerical analysis
- General Tianji' Horse Race Strategy from China and eTCL demo example calculator, numerical analysis
- Sumerian Seeding Rates and eTCL Slot Calculator Demo Example , numerical analysis [L10 ]
- Stonehenge Circle Accuracy Slot Calculator Example [L11 ]
- Rectangular Radio Antenna and etcl Slot Calculator Demo Example
Projects under old wiki
>>>>>> if can't find or link, look older files under category numerical analysis <<<<<<<< >>>>>> for some unk reason, wiki search engine does not push these files to top <<<<<<<<
- Sumerian Pottery Vessel Mass Calculator
- Babylonian Quarter Square Multiplication procedure algorithm and TCL 8.6 demo example calculator, numerical analysis
- Babylonian Cubic Equation Problem and eTCL demo example calculator, numerical analysis
- Babylonian Square rule for Trapezoid Area and eTCL demo example calculator, numerical analysis
- Characteristic lengths and between Biophoton sensors in the Ultraviolet Spectrum and TCL Slot Calculator, numerical analysis
- Stratographic Years Slot Calculator Example, Age of Earth
- Trig Procedures for degree measures as sind, cosd, tand,etc
- Indian Math Bhaskara (1) Sine formula and extensions, history of math
- Kahan compensated summation algorithm and Neumaier variant summation algorithm, numerical analysis
- Game kingdom of strategy
- Babylonian trailing edge algorithm and reverse sequence algorithm for reciprocals, eTCL demo example calculator, numerical analysis
- Babylonian Combined Work Norm Algorithm and eTCL Slot Calculator Demo Example, numerical analysis
- Weighted Decision and example eTCL demo calculator, numerical analysis
- Division into Parts by Multiple Ratios and eTCL demo example calculator, numerical analysis
- Combined Availability and example eTCL demo calculator, numerical analysis
- Chinese Horse Race Problems from Suanshu, DFP, and example eTCL demo calculator, numerical analysis
- Ancient Egyptian Double False Position Algorithm, and example eTCL demo calculator, numerical analysis
- Babylonian Multiplicatiion Algorithm and example demo eTCL calculator, numerical analysis
- Babylonian Weight Riddle Problems and eTCL demo example calculator, numerical analysis
- Babylonian Babylonian Irregular Reciprocal Algorithm and eTCL demo example calculator, numerical analysis
- Babylonian Field Expansion Procedure Algorithm and example demo eTCL calculator, numerical analysis
- Babylonian Trapezoid Bisection Algorithm and eTCL demo example calculator, numerical analysis
- Babylonian False Position Algorithm and eTCL demo example calculator, numerical analysis
- Babylonian Combined Market Rates and eTCL demo example calculator, numerical analysis
- Babylonian Cubic Equation Problem and eTCL demo example calculator, numerical analysis
- Sumerian Base 60 conversion and eTCL demo example calculator, numerical analysis
- Aryabhat Sum of Squares and Cubes and eTCL demo example calculator, numerical analysis
- Sumerian Approximate Area Quadrilateral and eTCL Slot Calculator Demo Example , numerical analysis
- Capsule Surface Area & Volume and eTCL demo example calculator
- Babylonian Number Series and eTCL demo example calculator
- Brahmagupta Area of Cyclic Quadrilateral and eTCL demo example calculator
- Gauss Approximate Number of Primes and eTCL demo example calculator
- Old Babylonian Interest Rates and eTCL demo example calculator
- Twin Lead Folded Dipole Antenna and example demo eTCL calculator
- Refrigerator_Pinyin_Poetry
- Random Poetry Chalkboard
- Oneliner's Pie in the Sky
- Mahjong_Style_Deletion
- Example Linear Interpolation Calculator
- Fuel Cost Estimate Log Slot Calculator Example
- 2010-08-17 19:03:29 Seaching for Babylonian Triplets Slot Calculator Example
- 2010-08-17 15:24:36 Biruni Estimate of Earth Diameter Slot Calculator eample
- 2010-08-16 15:20:57 Fuel Cost Estimate Log Slot Calculator Example
- 2010-08-11 23:43:40 Stratographic Years Slot Calculator Example, Age of Earth
- 2010-08-01 21:11:58 Binomial Probability Slot Calculator Example
- 2010-06-27 21:33:56 Slot_Calculator_Demo
- Chinese Fortune Casting Example Demo
- 2010-08-16 20:04:34 Chinese Sun Stick Accuracy for Console Example
- 2010-08-01 01:15:15 Chinese Iching Hexagrams on Chou Bronzes : TCL Example
- 2010-07-29 01:12:32 Chinese Iching Random Weather Predictions
- 2010-07-18 01:53:25 Chinese Xiangqi Chessboard
- Iching_Fortunes
- application_runner_&_wrapper
- Testing Normality of Pi, Console Example
- horoscope pie plotter
- Stonehenge Circle Accuracy Slot Calculator Example
- Call Procedure Like Fortran Example
- Stonehenge Circle Accuracy Slot Calculator Example
- Drake Intelligent Life Equation Slot Calculator Example
- Sumerian Equivalency Values, Ratios, and the Law of Proportions with Demo Example Calculator
- Piece wise Profits and eTCL Slot Calculator Demo Example
- Drake Intelligent Life Equation Slot Calculator Example
- Stonehenge Circle Accuracy Slot Calculator Example
- Stonehenge Circle Accuracy Slot Calculator Example
- Babylonian Sexagesimal Notation for Math on Clay Tablets in Console Example
- Call Procedure Like Fortran Example
- Canvas Object Movement Example http://wiki.tcl.tk/26626
- Drake Intelligent Life Equation Slot Calculator Example
- Ellipse Properties Slot Calculator Example
- Sea Island Height Slot Calculator Example
- Captioning Photo Image under Pixane Example
- Timing Photo Image Loading under Pixane
- Poker Probability and Calculator Demo Example
- Canvas Object Movement Example
- Generic Calculator Namespace Package Example
- Sumerian Circular Segment Coefficients and Calculator Demo Example
- Tonnage of Ancient Sumerian Ships and Slot Calculator Demo Example
- Heat Engine Combustion and Calculator Demo Example
- Rectangular Radio Antenna and etcl Slot Calculator Demo Example
- Sumerian Equivalency Values, Ratios, and the Law of Proportions with Demo Example Calculator
- Sumerian Construction Rates and eTCL Slot Calculator Demo Example
- Piece wise Profits and eTCL Slot Calculator Demo Example
- Sumerian Coefficients in the Pottery Factory and Calculator Demo Example
- Sumerian Equivalency Values, Ratios, and the Law of Proportions with Demo Example Calculator
- Sumerian Coefficients at the Weavers Factory and eTCL Slot Calculator Demo Example
- Sumerian Coefficients at the Bitumen Works and eTCL Slot Calculator Demo Example edit
- Sumerian Beveled Bowl Volume and eTCL Slot Calculator Demo Example
- Sumerian Population Density and eTCL Slot Calculator Demo Example
- Babylonian Sexagesimal Notation for Math on Clay Tablets in Console Example
- Easy Eye Calculator and eTCL Slot Calculator Demo Example, Numerical Analysis
- Piece wise Profits and eTCL Slot Calculator Demo Example
- Paper & Felt Rolls and eTCL Slot Calculator Demo Example
- Human Language Root Words & Lexicostatistics Calculator and eTCL Slot Calculator Demo Example, numerical analysis
- Sumerian Workday Time & Account Calculator and eTCL Slot Calculator Demo Example, numerical analysis
- contribution to Counting Elements in a List
- contribution to A Program That Learns
- contribution to Simple Canvas Demo
- contribution to lremove
- added many pictures to other pages
- added pix to A fancier little calculator
- added pix to 3 Triangles
- Sumerian Sheep and Herd Animal Calculator and eTCL Slot Calculator Demo Example, numerical analysis
- Probability Exponential Density Calculator and eTCL Slot Calculator Demo Example, numerical analysis
- Electronic Failure Rate FITS and eTCL Slot Calculator Demo Example
- Sumerian Seeding Rates and eTCL Slot Calculator Demo Example , numerical analysis
- Sumerian Porters Pay Formula and eTCL Slot Calculator Demo Example, numerical analysis
- One Dimension Heat Flow Model and eTCL Slot Calculator Demo Example, numerical analysis
- Sumerian Surveyor Area Formula and eTCL Slot Calculator Demo Example, numerical analysis
- Babylonian Sexagesimal Notation for Math on Clay Tablets in Console Example
- Binomial Probability Slot Calculator Example
- Call Procedure Like Fortran Example
- canvas Object Movement Example
- Captioning Photo Image under Pixane Example
- Chinese Fortune Casting Example Demo
- Chinese Iching Hexagrams on Chou Bronzes : TCL Example
- Chinese Sun Stick Accuracy for Console Example
- Command Line Calculator in Namespace Package Example
- Crater Production Power Law Slot Calculator Example
- Drake Intelligent Life Equation Slot Calculator Example
- Ellipse Properties Slot Calculator Example
- Estimating Mountain Height Using Look Angles, Etcl Console Example
- Example Linear Interpolation Calculator
- Finding Seked Angles of Ancient Egypt, Console Example
- Fuel Cost Estimate Log Slot Calculator Example
- Generic Calculator Namespace Package Example
- Heat Engine Combustion and Calculator Demo Example
- Piece wise Profits and eTCL Slot Calculator Demo Example
- Poker Probability and Calculator Demo Example
- Random Walk Equation Slot Calculator Example
- Rectangular Radio Antenna and etcl Slot Calculator Demo Example
- Sanskrit Number Words Handling in Formulas and Demo Calculator Example
- Sea Island Height Slot Calculator Example
- Seaching for Babylonian Triplets Slot Calculator Example
- Simple Reliability Slot Calculator Example
- Stonehenge Circle Accuracy Slot Calculator Example
- Stratographic Years Slot Calculator Example, Age of Earth
- Sumerian Equivalency Values, Ratios, and the Law of Proportions with Demo Example Calculator
- Sumerian Beveled Bowl Volume and eTCL Slot Calculator Demo Example
- Sumerian Circular Segment Coefficients and Calculator Demo Example
- Sumerian Coefficients at the Bitumen Works and eTCL Slot Calculator Demo Example edit
- Sumerian Coefficients at the Weavers Factory and eTCL Slot Calculator Demo Example
- Sumerian Coefficients in the Pottery Factory and Calculator Demo Example
- Sumerian Construction Rates and eTCL Slot Calculator Demo Example
- Sumerian Population Density and eTCL Slot Calculator Demo Example
- Testing Normality of Pi, Console Example
- Tonnage of Ancient Sumerian Ships and Slot Calculator Demo Example
- Sumerian Bronze & Alloy Calculator with demo examples eTCL numerical analysis
- Population Density Rectangular City Calculator and eTCL Slot Calculator Demo Example
- Over-21 Game Shell and eTCL Slot Calculator Demo Example , numerical analysis
- Sales Optimal Lot Order Size and eTCL Slot Calculator Demo Example
- Over-21 Game Shell and eTCL Slot Calculator Demo Example , numerical analysis
- Sales Optimal Lot Order Size and eTCL Slot Calculator Demo Example
- Spare Parts from Normal Distribution and eTCL Slot Calculator Demo Example , numerical analysis
- Sumerian Beer Ingredients and eTCL Slot Calculator Demo Example , numerical analysis
- Sumerian Coefficients at the Dog Keepers and eTCL Slot Calculator Demo Example , numerical analysis
- Timing Photo Image Loading under Pixane
- Babylonian Shadow Length & Angles and eTCL Slot Calculator Demo Example, numerical analysis
- Sumerian Surveyor Area Formula and eTCL Slot Calculator Demo Example, numerical analysis
test below
Babylonian Sexagesimal Notation for Math on Clay Tablets in Console Example Binomial Probability Slot Calculator Example Biruni Estimate of Earth Diameter Slot Calculator eample Chinese Fortune Casting Example Demo Chinese Sun Stick Accuracy for Console Example Command Line Calculator in Namespace Package Example Crater Production Power Law Slot Calculator Example Drake Intelligent Life Equation Slot Calculator Example Easy Eye Calculator and eTCL Slot Calculator Demo Example, Numerical Analysis Ellipse Properties Slot Calculator Example Fuel Cost Estimate Log Slot Calculator Example Generic Calculator Namespace Package Example Heat Engine Combustion and Calculator Demo Example Human Language Root Words & Lexicostatistics Calculator and eTCL Slot Calculator Demo Example, numerical analysis Mahjong_Style_Deletion Oil Molecule Length Calculator and eTCL Slot Calculator Demo Example, numerical analysis Oneliner's Pie in the Sky Paper & Felt Rolls and eTCL Slot Calculator Demo Example Penny Packing Calculator and eTCL Slot Calculator Demo Example, numerical analysis Piece wise Profits and eTCL Slot Calculator Demo Example Planet Mass Calculator and eTCL Slot Calculator Demo Example, numerical analysis Poker Probability and Calculator Demo Example Random Walk Equation Slot Calculator Example Rectangular Radio Antenna and etcl Slot Calculator Demo Example Sanskrit Number Words Handling in Formulas and Demo Calculator Example Sea Island Height Slot Calculator Example Seaching for Babylonian Triplets Slot Calculator Example Simple Reliability Slot Calculator Example Slot_Calculator_Demo Stonehenge Circle Accuracy Slot Calculator Example Stratographic Years Slot Calculator Example, Age of Earth Sumerian Equivalency Values, Ratios, and the Law of Proportions with Demo Example Calculator Sumerian Beveled Bowl Volume and eTCL Slot Calculator Demo Example Sumerian Circular Segment Coefficients and Calculator Demo Example Sumerian Coefficients at the Bitumen Works and eTCL Slot Calculator Demo Example edit Sumerian Coefficients at the Weavers Factory and eTCL Slot Calculator Demo Example Sumerian Coefficients in the Pottery Factory and Calculator Demo Example Sumerian Construction Rates and eTCL Slot Calculator Demo Example Sumerian Paint & Bitumen Coating and eTCL Slot Calculator Demo Example Sumerian Population Density and eTCL Slot Calculator Demo Example Tonnage of Ancient Sumerian Ships and Slot Calculator Demo Example
Projects to be updated
Sumerian Pottery Vessel Mass Calculator, can not find in new wiki system Babylonian Square rule for Trapezoid Area and eTCL demo example calculator, numerical analysis Indian Math Bhaskara (1) Sine formula and extensions, history of math Kahan compensated summation algorithm and Neumaier variant summation algorithm, numerical analysis Sumerian Counting Boards, multiplication operation placement strategy, and eTCL demo example, numerical analysis Babylonian Combined Work Norm Algorithm and eTCL Slot Calculator Demo Example, numerical analysis Stonehenge Circle Accuracy Slot Calculator Example Drake Intelligent Life Equation Slot Calculator Example Sumerian Equivalency Values, Ratios, and the Law of Proportions with Demo Example Calculator Piece wise Profits and eTCL Slot Calculator Demo Example Sumerian Sheep and Herd Animal Calculator and eTCL Slot Calculator Demo Example, numerical analysis Electronic Failure Rate FITS and eTCL Slot Calculator Demo Example Sumerian Seeding Rates and eTCL Slot Calculator Demo Example , numerical analysis Command Line Calculator in Namespace Package Example Example Linear Interpolation Calculator Sumerian Equivalency Values, Ratios, and the Law of Proportions with Demo Example Calculator Sumerian Beveled Bowl Volume and eTCL Slot Calculator Demo Example Population Density Rectangular City Calculator and eTCL Slot Calculator Demo Example Sales Optimal Lot Order Size and eTCL Slot Calculator Demo Example Over-21 Game Shell and eTCL Slot Calculator Demo Example , numerical analysis Sumerian Beer Ingredients and eTCL Slot Calculator Demo Example , numerical analysis Easy Eye Calculator and eTCL Slot Calculator Demo Example, Numerical Analysis Paper & Felt Rolls and eTCL Slot Calculator Demo Example Human Language Root Words & Lexicostatistics Calculator and eTCL Slot Calculator Demo Example, numerical analysis Sumerian Workday Time & Account Calculator and eTCL Slot Calculator Demo Example, numerical analysis Old Babylonian Interest Rates and eTCL demo example calculator Capsule Surface Area & Volume and eTCL demo example calculator Babylonian Square rule for Trapezoid Area and eTCL demo example calculator, numerical analysis Sumerian Coefficients at the Weavers Factory and eTCL Slot Calculator Demo Example Sumerian Population Density and eTCL Slot Calculator Demo Example
Philosophy On One Liners Programs from One Liners Programs Compendium
I remember when my teenage sister would ask about a math problem. I would lead up and carefully explain this and that algebra proposition. But my sister would say " I just want the answer!" In most engineering problems, there is an advantage in finding the answer in an approximate solution, say slide rule accuracy or 4 significant places. For example, using the old slide rule, one would make a preliminary pencil calculation and approximate answer to set the decimal point, before using the slide rule accuracy to 4 significant places. If one thinks of TCL as primarily as a graphical gui language, then the one liners programs are best used to check the preliminary math concepts. One liners programs and initial console programs are often used to check the math concepts and generate testcases before loading the calculator gui shell.
In planning any software, it is advisable to gather a number of testcases to check the results of the graphical user interface gui program. The results of the testcases are estimated using the hand calculations and then checked in the TCL gui calculator. Pseudocode and equations are developed from the hand calculations and theory. One liners procedures and small console programs are written to check or proof the alternate subroutines or procedures, rather than keeping the unblessed code and comment lines in the main gui calculator. Finally the improved or alternate subroutines are loaded into the gui calculator. The TCL gui or slot calculator is effectively a shell program to input entries, host calculation routines, maintain housekeeping procedures, and display results. Additional significant figures are used to check the TCL calculator, not to infer the accuracy of inputs and product reports.
Reposted Tips from AMG & GWM & Wiki for One Liners Programs
The beginner TCL procedure on the pi circle constant was corrected to proc pi {} {expr acos(-1)} ;# AMG. One Liners Programs should avoid using temporary variables like {set temp 3.14:if {$temp=3.14} {return 1};return $temp}. Temporary variables may cause more time delay, more complication, and possible confusion to reader. The return value of a Tcl procedure is inherited from the return value of the last command to execute within that procedure. Therefore, many uses of the return command are redundant. If one insists on temporary variables, be aware that it is perfectly legal for a proc and a variable to have the same name. You could have said "set pi [pi]". For safety and efficiency, always be sure to brace your expr-essions! Heh, I neglected to brace my expression in [pi], but that's one of the extremely rare cases where it won't matter: no spaces, no substitutions. Bracing does two things: One, when the entire expression is a single word (single argument), it can be bytecode-compiled. Two, if substitutions are performed by expr only and not Tcl itself, injection attacks are prevented. Since the expr command has an internal if conditional, ? in a?b:c sic, try using the internal if <?> in expr rather than a separate IFstatement. Avoid using separate if statements and temporary variables for brevity. The args variable is also useful tool in one liners programs for inputting multiple data or lists of words. Another strategy is to keep track of possible error checks and testcases for low, middle, and high values over the range of operation of the oneliners program. An initial check for zero division or series start at one may be installed in the expr ? conditional. A simple credit for a one liner program may use a semicolon with comment sign <;#> at statement end, which should not degrade program execution. Using the time function in TCL will give even more insights into one liners programs, also see Time. In One liners Programs Pie in the Sky, one can see the advice of GWM on the importance of timing your code and procedures. Usually, invoking math ops, TCLLIB library, and other precompiled libraries can save an average of 1/3 time over big data chores. The time savings are not always obvious on small quantities of data. Performance of one liners programs may suffer degradation due to lengthy recursion calls and limits on the number of procedure recursion calls. The shorter the script, the faster and more reliable is the script. Dependence on math operator notation, helper procedures, math check examples, degradation due to lengthy recursion calls, and special library functions should be noted in the comment lines. The examples on this wiki page include code lines that might be incompatible, inefficient, or redundant if installed in the same program. As discussed, the local math procedures in scripts and one-line procedures may not be as fast and efficient as importing mathop , mathfunc, and math, so check with the precompiled code in the TCL core and TCLLIB libraries first, then homebrew your one-line programs and scripts.
Flexible Push Button Operation in TCL calculator
gold 10/7/2018. Technical note on TCL calculator buttons addressing the reference ASK12 of 2017-02-19 . Many complex math programs have either initialize, refresh, or reset routines to force correct behavior, using calculator buttons. Of course, a very good feature of TCL is that new variables as number types do not have to be initialized prior to use. Repeating, setting a new number variable to 0 or 1 is not necessary prior to using the variable. I confess that habits brought from prior learned languages and 40 years ago are hard to change. Most of my gui programs on this wiki have a flexible button procedure (on changing labels and resetting variables prior to calculations). Where the program defaults are recalled, canvas colors/features/variables/clear displays are reset prior to ( in push button list) calculation. The buttons on the calculator are not limited to a single action proc or single shot. A button command may call multiple statements and procs like ::ttk::button .test4 -text "Test_wild_case3" -command {clearx; refresh_canvas_x .cv; fillup 120. 12.0 15.0 1. 1. 1. 1. 104.0; set global_variable 9999.;solve_routine;printout_routine;# need semicolons here; exit}. This is effectively a separate program or subprogram installed as list of procedures in a button.
The TCL language is very flexible, and as experiments, the button may invoke a do while routine to call the listed button procs multiple times like the infinite repeater (SiFi). The button may invoke command and call procedures for a random number of times and random solutions, like nerve and muscle firings from the human brain in thought and speech (not SiFi). For cosmetics, the button may set colors, frame width, canvas objects, and variables with the random proc lpick from RS on the wiki. As long as duplicate frames, duplicate canvas, pack managers, and channels are not confused reference the original program, one can load secondary and entire procs into the button list. Returning to the conventional use of resetting variables, the button refresh and initialize tactic should work across the TCL versions, at least in the versions tested (TCL8.5, and TCL8.6).
Most of the testcases involve experiments or models, using assumptions, and rules of thumb. For the push buttons in the TCL calculator, the recommended procedure is push testcase and fill frame, change first three entries etc, push solve, and then push report. Report allows copy and paste from console to conventional texteditor. For testcases in a computer session, the TCL calculator increments a new testcase number internally, eg. TC(1), TC(2) , TC(3) , TC(N). The testcase number is internal to the calculator and will not be printed until the report button is pushed for the current result numbers. The current result numbers should be cleared either on the clear button or on the next solve button.
2021 Newsflash, TCLLIB has twin primes and cousin primes routines in TCLLIB:math ticket pipeline
gold 5/13/2021.
closer: arjenmarkus AM
Emailed icomment from AM: I used the sample code to create two new procedures:
listPrimePairs listPrimeProgressions
The first proc listPrimePairs returns a list of pairs of primes that differ by a given number and the second proc listPrimeProgressions returns a list of arithmetic progressions of primes that differ by the given number.
Use of Global Variables in TCL GUIS
gold 12Dec2018. Global variables, regular expressions, and namespaces are considered advanced features of the Tool Control Language (TCL), according to Brent Welch in Practical Programming in TCL and TK. If global variables are an advanced feature of TCL, as indexed and taught after the beginner TCL topics in most TCL textbooks, then reasonably the use of global variables should be explored and discussed on the wiki. After a number of searches on the wiki and reference books, the topics of regular expressions and namespaces are adequately explored on the wiki and available textbooks. In opinion, the use of global variables in TCL programs should not be restricted to a narrow viewpoint, and the use of global variables could be a very rich vein of interest for the advanced student of programming. As an engineer with 35 years experience in Fortran, Basic, Javascript, and other computer languages, the author is familiar with self-appointed gatekeepers and the other anonymous ad hominem methods of NDH. NDH means “not done here”, “not done here in our shop”, or “not done here in my programming style”. Global variables in TCL are equivalent to the common variable statements in Fortran and Basic. The use of global variables might be called “sideloading" for data subroutines. Ref Fortran77, the large number crunching programs with 2E5+ statements in Fortran used global variables or common variable declarations as an alternate way or “programming style” to transfer or sideload information between subroutines. The other data transfer method for subroutines was discussed by Brent Welch etc in the proc command arguments or top loading in the introductory or beginner TCL material.
gold 12Dec2018. Of course, each alternate way of data information transfer in toploading and sideloading data subroutines has its own advantages and disadvantages. As most TCL users know, TCL tends to be a more compact language than Fortran77. However, the global declarations in the small TCL graphical user interface guis written for numerical analysis on this wiki have exactly the same common variable structure and same program organization as the giant Fortran number crunchers.
gold 12Dec2018. There are two alternate methods of loading TCL subroutines, known as proc arguments (top loading) and global variables (side loading). In engineering terms, the TCL global variable methods and the Fortran common variables are an economy of scale for large programs. In other words, top loading a data subroutine for a small program with a limited number of variables and a limited number of subroutines is about as efficient as global variables (side loading). When a large program has the number of variables approaching 25 variables and the total number of subroutines approach 20 subroutines, then global variables or common variables become an more attractive alternative data transfer between subroutines and a more efficient use of the programmer's time. This principle is independent of language type, and equally true for the TCL, Fortran, and other computer languages. For example, many scientific Fortran programs had a specialized subroutine for constants, including the gravity constant, speed of light, etc. If the gravity constant was used in 15 subroutines, it was easier to declare the gravity constant as a common variable in a constants subroutine, and then make a one time change in the value of gravity constant in one subroutine of constants than making the same change for the gravity constant in 15 subroutines. If one knows than the sequence of slot variables {$side1,$side2,$side3...$side8...$side_N} and other constants are TCL global variables throughout the subroutines, one can easily refer to these global values in a specialized printout report subroutine. One can also load these global values in formulas for printout and separate calculations on the fly. For a side loading example in a new subroutine, proc newby {} {global side1 side2 side3; puts <* $side1 $side2 $side3>;return <+ $side1 $side2 $side3>}. The alternative top loading would be proc newby {side1 side2 side3} { puts <* $side1 $side2 $side3>;return <+ $side1 $side2 $side3>}. Both subroutine methods work for small TCL programs with the roughly same amount of typing. Remember in top loading, one would have to make other changes in the invoking statement or proc argument statement for the subroutine. One might point out that loading more than 25 variables in either an invoking statement or proc statement is not a trivial exercise to kept correct and cued properly. For another example, a specialized subroutine for printing out variables might use s set of global variables as proc printout {} { global side1 side2 side3; puts $side1; puts $side2; pouts <* side1 side2 side3>; puts "conversion to centimeters"; puts <* $side1_inches 2.54 >; }. A specialized printout subroutine with globals previously declared is faster in development and checking numeric formulas in experience, especially where conversion of units like inches and centimeters is useful for checking the results of the program in older textbook problems.
In opinion, a set of the same global statements in numerous routines are easier to keep organized. The condition of using global variables in method is that the user understands that not all variables are invoked over all the numerous subroutines. Therefore, in the case of multiple variables > 25 and multiple subroutines >20 in a large program, changing a constant variable in a large number of subroutines, little to do in the proc argument statements and invoking the subroutines, and the availability of the global variables throughout the program means less time spent on changes for the programmer. For terms of TCL presentation on the wiki, the slot variables could be changed inside the subroutine to recognizable names in variables for the calculations and quicker comprehension of the reader. In opinion, global variables are a more efficient use of the programmers time for a quick assembly of a working gui or installing a new working subroutine in a large TCL program.
gold 12Dec2018. The author is still learning TCL. These small TCL graphical user interface guis presented in the wiki have gone through an evolution of about twenty years, including numerous unpublished Javascript and TCL guis behind a firewall before joining the wiki. The suggestions from the wiki members have been of great help and these TCL guis have continued to improve. The guis are experimental numerical analysis in nature, and not every early TCL gui or program written over the twenty year period has the same global variable features, structured programming, or beauty spots of the TCL gui genre. The author keeps hearing that TCL is not a number crunching language or an outdated language from non-users. But in the instance of the TCL global variables, the TCL globals have the equivalence of the common statements and common variables in the data subroutines of giant Fortran number crunchers.
Maybe partially solved, trouble accessing the TCL WIKI from USA on some restaurant WIFI's?
gold 7/16/2020, Report so far, in coordination with ActiveState Support [email protected]
gold 08Jul2020. Don't know if other members of TCL Club have this problem, but the author is having great difficulty in accessing this TCL WIKI, since the TCL WIKI and other download TCL programming sites on public WIFI are blocked in the USA. Accordingly, the USA based search engines are apparently not accessing the TCL programming sites. Frantically, the blocked TCL sites will affect the availability,promulgation, and succe$$ of the TCL language. Believe that the TCL language has much to offer mankind, if the TCL language and its amazing utility are not blocked to mankind by gatekeepers, iconoclasts, and bookburners in the USA.
many thanks for help. I am still locked out from easy access to TCL Wiki. but i will report your efforts to the TCL WIKI. Is there an address to resolve issues with ATT ? . I tried to contact ATT, but there is merry-gr on that website. thanks again,gold
Sent with ProtonMail Secure Email.
‐‐‐‐‐‐‐ Original Message ‐‐‐‐‐‐‐ On Thursday, August 13, 2020 2:50 PM, ActiveState Support <[email protected]> wrote:
Hi Gold
I'm not sure if you've been able to work around this or have it fixed yet. I can still see "Error 1000" issues on Cloudflare though with the aliased tcl.activestate.com. Maybe that domain change is being detected as a cross-site redirection attempt and blocked for that.
I'm not clear why, but there is a difference between how wiki.tcl-lang.org and tcl.tk resolve. Maybe that was intended to work like a backup site, or maybe something is out of sync:
:~$ host tcl.activestate.com tcl.activestate.com is an alias for wiki.tcl-lang.org. wiki.tcl-lang.org has address 104.18.184.65 wiki.tcl-lang.org has address 104.18.183.65 wiki.tcl-lang.org has IPv6 address 2606:4700::6812:b841 wiki.tcl-lang.org has IPv6 address 2606:4700::6812:b741 :~$ host wiki.tcl-lang.org wiki.tcl-lang.org has address 104.18.183.65 wiki.tcl-lang.org has address 104.18.184.65 wiki.tcl-lang.org has IPv6 address 2606:4700::6812:b741 wiki.tcl-lang.org has IPv6 address 2606:4700::6812:b841
:~$ host www.tcl.tk www.tcl.tk has address 104.16.56.90 www.tcl.tk has address 104.16.33.94 www.tcl.tk has IPv6 address 2606:4700::6810:385a www.tcl.tk has IPv6 address 2606:4700::6810:215e
whois 104.16.56.90 and whois 104.16.33.94host reports that's Cloudflare. whois 104.18.183.65 and whois 104.18.184.65 also reports Cloudflare
Best regards,
Technical Support Engineer ActiveState Software
APN What URL are you using to access? The tcl.tk domain is problematic (from the blocking perspective), the official name is now wiki.tcl-lang.org. Do you have problems with that domain as well?
gold 7/11/2020. Thanks for feedback. Possibly problem is default security setting on browser or virus firewall security going into a WIFI proxy server. Realize the TCL CLUB is not a 9 to 5, but this item is really cutting down my production and access to TCL references. But the browsers are changing into complexity, pretty fast for a retiree. Quotes """ If you don't believe you should be using a proxy server: Go to the Dissenter menu > Settings > Show advanced settings… > Change proxy settings… > LAN Settings and deselect the "Use a proxy server for your LAN" checkbox. UNQuote"""" The strange thing is that I can see https://wiki.tcl-lang.org/welcome and https://sourceforge.net/projects/tcllib/ at Starbucks coffee and some "bar" WIFI's, but I can not see the TCL Wiki same at Mcdonalds, Wendy's, and some other quick stop WIFI's.
7/13/2020. trouble coming from Macdonald restaurant etc ATT WIFI?? https://login-mcd-cluster.prd.....snantx.attwifi.com/g error messege found after site log. SIC http://tcl.activestate.com/software/tcllib/tcl.activestate.com’s server IP address could not be found. Try:
Checking the connection Checking the proxy, firewall, and DNS configuration Running Windows Network Diagnostics ERR_NAME_NOT_RESOLVED
http://wfr.tcl-lang.org/ https://login.attwifi.com/blocked/blocked_page.html#?......&web_rep=%3Ctrustworthy-sites%3E&web_cat=%3Cshareware-and-freeware%3E
Hi,
7/16/2020. ActiveState hasn't hosted the Tcler's Wiki for a while. From what I see in that error message though, it looks like the ATT network has DNS entries that still point to tcl.activestate.com, whereas the other providers are using the official URL instead.
We might have had a redirect sending tcl.activestate.com to the new official URL, and that redirect might have gone out of service. I have asked our IT team to investigate.
Best regards,
GS. ActiveState Software
NEW! ActiveState Platform: Build - Certify - Resolve Login to get your ActivePerl/Python/Tcl builds: https://platform.activestate.com/ .
gold 7/16/2020, end of file
# pseudocode on Babylonian triplets
2m, m**2 - 1, m**2 + 1 Babylonian triplet
twin prime number.
twin prime numbers separated by 2,4,6 ...?
c**2= a**2 + b**2
c**2= a**2 + 1 normalized Babylonian triplet
a**2 = c**2 -1 normalized Babylonian triplet
some b and c are both primes.
some b and c are not both primes.
The reciprocal pair relationship.
(X+1/X)**2 - (X+1/X)**2 = 4 , divide equation by 4
normalized triplet, < (1/4)* ((X+1/X)**2 ) , 1 ,(1/4)* ((X+1/X)**2) >
0 < X-1/X < 2
1< X-1/X < 1+sqrt(2) ~~ approximate limit of 2.4
The Babylonian regular numbers between 0 and 60 have a limited set of triplets that
satisfy 1< X-1/X < 1+sqrt(2) which appears to be the role of Plimpton 322.
The limit 1< X-1/X < 1+sqrt(2) may explain the 1<X<2 limit on the Late Babylonian
many place reciprocal tablets.
d=6 even number, l = divisor of d**2 with integer result, Babylonian triplet method
a=l+b
b= d+ (d**2)//(2*l)
c= d+l+(d**2)/(2*l)
# supposed to work for all even dPossible Bias of base 2 and 3 in near field?
New report indicates that binary numbers and base 3 may a bit biased in the near field. But don't think the sample is large enough in this trial program.
# Pretty print version from autoindent
# and ased editor
# Possible Bias of base 2 and 3 in near field?
# written on Windows 10 on TCL
# working under TCL version 8.6
# on TCL Club , 18aug2020
# relative frequency of indiv. "throw" over all "throws".
# pi mantissa used here
# proc base and frombase by RS
package require Tk
console show
# proc base by RS
proc base {base number} {
set negative [regexp ^-(.+) $number -> number] ;# (1)
set digits {0 1 2 3 4 5 6 7 8 9 A B C D E F G H I J K L M N
O P Q R S T U V W X Y Z a b c d e f g h i j k l m n o p
q r s t u v w x y z}
set res {}
while {$number} {
set digit [expr {$number % $base}]
set res [lindex $digits $digit]$res
set number [expr {$number / $base}]
}
if $negative {set res -$res}
set res
}
# proc base by RS
proc frombase {base number} {
set digits {0 1 2 3 4 5 6 7 8 9 A B C D E F G H I J K L M N
O P Q R S T U V W X Y Z a b c d e f g h i j k l m n o p
q r s t u v w x y z}
set negative [regexp ^-(.+) $number -> number]
set res 0
foreach digit [split $number ""] {
set decimalvalue [lsearch $digits $digit]
if {$decimalvalue<0 || $decimalvalue >= $base} {
error "bad digit $decimalvalue for base $base"
}
set res [expr {$res*$base + $decimalvalue}]
}
if $negative {set res -$res}
set res
}
proc calculation { facen } {
# prob. subroutines for mimic sequence of bronze
# prob. is throw combos of eg. "7" over all possible throws
# set lister [split {14159265358979323846} ""]
# in base 3 10111100001122100002122202221020002210001
# in base 2 1100010001111111110100001101001100110010011101001101011111000110
set target [ base 3 14159265358979323846 ]
set lister [split { 1100010001111111110100001101001100110010011101001101011111000110 } ""]
set ee [llength $lister ]
set kk [ llength [ lsearch -all $lister $facen ] ]
set prob [ expr { ($kk*1.) / $ee } ]
return $prob
}
set limit 12
puts "%|table| printed in|TCL format |% "
puts "&| quantity| value| comment, if any|& "
for { set i 0 } { $i <= $limit } { incr i } {
lappend listxxx $i
lappend listxxx [ calculation $i ]
puts " &| $i | [ calculation $i ] | |&"
}
#end
puts " [ base 2 14159265358979323846 ] "| table | printed in | TCL format |
|---|---|---|
| quantity | value | comment, if any |
| 0 | 0.4461538461538462 | |
| 1 | 0.5384615384615384 | |
| 2 | 0.0 | |
| 12 | 0.0 | 1100010001111111110100001101001100110010011101001101011111000110 |
binary pi in 512 places. 11. 0010010000111111011010101000100010000101101000110000100011010011 0001001100011001100010100010111000000011011100000111001101000100 1010010000001001001110000010001000101001100111110011000111010000 0000100000101110111110101001100011101100010011100110110010001001 0100010100101000001000011110011000111000110100000001001101110111 1011111001010100011001101100111100110100111010010000110001101100 1100000010101100001010011011011111001001011111000101000011011101 0011111110000100110101011011010110110101010001110000100100010111
| table | printed in | TCL format |
|---|---|---|
| quantity | value | comment, if any |
| 0 | 0.5394990366088632 | binary pi in 510 digits |
| 1 | 0.44701348747591524 | |
| 2 | 0.0 |
- Unexpected biases in the distribution of consecutive primes
- Robert J. Lemke Oliver, Kannan Soundararajan ,Department of Mathematics, Stanford University
- The Last Digit of Prime Numbers - Numberphile on Youtube
- Lecture on “Rock, paper, scissors in probability, Tadashi Tokieda
- Hardy-Littlewood conjectures.
- MATHEMATICS SCIENCE, A new pattern in primes, Shubashree Desikan, Hindu Times
- en.wikipedia.org wiki search on Tadashi_Tokieda
- https://www.ncbi.nlm.nih.gov articles/PMC4978288/
- Distribution of the units digit of primes, C. M. Ko, National Central University
- www.wired.com tadashi-tokieda-finds-startling-objects-in-plain-sight/
Subroutine Template
# adapted from tcl-wiki Stats 2011-05-22, arithmetic mean [RLE]
#
# ::math::quantity_into_ratios --
#
# Return the division of quantity by two or more given ratios
#
# Arguments:
# val first value is quantity
# args other values are two or more given ratios
#
# Results: parts of quantity divided by ratios
#
proc ::math::quantity_into_ratios {quantity args} {
set sum 0.
set N [ expr { [ llength $args ] + 1 } ]
if { $N == 1 } { return 0 }
foreach val $args {
set sum [ expr { $sum + $val } ]
}
foreach val $args {
lappend answer [ expr { $quantity * ($val/$sum) } ]
}
set answer
}
#puts " ::math::quantity_into_ratios ( 84 2 2 2 ) answer 12.0 24.0 48.0 "
#puts " [ ::math::quantity_into_ratios 84 1 2 4 ] "
#puts " [ ::math::quantity_into_ratios 84 ] for (::math::quantity_into_ratios 84) returns zero "sqrt_sum_of_squares
# adapted from tcl-wiki Stats 2011-05-22, arithmetic mean [RLE]
#
# sqrt_sum_of_squares --
#
# Return the sqrt_sum_of_squares by one or more
#
# Arguments:
#
# args other values are one or more
#
# Results: sqrt_sum_of_squares
#
proc sqrt_sum_of_squares { args} {
set sum 0.
set N [ expr { [ llength $args ] + 1 } ]
if { $N == 1 } { return 0 }
foreach val $args {
set sum [ expr { $sum + $val*$val } ]
}
set answer [ expr { sqrt($sum) } ]
}
#puts " ::math::sqrt_sum_of_squares ( 2 2 2 ) answer [sqrt 12 ]
# 3.4641016151377544
#puts " [ ::math::sqrt_sum_of_squares 1 2 4 ] "
#puts " [ ::math::sqrt_sum_of_squares 2 ] for ( ) returns zero "
console show
console eval {.console config -bg palegreen}
console eval {.console config -font {fixed 20 bold}}
console eval {wm geometry . 40x20}
puts " sqrt_sum_of_squares 2 2 2 equals [ sqrt_sum_of_squares 2 2 2 ]"
puts " sqrt_sum_of_squares 1 1 1 equals [ sqrt_sum_of_squares 1 1 1 ]"
puts " sqrt_sum_of_squares 1 1 equals [ sqrt_sum_of_squares 1 1 ]"
puts " sqrt_sum_of_squares 1 equals [ sqrt_sum_of_squares 1 ]"
puts " sqrt_sum_of_squares 0 equals [ sqrt_sum_of_squares 0 ]"output for sqrt_sum_of_squares
sqrt_sum_of_squares 2 2 2 equals 3.4641016151377544 sqrt_sum_of_squares 1 1 1 equals 1.7320508075688772 sqrt_sum_of_squares 1 1 equals 1.4142135623730951 sqrt_sum_of_squares 1 equals 1.0 sqrt_sum_of_squares 0 equals 0.0
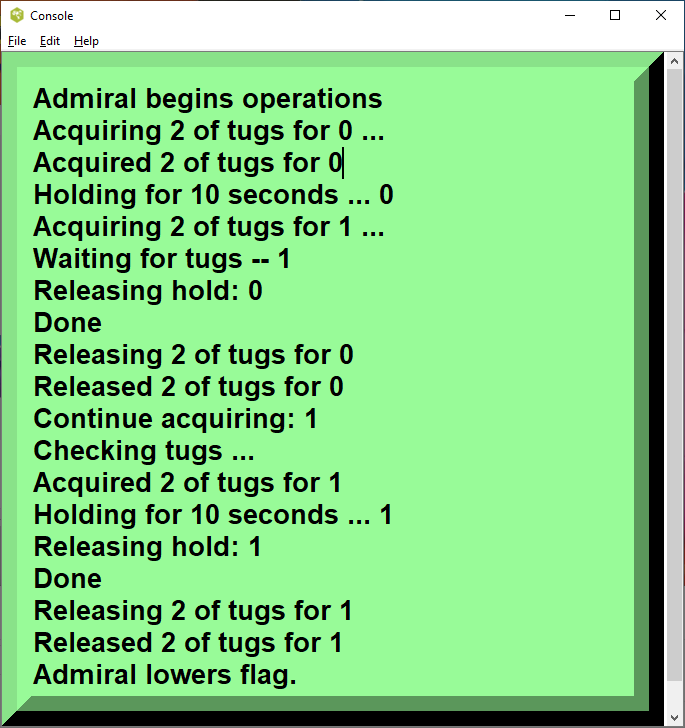
Modify discrete events on tugboats_tester3
From Discrete event modelling with coroutines by Author : Arjen Markus (21 april 2009). Added easy eye console for my bad eyes.
# coro_discrete_events.tcl --
# Experiment with SIMULA/DEMOS like modelling - using coroutines
# from Discrete event modelling with coroutines
# Author : Arjen Markus (21 april 2009)
# Discrete event modelling is a way of modelling all manner of systems
package require Tcl 8.6
# acquire --
# Acquire resources and wait if that does not succeed
#
# Arguments:
# name Name of the resource
# amount Amount to acquire
#
# Returns:
# None
#
# start modifications
package require math::numtheory
package require math::constants
package require math::trig
package require math
namespace path {::tcl::mathop ::tcl::mathfunc math::numtheory math::trig math::constants }
set tclprecision 17
console show
# following dresses up console output to easy eye
console eval {.console config -bg palegreen}
console eval {.console config -font {fixed 20 bold}}
console eval {wm geometry . 40x20}
console eval {.console config -background palegreen -highlightcolor tan -relief raised -border 30 }
# changes: shifted text, removed empty lines, added easy eye console to deck.
# changes: ran text through autoindent of ASED TCL editor
# end modifications
proc acquire {name amount} {
upvar 1 objectID ID
upvar #0 $name resource_name
puts "Acquiring $amount of $name for $ID ..."
if { $resource_name >= $amount } {
set resource_name [expr {$resource_name - $amount}]
} else {
puts "Waiting for $name -- $ID"
while {1} {
set ::queue($name) [linsert $::queue($name) 0 $ID]
yield [list acquire $name $ID]
puts "Checking $name ..."
if { $resource_name >= $amount } {
set resource_name [expr {$resource_name - $amount}]
break
}
puts "Wait again - $name - $resource_name -- $amount ..."
}
}
puts "Acquired $amount of $name for $ID"
}
# release --
# Release resources
#
# Arguments:
# name Name of the resource
# amount Amount to release
#
# Returns:
# None
#
proc release {name amount} {
upvar 1 objectID ID
upvar #0 $name resource_name
set resource_name [expr {$resource_name + $amount}]
puts "Releasing $amount of $name for $ID"
if { [llength $::queue($name)] != 0 } {
set hid [lindex $::queue($name) 0]
set ::queue($name) [lrange $::queue($name) 1 end]
set ::events [linsert $::events 0 [list $hid acquire 0.0]]
}
puts "Released $amount of $name for $ID"
}
# resource --
# Create a named resource
#
# Arguments:
# name Name of the resource
# amount Amount to create
#
# Returns:
# None
#
proc resource {name amount} {
upvar #0 $name resource_name
set resource_name $amount
set ::queue($name) {}
}
# hold --
# Advance the time for the given object in the simulation
#
# Arguments:
# delay Time to advance
#
# Returns:
# None
#
proc hold {delay} {
upvar 1 objectID object
lappend ::events [list $object "hold" [expr {$::time+$delay}]]
puts "Holding for $delay seconds ... $object"
yield
puts "Done"
}
# object --
# Create an object and schedule it's coming alive
#
# Arguments:
# procedure Name of the procedure holding the life cycle
# time Time at which it comes alive
#
# Returns:
# Structure representing the object
#
proc object {procedure time} {
set obj [list $procedure $::objectno]
lappend ::events [list $obj "init" $time]
incr ::objectno
return $obj
}
# handleEvents --
# Handle the events that were scheduled
#
# Arguments:
# None
#
# Returns:
# None
#
proc handleEvents {} {
global time
global events
while { [llength $events] > 0 } {
set count 0
set found 0
foreach event $events {
foreach {obj type eventTime} $event {break}
if { $eventTime <= $time } {
set events [lreplace $events $count $count]
set found 1
break
}
incr count
}
if { ! $found } {
foreach {obj type eventTime} [lindex $events 0] {break}
set events [lrange $events 1 end]
}
if { $time < $eventTime } {
set time $eventTime
}
if { $type == "init" } {
coroutine [lindex $obj 1] {*}$obj
}
if { $type == "hold" } {
puts "Releasing hold: $obj"
$obj
}
if { $type == "acquire" } {
puts "Continue acquiring: $obj"
$obj
}
}
}
# startSimulation --
# Start the simulation
#
# Arguments:
# None
#
# Returns:
# None
#
proc startSimulation {} {
if { [llength $::events] == 0 } {
return
} else {
handleEvents
}
}
# boat --
# Simulate a boat that requires several tugs to get into the harbour
#
# Arguments:
# objectID ID of the object (required name!)
#
# Returns:
# None
#
proc boat {objectID} {
acquire tugs 2
hold 10
release tugs 2
}
# main --
# Simulate two objects that need the same resources
#
# Initialise simulation system
set objectno 0
set time 0.0
set events {}
# The simulation itself
resource tugs 3
set b1 [object boat 1.0]
set b2 [object boat 4.0]
startSimulationgold 9/10/2020. added pix.
Equivalent One Liners V2
Beginning in the sixties, the one liner program was typed input to the command line of an operating computer system terminal so that the one line command performs some useful function in a single one line of terminal input. Some of the original one liner commands were limited to a 60 character display on especially the early Basic terminals or to a 72 characters on the Fortran punched cards. Of course, the hit return to send, terminal flashing bulbs, and automatic answer back were silently understood as part or supporting the one liner program. Some of the line lengths in some computer languages were later extended to 410 lines and so on. The definition and use of the one liner program has been widened to include program source for any language that does something useful in one line. On batch programs, controlling and setting variable statements like RETURN, STOP, END, extra terminal prompts, and setting initial variables were used in Fortran systems. Of course, a very good feature of TCL is that new variables as number types do not have to be initialized prior to use and no subroutine RETURN and END statements are necessary, vis the older Fortran and Basic dogmas in moldy textbooks. Repeating, setting a new number variable to 0 or 1 is not necessary prior to using the variable. Since a partial and practical goal of computer programming is to produce human readable code, it is permissible on the published console batch programs here to retain some vestigial stages to aid human comprehension.
Timing Equivalent One Liners V2
# pretty print from autoindent and ased editor
# Timing Equivalent One Liners V2
# written on Windows 10 on eTCL
# working under TCL version 8.6
# gold on TCL Club , 8/20/2020
# Ref. WIKI BOOKS, Tcl_Programming_Introduction
# Book Section contrasts one liners
# versus traditional procedural approach
# below contains redundant procs
package require Tk
package require math::numtheory
package require math::constants
package require math::trig
package require math
namespace path {::tcl::mathop ::tcl::mathfunc math::numtheory math::trig math::constants }
set tcl_precision 17
proc pie {} {return [expr acos(-1)]}
console show
console eval {.console config -bg palegreen}
console eval {.console config -font {fixed 20 bold}}
console eval {wm geometry . 40x20}
# uses join, but computer time on some?
proc mean_1 list {expr double([join $list +])/[llength $list]}
# math operators exposed as commands, and the expand operator
proc mean_2 list {expr {[tcl::mathop::+ {*}$list]/double([llength $list])}}
# import the tcl::mathop operators
proc mean_3 list {expr {[+ {*}$list]/double([llength $list])}}
# import the tcl::mathop operators from <Summing a list>
# list add ladd or summing a list
proc ladd_1 {listx} {::tcl::mathop::+ {*}$listx}
# using join in ladd_2 from RS
proc ladd_2 {listx} {expr [join $listx +]+0} ;# RS
# using expr including non integers from PYK 2016-04-13
proc ladd_3 {listx} {set total 0.0; foreach nxt $listx {set total [expr {$total + $nxt}]}; return $total}
set limit 12
puts "%|table| | printed in|TCL format |% "
puts "&| session| proc & mean value| elements in list | comment, if any|& "
for { set i 0 } { $i <= $limit } { incr i } {
set lister { 1 2 4 5 6 7 8 9 10 }
lappend lister [* $i [pie]]
puts "&|$i | ladd_1 [ ladd_1 $lister ] | $lister | proc timer [ time { set qq [ ladd_1 $lister ]} 5000 ] |&"
puts "&|$i | ladd_2 [ ladd_2 $lister ] | $lister | proc timer [ time { set qq [ ladd_2 $lister ]} 5000 ] |&"
puts "&|$i | ladd_3 [ ladd_3 $lister ] | $lister | proc timer [ time { set qq [ ladd_3 $lister ]} 5000 ] |&"
puts "&|$i | mean_1 [ mean_1 $lister ] | $lister | proc timer [ time { set qq [ mean_1 $lister ]} 5000 ] |&"
puts "&|$i | mean_2 [ mean_2 $lister ] | $lister | proc timer [ time { set qq [ mean_2 $lister ]} 5000 ] |&"
puts "&|$i | mean_3 [ mean_3 $lister ] | $lister | proc timer [ time { set qq [ mean_3 $lister ]} 5000 ] |&"
puts "&|$i | ::math::mean [::math::mean 1 2 4 5 6 7 8 9 10 [* $i [pie]]] | $lister | proc timer [ time { set qq [ ::math::mean 1 2 4 5 6 7 8 9 10 [* $i [pie]] 5000 ]} ] |&"
}
#end Table of Timing 4 Procs
| table | printed in | TCL format | |
|---|---|---|---|
| session | proc & mean value | elements in list | comment, if any |
| 0 | ladd_1 52.0 | 1 2 4 5 6 7 8 9 10 0.0 | proc timer 2.3273999999999999 microseconds per iteration |
| 0 | ladd_2 52.0 | 1 2 4 5 6 7 8 9 10 0.0 | proc timer 5.6311999999999998 microseconds per iteration |
| 0 | ladd_3 52.0 | 1 2 4 5 6 7 8 9 10 0.0 | proc timer 4.3941999999999997 microseconds per iteration |
| 0 | mean_1 5.2000000000000002 | 1 2 4 5 6 7 8 9 10 0.0 | proc timer 13.053599999999999 microseconds per iteration |
| 0 | mean_2 5.2000000000000002 | 1 2 4 5 6 7 8 9 10 0.0 | proc timer 3.0369999999999999 microseconds per iteration |
| 0 | mean_3 5.2000000000000002 | 1 2 4 5 6 7 8 9 10 0.0 | proc timer 2.3805999999999998 microseconds per iteration |
| 0 | ::math::mean 5.2000000000000002 | 1 2 4 5 6 7 8 9 10 0.0 | proc timer 22 microseconds per iteration |
| 1 | ladd_1 55.141592653589797 | 1 2 4 5 6 7 8 9 10 3.1415926535897931 | proc timer 1.7847999999999999 microseconds per iteration |
| 1 | ladd_2 55.141592653589797 | 1 2 4 5 6 7 8 9 10 3.1415926535897931 | proc timer 7.3037999999999998 microseconds per iteration |
| 1 | ladd_3 55.141592653589797 | 1 2 4 5 6 7 8 9 10 3.1415926535897931 | proc timer 1.7285999999999999 microseconds per iteration |
| 1 | mean_1 5.5141592653589795 | 1 2 4 5 6 7 8 9 10 3.1415926535897931 | proc timer 8.3374000000000006 microseconds per iteration |
| 1 | mean_2 5.5141592653589795 | 1 2 4 5 6 7 8 9 10 3.1415926535897931 | proc timer 2.2898000000000001 microseconds per iteration |
| 1 | mean_3 5.5141592653589795 | 1 2 4 5 6 7 8 9 10 3.1415926535897931 | proc timer 2.1674000000000002 microseconds per iteration |
| 1 | ::math::mean 5.5141592653589795 | 1 2 4 5 6 7 8 9 10 3.1415926535897931 | proc timer 6 microseconds per iteration |
| 2 | ladd_1 58.283185307179586 | 1 2 4 5 6 7 8 9 10 6.2831853071795862 | proc timer 1.7618 microseconds per iteration |
| 2 | ladd_2 58.283185307179586 | 1 2 4 5 6 7 8 9 10 6.2831853071795862 | proc timer 6.6627999999999998 microseconds per iteration |
| 2 | ladd_3 58.283185307179586 | 1 2 4 5 6 7 8 9 10 6.2831853071795862 | proc timer 4.0709999999999997 microseconds per iteration |
| 2 | mean_1 5.8283185307179588 | 1 2 4 5 6 7 8 9 10 6.2831853071795862 | proc timer 8.5307999999999993 microseconds per iteration |
| 2 | mean_2 5.8283185307179588 | 1 2 4 5 6 7 8 9 10 6.2831853071795862 | proc timer 2.1261999999999999 microseconds per iteration |
| 2 | mean_3 5.8283185307179588 | 1 2 4 5 6 7 8 9 10 6.2831853071795862 | proc timer 2.3512 microseconds per iteration |
| 2 | ::math::mean 5.8283185307179588 | 1 2 4 5 6 7 8 9 10 6.2831853071795862 | proc timer 5 microseconds per iteration |
| 3 | ladd_1 61.424777960769376 | 1 2 4 5 6 7 8 9 10 9.4247779607693793 | proc timer 1.9702 microseconds per iteration |
| 3 | ladd_2 61.424777960769376 | 1 2 4 5 6 7 8 9 10 9.4247779607693793 | proc timer 7.1285999999999996 microseconds per iteration |
| 3 | ladd_3 61.424777960769376 | 1 2 4 5 6 7 8 9 10 9.4247779607693793 | proc timer 2.6114000000000002 microseconds per iteration |
| 3 | mean_1 6.1424777960769372 | 1 2 4 5 6 7 8 9 10 9.4247779607693793 | proc timer 8.5581999999999994 microseconds per iteration |
| 3 | mean_2 6.1424777960769372 | 1 2 4 5 6 7 8 9 10 9.4247779607693793 | proc timer 2.1989999999999998 microseconds per iteration |
| 3 | mean_3 6.1424777960769372 | 1 2 4 5 6 7 8 9 10 9.4247779607693793 | proc timer 2.4533999999999998 microseconds per iteration |
| 3 | ::math::mean 6.1424777960769372 | 1 2 4 5 6 7 8 9 10 9.4247779607693793 | proc timer 5 microseconds per iteration |
| 4 | ladd_1 64.566370614359172 | 1 2 4 5 6 7 8 9 10 12.566370614359172 | proc timer 1.7842 microseconds per iteration |
| 4 | ladd_2 64.566370614359172 | 1 2 4 5 6 7 8 9 10 12.566370614359172 | proc timer 10.103400000000001 microseconds per iteration |
| 4 | ladd_3 64.566370614359172 | 1 2 4 5 6 7 8 9 10 12.566370614359172 | proc timer 1.9608000000000001 microseconds per iteration |
| 4 | mean_1 6.4566370614359174 | 1 2 4 5 6 7 8 9 10 12.566370614359172 | proc timer 8.8523999999999994 microseconds per iteration |
| 4 | mean_2 6.4566370614359174 | 1 2 4 5 6 7 8 9 10 12.566370614359172 | proc timer 2.0948000000000002 microseconds per iteration |
| 4 | mean_3 6.4566370614359174 | 1 2 4 5 6 7 8 9 10 12.566370614359172 | proc timer 2.2736000000000001 microseconds per iteration |
| 4 | ::math::mean 6.4566370614359174 | 1 2 4 5 6 7 8 9 10 12.566370614359172 | proc timer 5 microseconds per iteration |
| 5 | ladd_1 67.707963267948969 | 1 2 4 5 6 7 8 9 10 15.707963267948966 | proc timer 3.6421999999999999 microseconds per iteration |
| 5 | ladd_2 67.707963267948969 | 1 2 4 5 6 7 8 9 10 15.707963267948966 | proc timer 10.6218 microseconds per iteration |
| 5 | ladd_3 67.707963267948969 | 1 2 4 5 6 7 8 9 10 15.707963267948966 | proc timer 2.3553999999999999 microseconds per iteration |
| 5 | mean_1 6.7707963267948967 | 1 2 4 5 6 7 8 9 10 15.707963267948966 | proc timer 8.4225999999999992 microseconds per iteration |
| 5 | mean_2 6.7707963267948967 | 1 2 4 5 6 7 8 9 10 15.707963267948966 | proc timer 2.1343999999999999 microseconds per iteration |
| 5 | mean_3 6.7707963267948967 | 1 2 4 5 6 7 8 9 10 15.707963267948966 | proc timer 2.1093999999999999 microseconds per iteration |
| 5 | ::math::mean 6.7707963267948967 | 1 2 4 5 6 7 8 9 10 15.707963267948966 | proc timer 5 microseconds per iteration |
bits and pieces, Testing One Liner Programs
set strinit “123456789”
proc string_end strin5 { string index $strin5 end}
string_end $strinit
# out 9
proc sea5 bb { set i 2;if {$i < 10} { while {$i < 5} { puts [incr i]}}}
sea 5
# return first character of string
proc string_end5 bb { string index $bb 0 }
# return last character of string
proc string_end5 bb { string index $bb end }
# Enter number num for next above power of 2, John K. Ousterhout, Tcl and the Tk Toolkit
proc near_above_power_of_2 num {set pow 1; while {$pow<$num} {set pow [expr { $pow*2} ]}; return $pow}
# Usage near_above_power_of_2 7 returns 8,
# Usage near_above_power_of_2 9 returns 16,
# Usage near_above_power_of_2 99999999999999 140737488355328
# Enter number num for next below power of 2, John K. Ousterhout, Tcl and the Tk Toolkit
proc near_below_power_of_2 num {set pow 1; while {$pow< [expr {$num - 1}] } {set pow [expr { $pow*2} ]}; return [expr { $pow*.5} ]}
# Usage near_below_power_of_2 7 returns 4. # start advice file.
AMG: The return value of a Tcl procedure is inherited from the return value of the last command to execute within that procedure. Therefore, many uses of the [return] command are redundant. For example, this procedure:
proc anglecosa {a b c} {return [expr {($b*$b+$c*$c-$a*$a)/(2.*$b*$c)}]}
can be written more simply:
proc anglecosa {a b c} {expr {($b*$b+$c*$c-$a*$a)/(2.*$b*$c)}}
Also, the conditional arguments to [if], [while], [for] are already expr-essions, so there's no need to nest a call to [expr]. For example,
proc emmy2 {} {if {[expr {rand()}] <= 0.9} {return 1}}
can be simplified quite a lot:
proc emmy2 {} {if {rand() <= 0.9} {return 1}}
#end of advice filescratch
proc near_above_power_of_2x num {set pow 1; while {$pow<$num} {set pow [expr { $pow*2} ]}; return $pow}
proc near_above_power_of_2 num {set pow 1; while {$pow<$num} {set pow [expr { $pow*2} ]}; return $pow}
proc ld x "expr {log(\$x)/[expr log(2)]}" ;# RS
[pow 2 [+ [int 2.8] 1]]= "8.0"
proc zap x "[pow 2 [+ 1 [expr {log(\$x)/[expr log(2)]}]"
proc zap x "pow 2 [+ [int 2.8] 1]"One Liners from www.codecodex.com/wiki
#under test from www.codecodex.com/wiki
set lister { 1 2 4 5 6 7 8 9 10 }
set s {starchild}
package require struct::list
proc reverseWords s {return [struct::list reverse [split $s]]}
proc ! n {expr {$n<2? 1: $n*[! [incr n -1]]}}
# usage ! 5 returns 120
proc average list {expr ([join $list +])/[llength $list].}
for {set i 1} {$i <= 1000} {incr i} {pust [expr {$i*($i+1)/2}]}
namespace import ::tcl::mathop::*
proc average list {expr {[+ {*}$list]/double([llength $list])}}
# works here , average $lister returns 5.777777777777778
proc fib n {expr {$n<2? $n: [fib [incr n -1]] + [fib [incr n -1]]}}
# not working here
namespace import ::tcl::mathfunc::*
::tcl::mathfunc::isqrt 26
# ::tcl::mathfunc::isqrt 26 returns 5, working here
set date [clock format [clock scan $date] -format {%Y-%m-%d %H:%M:%S}] ;#dclaar
scriptEval clock format [clock scan $tDate] -format {%Y-%m-%d %H:%M:%S} ;#dclaar
# clock scan is your friend; it knows all sorts of formats. In
# case above, it converts: Oct 15 06:52:45 2009 to: 2009-10-15 06:52:45Testing One Liner Program for list_twin_primes V2
# pretty print from autoindent and ased editor
# list_twin_primes V2
# written on Windows 10 on TCL
# working under TCL version 8.6
# gold on TCL Club , 8/20/2020
# Ref. WIKI BOOKS, Tcl_Programming_Introduction
# Book Section contrasts one liners
# versus traditional procedural approach
# below contains redundant procs
package require Tk
package require math::numtheory
package require math::constants
package require math::trig
package require math
namespace path {::tcl::mathop ::tcl::mathfunc math::numtheory math::trig math::constants }
set tcl_precision 17
proc pie {} {return [expr acos(-1)]}
console show
console eval {.console config -bg palegreen}
console eval {.console config -font {fixed 20 bold}}
console eval {wm geometry . 40x20}
# invoking TCLLIB math::numtheory
proc isprimex x {expr {$x>1 && ![regexp {^(oo+?)\1+$} [string repeat o $x]]}}
# list_twin_primes proc under test, list_twin_primes and isprime procs are recursion limited
proc list_twin_primesx { aa bb cc} { for {set i $aa} {$i<=$bb} {incr i $cc} { if {[isprime $i] && [isprime [+ $i $cc ]] } {lappend boo $i [+ $i $cc ] } } ; return $boo}
proc list_twin_primes { aa bb cc} { for {set i $aa} {$i<=$bb} {incr i 1} { if {[isprime $i] && [isprime [+ $i $cc ] ] } { lappend boo $i [+ $i $cc ] } } ; return $boo}
# aa is start number, bb is upper limit, cc is separator number, usually even 2
# The original Dickson conjecture has separator even numbers 2,4,6 ... ?
# list_twin_primes 0 25 2 returns 3 5 5 7 11 13 17 19
# The sets <13 15> and <15 17> are separated by a even 2,
# but left out of answer.
# Note the 15 is not a prime number and has factors <3 5>.
# The set <13 17> has two primes, but separated by an even 4.
# reference On-Line Encyclopedia of Integer Sequences website
# OEIS A077800 discussed that the twin prime sets <p,p+2> are
# (3, 5), (5, 7), (11, 13), (17, 19),
# (29, 31), (41, 43), (59, 61), (71, 73),
# (101, 103), (107, 109), (137, 139)...
# OEIS A275021 has samples of <p,p+4> and omits pairs of <p,p+2>
# 79, 83, 127, 131, 163, 167, 379, 383, 397, 401, 439, 443,...
# list_twin_primes 75 135 4 returns 79 83 103 107 127 131
# reference On-Line Encyclopedia of Integer Sequences website
# OEIS A023201 has some samples of <p,p+6>
# 5, 7, 11, 13, 17, 23, 31, 37,
# 41, 47, 53, 61, 67, 73, 83, 97, 101
# contains redundant procs for testing
puts "[list_twin_primes 3 25 2 ]"
puts "[list_twin_primes 3 25 4 ]"
puts "[list_twin_primes 3 25 6 ]"Table Results on Twin Primes for 2,4,6,10 Separators
| table | Twin Primes for 2,4,6,10 Separators | printed in | TCL format | |
|---|---|---|---|---|
| result | lower limit | upper limit | separator integer | comment, if any |
| elements in list | lower limit | upper limit | separator integer | comment, if any |
| 3 5 5 7 11 13 17 19 | 3 | 25 | 2 | |
| 3 7 7 11 13 17 19 23 | 3 | 25 | 4 | |
| 5 11 7 13 11 17 13 19 17 23 23 29 | 3 | 25 | 6 | |
| 3 13 7 17 13 23 19 29 | 3 | 25 | 10 |
Older TCL4 reserve
gold Here are some one line procedures for circle area and law of cosines. See tcl::mathfunc cos pi constants Functions ::math::constants::constants and ::math::fibonacci are available in the TCLLIB.
proc pi {} {expr {acos(-1)}} #from AMG see below
proc degtoradiansconst {} {return [ expr {180./[pi]} ]}
proc degz {} {return [ expr {180./[pi]} ]}
proc degx {aa} {return [ expr { [degz]*acos($aa) } ]}
proc inrad {a b c} {return [expr {(sqrt(($a+$b+$c)*($a+$b-$c)*($a-$b+$c)*($b+$c-$a)))/(2.*($a+$b+$c)) } ] }
proc circlediameter {radius} { return [ expr { 2.* $radius } ] }
proc circlearea {radius} { return [ expr { [pi]*($radius**2) }]}
proc circlecircumference {radius} {return [ expr {2.*[pi]*$radius }]}
proc spherediameter {radius} {return [ expr { 2.* $radius }]}
proc spherevolume {radius} { return [ expr { (4./3.)*[pi]*($radius**3) }]}
proc spheresurface {radius} { return [ expr { 4.*[pi]*($radius**3) }]}
proc cubevolume {aa} { return [ expr { 1.*$aa*$aa*$aa } ] }
proc squarearea {aa} { return [ expr { 1.*$aa*$aa } ] }
proc ellipsoidvolume {aa bb cc} { return [ expr { 1.*(4./3.)*[pi]*$aa*$bb*$cc } ] }
proc ellipsearea1 { aa bb } {return [ expr { 1.*[pi]*$aa*$bb } ]}
proc ellipseperimeterx {aa bb} { set tt [ expr { ($aa*$aa+$bb*$bb)/2.}];return [ expr { 2.*[pi]*sqrt($tt)} ] }
proc spherevolumex {aa } { return [ expr { 1.*(4./3.)*[pi]*$aa*$aa*$aa } ] }
proc spheroidvolumex {aa cc } { return [ expr { 1.*(4./3.)*[pi]*$aa*$aa*$cc } ] }
proc torusvolumex {aa bb } { return [ expr {(1./4.) *[pi]*[pi] * ($aa + $bb) * ($aa - $bb)*2.}] }
proc torussurfacex {aa bb } { return [ expr { [pi]*[pi] * ($aa*$aa - $bb*$bb) }] }
proc conesurfacex {aa rr } { return [ expr { [pi]*$rr*$aa}] }
proc cylindersurfacesidex {aa rr } { return [ expr {2.* [pi]*$rr*$aa}] }
proc cylinderwholesurfacesidex {aa rr } { return [ expr {2.* [pi]*$rr*$aa +2.*[pi]*$rr*$rr}] }
proc cylindervolumesidex {aa rr } { return [ expr { [pi]*$rr*$rr*$aa}] }
proc conevolumex {aa rr } { return [ expr { (1./3.)*[pi]*$rr*$rr*$aa}] }
proc pyramidvolumex {aa bb cc } { return [ expr { (1./3.)*$aa*$bb*$cc }] }
proc rectangularprismvolumex {aa bb cc } { return [ expr { $aa*$bb*$cc }] }
proc triangularprismvolumex {aa bb cc } { return [ expr { $aa*$bb*$cc*.5 }] }
proc polygonperimeterx {aa bb } { return [ expr { $aa*$bb}] }
proc rectangleperimeterx {aa bb } { return [ expr {2.*( $aa+$bb)}] }
proc parallelogramperimeterx {aa bb } { return [ expr {2.*( $aa+$bb)}] }
proc triangleperimeterx {aa bb cc} { return [ expr { $aa+$bb+$cc }] }
proc triangletrapezoidx {aa bb cc} { return [ expr { $aa*($bb+$cc)*(1./2.) }] }
#law of cosines, aa bb cc are three sides of right triangle, here ordered
#as aa small side , bb middle side, cc largest side.
# inrad is radius of cirle inscribed in right triangle,
# use sides as inrad aa bb cc
proc anglecosa { aa bb cc } {return [ expr { ($bb*$bb+$cc*$cc-$aa*$aa)/(2.*$bb*$cc) }]}
proc anglecosb { aa bb cc } {return [ expr { ($cc*$cc+$aa*$aa-$bb*$bb)/(2.*$aa*$cc) }]}
proc anglecosc { aa bb cc } { return [ expr { ($aa*$aa+$bb*$bb-$cc*$cc)/(2.*$aa*$bb) }]}
#with examples
#for radius of 1
#circlediameter 1
#circlearea 1
#circlecircumference 1
#spherediameter 1
#spherevolume 1
#spheresurface 1
#inrad 3 4 5
#anglecosa 3 4 5
#anglecosb 3 4 5
#anglecosc 3 4 5
# following include redundant TCL one liner procedures for sqrt of sum of squares
# sqrt of sum of squares and diagonal using expr
proc diagonal_1 {aa bb} {[expr { sqrt($aa * $aa + $bb * $bb)}] }
# Usage diagonal 1 1 returns 1.4142135623730951
# diagonal using math ops
proc diagonal_2 {aa bb} {[sqrt [+ [* $aa $aa] [* $bb $bb] ] ]}
# Usage diagonal_2 1 1 returns 1.4142135623730951
# diagonal using math hypot function
proc diagonal_3{aa bb} {[ hypot $aa $bb ]}
# Usage diagonal_3 1 1 returns 1.4142135623730951
# time one liners, but sticking >> [ time { set qq [ diagonal_1 1 1 ] } ]
proc diagonal_1x {aa bb} { [ time [sqrt [+ [* $aa $aa] [* $bb $bb] ] ]]}Sample of TCL One Liner Procedures V2
# Sample of TCL One Liner Procedures V2
# written on Windows 10 on TCL 8.6
# working under TCL version 8.6
# gold on TCL Club , 9/20/2020
# Ref. WIKI BOOKS, Tcl_Programming_Introduction pdf
# Book Section contrasts one liners procedures
# versus traditional procedural approach.
# Below contains redundant One Liner procedures
# to contrast alternate techniques and constructs
# start modifications
package require Tcl 8.6
package require math::numtheory
package require math::constants
package require math::trig
package require math
namespace path {::tcl::mathop ::tcl::mathfunc math::numtheory math::trig math::constants }
set tclprecision 17
console show
# following dresses up console output to easy eye
console eval {.console config -bg palegreen}
console eval {.console config -font {fixed 20 bold}}
console eval {wm geometry . 40x20}
puts "Admiral begins operations "
# changes: shifted text, removed empty lines, added easy eye console to deck.
# end modifications
console show
console eval {.console config -bg palegreen}
console eval {.console config -font {fixed 20 bold}}
console eval {wm geometry . 40x20}
namespace path {::tcl::mathop ::tcl::mathfunc}
# contains redundant procs for testing one liner procedures V2
proc pi {} {expr {acos(-1)}}
# proc pi from AMG see below
proc degtoradiansconst {} { expr {180./ [pi] }}
proc degz {} { expr {180./ [pi] }}
proc degx {aa} { expr { degz *acos($aa)}}
proc inrad {a b c} { expr {(sqrt(($a+$b+$c)*($a+$b-$c)*($a-$b+$c)*($b+$c-$a)))/(2.*($a+$b+$c))}}
proc circlediameter {radius} { expr { 2.* $radius }}
proc circlearea {radius} { expr { [pi] *($radius**2)}}
proc circlecircumference {radius} { expr {2.* [pi] *$radius }}
proc spherediameter {radius} { expr { 2.* $radius }}
proc spherevolume {radius} { expr { (4./3.)* [pi] *($radius**3)}}
proc spheresurface {radius} { expr { 4.* [pi] *($radius**3)}}
proc cubevolume {aa} { expr { 1.*$aa*$aa*$aa }}
proc squarearea {aa} { expr { 1.*$aa*$aa }}
proc ellipsoidvolume {aa bb cc} { expr { 1.*(4./3.)* [pi] *$aa*$bb*$cc }}
proc ellipsearea1 { aa bb } { expr { 1.* [pi] *$aa*$bb }}
proc ellipseperimeterx {aa bb} { set tt [ expr { ($aa*$aa+$bb*$bb)/2.}];return [ expr { 2.*[pi]*sqrt($tt)} ] }
proc spherevolumex {aa } { expr { 1.*(4./3.)* [pi] *$aa*$aa*$aa }}
proc spheroidvolumex {aa cc } { expr { 1.*(4./3.)* [pi] *$aa*$aa*$cc }}
proc torusvolumex {aa bb } { expr {(1./4.) * [pi] * [pi] * ($aa + $bb) * ($aa - $bb)*2.}}
proc torussurfacex {aa bb } { expr { [pi] * [pi] * ($aa*$aa - $bb*$bb)}}
proc conesurfacex {aa rr } { expr { [pi] *$rr*$aa}}
proc cylindersurfacesidex {aa rr } { expr {2.* [pi] *$rr*$aa}}
proc cylinderwholesurfacesidex {aa rr } { expr {2.* [pi] *$rr*$aa +2.* [pi] *$rr*$rr}}
proc cylindervolumesidex {aa rr } { expr { [pi] *$rr*$rr*$aa}}
proc conevolumex {aa rr } { expr { (1./3.)* [pi] *$rr*$rr*$aa}}
proc pyramidvolumex {aa bb cc } { expr {(1./3.)*$aa*$bb*$cc }}
proc rectangularprismvolumex {aa bb cc } { expr { $aa*$bb*$cc }}
proc triangularprismvolumex {aa bb cc } { expr { $aa*$bb*$cc*.5 }}
proc polygonperimeterx {aa bb } { expr { $aa*$bb}}
proc rectangleperimeterx {aa bb } { expr {2.*( $aa+$bb)}}
proc parallelogramperimeterx {aa bb } { expr {2.*( $aa+$bb)}}
proc triangleperimeterx {aa bb cc} { expr { $aa+$bb+$cc }}
proc triangletrapezoidx {aa bb cc} { expr { $aa*($bb+$cc)*(1./2.)}}
#law of cosines, aa bb cc are three sides of right triangle, here ordered
#as aa small side , bb middle side, cc largest side.
# inrad is radius of cirle inscribed in right triangle,
# use sides as inrad aa bb cc
proc anglecosa { aa bb cc } { expr {($bb*$bb+$cc*$cc-$aa*$aa)/(2.*$bb*$cc)}}
proc anglecosb { aa bb cc } { expr {($cc*$cc+$aa*$aa-$bb*$bb)/(2.*$aa*$cc)}}
proc anglecosc { aa bb cc } { expr {($aa*$aa+$bb*$bb-$cc*$cc)/(2.*$aa*$bb)}}
#with examples
#for radius of 1
#circlediameter 1
#circlearea 1
#circlecircumference 1
#spherediameter 1
#spherevolume 1
#spheresurface 1
#inrad 3 4 5
#anglecosa 3 4 5
#anglecosb 3 4 5
#anglecosc 3 4 5
# following include redundant TCL one liner procedures for sqrt of sum of squares
# sqrt of sum of squares and diagonal using expr
proc diagonal_1 {aa bb} { expr { sqrt($aa * $aa + $bb * $bb)}}
# Usage diagonal 1 1 s 1.4142135623730951
# maturity value of loan using TCL 8.6 math ops, 10Sep2020
# similar formula for time in days divide years by 360.
# similar formula for interest rate in percent, divide interest by 100.
# should work with any currency and just use consistent units.
# maintain isolating spaces in TCL math ops
proc maturity_value_loan { principal interest years} { [* $principal [+ 1. [* 1. $interest $years ]]] }
# Usage maturity_value_loan 100. .05 1. returns 105.
proc maturity_value_loan_percent { principal percent_i years} { [* $principal [+ 1. [* 1. [/ $percent_i 100.] $years ]]] }
# Usage maturity_value_loan_percent 100. 5. 1. returns 105.
proc maturity_value_loan_days { principal interest days} { [* $principal [+ 1. [* 1. $interest [/ $days 360. ]]]] }
# Usage maturity_value_loan_days 100. .05 360. returns 105.
# following proc session invoke TCLLIB math::trig library
proc pyramid_d {hh bb} { [ acotand [expr (.5*$bb/$hh) ]] }
proc pyra_d {hh bb} { [ acotand [* .5 [/ $bb $hh] ]] }
# Usage pyramid_degrees 57.692 106.346 answer 47.334157521261254
# hh is height of pyramid, units cancel out
# bb is base length of pyramid
# seked = (7 * .5 * 360 cubits) / 250 cubits = 5.04 decimal palms
proc seked_d {hh bb} { [/ [* 7. .5 $bb ] $hh ] }
# usage seked_d 250. 360. equals 5.04
# end TCLLIB
# hbA1c_convert_to_average_blood_glucose mg/dl HbA1c
proc a1c hbA1c { expr { 35.6*$hbA1c -77.3} }
# convert mg/dl to mmol/L average blood glucose
# some papers round off 18.016 to mgdl/18.
proc mgdl_to_mmoll mgdl { expr { $mgdl/18.0 } }
# convert mmol/L to mg/dl average blood glucose
proc mmoll_to_mgdl mmoll { expr { $mmoll*18.0 } }
# *************************************8
# mean_speed_1 is defined as apparent velocity
# of Jupiter along Zodiac in degrees per day
# mean_speed_1 = [ expr { .5 * (velocity_1 - velocity_0 )} ]
proc mean_speed_1 {velocity_1 velocity_0} { expr { .5 * ($velocity_1 - $velocity_0 )} }
# Usage mean_speed_1 1.5 .5 for 1.5 and 0.5 speeds in degrees per day returns 1.
# *******************************
# adding_two_fractions aa/bb + cc/dd =
# ((aa *dd*1.))+(bb*cc*1.))/(bb*dd*1.),
# but must insert 1. factor to return real numbers in TCL math ops
proc adding_two_fractions { aa bb cc dd } { [/ [+ [* $aa $dd 1. ] [* $bb $cc 1. ]] [* $bb $dd 1.] ] }
# suggest maintain spaces in math ops
# Usage adding_two_fractions 1.0 1.0 1.0 1.0 returns 2.0
# Usage adding_two_fractions 1 1 1 1 returns 2.0
# Usage adding_two_fractions 1. 2. 1. 2. returns 1.0
# subtracting_two_fractions aa/bb - cc/dd =
# ((aa *dd*1.))-(bb*cc*1.))/(bb*dd*1.),
# but must insert 1. factor to return real numbers in TCL math ops
proc subtracting_two_fractions { aa bb cc dd } { [/ [- [* $aa $dd 1. ] [* $bb $cc 1. ]] [* $bb $dd 1.] ] }
# subtracting_two_fractions 1. 2. 1. 4. returns 0.25
# subtracting_two_fractions 1. 1. 1. 1. returns 0.0
# subtracting_two_fractions 1 1 1 1 returns 0.0
# multiplying_two_fractions
proc multiplying_two_fractions { aa bb cc dd } { [/ [* $aa $cc 1. ] [* $bb $dd 1. ] ] }
# multiplying_two_fractions 1. 2. 1. 2. returns 0.25
# multiplying_two_fractions 1. 1. 1. 1. returns 1,0
# multiplying_two_fractions 1 1 1 1 returns 1.0
# dividing_two_fractions
# but must insert 1. factor to return real numbers in TCL math ops
proc dividing_two_fractions { aa bb cc dd } { [/ [* $aa $dd 1. ] [* $bb $cc 1. ] ] }
# dividing_two_fractions 1. 1. 1. 2. returns 2.
# dividing_two_fractions 1. 1. 1. 1. returns 1.0
# dividing_two_fractions 1 1 1 1 returns 1.0
# ********************************
proc bodes_law_1 { nn } { return [+ 0.4 [* 0.3 [pow 2 $nn]]] }
# Usage bodes_law_1 1 returns 1.0 Astronomical units for planet Earth
# Usage bodes_law_1 2 returns 0.7 AU for planet Venus
# Usage bodes_law_1 3 returns 1.6 AU for planet Mars
proc bodes_law_2 {} { foreach nn {0 1 2 3 4 5 6 7} { lappend planets [+ 0.4 [* 0.3 [pow 2 $nn]]]};return $planets}
# Usage bodes_law_2 returns list 0.7 1.0 1.6 2.8 5.2 10.0 19.59 38.8
puts " out " # pretty print from autoindent and ased editor
# One Liners Procedures V2
# written on Windows 10 on TCL
# working under TCL version 8.6
# gold on TCL Club , 10Sep2020
package require Tk
package require math::numtheory
package require math::constants
package require math::trig
package require math
namespace path {::tcl::mathop ::tcl::mathfunc math::numtheory math::trig math::constants }
set tclprecision 17
# following dresses up console output to easy eye
console show
console eval {.console config -bg palegreen}
console eval {.console config -font {fixed 20 bold}}
console eval {wm geometry . 40x20}
console eval {wm title . " One Liners Report , screen grab and paste from console 2 to texteditor"}
console eval {. configure -background orange -highlightcolor brown -relief raised -border 30}
# blank table addition
puts "%|table |printed in| tcl wiki format|% "
puts "&| quantity| value| comment, if any|& "
puts "&| testcase number:| |&"
puts "&| value |quantity 1 | |&"
proc pi {} {expr {acos(-1)}}
# proc pi from AMG see below
# ******surface and area calculations ******
proc degtoradiansconst {} { expr {180./ [pi] }}
proc degz {} { expr {180./ [pi] }}
proc degx {aa} { expr { degz *acos($aa)}}
proc inrad {a b c} { expr {(sqrt(($a+$b+$c)*($a+$b-$c)*($a-$b+$c)*($b+$c-$a)))/(2.*($a+$b+$c))}}
proc circlediameter {radius} { expr { 2.* $radius }}
proc circlearea {radius} { expr { [pi] *($radius**2)}}
proc circlecircumference {radius} { expr {2.* [pi] *$radius }}
proc spherediameter {radius} { expr { 2.* $radius }}
proc spherevolume {radius} { expr { (4./3.)* [pi] *($radius**3)}}
proc spheresurface {radius} { expr { 4.* [pi] *($radius**3)}}
proc cubevolume {aa} { expr { 1.*$aa*$aa*$aa }}
proc squarearea {aa} { expr { 1.*$aa*$aa }}
proc ellipsoidvolume {aa bb cc} { expr { 1.*(4./3.)* [pi] *$aa*$bb*$cc }}
proc ellipsearea1 { aa bb } { expr { 1.* [pi] *$aa*$bb }}
proc ellipseperimeterx {aa bb} { set tt [ expr { ($aa*$aa+$bb*$bb)/2.}];return [ expr { 2.*[pi]*sqrt($tt)} ] }
proc spherevolumex {aa } { expr { 1.*(4./3.)* [pi] *$aa*$aa*$aa }}
proc spheroidvolumex {aa cc } { expr { 1.*(4./3.)* [pi] *$aa*$aa*$cc }}
proc torusvolumex {aa bb } { expr {(1./4.) * [pi] * [pi] * ($aa + $bb) * ($aa - $bb)*2.}}
proc torussurfacex {aa bb } { expr { [pi] * [pi] * ($aa*$aa - $bb*$bb)}}
proc conesurfacex {aa rr } { expr { [pi] *$rr*$aa}}
proc cylindersurfacesidex {aa rr } { expr {2.* [pi] *$rr*$aa}}
proc cylinderwholesurfacesidex {aa rr } { expr {2.* [pi] *$rr*$aa +2.* [pi] *$rr*$rr}}
proc cylindervolumesidex {aa rr } { expr { [pi] *$rr*$rr*$aa}}
proc conevolumex {aa rr } { expr { (1./3.)* [pi] *$rr*$rr*$aa}}
proc pyramidvolumex {aa bb cc } { expr {(1./3.)*$aa*$bb*$cc }}
proc rectangularprismvolumex {aa bb cc } { expr { $aa*$bb*$cc }}
proc triangularprismvolumex {aa bb cc } { expr { $aa*$bb*$cc*.5 }}
proc polygonperimeterx {aa bb } { expr { $aa*$bb}}
proc rectangleperimeterx {aa bb } { expr {2.*( $aa+$bb)}}
proc parallelogramperimeterx {aa bb } { expr {2.*( $aa+$bb)}}
proc triangleperimeterx {aa bb cc} { expr { $aa+$bb+$cc }}
proc triangletrapezoidx {aa bb cc} { expr { $aa*($bb+$cc)*(1./2.)}}
# law of cosines, aa bb cc are three sides of right triangle, here ordered
# as aa small side , bb middle side, cc largest side.
# inrad is radius of cirle inscribed in right triangle,
# use sides as inrad aa bb cc
proc anglecosa { aa bb cc } { expr {($bb*$bb+$cc*$cc-$aa*$aa)/(2.*$bb*$cc)}}
proc anglecosb { aa bb cc } { expr {($cc*$cc+$aa*$aa-$bb*$bb)/(2.*$aa*$cc)}}
proc anglecosc { aa bb cc } { expr {($aa*$aa+$bb*$bb-$cc*$cc)/(2.*$aa*$bb)}}
# with examples
# for radius of 1
# circlediameter 1
# circlearea 1
# circlecircumference 1
# spherediameter 1
# spherevolume 1
# spheresurface 1
# inrad 3 4 5
# anglecosa 3 4 5
# anglecosb 3 4 5
# anglecosc 3 4 5
# following include redundant TCL one liner procedures for sqrt of sum of squares
# sqrt of sum of squares and diagonal using expr
proc diagonal_1 {aa bb} { expr { sqrt($aa * $aa + $bb * $bb)}}
# Usage diagonal 1 1 s 1.4142135623730951
# ***** simple interest section *******
# maturity value of loan using TCL 8.6 math ops, 10Sep2020
# similar formula for time in days divide years by 360.
# similar formula for interest rate in percent, divide interest by 100.
# should work with any currency and just use consistent units.
# maintain isolating spaces in TCL math ops
proc maturity_value_loan { principal interest years} { [* $principal [+ 1. [* 1. $interest $years ]]] }
# Usage maturity_value_loan 100. .05 1. returns 105.
proc maturity_value_loan_percent { principal percent_i years} { [* $principal [+ 1. [* 1. [/ $percent_i 100.] $years ]]] }
# Usage maturity_value_loan_percent 100. 5. 1. returns 105.
proc maturity_value_loan_days { principal interest days} { [* $principal [+ 1. [* 1. $interest [/ $days 360. ]]]] }
# Usage maturity_value_loan_days 100. .05 360. returns 105.
# ****** relative error in percent *****************************************
# error in percent is < attested value> over <calculated value> times 100. percent.
# for relative error without percent,
# < attested value> over <calculated value> times 1.0
# for relative error without percent, swap factor 100.0 to 1.0
proc percent_errorx {aa bb} { expr { $aa > $bb ? (($aa*1.)/$bb -1.)*100. : (($bb*1.)/$aa -1.)*100.}}
# Effectively percent_errorx is returning an absolute value of error in percent
# Usage percent_errorx 1.2 1.0 returns 19.99 percent
# Usage percent_errorx 1.0 1.2 returns 19.99 percent
# Usage percent_errorx 1.5 1.0 returns 50.0 percent
proc error_relative {aa bb} { expr { $aa > $bb ? (($aa*1.)/$bb -1.)*1. : (($bb*1.)/$aa -1.)*1.}}
proc error_relative {aa bb} { expr { $aa > $bb ? (($aa*1.)/$bb -1.)*1. : (($bb*1.)/$aa -1.)*1.}}
# Usage error_relative 1.2 1.0 returns 0.199
# Usage error_relative 1.0 1.2 returns 0.199
# Usage error_relative 1.5 1.0 returns 0.50
puts " out "Bounds and Limits on the Collatz_Sequences help define the CS. trajectory and envelope
Recent results have indicated that there are bounds and limits on the Collatz_Sequences that might be useful in TCL expressions.Motta, Oliveira, and Cataban reported that the growth between successive odds is 3/4 . Hence, the reasonable expectation or guess that the sequence will reduce in time. A rigorous result from Krasikov and Lagarias was that the number of N's that inside the region 1 to N that will coalesce or reduce to 1 is greater than expr { $N**.84} . Wulf Rehder reported that the bound on the Collatz_Sequences return to the original entry integer was a constant. The Rehder_limit_collatz_sequences constant is expr { (log(3)/log(2))/(log(3)/log(2)+1.)} returns 0.61314719276545848 or 61.3 percent. The complement or < 1 - Rehder_limit> is 0.3868528072345415 or 38.6 percent . Meaning for long Collatz_Sequences and N>20 is that if one is at the Rehder_limit or return boundary of a long Collatz_Sequence, one can estimate the length of remaining steps of the tail. The Collatz_Sequence has 38.6 percent of tail left. It is curious that some of the TCLLIB Gauss_Legendre estimates for numbers of primes less than N are hovering over the lengths or step numbers of some Collatz_Sequences, N<50. Maybe numerical coincidence, but possibly these Gauss_Legendre procs could be hacked into predicting the length of some Collatz_Sequences. These results are not complete mathematical proofs of the Collatz Conjecture, but believe that the bounds will help characterize the envelope or trajectory of the longer Collatz_Sequences.
Lopsy posted that a number n has rough approximate ~log(n) Collatz steps to reach 1. Some Collatz_Sequences with 2 or more downward sequences and multiple breakpoints may be outliers to this ~log(n) formula. Solution for consecutive numbers with same Collatz length of steps starting at n, X = expr { log(n)* ( log(n))* ( log(log(n)))}, if consecutive numbers are present at number n. Have to check out ~log(n) Collatz steps. There are 7 steps for integer 10 whereasas numberPrimesLegendre 10 returns 7.677. There are 23 steps for integer 100 whereas numberPrimesLegendre 100 returns 27.73.
The Collatz_Sequence for 10 is < 10 5 16 8 4 2 1 > with 7 elements. By inspection, the Collatz_Sequence returns or drops below 10 between elements 3 and 4 or numbers 16 and 8 in the sequence. The Rehder_limit estimates the break point as expr { 7. * .613 } returns 4.291 , rounds to 4. The approximate number of terms or computer steps is 7. Using the Rehder_limit, Rehder_complement, and the expected tail of < 16 8 4 2 1 > , the approximate number of elements is estimated as expr { ( 4.* .613 ) / .386 } returns 6.352, a little off. The Collatz_Sequence for 27 has 112 elements. Sequence for 27 has two breakpoints on elements 96 and 104. At 96, breaks between 46 and 23. The Rehder_limit estimates the break point as expr { 112. * .613 } returns 68.656 , rounds to 69. llength sequence_27_breakpoint returns 96. Sequence for 27 has 16 elements in tail.
# These statements should be pastable into the easy eye console.
# ***** simple interest problems in TCL one liners procedures *****
# find simple interest amount from 3 entries as < principal interest years >
proc simple_interest_amount { principal interest years } { expr { ($principal*1.)*(1.+$years*$interest )}}
# Usage simple_interest_amount 5000. .05 7. returns 6750.0
# find simple interest principal from 3 entries as < amount interest years >
proc simple_interest_principal { amount interest years } { expr { ($amount*1.)/(1.+$years*$interest )}}
# Usage simple_interest_principal 6750.0 .05 7. returns 5000.0
# find simple interest rate from 3 entries as < amount principal years >
proc simple_interest_rate { amount principal years } { expr { ((($amount*1.)/$principal)-1.)/$years }}
# Usage simple_interest_rate 6750.0 5000. 7. returns 0.05
# find years of simple interest from 3 entries as < amount principal interest >
proc simple_interest_years { amount principal interest } { expr { ((($amount*1.)/$principal)-1.)/$interest }}
# Usage simple_interest_years 6750.0 5000. .05 returns 7.0
# ****** compound interest problems in TCL one liners procedures ******
# find compound interest amount from 4 entries as < principal interest years compounding_times_per_year >
# cd is compounding times per year, usually 4 quarters or 12 months
proc compound_interest_amount { principal interest years cd } { expr { ($principal*1.)*((1.+( $interest /$cd))**($years*$cd))}}
# Usage compound_interest_amount 5000 .05 7 12 retuRns 7090.180
# find compound interest principal from 4 entries as < amount interest years cd >
# cd is compounding times per year, usually 4 quarters or 12 months
proc compound_interest_principal { amount interest years cd } { expr { $amount*( 1. +(($interest*1.)/$cd ) )**(-1.*$cd*$years)}}
# Usage compound_interest_principal 7090.180 0.05 7 12 returns 4999.997, rounds to 5000.
# find interest in compound interest from 4 entries as < amount principal years cd >
# cd is compounding times per year, usually 4 quarters or 12 months
proc compound_interest_interest { amount principal years cd } { expr { $cd*((($amount*1.0)/$principal)**(1./($cd*$years))-1.)}}
# Usage compound_interest_interest 7090.180 5000. 7 12 returns 0.049, rounds to 0.05
# find years of compound interest from 4 entries as < amount principal interest cd>
proc compound_interest_years { amount principal interest cd } { expr { (log10 (($amount*1.0)/$principal)) / ($cd*log10(1.+(($interest*1.)/$cd) ) ) }}
# Usage compound_interest_years 7090.180 5000. 0.05 12 returns 6.99, rounds to 7 years
# ******** continuous_compounding ******* based on exponential formulas and natural log.
proc amount_continuous_compounding { principal interest years } { expr { $principal* exp ( $interest*$years*1. ) }}
# Usage amount_continuous_compounding 5000. 0.05 7 returns 7095.3377
proc principal_continuous_compounding { amount interest years } { expr { $amount * exp ( $interest*$years* -1. ) }}
#Usage principal_continuous_compounding 7095.33 0.05 7. returns 4999.994, rounds to 5000.
proc interest_continuous_compounding { amount principal years } { expr { (log ( ($amount*1.) /$principal )) / ($years * log (exp(1.) ) ) }}
# Usage interest_continuous_compounding 7095.33 5000. 7 returns 0.04999, rounds to 0.05
proc years_continuous_compounding { amount principal interest } { expr { (log ( ($amount*1.) /$principal )) / ($interest * log (exp(1.) ) ) }}
# Usage years_continuous_compounding 7095.33 5000. 0.05 returns 6.999, rounds to 7 yearsDraft Wikipedia article on One Liners Programs , TCL Tool Control Language
There is a gold mine of One Liners Programs and content in the Tool Control language TCL 8.6 core distribution, TCL manual pages, and TCLLIB library that can be adapted or recast into brief one liners programs. These one liners programs or procedures can be pasted into the TCL 8.6 console window for quick results, reference the TCL Wiki. Some one liners programs use the return statement, return $value, or return 1 to return the results to the program line. Although many TCL programmers just rely on the last computation being returned by the one liner procedure in the TCL console window. There is some room in the Wiki publications for programming style differences. But it is usually best to put usage, credits, or TCL documentation references for the one liners procedures on separate comment lines. The random procedures make use of the random function and do not return the same answer every time. Dependence on math operator notation, helper procedures, math check examples, and special library functions should be noted in the comment lines.
There are pros and cons to one liner programs in TCL. One may contrast the approach to one liners programs in problem solving versus the traditional procedural approach. There are better routines and methods in faster language constructs in the current TCL core distribution and TCLLIB. Working with recursion, primes, text search, and timing the procedures will quickly show the warts on the one liners programs. To gain speed and shorter computation times, one will generally have to access the TCL core distribution and TCLLIB. Since the TCL interpreter collapses the carriage returns, skips, blank lines, and dead space of traditional written procedures into a single line of machine code, is not every script a one liner program to the parser? As grandfather remarked, the gourmet omelet, beef mulligan stew, and farm buttermilk all go to the same place.
CREDITS ON ONE LINERS
WIKI BOOKS, Programming_Examples pdf WIKI BOOKS, Tcl_Programming_Introduction pdf license https://creativecommons.org/licenses/by-sa/3.0/legalcode creativecommons.org/licenses/by-sa/3.0/ en.wikibooks.org/wiki/Tcl_Programming_Introduction Sample Math Programs, item 2, RS TCLLIB math::mean is quicker by a third over some homebrew code. Additional math functions https://www.quora.com/What-are-the-most-useful-Swiss-army-knife-one-liners-on-Unix-That-is-what-is-your-favorite-one-liner-command-that-handles-a-task-usually-delegated-to-a-much-more-verbose-program-written-in-a-high-level-language http://www.codecodex.com/wiki SOURCE CODE SEARCH ENGINES, INCLUDE TCL???? Google Code Search Koders Krugle Google Code Search Koders Krugle Protecode REFERENCES http://www.codecodex.com/wiki https://www.openhub.net/p?ref=homepage&query=tcl https://en.wikipedia.org/wiki/Portal:Computer_programming https://en.wikipedia.org/wiki/Portal:Free_and_open-source_software https://en.wikipedia.org/wiki/Protecode https://en.wikipedia.org/wiki/List_of_search_engines#Source_code https://blog.robertelder.org/don-libes-expect-unix-automation-tool/
Question from member AV in Russia. So small basic interpreter... Who used small basic interpreters?
A. ## The original tiny basic was distributed in assembler code for the Altair and the 8080 circuit board. Essentially, tiny_basic is a historic legacy of mankind. The original Altair BASIC was about 150 dollars each. Some USA programmers in the 1970s gave away tiny_basic free to break the monopoly. tiny_basic was the first freeware or free software package widely given to the masses (circa 1970). In Russian terms, tiny_basic is the Battleship_Potemkin of computer geeks.
$$$$ The analogy of using tiny_basic to control the large TCL language is like sticking an Apple computer for the human operator in front of a Cray computer. The human mind probably can only understand and use a limited set of instructions, an interface in hardware or TCL? language as a limited set of instructions might be useful. After all, the human mind was designed to chase rabbits.
$$ mostly as a retiree, i am trying to freshen up tcl content on the tcl wiki, adding screenshoots and what meager code i can gin up. I have my limitations, but I am learning.
# conventional expr math operation
# factor 1. forces expression to floating point
proc commission { commission sales } {expr {1.* $commission * $sales}}
# Usage commission .10 100. returns 10.0
# Using math operations notation for speed
proc commission_2 { commission sales } {* 1. $commission $sales }
# Usage commission_2 .1 100 returns 10.0
# *******************************
# commission_rate = commission over sales
set commission_rate {expr {1.*$commission / $sales}}
# conventional expr math operation
proc commission_rate { commission sales } {expr {1.* $commission / $sales}}
# using math operations notation
proc commission_rate_2 { commission sales } [/ [* 1. $commission ] $sales ]
proc commission_rate_2 100. 10.
proc commission_sales_2 { commission sales } {expr {1.* $commission *$sales}} # pretty print from autoindent and ased editor
# Parametric Model Vaporware V2
# written on Windows 10 on TCL
# working under TCL version 8.6
# gold on TCL Club, 4Oct2020
# charting based on rotated ellipse by Gerard Sookahet
# gold added push buttons calculatorand housekeeping
# using dummy calculations for parametric eq. calc.
package require Tk
package require math::numtheory
# added statements for TCLLIB library
package require math::numtheory
package require math::constants
package require math::trig
package require math
namespace path {::tcl::mathop ::tcl::mathfunc math::numtheory math::trig math::constants }
# Tried to keep clean GS code in upper section
set tcl_precision 17
proc pie {} {expr acos(-1)} ;# AMG
# Section EllipseRotate.tcl
# Section proc EllipseRotate Author: Gerard Sookahet
# Date: 09 March 2019
# Version: 0.1
# Description: Simple graphical example of parametric equation of rotated ellipse
#
# xo,yo : center of the ellipse
# angle : rotation angle from 0 to 7 with the scalebar
# a : major radius
# b : minor radius
# t : parameter
bind all <Escape> {exit}
# Section proc Author: Gerard Sookahet
proc EllipseRotate {xo yo a b angle t} {
global side1 side2 side3 side4 side5
global side6 side7 side8
set cosa [expr {cos($angle)}]
set sina [expr {sin($angle)}]
set cost [expr {cos($t)}]
set sint [expr {sin($t)}]
set x [expr {$xo + $a*$cosa*$cost - $b*$sina*$sint}]
set y [expr {$yo + $a*$sina*$cost + $b*$cosa*$sint}]
return [list $x $y]
}
proc EllipsePlot {w xo yo a b pi angle} {
$w delete all
lassign [EllipseRotate $xo $yo $a $b $angle 0] x2 y2
for {set p 0} {$p <= 720} {incr p} {
set t [expr {$pi*$p/360}]
lassign [EllipseRotate $xo $yo $a $b $angle $t] x1 y1
.c create line $x1 $y1 $x2 $y2 -fill blue -width 3
set x2 $x1
set y2 $y1
}
}
# fallback settings
#set width 600
#set height 400
set width 800
set height 500
set pi 3.1415926
set xo [expr {$width/2}]
set yo [expr {$height/2}]
set a 200
set b 100
set angle [expr {$pi/6}]
#pack [canvas .c -width $width -height $height -background black]
#pack [scale .sc -from 0 -to 7 -length 240 -resolution .1 \
-orient horiz -bd 1 -showvalue true -variable angle \
-command {EllipsePlot .c $::xo $::yo $::a $::b $::pi}]
package require Tk
package require math::numtheory
namespace path {::tcl::mathop ::tcl::mathfunc math::numtheory }
set tcl_precision 17
frame .frame -relief flat -bg aquamarine4
pack .frame -side top -fill y -anchor center
set names {{} {parameter 1:} }
lappend names {parameter 2:}
lappend names {parameter 3:}
lappend names {parameter 4:}
lappend names {parameter 5:}
lappend names {parameter 6:}
lappend names {parameter 7:}
lappend names {parameter 8:}
foreach i {1 2 3 4 5 6 7 8} {
label .frame.label$i -text [lindex $names $i] -anchor e
entry .frame.entry$i -width 35 -textvariable side$i
grid .frame.label$i .frame.entry$i -sticky ew -pady 2 -padx 1 }
proc about {} {
set msg "Calculator for Parametric Model Vaporware V2
from TCL ,
# gold on TCL Club, 10Jul2020 "
tk_messageBox -title "About" -message $msg }
proc self_help {} {
set msg "Calculator for Parametric Model Vaporware V2
from TCL ,
# self help listing
# 4 givens follow.
1) parameter 1:
2) parameter 1:
3) parameter 1:
4) parameter 1:
# Recommended procedure is push testcase and fill frame,
# change first three entries etc, push solve,
# and then push report. Report allows copy and paste
# from console to conventional texteditor. For testcases
# testcase number is internal to the calculator and
# will not be printed until the report button is pushed
# for the current result numbers.
# This posting, screenshots, and TCL source code is
# copyrighted under the TCL/TK 8.6 license terms.
# Editorial rights retained under the TCL/TK license terms
# and will be defended as necessary in court.
# gold on TCL Club, 2Oct2020 "
tk_messageBox -title "About" -message $msg }
# uses join, but computer time on some?
proc mean_1 list {expr double([join $list +])/[llength $list]}
# math operators exposed as commands, and the expand operator
# math operators exposed as commands, and the expand operator
proc mean_2 list {expr {[tcl::mathop::+ {*}$list]/double([llength $list])}}
# import the tcl::mathop operators
proc mean_3 list {expr {[+ {*}$list]/double([llength $list])}}
# import the tcl::mathop operators from <Summing a list>
proc table_calc {value} {
# computer drag time sensitive on limit variable
set limit 3
# should apply to at my parametric model
# a list of values (w_list) with cycle for.
# In each step the code must set 3 coefficients (k1,k2,k3)
# copy original format internet query
set w_list [list 0.12 0.14 0.16 0.18 0.20 ];
set k1_list [list {1.080} {1.101} {1.123} {1.144} {1.166}];
set k2_list [list {1.116} {1.213} {1.260} {1.309} {1.360}];
set k3_list [list {1.915} {2.157} {2.402} {2.649} {2.898}];
# gold does not use braces around list elements, left as original
# copy of original format in internet query
# setting table of dummy calculations
# with data supplied in internet query
puts "%|table| | printed in|TCL format |% "
puts "&| session| proc & mean value| elements in list | comment, if any|& "
for { set i 0 } { $i <= $limit } { incr i } {
# may leave redundant or fallback statements in draft program
# set lister { 1 2 4 5 6 7 8 9 10 }
set lister { 0.12 0.14 0.16 0.18 0.20 }
lappend lister [* $i [pie]]
puts "&|$i | mean_1 [ mean_1 $lister ]| $lister | $k1_list | [ mean_1 $k1_list ] |&"
puts "&|$i | mean_2 [ mean_2 $lister ]| $lister | $k2_list | [ mean_2 $k2_list ] |&"
puts "&|$i | mean_3 [ mean_3 $lister ]| $lister | $k2_list | [ mean_3 $k3_list ] |&"
}}
proc calculate { } {
global side1 side2 side3 side4 side5
global side6 side7 side8
global testcase_number
incr testcase_number
set side1 [* $side1 1. ]
set side2 [* $side2 1. ]
set side3 [* $side3 1. ]
set side4 [* $side4 1. ]
set side5 [* $side5 1. ]
set side6 [* $side6 1. ]
set side7 [* $side7 1. ]
set side8 [* $side8 1. ]
set side5 1.
set side6 1.
set side7 1.
set side8 1.
table_calc 1
set w_list [list 0.12 0.14 0.16 0.18 0.20 ]
set velocity_0 $side1
set velocity_1 $side2
set base_line [ expr { abs ( $side4 - $side3 )} ]
set calculation_1 [ expr { .5 * ( $side1 + $side2 ) * 60. } ]
set bisection_1 [ expr { .5 * $calculation_1 } ]
set bisection_velocity_c [ expr { ((($velocity_0)**2 +($velocity_1)**2)/2.)**.5 }]
set bisection_time_c [ expr { $base_line * ( $velocity_0 - $bisection_velocity_c ) / ( $velocity_0 - $velocity_1 ) }]
set side5 $bisection_velocity_c
set side6 $bisection_1
set side7 $bisection_time_c
set side8 $calculation_1
set side1 [* $side1 100. ]
set side2 [* $side2 100. ]
set side3 [* $side3 100. ]
set side4 [* $side4 100. ]
set side5 [* $side5 100. ]
set side6 [* $side6 100. ]
set side7 [* $side7 100. ]
set side8 [* $side8 100. ]
}
proc fillup {aa bb cc dd ee ff gg hh} {
.frame.entry1 insert 0 "$aa"
.frame.entry2 insert 0 "$bb"
.frame.entry3 insert 0 "$cc"
.frame.entry4 insert 0 "$dd"
.frame.entry5 insert 0 "$ee"
.frame.entry6 insert 0 "$ff"
.frame.entry7 insert 0 "$gg"
.frame.entry8 insert 0 "$hh"
}
proc clearx {} {
foreach i {1 2 3 4 5 6 7 8 } {
.frame.entry$i delete 0 end } }
proc reportx {} {
global side1 side2 side3 side4 side5
global side6 side7 side8
global testcase_number
console show;
console eval {.console config -bg palegreen}
console eval {.console config -font {fixed 20 bold}}
console eval {wm geometry . 40x20}
console eval {wm title . " Parametric Model Vaporware V2 Report , screen grab and paste from console 2 to texteditor"}
console eval {. configure -background orange -highlightcolor brown -relief raised -border 30}
puts "%|table $testcase_number|printed in| tcl format|% "
puts "&| quantity| value| comment, if any|& "
puts "&| $testcase_number:|testcase_number | |&"
puts "&| $side1 :|parameter 1: | |&"
puts "&| $side2 :|parameter 2: | |& "
puts "&| $side3 :|parameter 3: | |& "
puts "&| $side4 :|parameter 4: | |&"
puts "&| $side5 :|parameter 5:| | |&"
puts "&| $side6 :|parameter 6:| | |&"
puts "&| $side7 :|parameter 7:| | |&"
puts "&| $side8 :|parameter 8:| | |&"
}
frame .buttons -bg aquamarine4
::ttk::button .calculator -text "Solve" -command { calculate }
::ttk::button .test2 -text "Testcase1" -command {clearx;fillup 1.080 1.101 1.123 1.144 1.116 1.0 1.0 1.0 }
::ttk::button .test3 -text "Testcase2" -command {clearx;fillup 1.116 1.213 1.260 1.309 1.360 1.0 1.0 1.0 }
::ttk::button .test4 -text "Testcase3" -command {clearx;fillup 1.915 2.157 2.402 2.649 2.649 1.0 1.0 1.00 }
::ttk::button .clearallx -text clear -command {clearx }
::ttk::button .about -text about -command {about}
::ttk::button .self_help -text self_help -command {self_help}
::ttk::button .console2 -text report -command { reportx }
::ttk::button .exit -text exit -command {exit}
canvas .c -width $width -height $height -background black
scale .sc -from 0 -to 7 -length 240 -resolution .1 \
-orient horiz -bd 1 -showvalue true -variable angle \
-command {puts " display scale $side1 $side2 $side3 $side4 [pie]"; EllipsePlot .c $side1 $side2 $side3 $side4 [pie]}
pack .c .sc .calculator -in .buttons -side top -padx 10 -pady 5
pack .clearallx .console2 .self_help .about .exit .test4 .test3 .test2 -side left -in .buttons
grid .frame .buttons -sticky ns -pady {0 10}
. configure -background aquamarine4 -highlightcolor brown -relief raised -border 30
wm title . " Parametric Model Vaporware V2"
# gold on TCL Club, 8Jul2020
# This posting, screenshots, and TCL source code is
# copyrighted under the TCL/TK 8.6 license terms.
# Editorial rights retained under the TCL/TK license terms
# and will be defended as necessary in court.
# end of file
Appendix: One Liner Procs for Modeling Planetary Distances using Titius-Bode Law and other power laws
;# for starting the adventure to infinity and beyond.
;# Titius-Bode set < Earth = 1 ... > as number assignment scheme for planets
;# The Asteriod Ceres is included on most number assignment schemes
;# Ceres represents the Asteriod belt between Mars and Jupiter.
;# The dwarf planet Pluto is included on most number assignment schemes.
proc titius_bode_law_1772 {aa } {expr { (4. + 3 * 2**$aa)*.1 } } ;# ;# $nn=l for Earth,2,...
;# Other planet number schemes are for power laws are available here, < Mercury = 1 ...>
;# from Gaussin (1880) and Armellini (1921)
proc gaussin_formula_1880 {nn} {expr {0.2099 * (1.7226 ** $nn)} } ;# $nn=l for Mercury,2,...9
proc armellini_formula_1921 {nn} {expr {0.283 * (1.53 ** $nn)} } ;# $nn=l for Mercury,2,...11
;# very interesting, Nicolini transformed planet number scheme in Titius_Bode
;# to < Mercury = 1 ...>, refer to Nicolini
proc nicolini_formula_1957 {nn} {expr {0.4 + 0.075 * (2. ** $nn)} } ;# $nn=l for Mercury,2,...
proc basano_hughes_formula_1979 {nn} {expr {0.285 * (1.523 ** $nn)} } ;# $nn=l for Mercury, 2,...
;# Sven-Ingmar Ragnarsson, 1994, modeled Jupiter and the outer planets to Uranus, separately.
;# See the Ragnarsson paper, setting these planet assignment numbers is tricky.
;# $nn=0 for Jupiter, 2 = Saturn, 3 = Uranus ....
proc ragnarsson_formula_1979 {nn} {expr {5.203*(((5./2.)**(2./3.))**$nn) )} } ;# $nn=0 for Jupiter, 2 = Saturn,...
proc list_integers { aa bb} { for {set i 1} {$i<=$bb} {incr i} {lappend boo [* 1. $i ] [* $i 1.]};return $boo}
;# usage, list_integers 1 10
;# set answer_list_integers = [list 1.0 1.0 2.0 2.0 3.0 3.0 4.0 4.0 5.0 5.0 6.0 6.0 7.0 7.0 8.0 8.0 9.0 9.0 10.0 10.0 ]
proc list_titius_bode { aa bb} { for {set i 1} {$i<=$bb} {incr i} {lappend boo [* 1. $i ] [expr { (4. + 3. * 2**$i)*.1}]};if {$i > $bb} {return $boo}}
;# Usage list_titius_bode 1 6
;# set answer [ list 1.0 1.0 2.0 1.6 3.0 2.8 4.0 5.2 5.0 10.0 6.0 19.6]
proc list_gaussin_formula { aa bb} { for {set ii 1} {$ii<=$bb} {incr ii} {lappend boo [* 1. $ii ] [expr {0.2099 * (1.7226 ** $ii)} ]};if {$ii > $bb} {return $boo}}
;# Usage list_gaussin_formula 1 6
;# set answer_gaussin [ list 1.0 0.36 2.0 0.62 3.0 1.07 4.0 1.84 5.0 3.18 6.0 5.48 ]
proc list_armellini_formula { aa bb} { for {set ii 1} {$ii<=$bb} {incr ii} {lappend boo [* 1. $ii ] [expr {0.283 * (1.53 ** $ii)}]};if {$ii > $bb} {return $boo}}
;# Usage list_armellini_formula 1 7
;# set answer_armellini [ 1.0 0.43 2.0 0.66 3.0 1.013 4.0 1.55 5.0 2.37 6.0 3.63 7.0 5.55 ]
Console wrapper for solution proc *************************** ***************************
| table 2 | printed in tcl wiki format | ||
|---|---|---|---|
| quantity | value | value | comment, if any |
| 2: | testcase_number | ||
| 13.67 : | initial length | ||
| 1.0 : | iteration : | ||
| 1.0 : | option switch mode, usually 1 , modes = 2, 3, 4: | ||
| 1.0 : | optional constant, nominal 1 :: | ||
| 1. : | experimental decay constant_K1 : | ||
| Note : | experimental constant_k1 not used : | ||
| 54.679999999999993 : | Koch snowflake perimeter from iteration N : | ||
| 80.916607288626935 : | area initial triangle : | ||
| 107.88880971816924 : | area first iteration : | ||
| 107.88880971816926 : | Koch snowflake area from iteration N : | ||
| 129.4665716618031 : | limit to Koch snowflake area from infinite series : | ||
| table 3 | printed in tcl wiki format | ||
| quantity | value | value | comment, if any |
| 3: | testcase_number | ||
| 4.5566666659999999 : | initial length | ||
| 2.0 : | iteration : | ||
| 1.0 : | option switch mode, usually 1 , modes = 2, 3, 4: | ||
| 1.0 : | optional constant, nominal 1 :: | ||
| 1. : | experimental decay constant_K1 : | ||
| Note : | experimental constant_k1 not used : | ||
| 24.302222218666664 : | Koch snowflake perimeter from iteration N : | ||
| 8.9907341405499785 : | area initial triangle : | ||
| 11.987645520733304 : | area first iteration : | ||
| 13.319606134148117 : | Koch snowflake area from iteration N : | ||
| 14.385174624879966 : | limit to Koch snowflake area from infinite series : | ||
| table 4 | printed in tcl wiki format | ||
| quantity | value | value | comment, if any |
| 4: | testcase_number | ||
| 1.5188888 : | initial length | ||
| 3.0 : | iteration : | ||
| 3.0 : | option switch mode, usually 1 , modes = 2, 3, 4: | ||
| 1.0 : | optional constant, nominal 1 :: | ||
| 1. : | experimental decay constant_K1 : | ||
| Note : | experimental constant_k1 not used : | ||
| 10.80098702222222 : | Koch snowflake perimeter from iteration N : | ||
| 0.99897034342930124 : | area initial triangle : | ||
| 1.3319604579057349 : | area first iteration : | ||
| 1.5457318894214702 : | Koch snowflake area from iteration N : | ||
| 1.598352549486882 : | limit to Koch snowflake area from infinite series : | ||
| table 5 | printed in tcl wiki format | ||
| quantity | value | value | comment, if any |
| 5: | testcase_number | ||
| 0.50629629600000003 : | initial length | ||
| 4.0 : | iteration : | ||
| 3.0 : | option switch mode, usually 1 , modes = 2, 3, 4: | ||
| 1.0 : | optional constant, nominal 1 :: | ||
| 1. : | experimental decay constant_K1 : | ||
| Note : | experimental constant_k1 not used : | ||
| 4.8004389546666664 : | Koch snowflake perimeter from iteration N : | ||
| 0.11099671768713089 : | area initial triangle : | ||
| 0.14799562358284118 : | area first iteration : | ||
| 0.17499619688396309 : | Koch snowflake area from iteration N : | ||
| 0.17759474829940941 : | limit to Koch snowflake area from infinite series : | ||
| table 7 | printed in tcl wiki format | ||
| quantity | value | value | comment, if any |
| 7: | testcase_number | ||
| 0.16876543199999999 : | initial length | ||
| 5.0 : | iteration : | ||
| 1.0 : | option switch mode, usually 1 , modes = 2, 3, 4: | ||
| 1.0 : | optional constant, nominal 1 :: | ||
| 1. : | experimental decay constant_K1 : | ||
| Note : | experimental constant_k1 not used : | ||
| 2.1335284242962951 : | Koch snowflake perimeter from iteration N : | ||
| 0.012332968631903429 : | area initial triangle : | ||
| 0.016443958175871239 : | area first iteration : | ||
| 0.019604426284356775 : | Koch snowflake area from iteration N : | ||
| 0.019732749811045485 : | limit to Koch snowflake area from infinite series : |
Under Titius_Bode , Wikipedia page.
Can someone show some sample Cerda calculations on say, Mars and Jupiter. ? What is parameter or function D, not obvious from text. I have programmed the Titius_Bode equation into a Tool Control language TCL program and very interested in programming the Cerda calculations also. Quote: In Tratado de Astronomía, Cerdà obtaines (sp) the planetary distances from the orbital periods by applying Kepler's third law, with an accuracy of 10−3 . Maybe there is a contact interested in working on this item? Thank you.
Taylor series for tangent
;# puts taylor tangent series into pade tangent
;# of rational numbers ratio into horners form
;# num/denum=(1/45*$x**9 - 22*$x**7 + 3003*$x**5 - 105105*$x**3 + 765765*$x)/($x**8 - 308*$x**6 + 21021*$x**4 -
360360*$x**2 + 765765)
;# num=1/45*(((($x**2 - 990)*$x**2 + 135135)*$x**2 - 4729725)*$x**2 + 34459425)*$x
;# denum=((($x**2 - 308)*$x**2 + 21021)*$x**2 - 360360)*$x**2 + 765765
symdiff {(1/45.*$x**9 - 22*$x**7 + 3003*$x**5 - 105105*$x**3 + 765765*$x)} x
((((((9 * pow($x, 8)) * (1 / 45.)) - ((7 * pow($x, 6)) * 22)) + ((5 * pow($x, 4)) * 3003)) - ((3 * pow($x, 2)) * 105105)) + 765765.0)
symdiff {($x**8 - 308*$x**6 + 21021*$x**4 - 360360*$x**2 + 765765)} x
((((8 * pow($x, 7)) - ((6 * pow($x, 5)) * 308)) + ((4 * pow($x, 3)) * 21021)) - ((2 * $x) * 360360))
# Functional math system for integers from RS
# Playing with recursion
# Richard Suchenwirth 2004-10-24
# two functions should be enough to derive all arithmetics
proc func {name argl body} {proc $name $argl [list expr $body]}
proc ' x {incr x}
proc = {m n} {string equal $m $n}
func pred n {[pred2 $n 0]}
func pred2 {n m} {[= [' $m] $n]? $m: [pred2 $n [' $m]]}
proc = {m n} {string equal $m $n}
proc test args {
foreach {case expected} $args {
catch {uplevel 1 $case} res
if {$res != $expected} {error "$case->$res, expected $expected"}
}
}
func + {m n} {[= $n 0]? $m: [+ [' $m] [pred $n]]}
#-- the product
func * {m n} {[= $n 0]? 0: [+ $m [* $m [pred $n]]]}
#-- the difference (defined only for m >= n)
func - {m n} {[= $n 0]? $m: [- [pred $m] [pred $n]]}
#-- the inequality predicate <=
func <= {m n} {[= $m 0]? 1: [= $n 0]? 0: [<= [pred $m] [pred $n]]}
#-- leading to the strict inequality <
func < {m n} {[= $m $n]? 0: [<= $m $n]}
#-- Integer division goes like this:
func / {m n} {[< $m $n]? 0: [' [/ [- $m $n] $n]]}
#-- Integer division remainder (% in expr)
func rem {m n} {[< $m $n]? $m: [rem [- $m $n] $n]}
#-- Divisibility of a number n by a number m
func | {m n} {[= $n 0]? 1: [< $n $m]? 0: [| $m [- $n $m]]}
func prime n {[= $n 0]? 0: [= $n 1]? 0: [prime2 $n 2]}
func prime2 {m n} {[= $m $n]? 1: [| $n $m]? 0: [prime2 $m [' $n]]}
func gcd {m n} {[<= $n $m]? [gcd $n $m]:
[= [rem $n $m] 0]? $m:
[gcd [rem $n $m] $m]}* Pretty Print Version
# pretty print from autoindent and ased editor
# Collatz_Sequences (3*N+1) in Console Example Demo for TCL V2
# Console program example demo
# written on Windows 10 on TCL
# working under TCL version 8.6
# gold on TCL Club , 11sep2021
package require Tk
package require math::numtheory
package require math::constants
package require math::trig
package require math
namespace path {::tcl::mathop ::tcl::mathfunc math::numtheory math::trig math::constants }
set tclprecision 17
# logic tests for even, odd, positive, negative, conditions of positive numbers
# uses logic inside expr , if positive return 1, if not positive return 0
proc isPositive x {return [ expr {$x>0}]}
# Richard Suchenwirth RS idea in Math Sugar
# uses logic inside expr, if negative return 1, if not negative return 0
proc isNegative x { return [ expr {$x<0}]}
# Richard Suchenwirth RS idea from wiki: Math Sugar
# idea by Michael Barth
# No error traps or safety nets here for negative and real numbers.
# conditional proc IsOdd, if N odd, return 1, if N not odd, return 0.
proc IsOdd { N } { return [ expr {$N % 2} ] }
# Usage
IsOdd 5 # returns 1
# conditional proc IsEven, if N even, return 1. If N not even return 0.
proc IsEven { N } { return [ expr { ( $N + 1 ) % 2} ] }
IsEven 4 # returns 1
#
# Results: collatz_sequence
#
# Return the collatz_sequence from positive integer
#
# Arguments:
# number first value is number
# iteration second value is iteration
#
#
# Note: This program can easily generate an endless loop.
# iteration number is a stop or limit to iteration
# By custom, the end of collatz_sequence is 1 or start of repetition
proc collatz_sequence {number iteration} {
# Rewritten by HE on TCL WIKI
# Check parameter
if {!([string is wideinteger $number] && $number > 0)} {
error "Number '$number' is not positive integer!"
}
if {!([string is wideinteger $iteration] && $iteration > 0)} {
error "Iteration '$iteration' is not positiv integer!"
}
# Initialisation
set sequence [list $number]
# Interations
for {set n 0} {$n <= $iteration} {incr n} {
if {$number == 1} {
return $sequence
}
if {$number % 2} {
# Odd
set number [expr {(3 * $number) + 1}]
} else {
set number [expr {$number / 2}]
}
lappend sequence $number
}
# After value reach 1 it is a endless sequence of 4 2 1 4 2 1 ...
# If we reach not 1 during the given ammount of iteration
# we raise an error to signal that number of iterations are to small
# or we reach the case all looking for.
# this error crops with large lists > 15 elements
# error "Number of iteration '$iteration' reached without getting 1!"
}
console show
puts " Console wrapper for solution proc"
puts " ***************************"
puts " ***************************"
puts "collatz_sequence 31 130 collatz_sequence [collatz_sequence 31 130]"
puts "collatz_sequence 11 15 collatz_sequence [collatz_sequence 11 15]"
puts "collatz_sequence 10 15 collatz_sequence [collatz_sequence 10 15]"
puts "collatz_sequence 9 20 collatz_sequence [collatz_sequence 9 20]"
puts "collatz_sequence 8 15 collatz_sequence [collatz_sequence 8 15]"
puts "collatz_sequence 7 20 collatz_sequence [collatz_sequence 7 20]"
puts "collatz_sequence 6 15 collatz_sequence [collatz_sequence 6 15]"
puts "collatz_sequence 5 15 collatz_sequence [collatz_sequence 5 15]"
puts "collatz_sequence 4 15 collatz_sequence [collatz_sequence 4 15]"
puts "collatz_sequence 3 15 collatz_sequence [collatz_sequence 3 15]"
proc table_format_out n {
set sum 0
# initial level
set count 1
puts "%| table| | printed in|TCL format |% "
puts "%| number | iteration |partial Collatz_Sequences |comment, if any|% "
# adapted proc from <RS>
# printout in TCL WIKI format table
for { set i 1 } { $i <= $n } { incr i } {
incr count
puts "&| $count | 120 | [ collatz_sequence $count 120 ]| |&"
incr sum $i
}
return $sum
}
table_format_out 31
# following dresses up console output to easy eye
# end of working deck
# add cosmetics below to bottom of file
console eval {.console config -bg palegreen}
console eval {.console config -font {fixed 20 bold}}
console eval {wm geometry . 40x20}
console eval {wm title . " Report for Collatz_Sequences (3*N+1) Calculator V2 "}
console eval {. configure -background orange -highlightcolor brown -relief raised -border 30} Pseudocode and Equations Section
#pseudocode can be developed from rules of thumb.
#pseudocode: some problems can be solved by proportions (rule of three), to some order of magnitude
#pseudocode: enter quantity1, quantity2, quantity3 and expected output (quantity4) for testcases.
#pseudocode: enter time in years, number of remaining items
#pseudocode: output fraction of (remaining items) over (items at time zero)
#pseudocode: ouput remaining items as fraction or percent
#pseudocode: output fraction of (quantity4 ) over ( quantity1 at time zero)
#pseudocode: output fraction of (quantity2) * (quantity3 ) over (quantity1 at time zero)
#pseudocode: outputs should be in compatible units.
#pseudocode: rules of thumb can be 3 to 15 percent off, partly since g..in g..out.
#pseudocode: need test cases > small,medium, giant
#pseudocode: need testcases within range of expected operation.
#pseudocode: are there any cases too small or large to be solved?
#; Terence Tao realized that the Collatz conjecture was similar to partial differential equations.
#; The Tao starting sample weighs toward numbers that
#; have a remainder of 1 after being divided by 3,
#; and away from numbers that have a remainder of 2 after being divided by 3.
#; TCL pseudocode
#; remove all numbers divisible by 3 on a list of integers,
#; find all numbers that have a remainder of 1, when divided by 3.PYK 2020-10-13: Hi gold, thank you for the cool pages you've contributed to this wiki. Your recent edit to upvar sugar was reverted by stevel, probably because it was so broad. My opinion: The concern is that if such broad reference sections proliferate, they lose the value they might have had. There is a natural hierarchy to content on the wiki. The page above upvar sugar is probably something like little language. A link to math sugar, for example, is a sibling to upvar sugar, so probably belongs on a higher page, and not on the upvar sugar page. For navigational purposes it's good enough to be able to browse through a "path" of links to some indirectly-related content, and to constrain the "reference" section only to directly-related pages, i.e. pages that might be considered siblings, children, or parents.
PYK 2020-10-21: In my recent edit to Playing Recursion V2 >> demo examples for one liner programs I removed the copyright notice. The entire content of this wiki is intended to be in th public domain, and thus copyright notices on individual pages are unneeded and could cause confusion. See Who owns the content on this Wiki.
gold 2020-10-20. How about me just loading the pix and charts alone at the bottom of these older works by other authors? That should not spoil the looks and "optics" of the older author pages. Since my moniker is on the pix, if readers want more info, refs, and the generating code, they may contact me. I do not have an ax to grind on copyright, other than no liability to me and TCL Wiki. I have some brain fog late at night, page was overwritten somehow. I have reloaded your edit 102 from the history, with omissions per request.
gold 2021-5-8. Removing copyright notices on <gold> authored pages as spare time allows. I do not have an ax to grind on copyright, other than no liability to me and TCL Wiki. The 2007 paper of David McFarland provided an excellent history of the quarter square multiplication algorithm in both the ancient and modern eras. The college institutes, textbooks, and computer companies in the USA that previously used the Babylonian mathematical ideas without credit may be glad to know that the Babylonian copyrights and patents expired about 4000 years ago.
Hidden Comments Section
If urgent matter, leave comment out in plain sight, here at bottom of page. As I am more likely to see it. If the issue is resolved, I may sweep under rug later.
Please include your wiki MONIKER and date in your comment with the same courtesy that I will give you. Thanks, gold 12Dec2018
PYK 2020-10-13: Hi gold, thank you for the cool pages you've contributed to this wiki. Your recent edit to upvar sugar was reverted by stevel, probably because it was so broad. My opinion: The concern is that if such broad reference sections proliferate, they lose the value they might have had. There is a natural hierarchy to content on the wiki. The page above upvar sugar is probably something like little language. A link to math sugar, for example, is a sibling to upvar sugar, so probably belongs on a higher page, and not on the upvar sugar page. For navigational purposes it's good enough to be able to browse through a "path" of links to some indirectly-related content, and to constrain the "reference" section only to directly-related pages, i.e. pages that might be considered siblings, children, or parents.
PYK 2020-10-21: In my recent edit to Playing Recursion V2 >> demo examples for one liner programs I removed the copyright notice. The entire content of this wiki is intended to be in the public domain, and thus copyright notices on individual pages are unneeded and could cause confusion. See Who owns the content on this Wiki.
gold 2020-10-20. How about me just loading the pix and charts alone at the bottom of these older works by other authors? That should not spoil the looks and "optics" of the older author pages. Since my moniker is on the pix, if readers want more info, refs, and the generating code, they may contact me. I do not have an ax to grind on copyright, other than no liability to me and TCL Wiki. I have some brain fog late at night, page was overwritten somehow. I have reloaded your edit 102 from the history, with omissions per request.
gold 2021-5-8. Removing copyright notices on <gold> authored pages as spare time allows. I do not have an ax to grind on copyright, other than no liability to me and TCL Wiki. The 2007 paper of David McFarland provided an excellent history of the quarter square multiplication algorithm in both the ancient and modern eras. The college institutes, textbooks, and computer companies in the USA that previously used the Babylonian mathematical ideas without credit may be glad to know that the Babylonian copyrights and patents expired about 4000 years ago.
| Category Numerical Analysis | Category Toys | Category Calculator | Category Mathematics | Category Example | Toys and Games | Category Games | Category Application | Category GUI |